激活函数总结(十七):激活函数补充(PELU、Phish)
激活函数总结(十七):激活函数补充
- 1 引言
- 2 激活函数
- 2.1 Parametric Exponential Linear Unit(PELU)激活函数
- 2.2 Phish激活函数
- 3. 总结
1 引言
在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、Leaky ReLU、PReLU、Swish、ELU、SELU、GELU、Softmax、Softplus、Mish、Maxout、HardSigmoid、HardTanh、Hardswish、HardShrink、SoftShrink、TanhShrink、RReLU、CELU、ReLU6、GLU、SwiGLU、GTU、Bilinear、ReGLU、GEGLU、Softmin、Softmax2d、Logsoftmax、Identity、LogSigmoid、Bent Identity、Absolute、Bipolar、Bipolar Sigmoid、Sinusoid、Cosine、Arcsinh、Arccosh、Arctanh、LeCun Tanh、TanhExp、Gaussian 、GCU、ASU、SQU、NCU、DSU、SSU、SReLU、BReLU)。在这篇文章中,会接着上文提到的众多激活函数继续进行介绍,给大家带来更多不常见的激活函数的介绍。这里放一张激活函数的机理图:

2 激活函数
2.1 Parametric Exponential Linear Unit(PELU)激活函数
Parametric Exponential Linear Unit(PELU)是一种 Exponential Linear Unit(ELU)的变种激活函数,它引入了可学习的参数,允许网络自适应地调整激活函数的形状。其数学表达式为和数学图像分别如下所示:
f a , b ( x ) = { a ( e x b − 1 ) , for x < 0 a b x , for 0 ≤ x f_{a,b}(x)= \begin{cases} a(e^{\frac{x}{b}} - 1), & \text{for } x < 0 \\ \frac{a}{b}x, & \text{for } 0 \leq x \\ \end{cases} fa,b(x)={a(ebx−1),bax,for x<0for 0≤x
优点:
- 非线性特性: PELU 引入了
非线性特性,使得网络能够更好地适应数据中的复杂模式。 - 可学习参数: PELU 允许
学习参数,这意味着网络可以根据数据和任务需求自适应地调整激活函数的形状。 - 避免梯度消失: 对于负的输入,PELU 引入了
指数项,这有助于在一些情况下避免梯度消失问题。 - 平滑性: PELU 在负的输入范围内是
平滑的,这有助于梯度计算和反向传播的稳定性。
缺点:
- 计算复杂性: 相对于一些简单的激活函数(如 ReLU)而言,PELU 的
计算复杂性较高,尤其是因为它涉及指数计算。 - 参数选择: 学习参数需要额外的
调整和调优,这可能需要更多的实验。
需要注意的是,PELU 激活函数可以作为一种探索性尝试,具有自适应形状的特点可能对某些问题有益。然而,在使用之前,您应该仔细考虑其优点和缺点,并在实验中评估其在具体任务和数据上的性能。
2.2 Phish激活函数
论文链接:Phish: A Novel Hyper-Optimizable Activation Function
Phish 是一种新颖的激活函数。它是一个GELU和TanH的复合函数,其数学表达式为和数学图像分别如下所示:
f ( x ) = x ∗ T a n H ( G E L U ( x ) ) f(x) = x*TanH(GELU(x)) f(x)=x∗TanH(GELU(x))
优点:
- 连续可微:在观察到的域上的
微分图中没有明显的不连续性 - 新颖:该激活函数是
2022年提出的 - 有效性:实验结果表明Phish激活函数具有
较好的效果。
缺点:
- 缺乏验证:虽然论文中说明具有较好效果,但是未经过
广泛验证
虽然该算法在论文中呈现出较好的效果,但是当前仍未经过有效验证。。。。
3. 总结
到此,使用 激活函数总结(十七) 已经介绍完毕了!!! 如果有什么疑问欢迎在评论区提出,对于共性问题可能会后续添加到文章介绍中。如果存在没有提及的激活函数也可以在评论区提出,后续会对其进行添加!!!!
如果觉得这篇文章对你有用,记得点赞、收藏并分享给你的小伙伴们哦😄。
相关文章:

激活函数总结(十七):激活函数补充(PELU、Phish)
激活函数总结(十七):激活函数补充 1 引言2 激活函数2.1 Parametric Exponential Linear Unit(PELU)激活函数2.2 Phish激活函数 3. 总结 1 引言 在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、…...
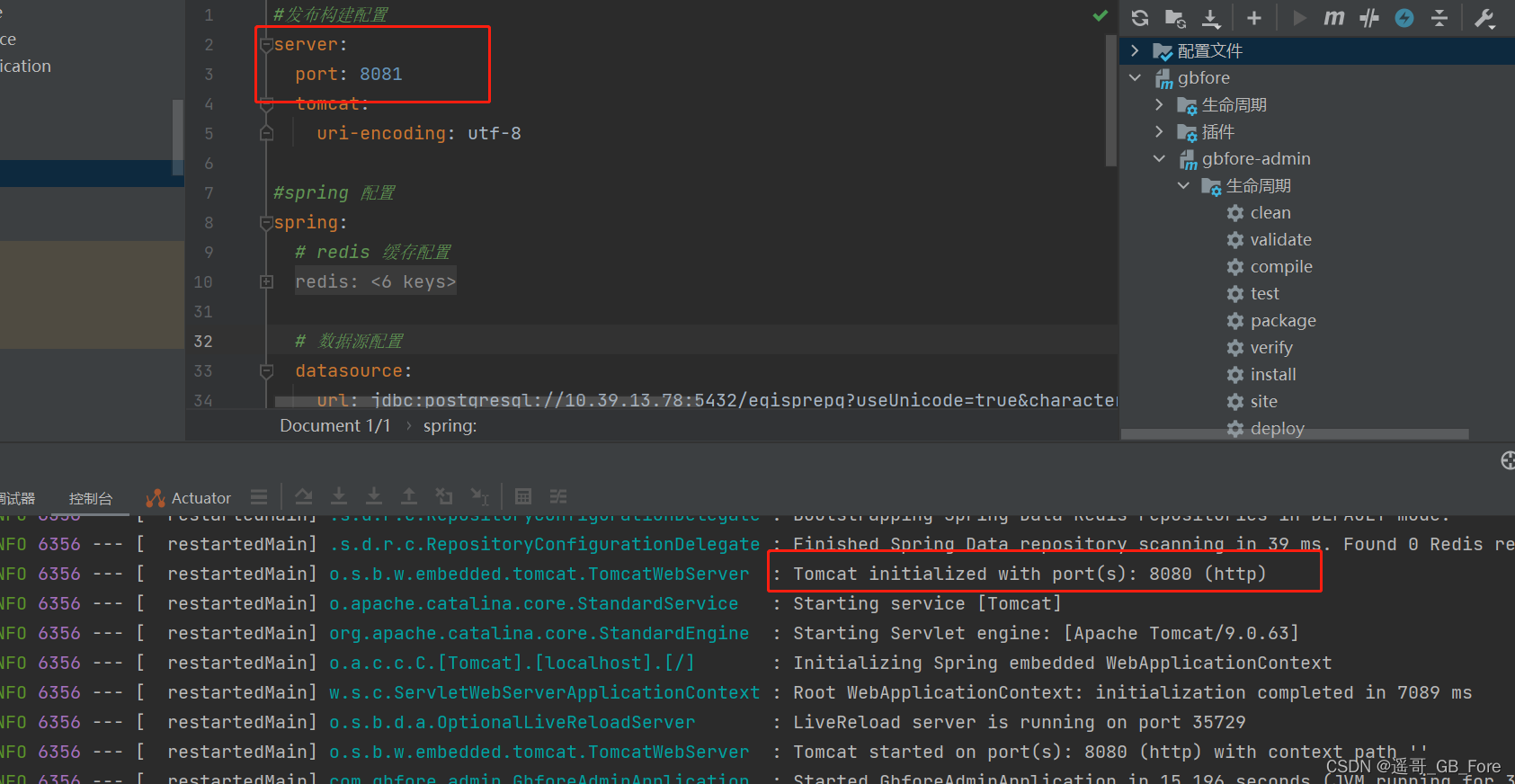
[bug日志]springboot多模块启动,在yml配置启动端口8081,但还是启动了8080
【问题描述】 配置的启动端口是8081,实际启动端口是8080 【解决方法】 1.检查application.yml的配置是否有错误(配置项中,显示白色就错,橙色无措) 2.检查pom.xml的打包方式配置项配置,主pom.xml中的配置项一般为:&l…...

【每日易题】七夕限定——单身狗问题以及进阶问题位运算法的深入探讨
君兮_的个人主页 勤时当勉励 岁月不待人 C/C 游戏开发 Hello,米娜桑们,这里是君兮_,在写这篇博客的前一天是七夕,也是中国传统的“情人节”,不知道各位脱单了吗?碰巧最近刷题时遇到了经典的单身狗问题想带大家深入探…...

消息队列前世今生 字节跳动 Kafka #创作活动
消息队列前世今生 1.1 案例一: 系统崩溃 首先大家跟着我想象一下下面的这个的场景, 看到新出的游戏机,太贵了买不起,这个时候你突然想到,今天抖音直播搞活动,打开抖音搜索,找到直播间以后&am…...

『SEQ日志』在 .NET中快速集成轻量级的分布式日志平台
📣读完这篇文章里你能收获到 如何在Docker中部署 SEQ:介绍了如何创建和运行 SEQ 容器,给出了详细的执行操作如何使用 NLog 接入 .NET Core 应用程序的日志:详细介绍了 NLog 和 NLog.Seq 来配置和记录日志的步骤日志记录示例&…...
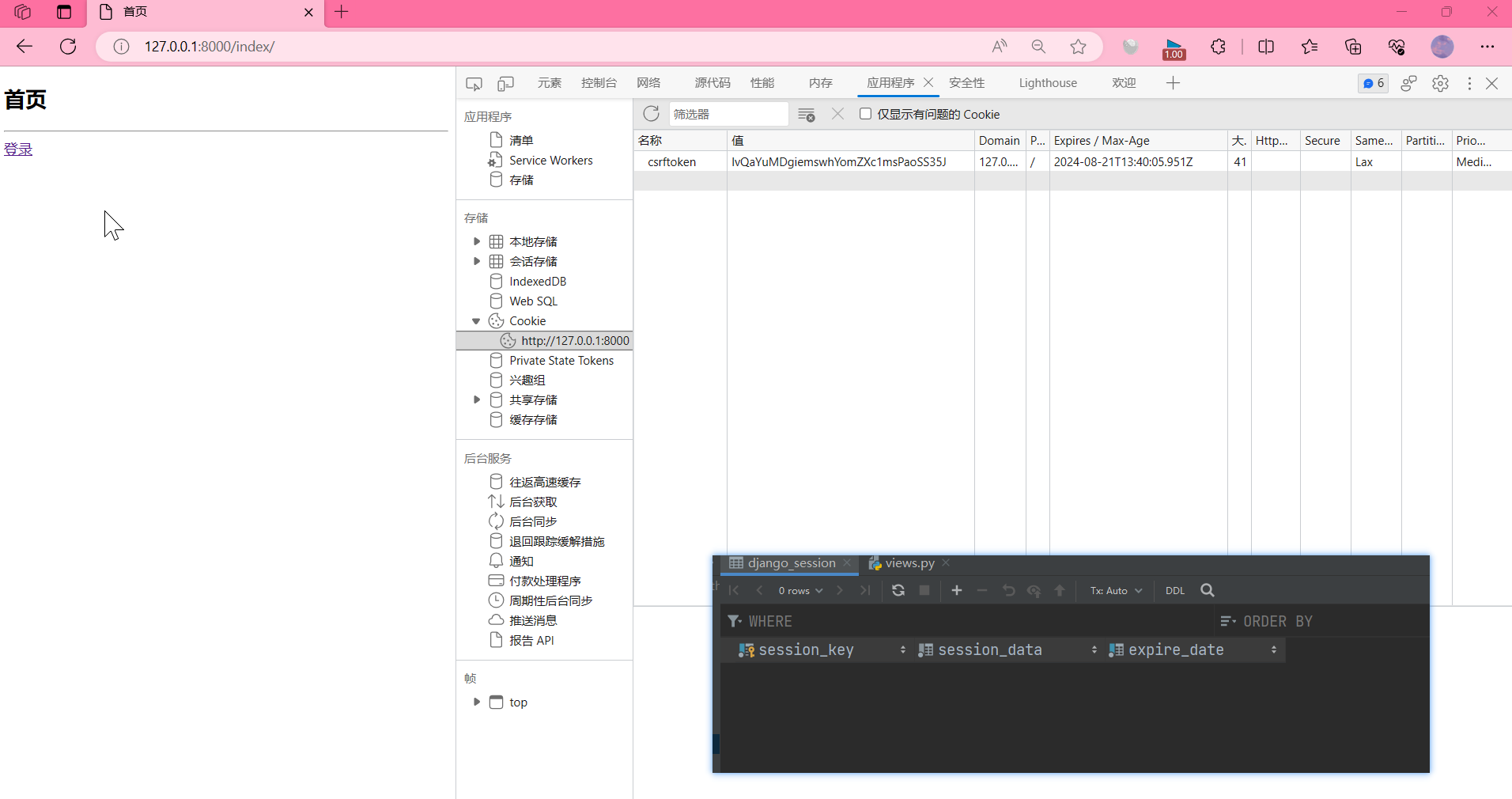
Django会话技术
文章目录 Cookie实践运行结果 CSRF防止CSRF Session实践 Cookie 理论上,一个用户的所有请求燥作都应该属于同一个会话,而另一个用户的所有请求操作则应该属于另一个会话,二者不能混淆,而web应用程序是使用HTTP协议传输数据的。HTT…...

Tree of Thoughts: Deliberate Problem Solving with Large Language Models
本文是LLM系列的文章,针对《Tree of Thoughts: Deliberate Problem Solving with Large Language Models》的翻译。 思维树:用大模型进行深思熟虑的问题解决 摘要1 引言2 背景3 思维树:用LM进行深思熟虑的问题解决4 实验5 相关工作6 讨论 摘…...
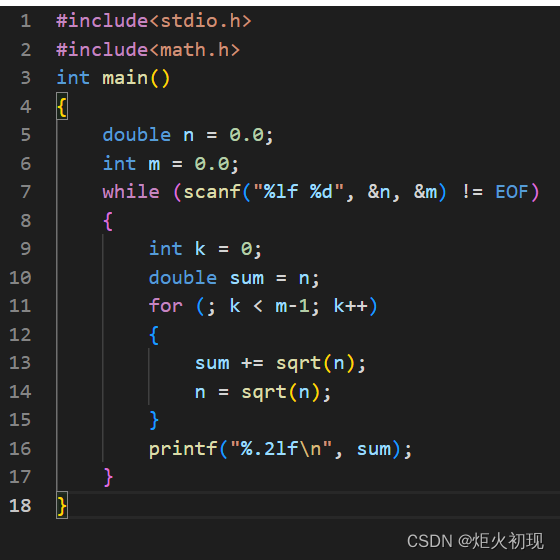
C语言刷题(13)
第一题 第二题 第三题 第四题 第五题 第六题 第七题 注意 1.nsqrt(n),sqrt本身不会将n开根 2.初始化已经令sumn了,故相加的个数为m-1次...
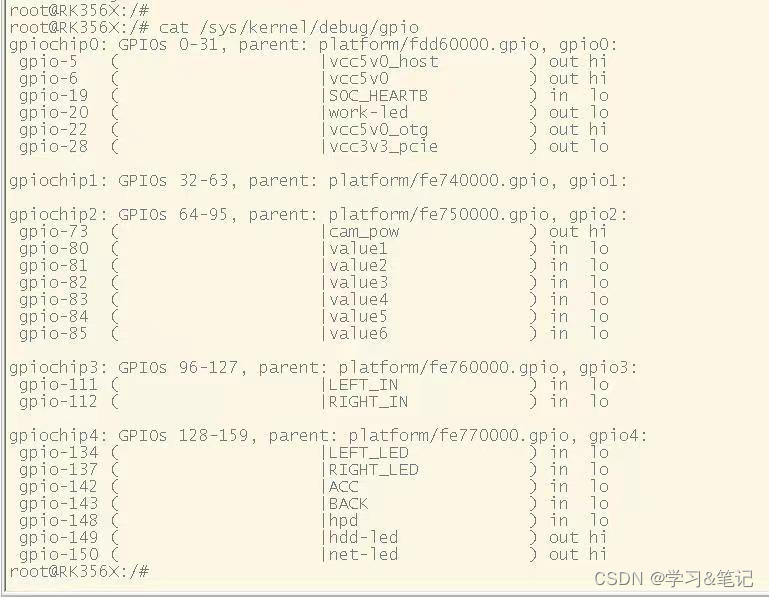
RK3568 uart串口
一.简介 串口全称叫做串行接口,通常也叫做 COM 接口,串行接口指的是数据一个一个的顺序传 输,通信线路简单。使用两条线即可实现双向通信,一条用于发送,一条用于接收。串口通信 距离远,但是速度相对会低&a…...

企业数字化转型中,VR数字展厅能有哪些体验?
在数字化转型的浪潮下,企业纷纷开始注重数字展厅的开展,VR虚拟展厅结合VR全景技术,可以创造出许多有趣的玩法和体验,无论是虚拟参观、互动体验还是VR云会议对接,都为企业客户带来了全新的感知方式。 同传统展厅相比&am…...

关于cesium中tif文件处理加载在三维地图中得方式
项目场景: 在Gis项目关于tif影像数据是不能直接在地图上面加载,只能通过后端进行处理,或者前端进行处理之后才能叠加到地图上面! 处理方式 1.安装geotiff插件 npm install geotiff -g2.利用插件处理tif文件 import GeoTIFF, { fromBlob, fromUrl, fromArrayBuff…...

JAVA结合AE(Adobe After Effects)AE模板文件解析生成视频实现类似于逗拍(视频DIY)的核心功能
最近看抖音上有很多各种视频表白生成的直播而且直播间人很多,于是就思考如何实现的视频内的文字图片内容替换的呢 ,答案需要用到类似与逗拍一样的视频DIY的功能,苦于我是java,百度了半天没有办法和思路,总不能为了一个…...
美容行业如何快速搭建自己的预约小程序?
现在,搭建一个专属于美容行业的预约小程序不再是只有程序员才能做到的事情了。有了一些小程序制作平台的存在,任何人都可以轻松地制作出自己的小程序。下面,我将揭秘一个快速搭建专属美容行业预约小程序的秘诀。 首先,登录小程序制…...

如何使用CSS实现一个水平居中和垂直居中的布局?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 水平居中布局⭐ 垂直居中布局⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴趣…...

关于css 的选择器和 css变量
css 选择器 常用的选择器 1. 后代选择器:也就是我们常见的空格选择器,选择的对象为该元素下的所有子元素 。例如,选择所有 元素下的 元素 div p{font-size:14px}2. 子元素选择器 ‘>’ 选择某元素下的直接子元素。例如,选择所…...
——编程语言的选择)
大数据技术概述(三)——编程语言的选择
文章目录 1.6编程语言的选择1.6.1java和Scala1.6.2Python1.6.3SQL 1.6编程语言的选择 大数据编程一般会使用Java、Scala和python等编程语言,Flink目前也支持上述3种语言。 1.6.1java和Scala Java支持多线程,其生态圈中可用的第三方库众多。Java虚拟机…...
Flutter对象状态动态监听Watcher
场景:当一个表单需要在表单全部或者特定项赋值后才会让提交按钮可点击。 1.普通实现方式: ///场景:检查[test11][test12][test13]均不为空时做一些事情,例如提交按钮变成可点击String? test11;String? test12;int? test13;///当…...

期权分仓开户资金是否安全?具体保障措施有哪些?
网上关于期权分仓系统的真假一直都没有定论,两方人的争论也让很多没有接触过期权分仓系统的人摸不着头脑,那么期权分仓靠谱吗?资金在里面安全吗?下文为大家科普期权分仓开户资金是否安全?具体保障措施有哪些? 一、期权…...

Unity Mac踩坑日记
1、读取外部文件夹使用IO,读取StreamingAsset或者Unity定义文件夹或者服务器文件使用www或者UnityRequest 2、mac下使用www 需要添加前缀:"file://" 3、Mac下的Rider很好用,断点调试也很方便 4、改变文件编码格式,使…...
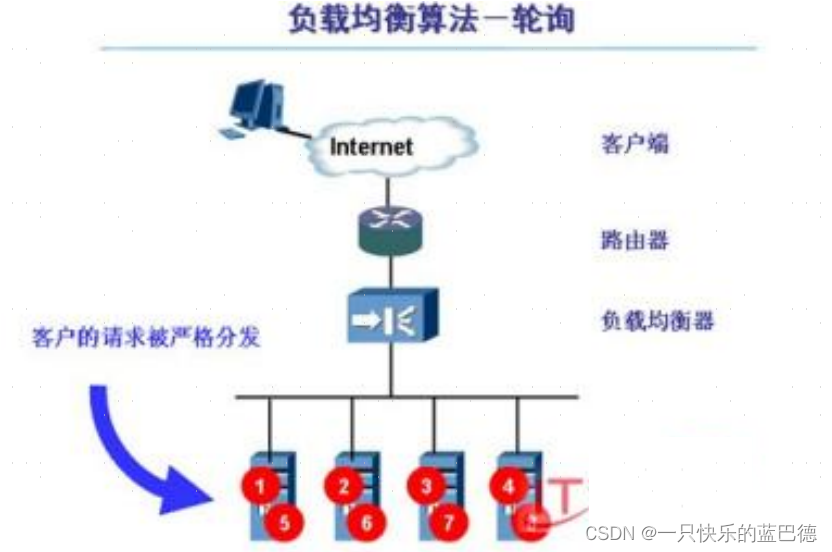
什么是负载均衡
前提概述 关于负载均衡,我会从四个方面去说 1. 负载均衡产生的背景 2. 负载均衡的实现技术 3. 负载均衡的作用范围 4. 负载均衡的常用算法 负载均衡的诞生背景 在互联网发展早期,由于用户量较少、业务需求也比较简单。对于软件应用,我们只需要…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
