高等数学:线性代数-第三章
文章目录
- 第3章 矩阵的初等变换与线性方程组
- 3.1 矩阵的初等变换
- 3.2 矩阵的秩
- 3.3 方程组的解
第3章 矩阵的初等变换与线性方程组
3.1 矩阵的初等变换
矩阵的初等变换 下面三种变换称为矩阵的初等变换
对换两行(列),记作 r i ↔ r j ( c i ↔ c j ) r_{i} \leftrightarrow r_{j} (c_{i} \leftrightarrow c_{j}) ri↔rj(ci↔cj)
以数 k ≠ 0 k \ne 0 k=0 乘某一行(列)中的所有元,记作 r i × k ( c i × k ) r_{i} \times k ( c_{i} \times k ) ri×k(ci×k)
把某一行(列)所有元的 k 倍加到另一行(列)对应的元上去,记作 r i + k r i ( c i + k c i ) r_{i} + kr_{i} ( c_{i} + kc_{i} ) ri+kri(ci+kci)
矩阵等价 如果矩阵 A \bm{A} A 经过优有限次初等变换变成矩阵 B \bm{B} B ,就称矩阵 A \bm{A} A 与矩阵 B \bm{B} B 等价,记作 A ∼ B \bm{A} \sim \bm{B} A∼B .
矩阵等价满足:
A ∼ A \bm{A} \sim \bm{A} A∼A
若
A ∼ B \bm{A} \sim \bm{B} A∼B
则
B ∼ A \bm{B} \sim \bm{A} B∼A
若
A ∼ B \bm{A} \sim \bm{B} A∼B
B ∼ C \bm{B} \sim \bm{C} B∼C
则
A ∼ C \bm{A} \sim \bm{C} A∼C
定理 设 A \bm{A} A与 B \bm{B} B 为 m × n m \times n m×n矩阵,那么
A ∼ r B \bm{A} \overset{r}{\sim} \bm{B} A∼rB的充分必要条件是 ∃ P = ( p i j ) m × m , ∣ P ∣ ≠ 0 s . t . P A = B \exists \bm{P} = (p_{ij})_{m \times m},~|\bm{P}| \ne 0 ~~ s.t.~\bm{P}\bm{A}=\bm{B} ∃P=(pij)m×m, ∣P∣=0 s.t. PA=B
A ∼ r B \bm{A} \overset{r}{\sim} \bm{B} A∼rB的充分必要条件是 ∃ Q = ( q i j ) n × n , ∣ Q ∣ ≠ 0 s . t . A Q = B \exists \bm{Q} = (q_{ij})_{n \times n},~|\bm{Q}| \ne 0 ~~ s.t.~\bm{A}\bm{Q}=\bm{B} ∃Q=(qij)n×n, ∣Q∣=0 s.t. AQ=B
A ∼ B \bm{A} \sim \bm{B} A∼B的充分必要条件是 ∃ P = ( p i j ) m × m , Q = ( q i j ) n × n , ∣ P ∣ ≠ 0 , ∣ Q ∣ ≠ 0 s . t . P A Q = B \exists \bm{P} = (p_{ij})_{m \times m},~ \bm{Q} = (q_{ij})_{n \times n},~ |\bm{P}| \ne 0,~ |\bm{Q}| \ne 0 ~~ s.t.~ \bm{PAQ}=\bm{B} ∃P=(pij)m×m, Q=(qij)n×n, ∣P∣=0, ∣Q∣=0 s.t. PAQ=B
3.2 矩阵的秩
子式 在 m × n m \times n m×n矩阵 A \bm{A} A中,任取 k 行 k 列,位于这些行列交叉处的 k 2 k^{2} k2 个元素,不改变它们在 A \bm A A中所处的位置次序而得的 k 阶行列式,称为矩阵 A \bm A A的 k 阶子式。
秩 若矩阵 A \bm A A中存在一个不为零的 r 阶子式,且所有 r+1 阶子式全为零,那么数 r 称为矩阵 A \bm A A 的秩,记作 R ( A ) R(\bm A) R(A). 规定零矩阵的秩为 0 .
矩阵的秩有以下性质:
0 ≤ R ( ( a i j ) m × n ) ≤ min { m , n } R ( ( A ) T ) = R ( A ) ∣ ( a i j ) n × n ∣ = 0 , R ( ( a i j ) n × n ) < n 0\leq R((a_{ij})_{m \times n})\leq\min\{m,n\} R((\bm A)^\mathrm T) = R(\bm A) |(a_{ij})_{n \times n}|=0,~ R((a_{ij})_{n \times n})<n 0≤R((aij)m×n)≤min{m,n}R((A)T)=R(A)∣(aij)n×n∣=0, R((aij)n×n)<n
若 A ∼ B \bm A\sim\bm B A∼B ,则 R ( A ) = R ( B ) max { R ( A ) , R ( B ) } ≤ R ( A , B ) ≤ R ( A ) + R ( B ) R(\bm A)=R(\bm B) \max\{R(\bm A),R(\bm B)\}\leq R(\bm A,\bm B)\leq R(\bm A)+R(\bm B) R(A)=R(B)max{R(A),R(B)}≤R(A,B)≤R(A)+R(B)
R ( A + B ) ≤ R ( A ) + R ( B ) R(\bm A+\bm B)\leq R(\bm A)+R(\bm B) R(A+B)≤R(A)+R(B)
R ( A B ) ≤ min { R ( A ) , R ( B ) } R(\bm{AB})\leq\min\{R(\bm A),R(\bm B)\} R(AB)≤min{R(A),R(B)}
若 A m × n B n × l = O \bm{A}_{m \times n}\bm{B}_{n \times l}=\bm O Am×nBn×l=O,则 R ( A ) + R ( B ) ≤ n R(\bm A)+R(\bm B) \leq n R(A)+R(B)≤n
3.3 方程组的解
n \bm n n 元齐次线性方程组解的判定 n 元齐次线性方程组 A x = 0 \bm{Ax}=\bm{0} Ax=0 解的情况如下:
有非零解的充分必要条件是 R ( A ) < n R(\bm A)<n R(A)<n,即 ∣ A ∣ = 0 | \bm A | = 0 ∣A∣=0
只有零解的充分必要条件是 R ( A ) = n R(\bm A)=n R(A)=n ,即 ∣ A ∣ ≠ 0 |\bm A|\ne0 ∣A∣=0
n \bm n n 元非齐次线性方程组解的判定 n 元非齐次线性方程组 A x = b \bm{Ax}=\bm{b} Ax=b 解的情况如下:
无解的充分必要条件是 R ( A ) < R ( A , b ) R(\bm A)<R(\bm A,\bm b) R(A)<R(A,b)
有解的充分必要条件是 R ( A ) = R ( A , b ) R(\bm A)=R(\bm A,\bm b) R(A)=R(A,b) ,其中
有惟一解的充分必要条件是 R ( A ) = R ( A , b ) = n R(\bm A)=R(\bm A,\bm b)=n R(A)=R(A,b)=n
有无穷多解的充分必要条件是 R ( A ) = R ( A , b ) < n R(\bm A)=R(\bm A,\bm b)<n R(A)=R(A,b)<n
矩阵方程解的判定 矩阵方程 A X = B \bm{AX}=\bm{B} AX=B 解的情况如下:
无解的充分必要条件是 R ( A ) < R ( A , B ) R(\bm A)<R(\bm A,\bm B) R(A)<R(A,B)
有解的充分必要条件是 R ( A ) = R ( A , B ) R(\bm A)=R(\bm A,\bm B) R(A)=R(A,B)
相关文章:

高等数学:线性代数-第三章
文章目录 第3章 矩阵的初等变换与线性方程组3.1 矩阵的初等变换3.2 矩阵的秩3.3 方程组的解 第3章 矩阵的初等变换与线性方程组 3.1 矩阵的初等变换 矩阵的初等变换 下面三种变换称为矩阵的初等变换 对换两行(列),记作 r i ↔ r j ( c i …...

深入理解 SQL 注入攻击原理与防御措施
系列文章目录 文章目录 系列文章目录前言一、SQL 注入的原理二、防御 SQL 注入攻击的措施1. 使用参数化查询2.输入验证与过滤3.最小权限原则4.不要动态拼接 SQL5.ORM 框架6.转义特殊字符三、实例演示总结前言 SQL 注入是一种常见的网络攻击方式,攻击者通过在输入框等用户交互…...
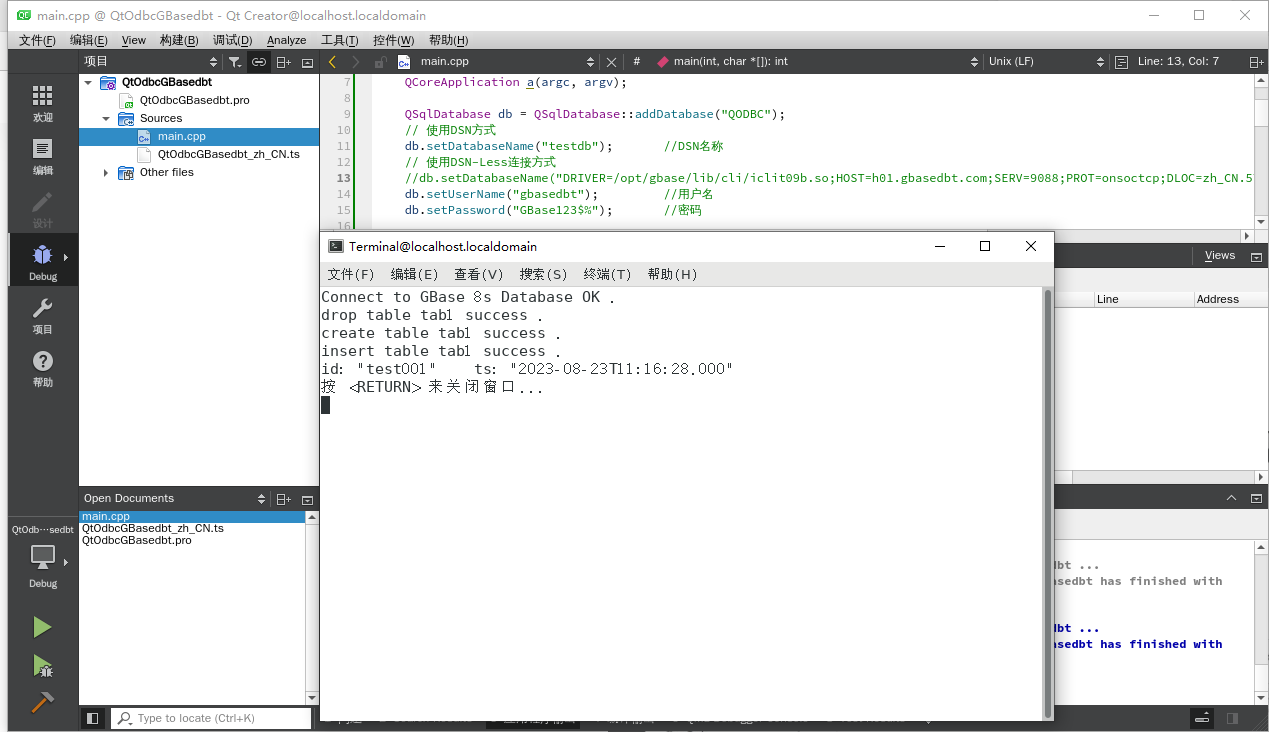
QT5.12.12通过ODBC连接到GBase 8s数据库(CentOS)
本示例使用的环境如下: 硬件平台:x86_64(amd64)操作系统:CentOS 7.8 2003数据库版本(含CSDK):GBase 8s V8.8 3.0.0_1 为什么使用QT 5.12.10?该版本包含QODBC。 1&#…...
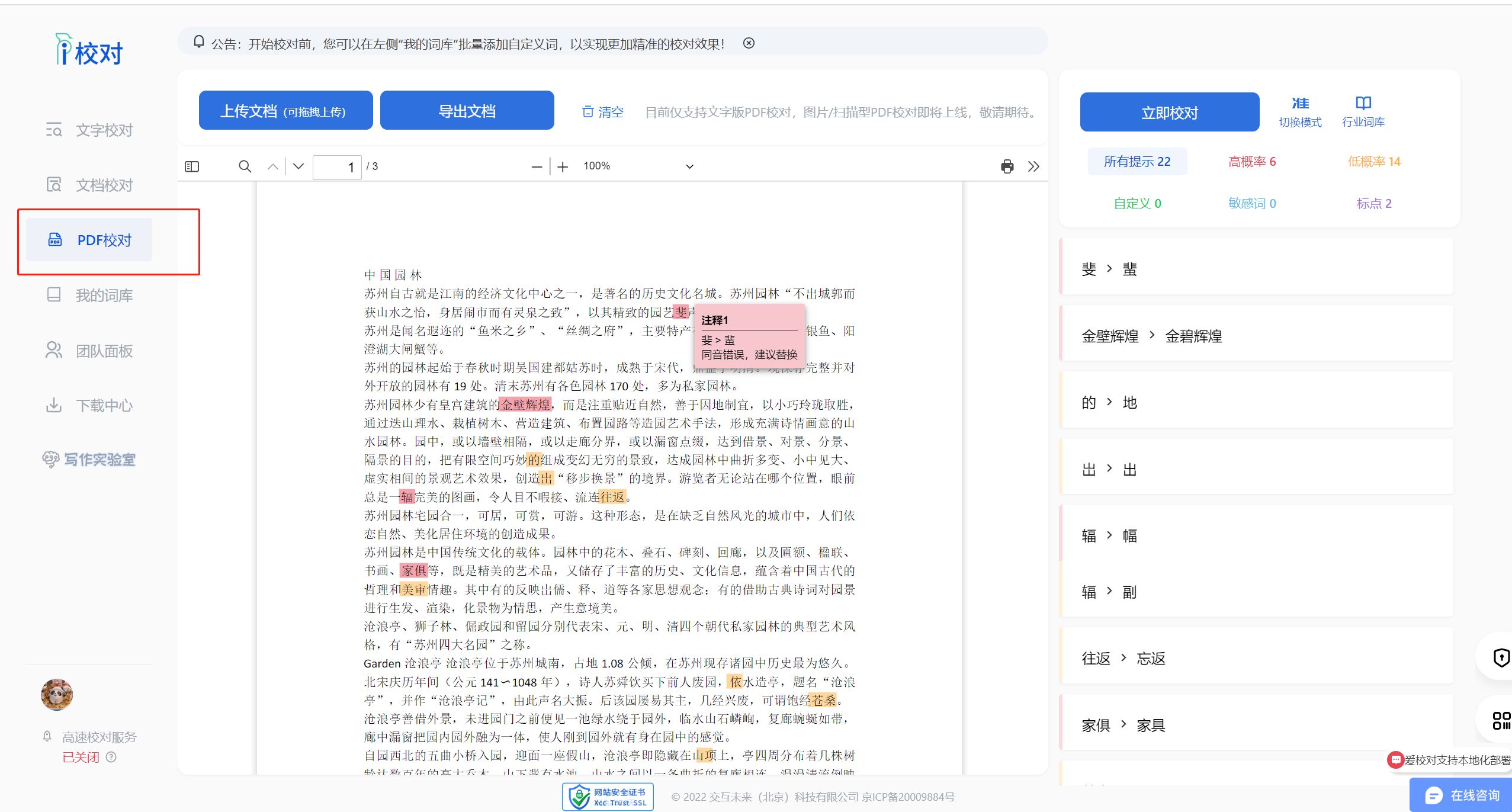
爱校对发布全新PDF校对工具,为用户带来更为便捷的校正体验
随着数字化文档使用的普及,PDF格式已经成为最为广泛使用的文件格式之一。为满足广大用户对于高效、准确PDF文档校对的需求,爱校对团队经过深入研发,正式推出全新的PDF校对工具! 这一全新工具针对PDF文件格式进行了深度优化&#…...

记录protocol buffers Mac安装
使用brew安装最新的protobuf 在Mac 上安装,使用brew 可以安装最新的protobuf。这个也比较简单,简单说一下。 首先先检查一下是否安装了brew。如果没有安装brew的话,请先安装brew.可以通过brew --version来检查 使用brew install protobuf 来…...
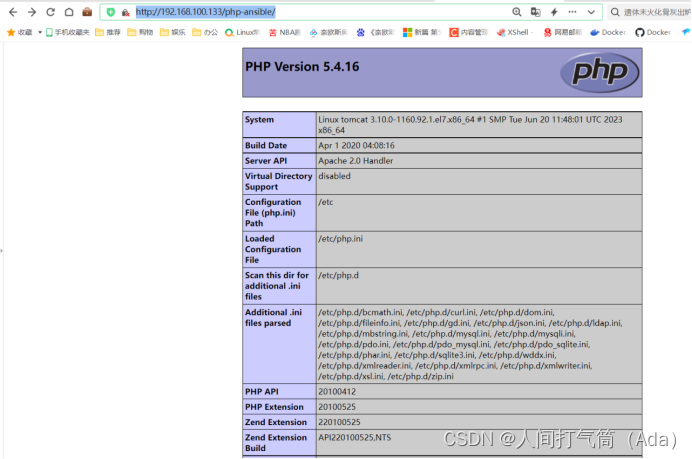
基于Jenkins自动打包并部署docker、PHP环境,ansible部署-------从小白到大神之路之学习运维第86天
第四阶段提升 时 间:2023年8月23日 参加人:全班人员 内 容: 基于Jenkins部署docker、PHP环境 目录 一、环境部署 (一)实验环境,服务器设置 (二)所有主机关闭防火墙和selinu…...
【附安装包】Midas Civil2019安装教程
软件下载 软件:Midas Civil版本:2019语言:简体中文大小:868.36M安装环境:Win11/Win10/Win8/Win7硬件要求:CPU2.5GHz 内存4G(或更高)下载通道①百度网盘丨64位下载链接:https://pan.…...
Apache StreamPark系列教程第一篇——安装和体验
一、StreamPark介绍 实时即未来,在实时处理流域 Apache Spark 和 Apache Flink 是一个伟大的进步,尤其是Apache Flink被普遍认为是下一代大数据流计算引擎, 我们在使用 Flink & Spark 时发现从编程模型, 启动配置到运维管理都有很多可以抽象共用的地方, 我们将一些好的经验…...

mysql replace insert update delete
目录 mysql replace && insert && update && delete replace mysql replace && insert && update && delete replace 我们在使用数据库时可能会经常遇到这种情况。如果一个表在一个字段上建立了唯一索引,当我们再向…...

实现SSM简易商城项目的商品查询功能
实现SSM简易商城项目的商品查询功能 介绍 在SSM(SpringSpringMVCMyBatis)框架下,我们可以轻松地实现一个简易商城项目。本博客将重点介绍如何实现商品查询功能,帮助读者了解并掌握该功能的开发过程。 步骤 1. 创建数据库表 首…...
视频批量剪辑矩阵分发系统源码开源分享----基于PHP语言
批量剪辑视频矩阵分发: 短视频seo主要基于抖音短视频平台,为企业实现多账号管理,视频分发,视频批量剪辑,抖音小程序搭建,企业私域转化等,本文主要介绍短视频矩阵系统抖音小程序开发详细及注意事…...

亚信科技AntDB数据库通过GB 18030-2022最高实现级别认证,荣膺首批通过该认证的产品之列
近日,亚信科技AntDB数据库通过GB 18030-2022《信息技术 中文编码字符集》最高实现级别(级别3)检测认证,成为首批通过该认证的数据库产品之一。 图1:AntDB通过GB 18030-2022最高实现级别认证 GB 18030《信息技术 中文编…...

第11章 优化多线程应用程序
对软件来说,为持续增长的CPU核数做好准备,对应用程序在未来的成功至关重要。 11.1 性能扩展和开销 通过可伸缩定律将计算单元(线程)之间的通信描述为影响性能的另一个门控因素。通用可伸缩定律描述性能劣化由多个因素导致&#…...
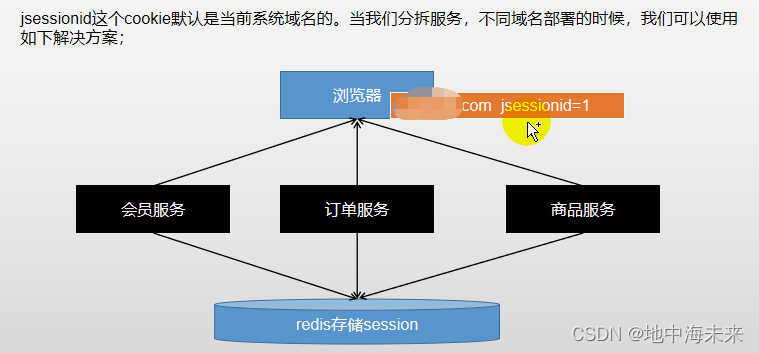
分布式下的session共享问题
首页我们确定在分布式的情况下session是不能共享的。 1.不同的服务,session不能共享,也就是微服务的情况下 2.同一服务在分布式情况,session同样不能共享,也会是分布式情况 分布式下session共享问题解决方案(域名相同) 1.session复…...
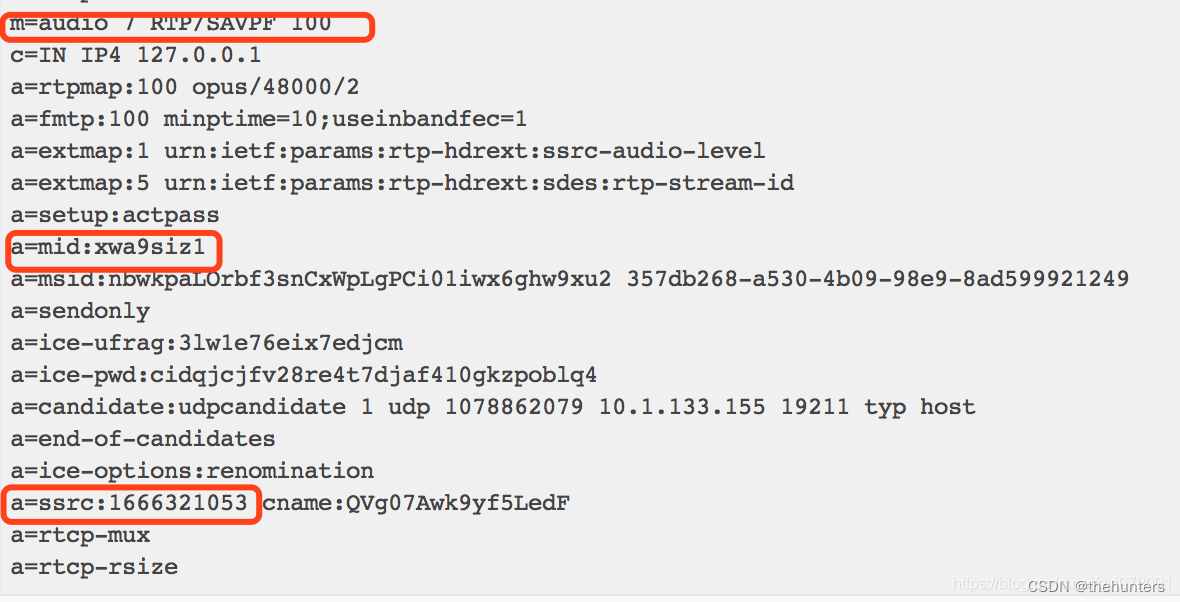
webrtc的Sdp中的Plan-b和UnifiedPlan
在一些类似于视频会议场景下,媒体会话参与者需要接收或者发送多个流,例如一个源端,同时发送多个左右音轨的音频,或者多个摄像头的视频流;在2013年,提出了2个不同的SDP IETF草案Plan B和Unified Plan&#x…...
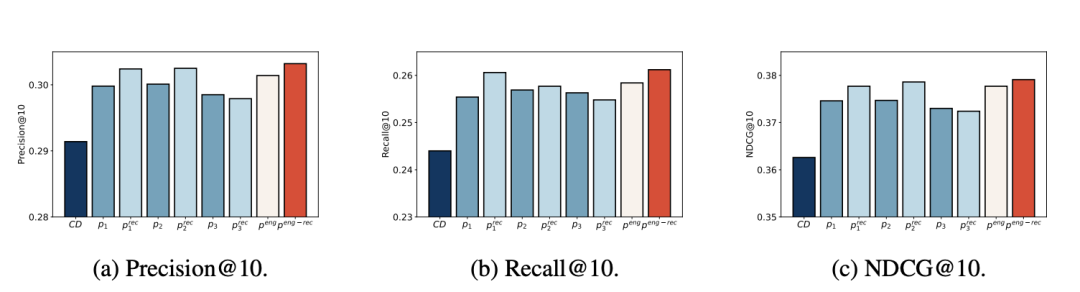
LLM-Rec:基于提示大语言模型的个性化推荐
1. 基本信息 论文题目:LLM-Rec: Personalized Recommendation via Prompting Large Language Models 作者:Hanjia Lyu, Song Jiang, Hanqing Zeng, Yinglong Xia, Jiebo Luo 机构:University of Rochester, University of California Los Angeles, Meta AI, University of Ro…...

microsoft -en - us 无法卸载
因为office2013 有漏洞,要进行升级,弄了个office2016,提示无法安装, microsoft visio -en - us 即点即用的存在。点击各种卸载,都无法生效。 再去搜了下软件使用评论,里面提到geek 可以卸载,下…...
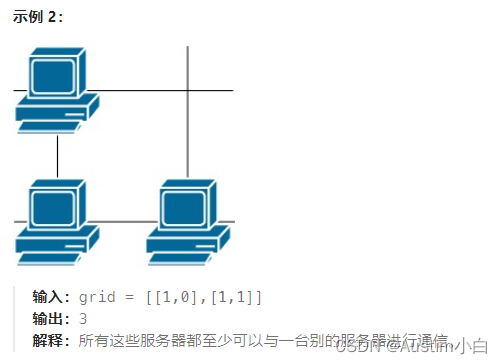
day43参与通信的服务器
1.题目描述 这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有。 如果两台服务器位于同一行或者同一列,我们就认为它们之间可以进行通信。 请你统计并返回能够与至少…...
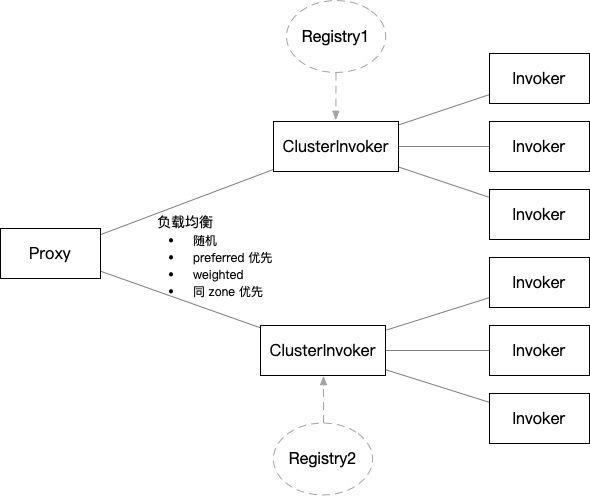
K8S如何部署ZooKeeper以及如何进行ZooKeeper的平滑替换
前言 在之前的章节中,我们已经成功地将Dubbo项目迁移到了云环境。在这个过程中,我们选择了单机ZooKeeper作为注册中心。接下来,我们将探讨如何将单机ZooKeeper部署到云端,以及在上云过程中可能遇到的问题及解决方案。 ZooKeeper…...

Leetcode刷题之1658. 将 x 减到 0 的最小操作数
题目: 算法分析: 可以看出,这道题本意是从计算两侧和为x 的数字, 要求数量最少, 那我们可以反向思考, 假如整个数组的和为sum, 那么我们就可以求中间部分和为sum-x的数字(当然必须连续), 当中间部分的数字同时达到和为sum-x以及长度最长两个要求时, 两侧数字也就达到了和为x以…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
