2023国赛数学建模思路 - 案例:粒子群算法
文章目录
- 1 什么是粒子群算法?
- 2 举个例子
- 3 还是一个例子
- 算法流程
- 算法实现
- 建模资料
# 0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 什么是粒子群算法?
粒子群算法(Particle Swarm Optimization,PSO)是一种模仿鸟群、鱼群觅食行为发展起来的一种进化算法。其概念简单易于编程实现且运行效率高、参数相对较少,应用非常广泛。粒子群算法于1995年提出,距今(2019)已有24年历史。
粒子群算法中每一个粒子的位置代表了待求问题的一个候选解。每一个粒子的位置在空间内的好坏由该粒子的位置在待求问题中的适应度值决定。每一个粒子在下一代的位置有其在这一代的位置与其自身的速度矢量决定,其速度决定了粒子每次飞行的方向和距离。在飞行过程中,粒子会记录下自己所到过的最优位置 P,群体也会更新群体所到过的最优位置G 。粒子的飞行速度则由其当前位置、粒子自身所到过的最优位置、群体所到过的最优位置以及粒子此时的速度共同决定。

2 举个例子
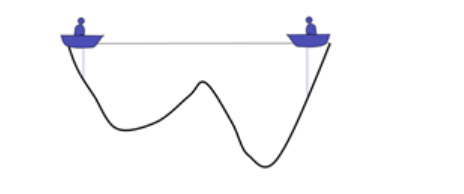
在一个湖中有两个人他们之间可以通信,并且可以探测到自己所在位置的最低点。初始位置如上图所示,由于右边比较深,因此左边的人会往右边移动一下小船。
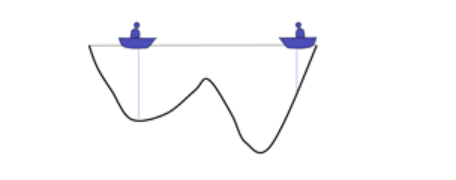
现在左边比较深,因此右边的人会往左边移动一下小船
一直重复该过程,最后两个小船会相遇
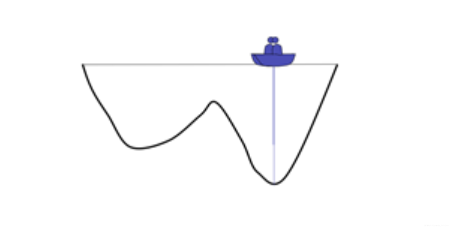
得到一个局部的最优解
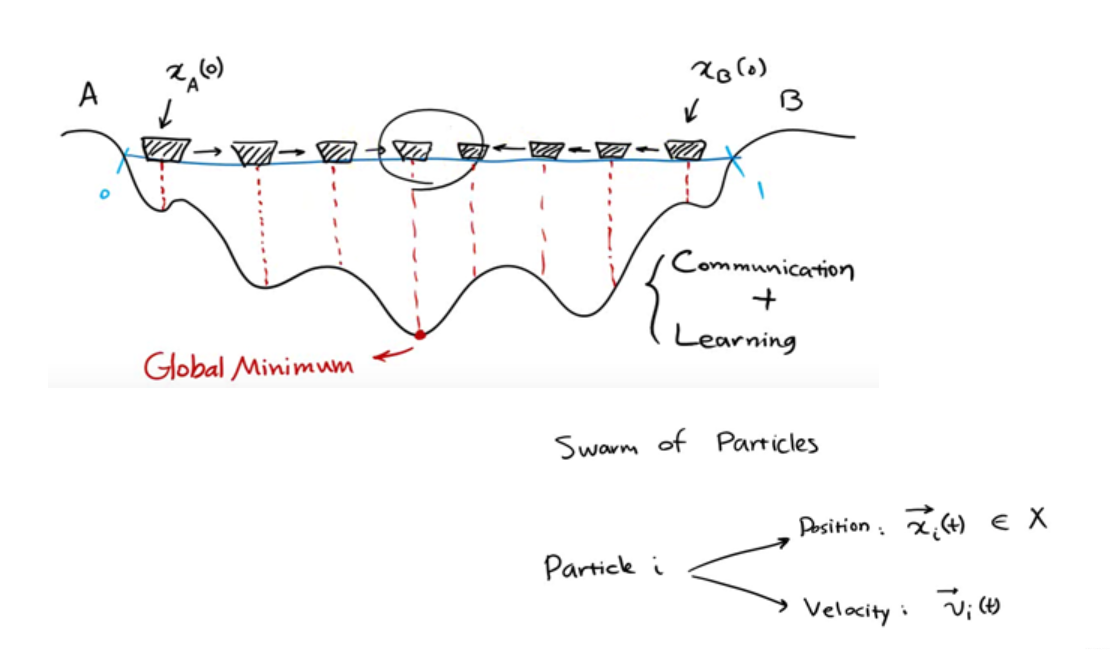 将每个个体表示为粒子。每个个体在某一时刻的位置表示为,x(t),方向表示为v(t)
将每个个体表示为粒子。每个个体在某一时刻的位置表示为,x(t),方向表示为v(t)
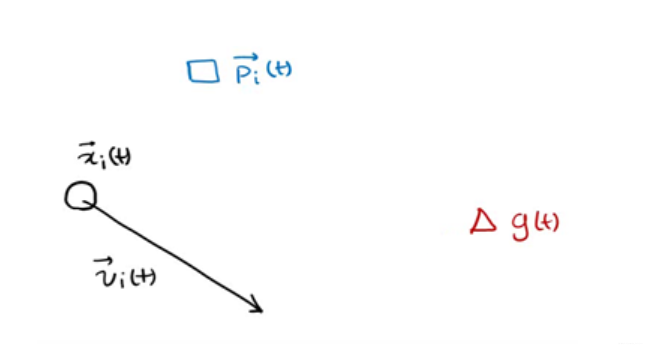
p(t)为在t时刻x个体的自己的最优解,g(t)为在t时刻所有个体的最优解,v(t)为个体在t时刻的方向,x(t)为个体在t时刻的位置
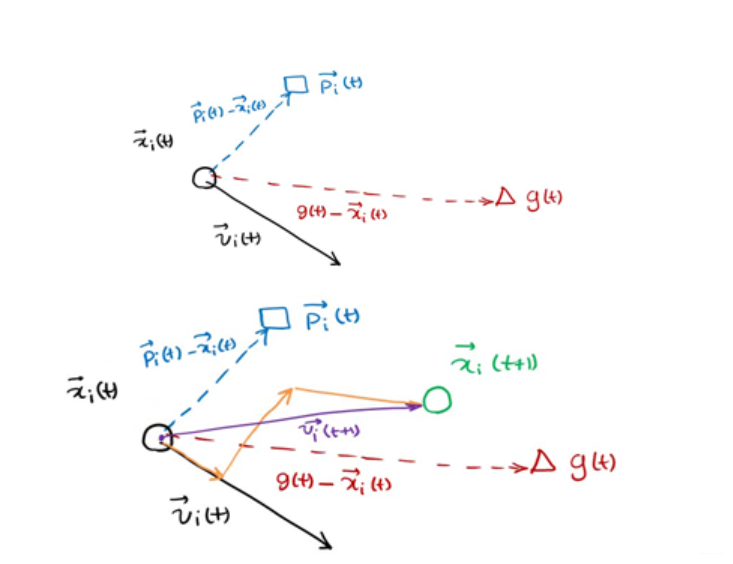
下一个位置为上图所示由x,p,g共同决定了
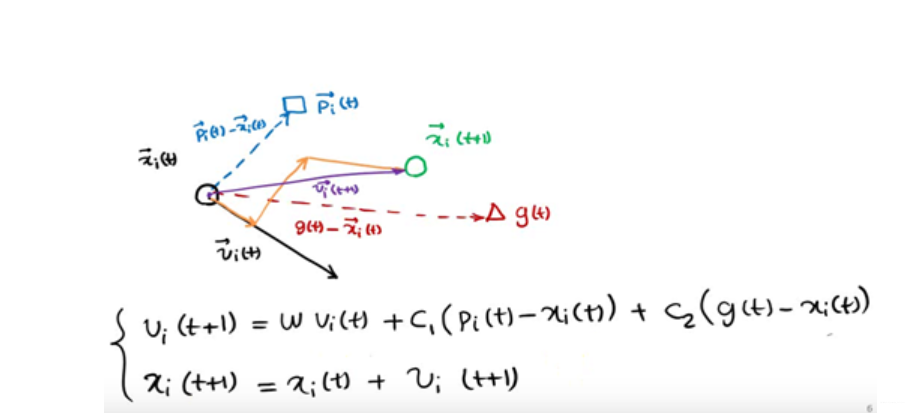
种群中的粒子通过不断地向自身和种群的历史信息进行学习,从而可以找到问题的最优解。
3 还是一个例子
粒子群算法是根据鸟群觅食行为衍生出的算法。现在,我们的主角换成是一群鸟。

小鸟们的目标很简单,要在这一带找到食物最充足的位置安家、休养生息。它们在这个地方的搜索策略如下:
1. 每只鸟随机找一个地方,评估这个地方的食物量。
2. 所有的鸟一起开会,选出食物量最多的地方作为安家的候选点G。
3. 每只鸟回顾自己的旅程,记住自己曾经去过的食物量最多的地方P。
4. 每只鸟为了找到食物量更多的地方,于是向着G飞行,但是呢,不知是出于选择困难症还是对P的留恋,或者是对G的不信任,小鸟向G飞行时,时不时也向P飞行,其实它自己也不知道到底是向G飞行的多还是向P飞行的多。
5. 又到了开会的时间,如果小鸟们决定停止寻找,那么它们会选择当前的G来安家;否则继续2->3->4->5来寻找它们的栖息地。
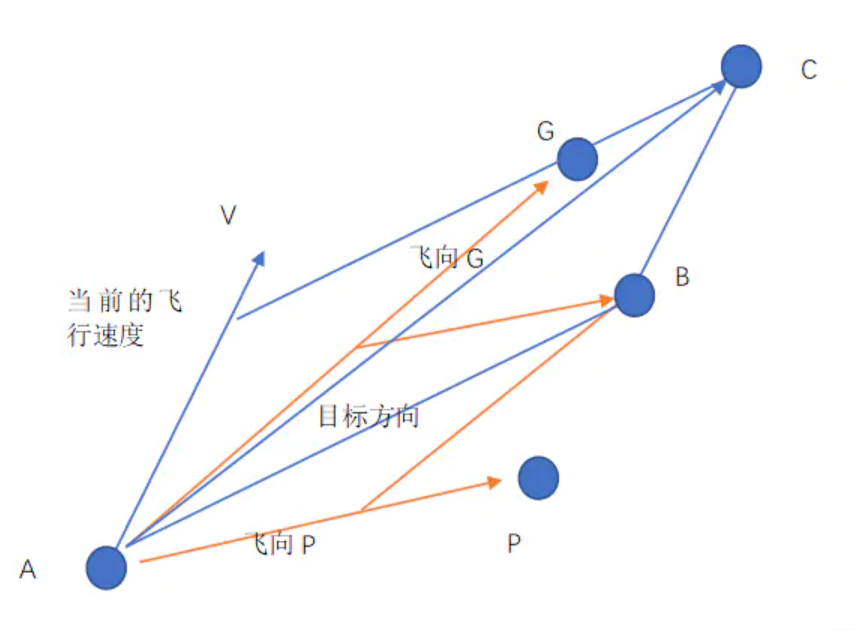
上图描述的策略4的情况,一只鸟在点A处,点G是鸟群们找到过的食物最多的位置,点P是它自己去过的食物最多的地点。V是它现在的飞行速度(速度是矢量,有方向和大小),现在它决定向着P和G飞行,但是这是一只佛系鸟,具体飞多少随缘。如果没有速度V,它应该飞到B点,有了速度V的影响,它的合速度最终使它飞到了点C,这里是它的下一个目的地。如果C比P好那么C就成了下一次的P,如果C比G好,那么就成了下一次的G。
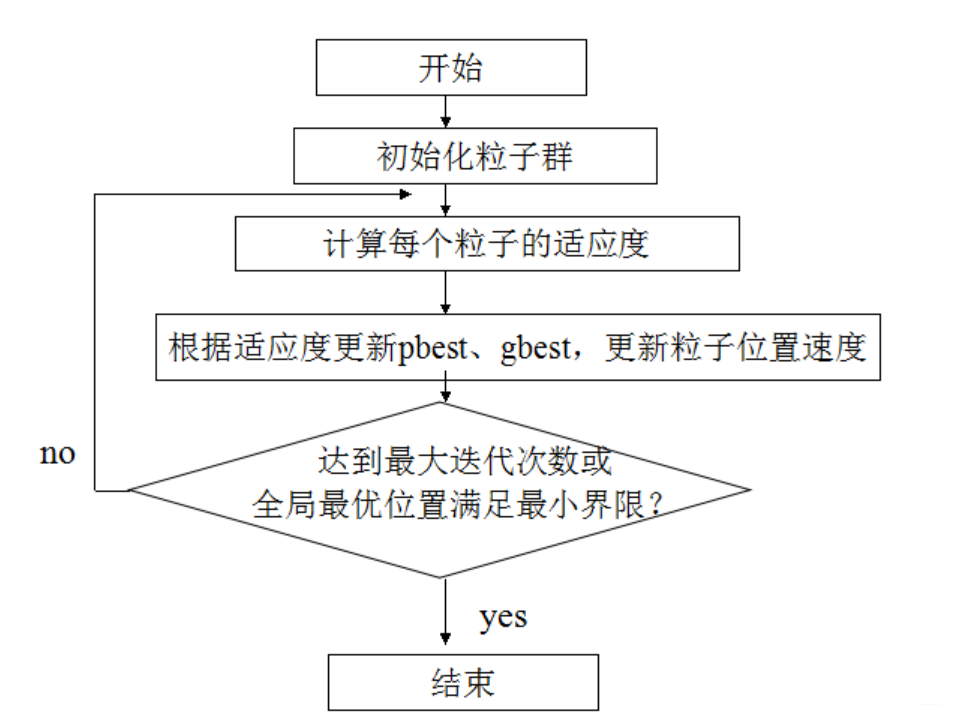
算法流程
算法实现
这里学长用python来给大家演示使用粒子群解函数最优解
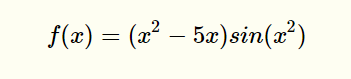
import numpy as np
import matplotlib.pyplot as plt
import random# 定义“粒子”类
class parti(object):def __init__(self, v, x):self.v = v # 粒子当前速度self.x = x # 粒子当前位置self.pbest = x # 粒子历史最优位置class PSO(object):def __init__(self, interval, tab='min', partisNum=10, iterMax=1000, w=1, c1=2, c2=2):self.interval = interval # 给定状态空间 - 即待求解空间self.tab = tab.strip() # 求解最大值还是最小值的标签: 'min' - 最小值;'max' - 最大值self.iterMax = iterMax # 迭代求解次数self.w = w # 惯性因子self.c1, self.c2 = c1, c2 # 学习因子self.v_max = (interval[1] - interval[0]) * 0.1 # 设置最大迁移速度#####################################################################self.partis_list, self.gbest = self.initPartis(partisNum) # 完成粒子群的初始化,并提取群体历史最优位置self.x_seeds = np.array(list(parti_.x for parti_ in self.partis_list)) # 提取粒子群的种子状态 ###self.solve() # 完成主体的求解过程self.display() # 数据可视化展示def initPartis(self, partisNum):partis_list = list()for i in range(partisNum):v_seed = random.uniform(-self.v_max, self.v_max)x_seed = random.uniform(*self.interval)partis_list.append(parti(v_seed, x_seed))temp = 'find_' + self.tabif hasattr(self, temp): # 采用反射方法提取对应的函数gbest = getattr(self, temp)(partis_list)else:exit('>>>tab标签传参有误:"min"|"max"<<<')return partis_list, gbestdef solve(self):for i in range(self.iterMax):for parti_c in self.partis_list:f1 = self.func(parti_c.x)# 更新粒子速度,并限制在最大迁移速度之内parti_c.v = self.w * parti_c.v + self.c1 * random.random() * (parti_c.pbest - parti_c.x) + self.c2 * random.random() * (self.gbest - parti_c.x)if parti_c.v > self.v_max: parti_c.v = self.v_maxelif parti_c.v < -self.v_max: parti_c.v = -self.v_max# 更新粒子位置,并限制在待解空间之内if self.interval[0] <= parti_c.x + parti_c.v <=self.interval[1]:parti_c.x = parti_c.x + parti_c.velse:parti_c.x = parti_c.x - parti_c.vf2 = self.func(parti_c.x)getattr(self, 'deal_'+self.tab)(f1, f2, parti_c) # 更新粒子历史最优位置与群体历史最优位置def func(self, x): # 状态产生函数 - 即待求解函数value = np.sin(x**2) * (x**2 - 5*x)return valuedef find_min(self, partis_list): # 按状态函数最小值找到粒子群初始化的历史最优位置parti = min(partis_list, key=lambda parti: self.func(parti.pbest))return parti.pbestdef find_max(self, partis_list):parti = max(partis_list, key=lambda parti: self.func(parti.pbest)) # 按状态函数最大值找到粒子群初始化的历史最优位置return parti.pbestdef deal_min(self, f1, f2, parti_):if f2 < f1: # 更新粒子历史最优位置parti_.pbest = parti_.xif f2 < self.func(self.gbest):self.gbest = parti_.x # 更新群体历史最优位置def deal_max(self, f1, f2, parti_):if f2 > f1: # 更新粒子历史最优位置parti_.pbest = parti_.xif f2 > self.func(self.gbest):self.gbest = parti_.x # 更新群体历史最优位置def display(self):print('solution: {}'.format(self.gbest))plt.figure(figsize=(8, 4))x = np.linspace(self.interval[0], self.interval[1], 300)y = self.func(x)plt.plot(x, y, 'g-', label='function')plt.plot(self.x_seeds, self.func(self.x_seeds), 'b.', label='seeds')plt.plot(self.gbest, self.func(self.gbest), 'r*', label='solution')plt.xlabel('x')plt.ylabel('f(x)')plt.title('solution = {}'.format(self.gbest))plt.legend()plt.savefig('PSO.png', dpi=500)plt.show()plt.close()if __name__ == '__main__':PSO([-9, 5], 'max')
效果
建模资料
资料分享: 最强建模资料


相关文章:

2023国赛数学建模思路 - 案例:粒子群算法
文章目录 1 什么是粒子群算法?2 举个例子3 还是一个例子算法流程算法实现建模资料 # 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 什么是粒子群算法? 粒子群算法(Pa…...
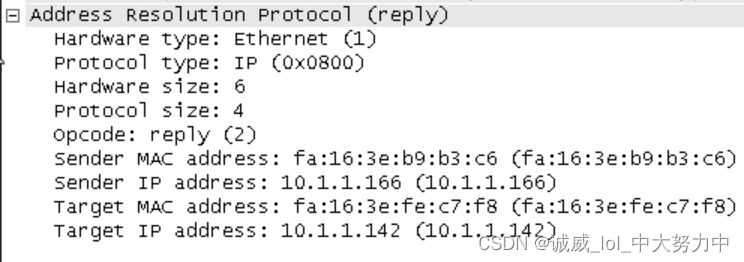
Wireshark数据抓包分析之ARP协议
一、实验目的: 通过wireshark的数据抓包了解这个ARP协议的具体内容 二、预备知识: 1.Address Resolution Protocol协议,就是通过目标IP的值,获取到目标的mac地址的一个协议 2.ARP协议的详细工作过程,下面描述得非常清晰ÿ…...
6个比较火的AI绘画生成工具
随着人工智能技术的发展,市场上出现了越来越多的人工智能图像生成工具。这些人工智能图像生成工具可以自动创建惊人的图像、艺术作品和设计,以帮助设计师和创意人员更快地实现他们的创造性想法。在本文中,我们将推荐7种最近流行的人工智能图像…...

静力水准仪说明介绍
静力水准仪是测量两点间或多点间相对高程变化的仪器。由储液器、高精度芯体和特别定制电路模块、保护罩等部件组成。沉降系统由多个同型号传感器组成,储液罐之间由通气管和通液管相连通,基准点置于一个稳定的水平基点,当测点相对于基准点发生…...

HAProxy 高级功能与配置
HAProxy 高级功能与配置 配置和验证的环境看这篇文章:HAProxy 各种调度算法介绍 一.基于 cookie 的会话保持 使用cookie关键字来配置后端服务器基于 cookie 的会话持久连接。 配置格式 cookie <name> [ rewrite | insert | prefix ] [ indirect ] [ nocache ][ post…...
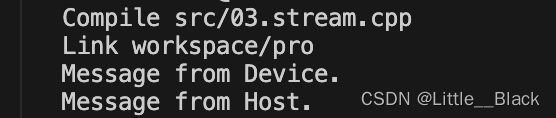
cuda编程002—流
没有使用同步的情况: #include <stdio.h> #include <cuda_runtime.h>__global__ void test_kernel(){printf("Message from Device.\n"); } void test(){test_kernel<<<1, 1>>>(); } #include <cuda_runtime.h> #i…...

2023年国赛 高教社杯数学建模思路 - 案例:粒子群算法
文章目录 1 什么是粒子群算法?2 举个例子3 还是一个例子算法流程算法实现建模资料 # 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 什么是粒子群算法? 粒子群算法(Pa…...
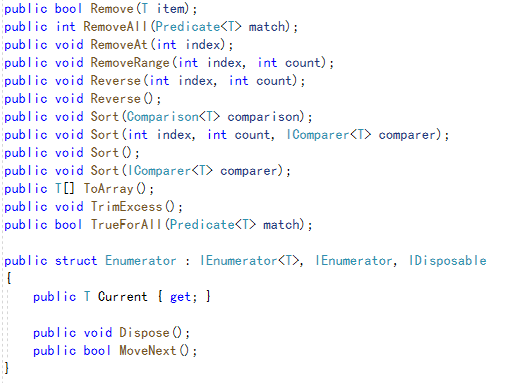
【C#学习笔记】数据类中常用委托及接口——以List<T>为例
文章目录 List\<T\>/LinkedList \<T\>为什么是神?(泛型为什么是神)一些常见,通用的委托和接口ComparisonEnumerator List<T>/LinkedList <T>为什么是神?(泛型为什么是神࿰…...

idea的断点调试
1、行断点 首先在代码的最左侧点击会显示红色的圆圈 第二步在main方法中右键选中debug run进行运行 会出现下面图片的情况 出现上图之后,点击console 下一步 这个时候就可以看到调试的结果了 6、方法调用栈:这里显示了该线程调试所经过的所有方法&…...

vue和react学哪一个比较有助于以后发展?
前言 首先声明vue和react这两个框架都是很优秀的前端框架,使用的人群下载量上数量也是相当的庞大,这篇文章没有贬低或者攻击任何一个框架的意思,只在于根据答主的问题来对这两个框架做出对比,以方便大家更加清晰的了解到当下vue和…...

【SkyWalking】分布式服务追踪与调用链系统
1、基本介绍 SkyWalking是一个开源的观测平台,官网:Apache SkyWalking; 可监控:分布式追踪调用链 、jvm内存变化、监控报警、查看服务器基本配置信息。 2、SkyWalking架构原理 在整个skywalking的系统中,有三个角色&am…...
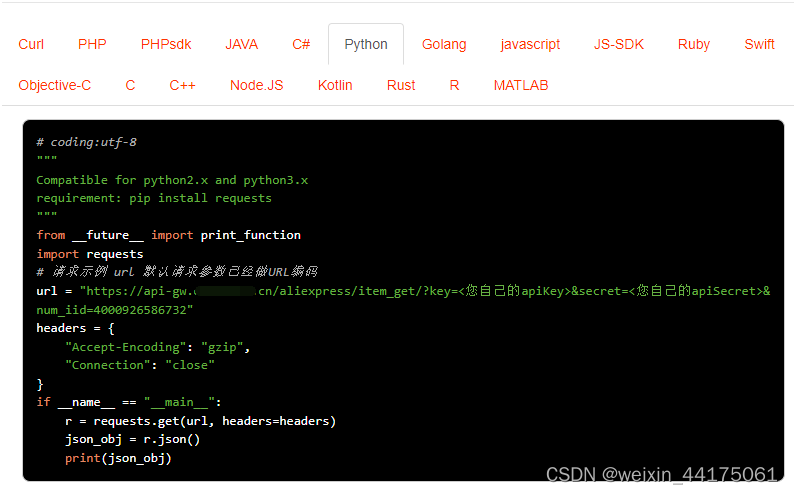
Python“牵手”速卖通商品详情API接口运用场景及功能介绍
速卖通电商API接口是针对速卖通提供的电商服务平台,为开发人员提供了简单、可靠的技术来与速卖通电商平台进行数据交互,实现一系列开发、管理和营销等操作。其中包括商品详情API接口,通过这个API接口商家可以获取商品的详细信息,包…...

java调用python脚本的示例
java调用python脚本的示例 import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader;public class JavaCallPythonScript {public static void main(String[] args) {// 调用Python脚本的命令String pythonScriptPath "path/to/y…...
)
【C语言】柔性数组(可边长数组)
一、介绍 柔性数组(Flexible Array),又称可变长数组。一般数组的长度是在编译时确定,而柔性数组对象的长度在运行时确定。在定义结构体时允许创建一个空数组(例如:arr [ 0 ] ),该数…...
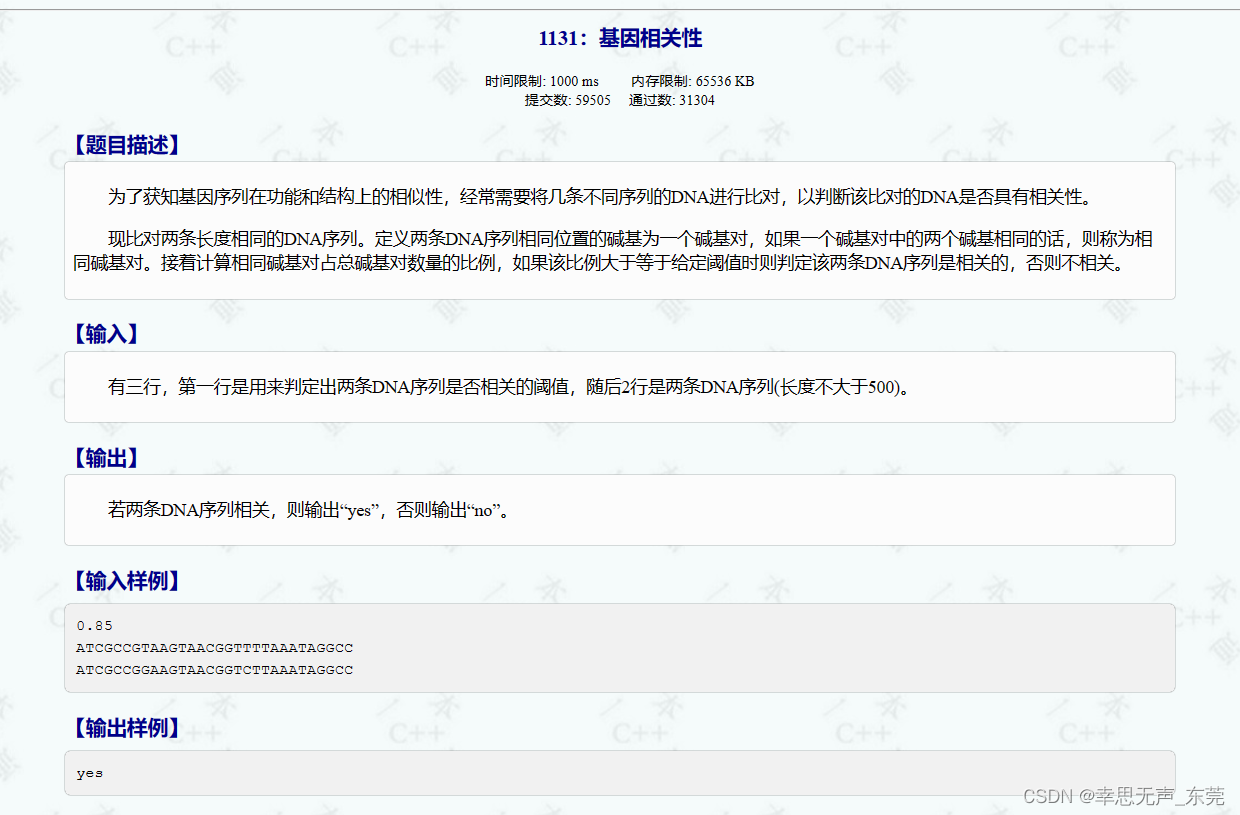
C++信息学奥赛1131:基因相关性
这段代码的功能是比较两个字符串的相似度,并根据给定的阈值判断是否相似。 解析注释后的代码如下: #include <iostream> #include <string> using namespace std;int main() {double bf; // 定义双精度浮点数变量bf,用于存储阈…...

如何保证分布式系统中服务的高可用性:应对 ZooKeeper Leader 节点故障的注册处理策略
推荐阅读 AI文本 OCR识别最佳实践 AI Gamma一键生成PPT工具直达链接 玩转cloud Studio 在线编码神器 玩转 GPU AI绘画、AI讲话、翻译,GPU点亮AI想象空间 资源分享 「java、python面试题」来自UC网盘app分享,打开手机app,额外获得1T空间 https://dr…...

SQL注入之延时注入
文章目录 延时注入是什么?延时注入获取数据库版本号 延时注入是什么? 延时注入就是利用sleep()函数通过if语句判断所写的语句真假,如果为真返回我们想要的东西(例如:数据库的长度,数据库的名字等࿰…...
运维高级学习--Docker(二)
1、使用mysql:5.6和 owncloud 镜像,构建一个个人网盘。 #拉取mysql5.6和owncloud镜像 [rootlocalhost ~]# docker pull mysql:5.6 [rootlocalhost ~]# docker pull owncloud [rootlocalhost ~]# docker images REPOSITORY TAG IMAGE ID CREATED …...
QT的核心——信号与槽
目录 回顾C 语言信号 1、信号与槽 2、关联信号与槽 2.1自动关联信号与槽 2.2手动关联信号与槽 2.3断开信号与槽 3、自定义信号 3.1自定义信号使用条件 3.2自定义槽函数使用条件 4、信号与槽参数传递 4.1自定义一个带参的信号 4.2关联带参的信号与槽 4.3发送一个带…...
【业务功能篇73】web系统架构演变-单体-集群-垂直化-服务化-微服务化
1.服务架构的演 1.1 单体架构 单体架构应该是我们最先接触到的架构实现了,在单体架构中使用经典的三层模型,即表现层,业务逻辑层和数据访问层。 单体架构只适合在应用初期,且访问量比较下的情况下使用,优点是性价比很…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
