【GUI】基于开关李雅普诺夫函数的非线性系统稳定(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
摘要:
如果李雅普诺夫函数已知,则可以稳定动态系统。然而,计算李雅普诺夫函数通常具有挑战性。本文采用了一种新的方法;它假设一个基本的类似李雅普诺夫的函数,然后试图在数值上减少李雅普诺夫值。如果控制工作在任何迭代中都没有效果,则切换类似李雅普诺夫的函数以尝试重新获得控制权。该方法在四个模拟系统上进行了测试,以对其有用性和局限性提供一些看法。高度耦合的三阶系统证明了该方法的一般适用性,最后考虑了机器人应用中3个电机的协调控制。
最初,Lyapunov理论被用于检验非线性系统的稳定性[1]。1983年,Artstein[2]开始使用Lyapunov理论进行控制器综合。他证明了Lyapunov函数存在当且仅当系统是可稳定的。
找到合适的李雅普诺夫函数可能很困难,但如果能找到,那么就可以用一个简单的公式计算出稳定控制的努力。除了Artstein的原始方法之外,当Lyapunov函数已知时,还有其他几种方法[3,4]来计算稳定控制努力。
许多研究者提出了寻找Lyapunov函数的创造性方法,包括[3-6]。然而,这些李亚普诺夫函数*处理了操作系统仅适用于本地,或者它们仅限于系统的一个子集。
一般来说,如何找到Lyapunov函数的问题仍然没有解决[4]。
Peleties[7]开创了分段动态系统的多个“Lyapunov”函数的概念,当整个感兴趣区域的单个Lyapunov函数未知或会导致过度保守的控制策略时,这是有用的。2013年,Sassano[8]提出了时变Lyapunov函数的概念。他的技术可以生成一个李雅普诺夫函数,而不需要解李雅普诺夫偏微分不等式,尽管它需要解另一个偏微分方程。所提出的方法在概念上类似于[7,8],因为它涉及一个动态的李雅普诺夫函数。它涉及到在默认值失去控制时在两个详尽的lyapunov类函数之间切换。与[8]一样,本文提出的方法不需要明确了解Lyapunov函数。与[7]相比,所提出的方法的优点是它不局限于特定形式的系统。与[8]相比,优点是该技术是全局适用的,并且不需要解偏微分方程。
📚2 运行结果
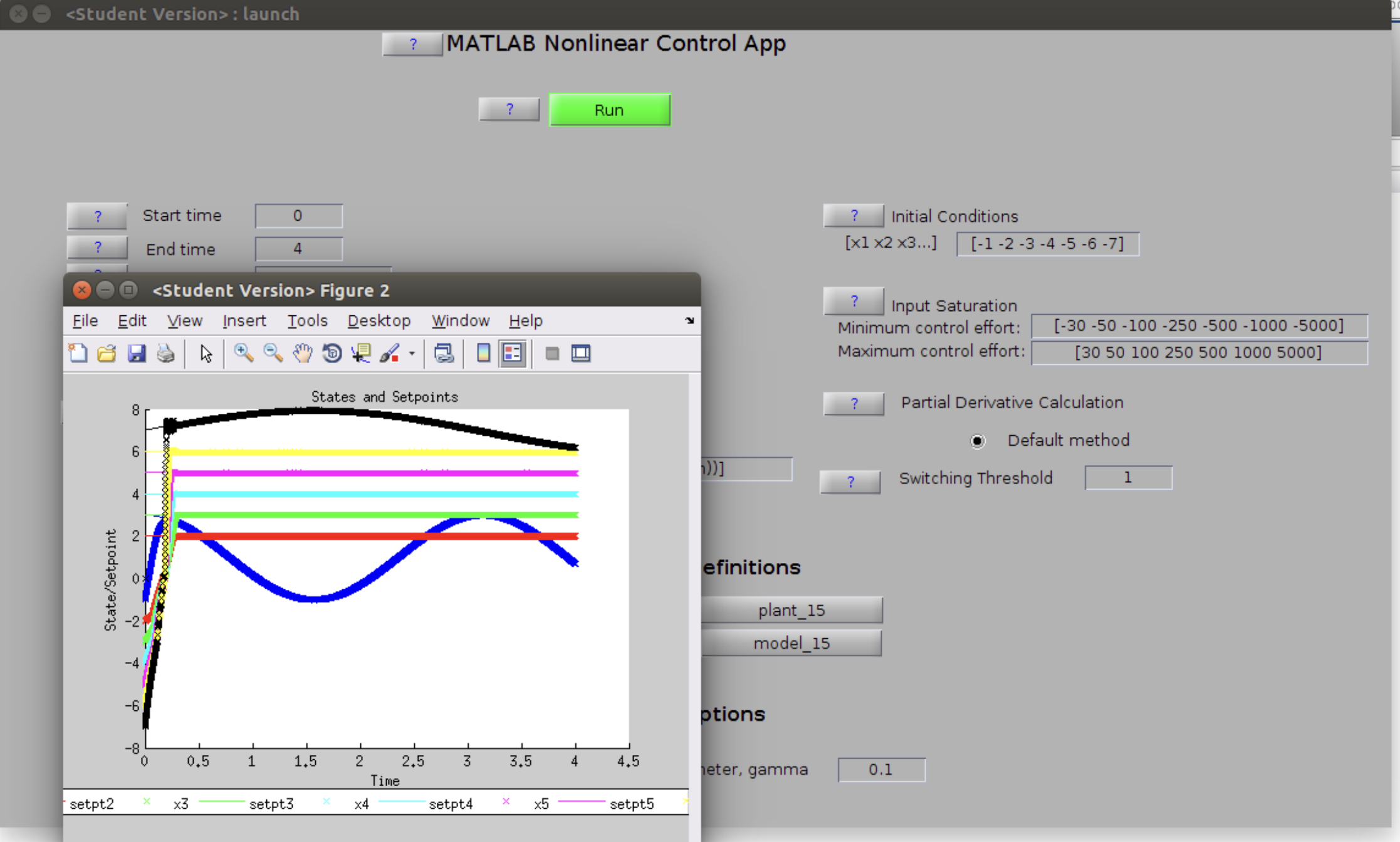
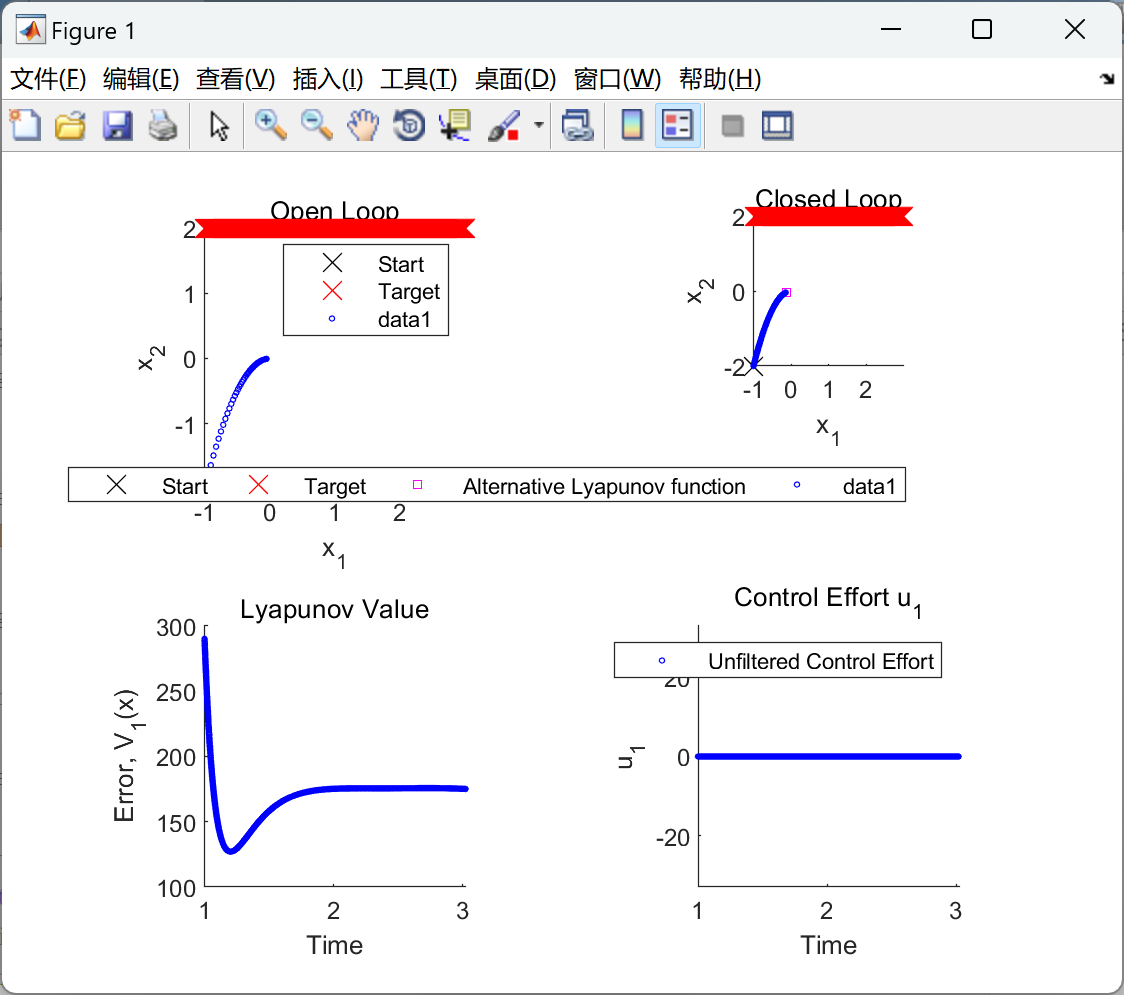
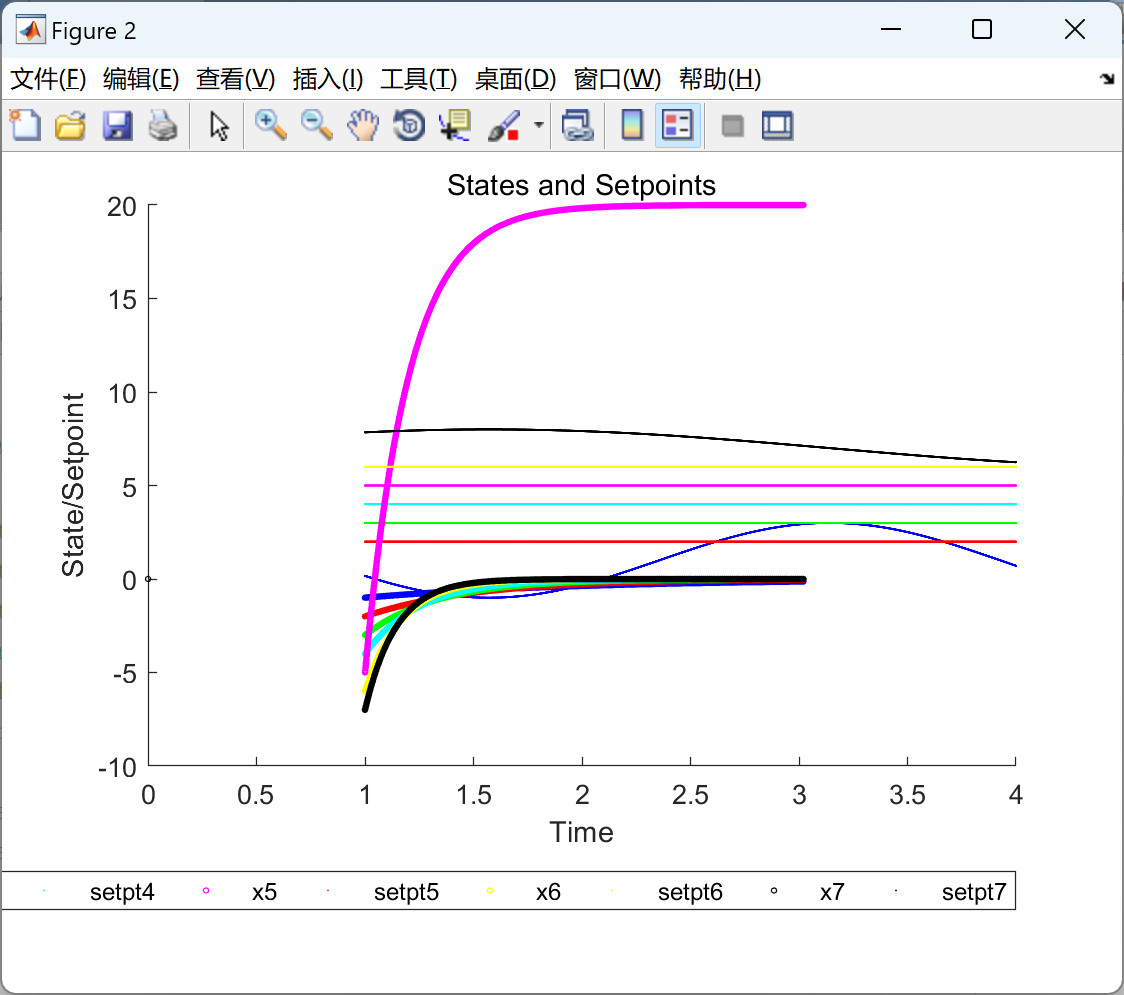
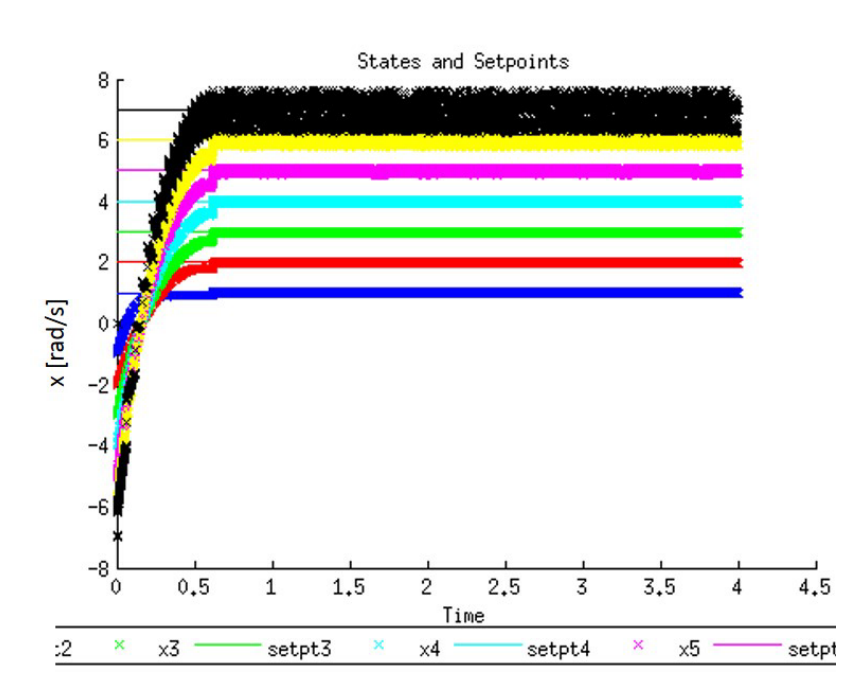
部分代码:
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @launch_OpeningFcn, ...
'gui_OutputFcn', @launch_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback', []);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT
addpath(genpath(pwd))
% --- Executes just before launch is made visible.
function launch_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% varargin command line arguments to launch (see VARARGIN)
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。

🌈4 Matlab代码实现
相关文章:

【GUI】基于开关李雅普诺夫函数的非线性系统稳定(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
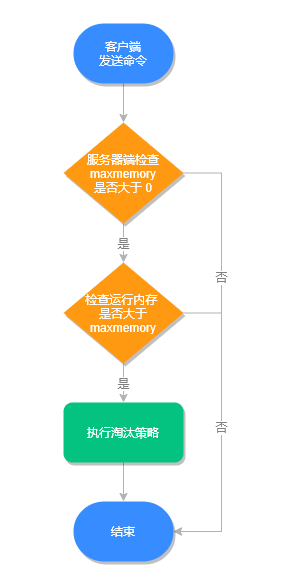
Redis 缓存满了怎么办?
引言 Redis 缓存使用内存来保存数据,随着需要缓存的数据量越来越大,有限的缓存空间不可避免地会被写满。此时,应该怎么办?本篇文章接下来就来聊聊缓存满了之后的数据淘汰机制。 值得注意的是,在 Redis 中 过期策略 和…...
Grafana 安装配置教程
Grafana 安装配置教程 一、介绍二、Grafana 安装及配置2.1 下载2.2 安装2.2.1 windows安装 - 图形界面2.2.2 linux安装 - 安装脚本 三、Grafana的基本配置3.1 登录3.2 Grafana设置中文 四、grafana基本使用 一、介绍 Grafana是一个通用的可视化工具。对于Grafana而言࿰…...

【Linux】临界资源和临界区
目录 一、临界资源 二、如何实现对临界资源的互斥访问 1、互斥量 2、信号量 3、临界区 三、临界区 四、进程进入临界区的调度原则 一、临界资源 概念:临界资源是一次仅允许一个进程使用的共享资源,如全局变量等。 二、如何实现对临界资源的互斥访问 …...

拓扑排序Topological sorting/DFS C++应用例题P1113 杂务
拓扑排序 拓扑排序可以对DFS的基础上做变更从而达到想要的排序效果。因此,我们需要xy准备,vis数组记录访问状态,每一个任务都可以在dfs的过程中完成。 在使用拓扑排序方法时一些规定: 通常使用一个零时栈不会直接输出排序的节点…...
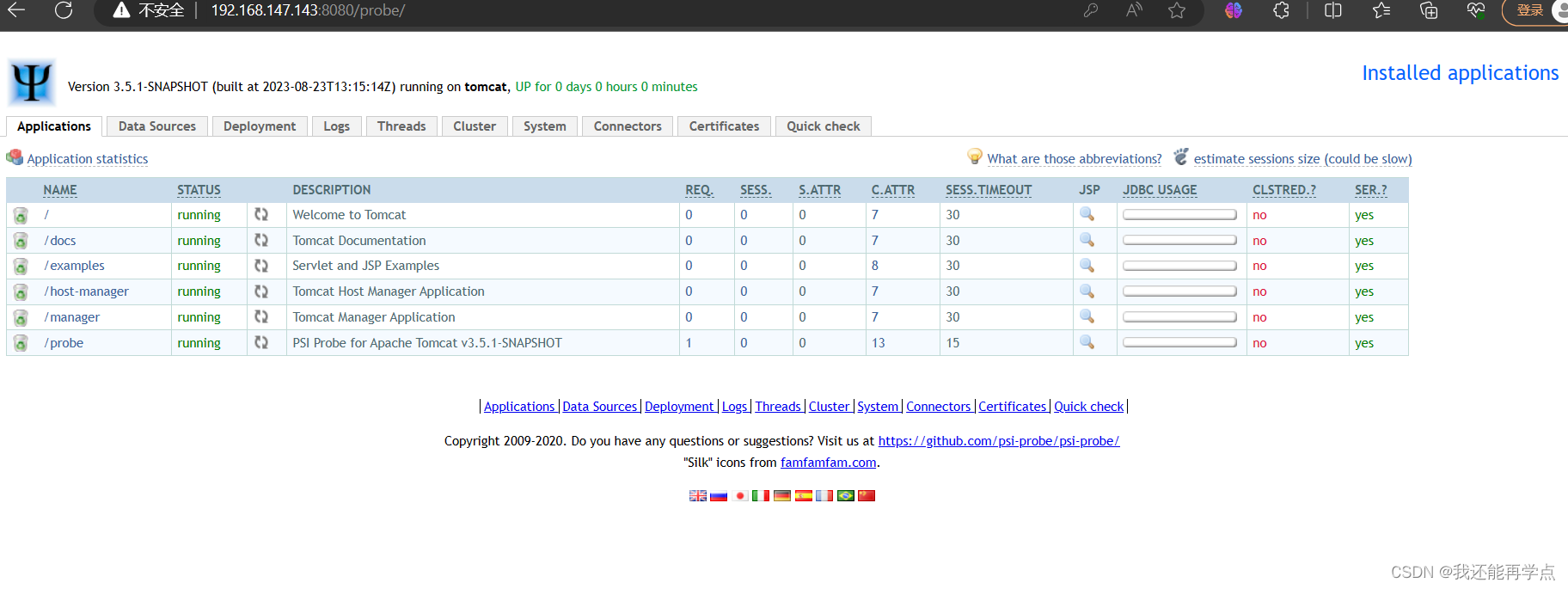
基于jenkins构建生成CICD环境
目录 一、安装配置jenkins 1、环境配置 2、软件要求 3、jdk安装(我是最小化安装,UI自带java要先删除rm -rf /usr/local/java 4、安装jenkins-2.419-1.1 二、Jenkins配置 1、修改jenkins初始密码 2、安装 Jenkins 必要插件 3、安装 Publish Over SS…...
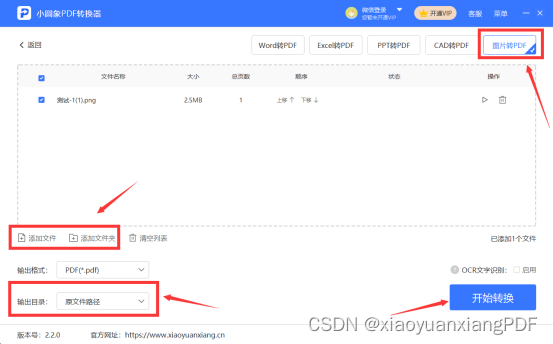
在线图片怎么转换成PDF?在线图片转换成PDF步骤介绍
文件格式要转化不知道怎么办?想要网上下载文件格式转换软件,但是却不知道下载哪个好?今天小编小编就给大家分享一下靠谱的小圆象PDF转换器工具,想知道这款软件好不好用?在线图片怎么转换成PDF?那就进来看看吧。 在线图片怎么转换成PDF 小圆象PDF转换…...
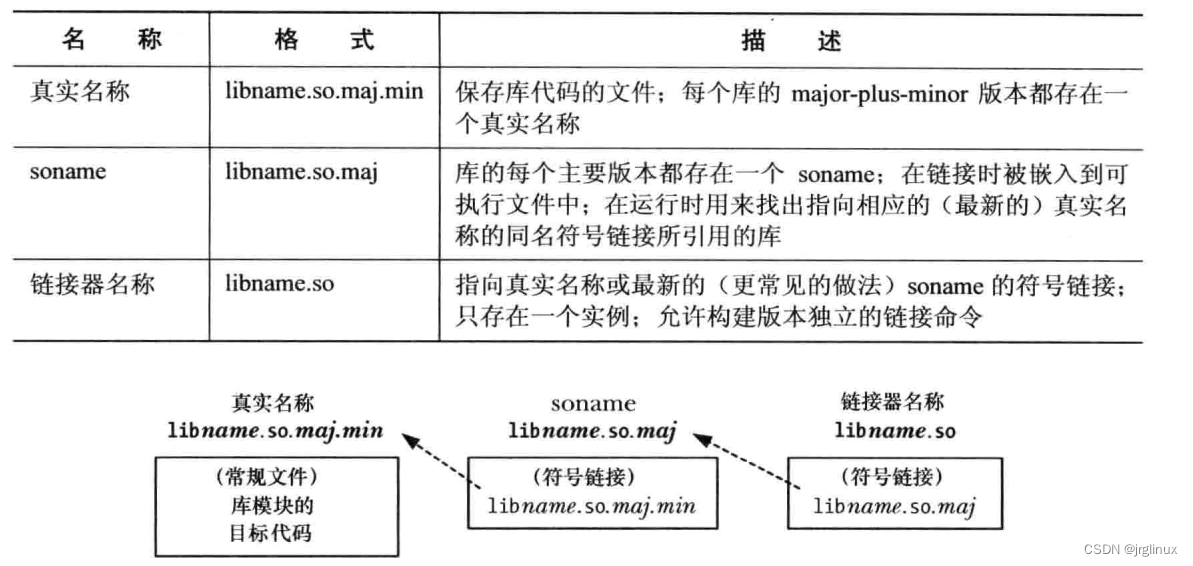
Linux共享库基础及实例
共享库是将库函数打包成一个可执行文件,使得其在运行时可以被多个进程共享。 目标库 回顾下构建程序的一种方式: 将每个源文件编译成目标文件,再通过链接器将这些目标文件链接组成一个可执行程序。 gcc -g -c prog.c mod1.c mod2.c gcc -g …...

java八股文面试[java基础]——final 关键字作用
为什么局部内部类和匿名内部类只能访问final变量: 知识来源 【基础】final_哔哩哔哩_bilibili...
Redis 分布式锁存在什么问题 ?如何解决 ?
目录 1. 如何实现分布式锁 2. Redis 分布式锁存在什么问题 2.1 解决死锁问题 2.2 解决锁误删问题 1. 如何实现分布式锁 Redis 天生就可以作为一个分布式系统来使用,所以它实现的锁都是分布式锁。 Redis 可以通过 setnx(set if not exists)…...

n5173b是德科技keysight N5173B信号发生器
产品概述 是德科技/安捷伦N5173B EXG模拟信号发生器 当您需要平衡预算和性能时,是德科技N5173B EXG微波模拟信号发生器是经济高效的选择。它提供解决宽带滤波器、放大器、接收机等参数测试的基本信号。执行基本LO上变频或CW阻塞,低成本覆盖13、20、31.…...
------ 实现多节点的Diff算法)
React源码解析18(10)------ 实现多节点的Diff算法
摘要 在上一篇中,实现了多节点的渲染。但是之前写得diff算法,只能适用于单节点的情况,例如这种情况: <div><p><span></span></p> </div>如果对于多节点的情况: <ul><…...

Linux指令篇!
Linux 是一个广泛使用的开源操作系统,以下是一些常用的 Linux 知识点和指令: 1. 文件和目录操作: - ls:列出目录内容 - cd:切换目录 - pwd:显示当前工作目录 - mkdir:创建目录 - touch…...

Vue2学习笔记のVue组件化编程
目录 Vue组件化编程非单文件组件基本使用几个注意点组件的嵌套VueComponent一个重要的内置关系 单文件组件index.htmlmain.jsApp.vueSchool.vueStudent.vue 各位小伙伴们好呀,不知道上一篇文章你是否有收获!这篇是Vue2学习笔记第二篇,也是Vue…...

跨境电商儿童沙画办理EN71测试标准
儿童沙画就是小孩子玩的那种用彩色沙子或者彩色墨水,在有图形轮廓的纸片上去绘画,可以按照儿童沙画底板上的人物轮廓线条,动物线条,风景线条,动漫线条,去添加自己喜欢的颜色,让单调的线条变成自…...
chrome浏览器账号密码输入框自动填充时背景色不变
处理前 使用延时的方式解决 .login-box input,password:-webkit-autofill .login-box input,password:-webkit-autofill:hover, .login-box input,password:-webkit-autofill:focus, .login-box input,password:-webkit-autofill:active {-webkit-transition-delay: 999999…...
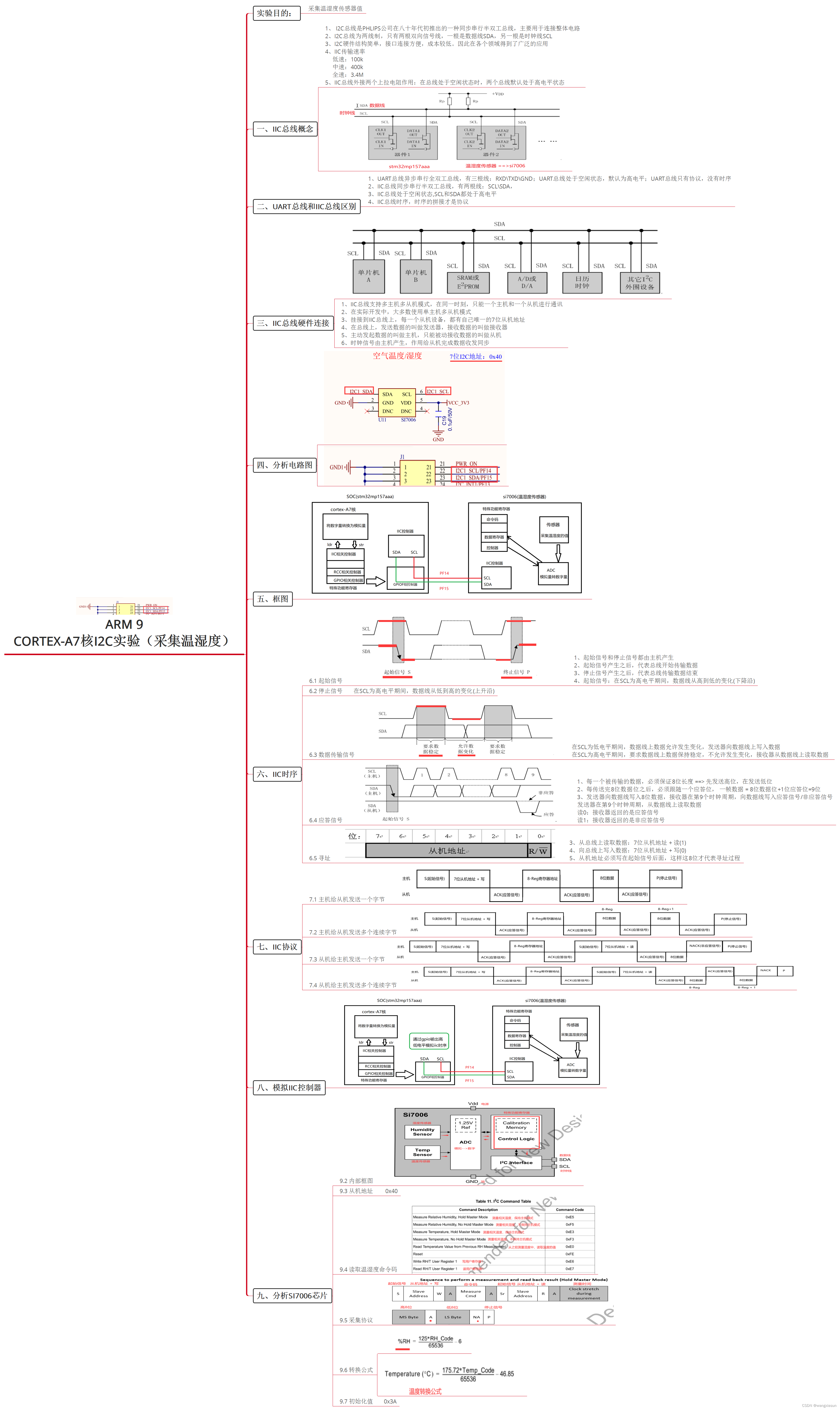
【ARM】Day9 cortex-A7核I2C实验(采集温湿度)
1. 2、编写IIC协议,采集温湿度值 iic.h #ifndef __IIC_H__ #define __IIC_H__ #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_rcc.h" #include "led.h" /* 通过程序模拟实现I2C总线的时序和协议* GPIOF ---> AHB4* I2C1_S…...
【Leetcode】移动零
移动零 题目描述算法描述编程代码 链接: 移动零 题目描述 算法描述 编程代码 class Solution { public:void moveZeroes(vector<int>& nums) {//题目要求不可以复制数组,开辟额外空间int dest -1,curr 0;for(;curr < nums.size();curr){if(nums[cu…...
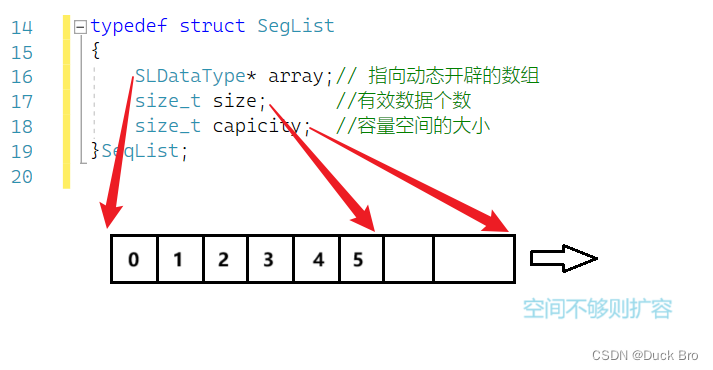
数据结构入门 — 顺序表详解
前言 数据结构入门 — 顺序表详解 博客主页链接:https://blog.csdn.net/m0_74014525 关注博主,后期持续更新系列文章 文章末尾有源码 *****感谢观看,希望对你有所帮助***** 文章目录 前言一、顺序表1. 顺序表是什么2. 优缺点 二、概念及结构…...

SimpleCG绘图函数(9)--绘制各种线条
一、所有线段函数概述 可填充图形绘制函数都介绍完了,还有一些特殊线条的绘制将在本篇进行讲解。所有特殊线条函数如下所示,其中还有一个区域填充函数floodfill比较特殊,是配合线条函数使用的: //绘制一系列折线段 //折线段以一组…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

