线性代数的学习和整理5: 矩阵的加减乘除及其几何意义
目录
1 矩阵加法
1.1 矩阵加法的定义
1.2 加法的属性
1.2.1 只有同类型,相同n*m的矩阵才可以相加
1.2.1 矩阵加法的可交换律:
1.2.2 矩阵加法的可结合律:
1.3矩阵加法的几何意义
2 矩阵的减法
2.1 矩阵减法定义和原理基本同 矩阵的加法
2.2 矩阵减法的几何意义
3 矩阵标量乘法/ 也称 数乘
3.1 数乘的定义
3.2 矩阵的标量乘法的性质
3.3 几何意义:就是 正向/反向的伸缩
4 左乘 & 右乘 (很简单概念,但是需要界定语言的严谨性)
4.1 搞清楚主体:谁的左乘?右乘?
4.2 搞清楚方向:什么是左乘和右乘
4.3 一般的线性代数公式 AX=Y, 表示 x 左乘矩阵A
5 矩阵的点乘:得到的点积/内积
5.1 详细的矩阵乘法规则
5.1.1 计算规则是:只有形如 n*m矩阵* m*k的矩阵的矩阵才可以相乘
5.1.2 矩阵的乘法不符合交换性,不能交换次序,左乘 ≠ 右乘,A*B ≠B*A
5.2 矩阵点乘法:得到的内积/点积的几何意义
6 矩阵的叉乘:得到的外积/叉积
6.1 定义
6.2 几何意义
7 矩阵求逆(逆矩阵)
7.1 逆矩阵定义
7.2 求逆矩阵的方法
7.3 求逆矩阵的规则
7.3.1 并不是所有的矩阵都可以求逆矩阵
7.4 逆矩阵的函数意义
7.5 逆矩阵的几何意义
8 带引号的“矩阵除法”
8.1 一般没有矩阵除法的说法,但可以这么理解
8.2 矩阵除法的几何意义(?)
1 矩阵加法
1.1 矩阵加法的定义
- 矩阵加法一般是指两个矩阵把其相对应元素加在一起的运算。

1.2 加法的属性
可结合律和可交换律
1.2.1 只有同类型,相同n*m的矩阵才可以相加
- (1,2)+(1,2,3) 无法计算
- 如何合法可加,生成的结果也是一个向量
1.2.1 矩阵加法的可交换律:
- A+B=B+A
- 看坐标系,表示从上面走先走b,再走a到达C,和从下面先走a,再走b到达C是一样的。
1.2.2 矩阵加法的可结合律:
- (A+B)+C=A+(B+C)
- 看坐标系,表示3个矩阵相加,先计算A+B,再计算A+B+C 和先计算B+C 结果是一样的。
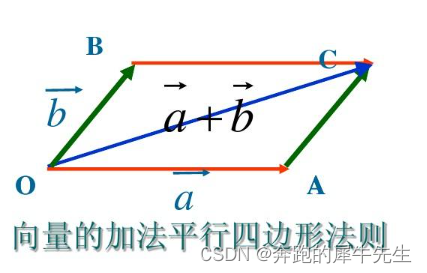
1.3矩阵加法的几何意义
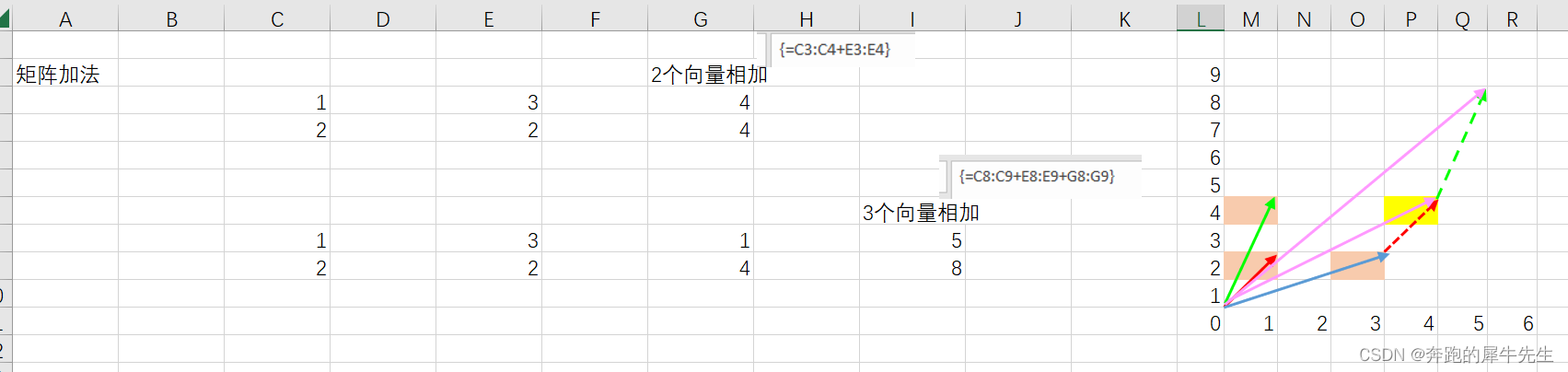
- 看下图,实际是向量的相加,是有方向性的,不是简单的相加
- 而无论2个,还是3个向量相加,都可以用三角形发展继续相加,生成的新向量就是矩阵相加的和----一个新向量


2 矩阵的减法
2.1 矩阵减法定义和原理基本同 矩阵的加法
- 虽然一般不说矩阵减法,但原理上OK,EXCEL里计算也OK

2.2 矩阵减法的几何意义
- 矩阵的减法和加法其实是类似的,但是几何意义不同
- 加法是2个向量,首尾相接,形成新的向量--和向量
- 减法是1个减数向量,开始指向另1个被减数的向量,形成的新向量:差向量。如可以可以挪到原点,从原点出发,
- 可以看出如下图,和从原点出发,而数字为减法后得数的终点作为坐标的向量,是相同的。
- 为什么一定要挪回到原点看,因为向量空间里要求所有的向量都是从原点出发,终点坐标代表其坐标的向量。


3 矩阵标量乘法/ 也称 数乘
3.1 数乘的定义
- λ*(A+B) =λ*A+λ*B
- 就是 标量*矩阵对应位置元素,类整数的乘法
3.2 矩阵的标量乘法的性质
- 可结合性:a*X={ax1,ax2,ax3.....axn]
- 可交换性: a*X=X*a
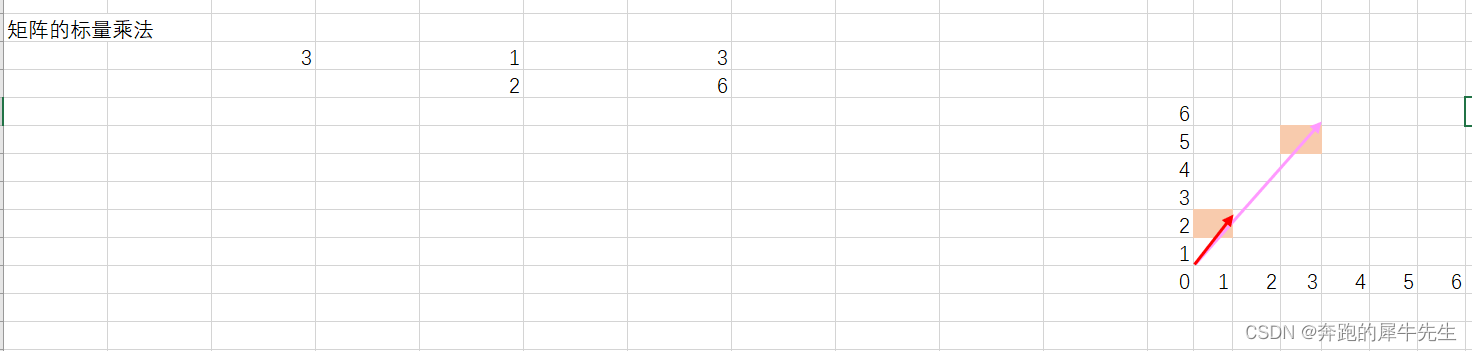
3.3 几何意义:就是 正向/反向的伸缩
- 如果乘以正数,就是正向伸缩
- 如果乘以负数,就是反向伸缩
- 如果乘以a>1,就是伸长,
- 如果a=0.5 就是缩短
4 左乘 & 右乘 (很简单概念,但是需要界定语言的严谨性)
4.1 搞清楚主体:谁的左乘?右乘?
- 比如 Ax=y
- 主体:变量? 那变量 x 左乘矩阵A
- 主题,矩阵? 那矩阵A 右乘变量x
4.2 搞清楚方向:什么是左乘和右乘
- A*B ≠ B*A
- A*B 是A右乘B, 是A的右边乘以B
- B*A 是A左乘B,是A的左边乘以B
4.3 一般的线性代数公式 AX=Y, 表示 x 左乘矩阵A
- 一般的线性代数公式 AX=Y, 表示 x 左乘矩阵A
5 矩阵的点乘:得到的点积/内积
- 在EXCEL里,使用函数 mmult()+ 选择好生成矩阵的长宽区域+数组公式
- 注意要提前计算好 目标矩阵的大小,比如 n*m矩阵* m*k的矩阵,结果是 m*k的矩阵

5.1 详细的矩阵乘法规则
5.1.1 计算规则是:只有形如 n*m矩阵* m*k的矩阵的矩阵才可以相乘
并不是任意2个矩阵都可以相乘
- 只有形如 n*m矩阵* m*k的矩阵的矩阵才可以相乘,也就是前者的列数=后者的行数
- aij= 矩阵1的第i行* 矩阵2的第j列的结果
本质规则
- 是两个矩阵元素的投射形成的新矩阵
5.1.2 矩阵的乘法不符合交换性,不能交换次序,左乘 ≠ 右乘,A*B ≠B*A
- 矩阵乘法要详细考虑次序,不能交换
- A*B ≠ B*A
- 矩阵乘法的具体公式:需要考虑展开,后面详细再说
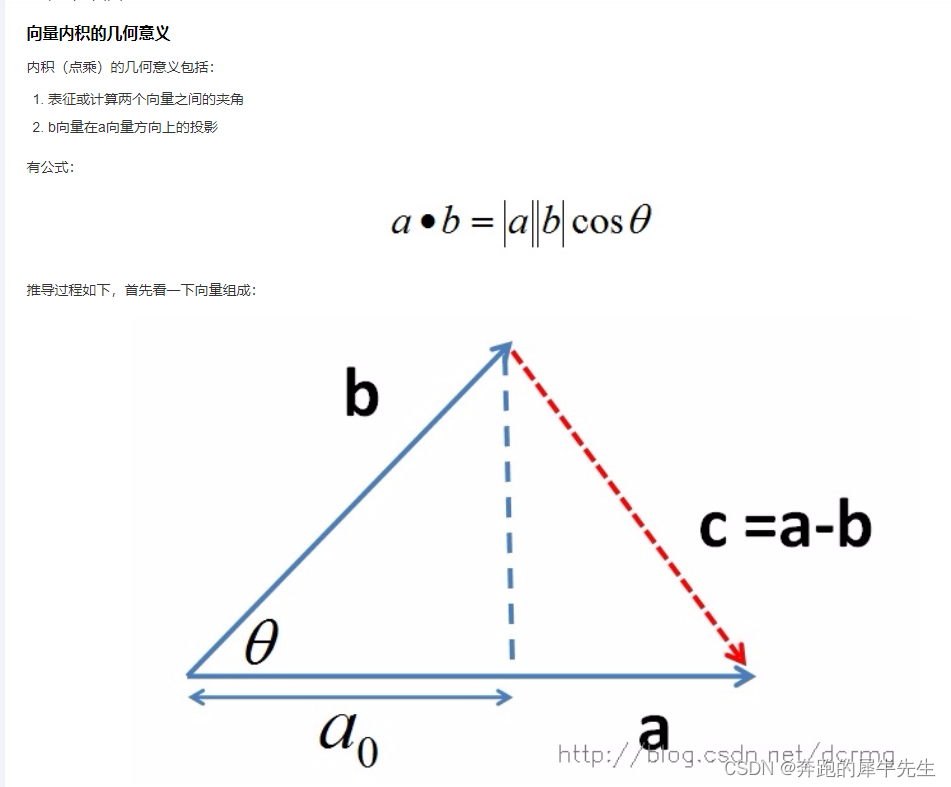
5.2 矩阵点乘法:得到的内积/点积的几何意义
- 矩阵的内积得到的是一个标量,也就是具体的数,而不是矩阵。
- 下图是网上找的
- 向量的内,外积及其几何含义讲解_两向量外积的几何意义-腾讯云开发者社区-腾讯云概括地说,向量的内积(点乘/数量积)。对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作,如下所示,对于向量a和向量b:
 https://cloud.tencent.com/developer/article/2157496
https://cloud.tencent.com/developer/article/2157496

6 矩阵的叉乘/向量乘法:得到的外积/叉积
6.1 定义
- 没学过,还不太清楚,下面是转载的外积的内容
- 有点像把矩阵的每个元素,当成一个分块矩阵,分别与另外一个矩阵相乘
- 得到的结果是一个矩阵


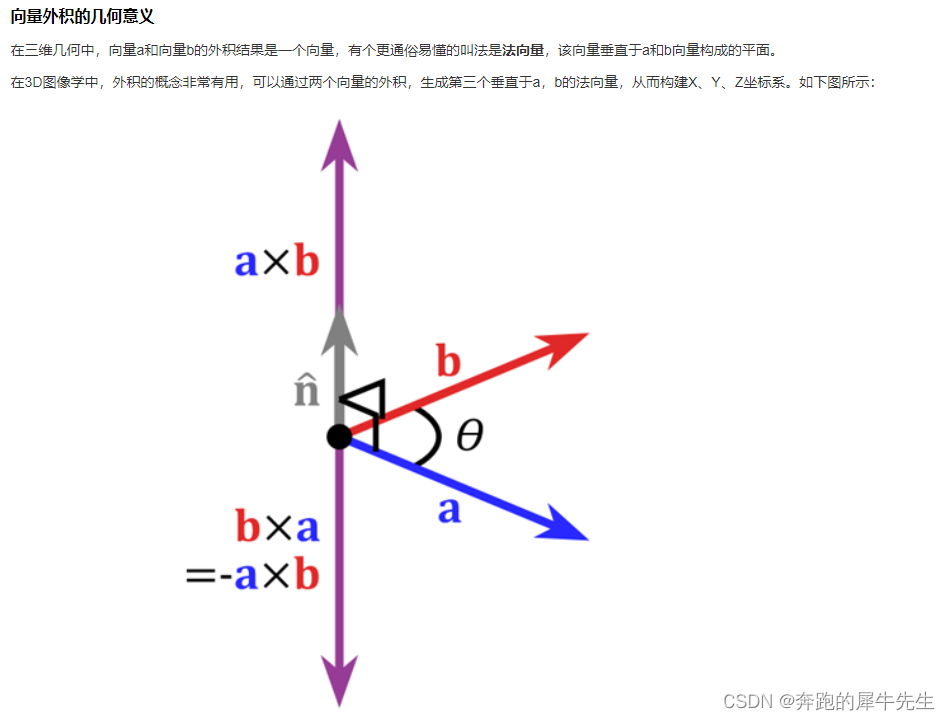
6.2 几何意义
- 据说,2个向量的外积表现为这2个向量所构成的平行六面体的体积!
7 矩阵求逆(逆矩阵)
7.1 逆矩阵定义
- 矩阵A为n阶方阵,若存在n阶矩阵B,使得矩阵A、B的乘积为单位阵,则称A为可逆阵,B为A的逆矩阵。A*B=I/E
- 若方阵的逆阵存在,则称为可逆矩阵或非奇异矩阵,且其逆矩阵唯一。
- 逆矩阵比然唯一
7.2 求逆矩阵的方法
- 主要是利用 A*A-=I 标准矩阵

7.3 求逆矩阵的规则
7.3.1 并不是所有的矩阵都可以求逆矩阵
- 并不是所有的矩阵都可以求逆矩阵
- 特殊条件是:
- 方阵
- 满秩的
- 双射矩阵
满足这些条件的矩阵才可以求逆
7.3.2 比较方便的快速判断方法,判断标准如下
- 如果矩阵的行列式值是否为0,若不为0,则可逆;
- 看这个矩阵的秩是否为n,若为n,则矩阵可逆;如果小于n,不可逆。
- 若存在一个矩阵B,使矩阵A使得AB=BA=E,则矩阵A可逆;
- 对于齐次线性方程AX=0,若方程只有零解,那么这个矩阵可逆;
- 对于非齐次线性方程AX=b,若方程只有特解,那么这个矩阵可逆,反之若有无穷解则矩阵不可逆。
7.4 逆矩阵的函数意义
- 如果把矩阵看成函数
- 那么函数,只有当定义域到值域是单射,且值域都是满射时,也就是定义域到值域是双射时才会有反函数
- 同理,也只有这时,矩阵才会有逆矩阵。
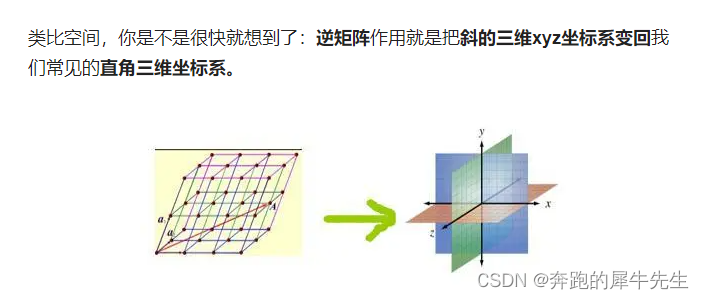
7.5 逆矩阵的几何意义
- 常见矩阵乘法 Ax=y,可以认为是把x从自然基底(正交的一组特殊基底)变换为斜的新坐标系。
- 那么,逆矩阵就是反过来,把斜坐标系再给转换为正交的自然基底。
百度安全验证https://baijiahao.baidu.com/s?id=1731151185141060114&wfr=spider&for=pc
8 带引号的“矩阵除法”
8.1 一般没有矩阵除法的说法,但可以这么理解
- 这个除法实际只是一个类比,并不是真正的 矩阵除法!
这个题目的意思是:
如果知道 ,A矩阵*B矩阵=C矩阵
但是A矩阵已知,C矩阵也已知,如何求B矩阵?
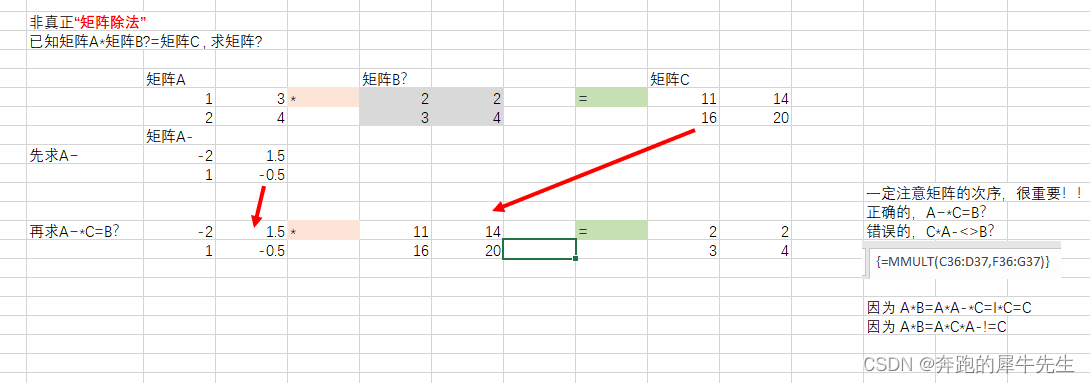
A矩阵*B?矩阵=C矩阵
A*B?=C 那么B?=? 其实B=A-*C 而不是C*A-
- 一定注意矩阵的次序,很重要!!
- 正确的,B=A~*C,而且B !=C*A-
- 错误的,B =C*A-
- 因为如下推导
- A*B= A*A-*C =I*C=C
- A*B= A*C*A- !=C
8.2 矩阵除法的几何意义(?)
- 这个应该就是函数变换吧,暂时不知道其几何意义是什么
- A*B= A*A-*C =I*C=C
- B=A-*C
相关文章:

线性代数的学习和整理5: 矩阵的加减乘除及其几何意义
目录 1 矩阵加法 1.1 矩阵加法的定义 1.2 加法的属性 1.2.1 只有同类型,相同n*m的矩阵才可以相加 1.2.1 矩阵加法的可交换律: 1.2.2 矩阵加法的可结合律: 1.3矩阵加法的几何意义 2 矩阵的减法 2.1 矩阵减法定义和原理基本同 矩阵的…...

sqlsugar 使用TNS连接oracle
在使用SqlSugar连接Oracle数据库时,可以通过TNS来实现连接。以下是一个示例代码,展示了如何使用TNS连接Oracle数据库: 首先,确保您已经安装了Oracle客户端,并正确配置了TNS的相关信息。 // 引入SqlSugar命名空间 usi…...

用python解压zip文件
因为某个需求,需要用python处理解压文件,这里记录下完成的代码,需要注意的是删除解压出来的文件夹时,很多博客都说直接用removedirs就行,实际我在py3.7上测试会提示“文件夹非空”,而且想想如果直接移除了根…...

代码随想录22| 216.组合总和III, 17.电话号码的字母组合
216.组合总和III 题目链接/文章讲解:链接地址 视频讲解:链接地址 代码思路:回溯三部曲: 1.确定函数参数:n,k,sum,startIndex; 2.结束条件,path k,并且如果sumn 结束递归 3.递归回溯逻辑。 class Solution…...

ITIL4—战略与指导
战略与指导 成功的服务提供,需要朝着商定的目标采取协调一致的行动。本节将探讨服务供应商战略的创建和管理,其目的是首先对战略的本质、范围,以及战略与指导的关系建立基本的理解,然后为与该战略一致的指导活动提供指导。 本节…...
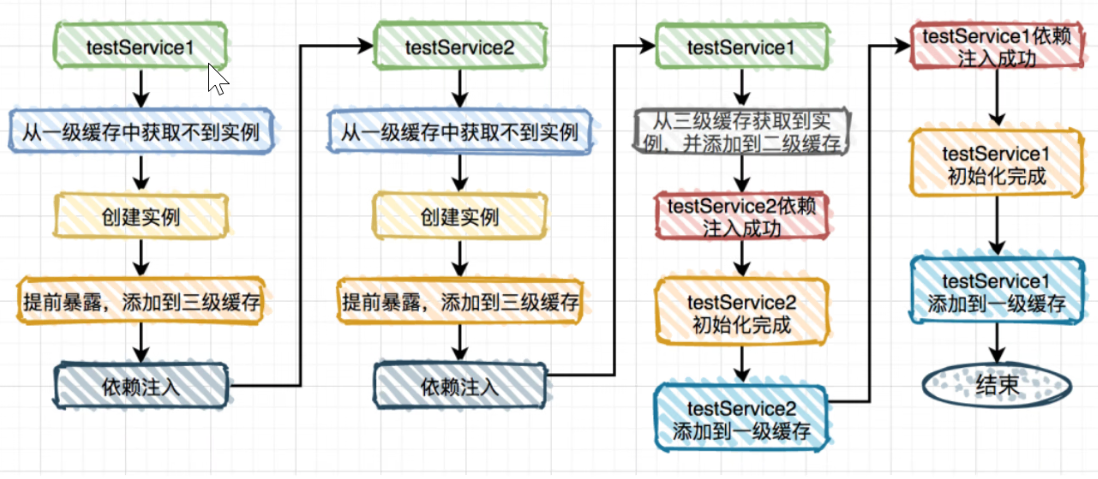
【Spring】Spring循环依赖(超重要!!)
目录 什么是循环依赖问题 循环依赖具体是怎么解决的 具体的解决步骤: 通俗实例: 严谨的循环依赖解决图例 为什么使用的是三级缓存,二级缓存不够用吗? 什么是循环依赖问题 Spring的循环依赖是指在Bean之间存在相互依赖关…...

数据分析之路应该是就此开启了
咱就是说工作以后,就是重新学习的开始啊。 祝自己顺顺利利。 前路漫漫亦灿灿。 数据分析之路,开启吧。 以下是借鉴网上的学习路线。 这个学习路线图主要分为以下几个部分: 基础知识 :包括数学、统计学和编程语言。这是数据分析的…...
win10如何配置jdk环境变量
1.首先要打开系统环境变量配置的页面。具体操作是:打开开始菜单,找到“此电脑”,然后右键“更多”→“属性”。 2.在弹出的页面,选择“高级系统设置” 3.在弹出的页面,选择“环境变量(N)…”。 …...

pm4py使用指南(非机翻)
目录 1. 日志数据读取及预处理(1)查看case和event数量(2)查看起始事件和结束事件(3)时间戳格式的问题 2. 日志数据过滤3. 流程发现4. 模型转化5. 模型可视化 1. 日志数据读取及预处理 通过 pandas库 读取c…...

ChatGPT帮助提升工作效率和质量:完成时间下降40%,质量评分上升 18%
自ChatGPT去年11月发布以来,人们就开始使用它来协助工作,热心的用户利用它帮助撰写各种内容,从宣传材料到沟通话术再到调研报告。 两名MIT经济学研究生近日在《科学》杂志上发表的一项新研究表明,ChatGPT可能有助于减少员工之…...

第二章 搜索
本篇博文是笔者归纳汇总的AcWing基础课题集,方便读者后期复盘巩固~ PS:本篇文章只给出完整的算法实现,并没有讲解具体的算法思路。如果想看算法思路,可以阅读笔者往期写过的文章(或许会有),也可…...

transform_train.json文件解析
transform_train.json 文件内容解析transform_matrix 文件内容解析 {"camera_angle_x": 0.6911112070083618,"frames": [{"file_path": "./train/r_0","rotation": 0.012566370614359171,"transform_matrix": [[…...
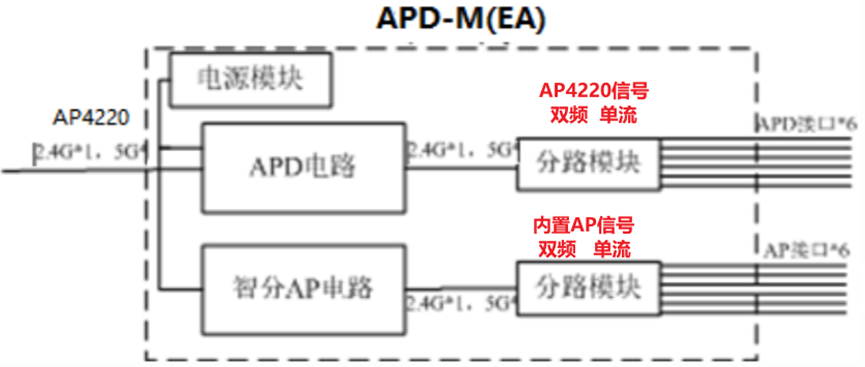
Wlan——锐捷零漫游网络解决方案以及相关配置
目录 零漫游介绍 一代零漫游 二代单频率零漫游 二代双频率零漫游 锐捷零漫游方案总结 锐捷零漫游方案的配置 配置无线信号的信道 开启关闭5G零漫游 查看配置 零漫游介绍 普通的漫游和零漫游的区别 普通漫游 漫游是由一个AP到另一个AP或者一个射频卡到另一个射频卡的漫…...

分布式锁系列之zookeeper分布式锁和mysql分布式锁
目录 介绍 下载安装 基本指令编辑 java集成zookeeper 官方提供版 永久节点 临时节点编辑 永久序列化节点 判断当前节点是否存在 获取当前节点中的数据内容 获取当前节点的子节点 更新节点内容 删除节点 zookeeper实现分布式锁 Mysql实现分布式锁 总结 介绍 ZooK…...

Ubuntu部署PHP7.4
系统版本:Ubuntu22.04 PHP版本: 7.4 Mysql版本:8.0 Nginx版本: 最新 1. 更新系统 首先,确保系统包是最新的: sudo apt update && sudo apt upgrade -y2. 安装 Nginx Nginx 在默认的 Ubuntu 仓库中,因此安装…...
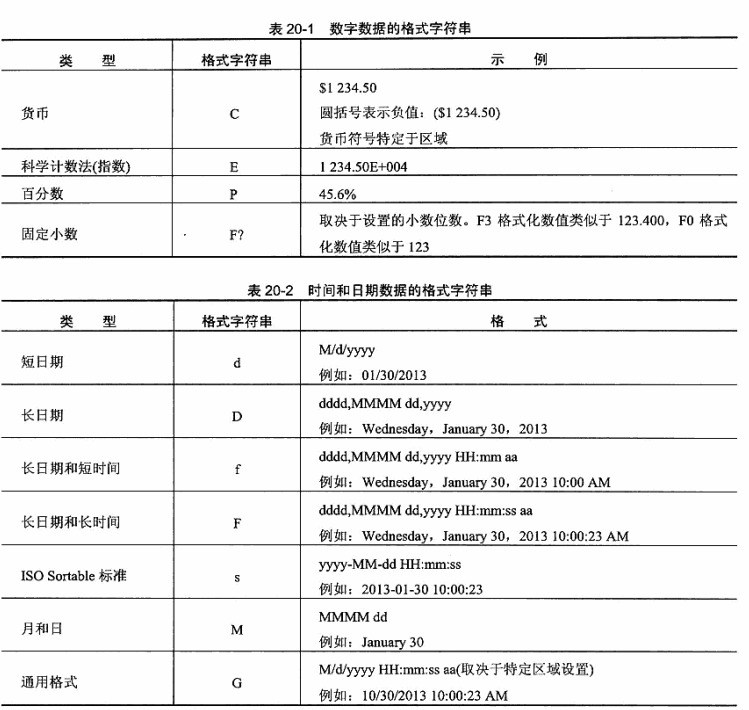
WPF中的数据转换-StringFormat
WPF中的数据转换-StringFormat 前言 字符串格式化。使用该功能可以通过设置Binding.StringFormat属性对文本形式的数据进行转换——例如包含日期和数字的字符串。对于至少一半的格式化任务,字符串格式化是一种便捷的技术。 使用 当设置Binding.StringFormat属性…...

java.lang.UnsupportedOperationException解决方法
java.lang.UnsupportedOperationException解决方法 先放错误信息业务场景报错分析先看报错代码位置进入源码查看至此 真相大白 解决方法总结 先放错误信息 业务场景 已知有学生 张三李四王五赵六 等人 private List<String> nameList Arrays.asList("张三", &…...
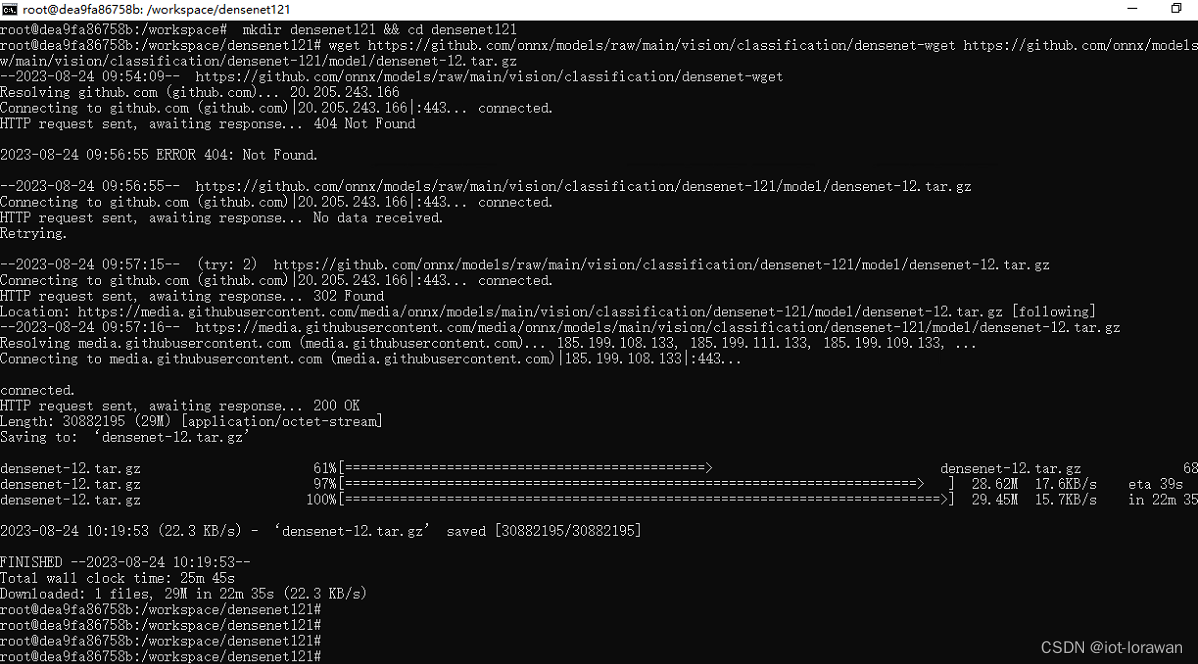
docker for window更改到非系统盘的使用记录
1、使用Hyper-v模式的docker安装 2、安装docker for windows后安装目录没办法自己选择,固定在c盘 卸载后通过命令行方式设置软连接方式后重新安装来让其安装到软连接的d盘,解决c盘空间问题 mklink /j "C:\Program Files\Docker" "D:\Pr…...

day 38 | ● 518. 零钱兑换 II ● 377. 组合总和 Ⅳ
518. 零钱兑换 II 这道题就是完全背包问题,因为可以选择的数量是无限的。所以第二层的遍历顺序就是从前往后。 因为是次数问题,递推公式是 的,初值应该设定为dp【0】 1,否则无法进行累加。 func change(amount int, coins []i…...

写得了代码,焊得了板!嵌入式开发工程师必修之代码管理方案(中)
目录 2.2 分仓、权限与依赖问题 2.3 基于 Git 进行多仓管理 Git submodule Git subtree Script/CMake Git-Repo Conan 本文来自 武让 极狐GitLab 高级解决方案架构师 🌟 前一篇文章,作者介绍了嵌入式开发场景的代码管理特点与诉求,以及…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
