GAN:对抗生成网络,前向传播和后巷传播的区别
目录
GAN:对抗生成网络
损失函数
判别器开始波动很大,先调整判别器
生成样本和真实样本的统一:真假难辨编辑
文字专图片编辑
头像转表情包编辑
头像转3D编辑
后向传播
1. 前向传播(forward)
2. 反向传播(backward):得到权重参数公式,寻找优路径
反向传播的四个基本方程
链式法则误差求和
梯度下降权重参数更新编辑
GAN:对抗生成网络




损失函数


判别器开始波动很大,先调整判别器


生成样本和真实样本的统一:真假难辨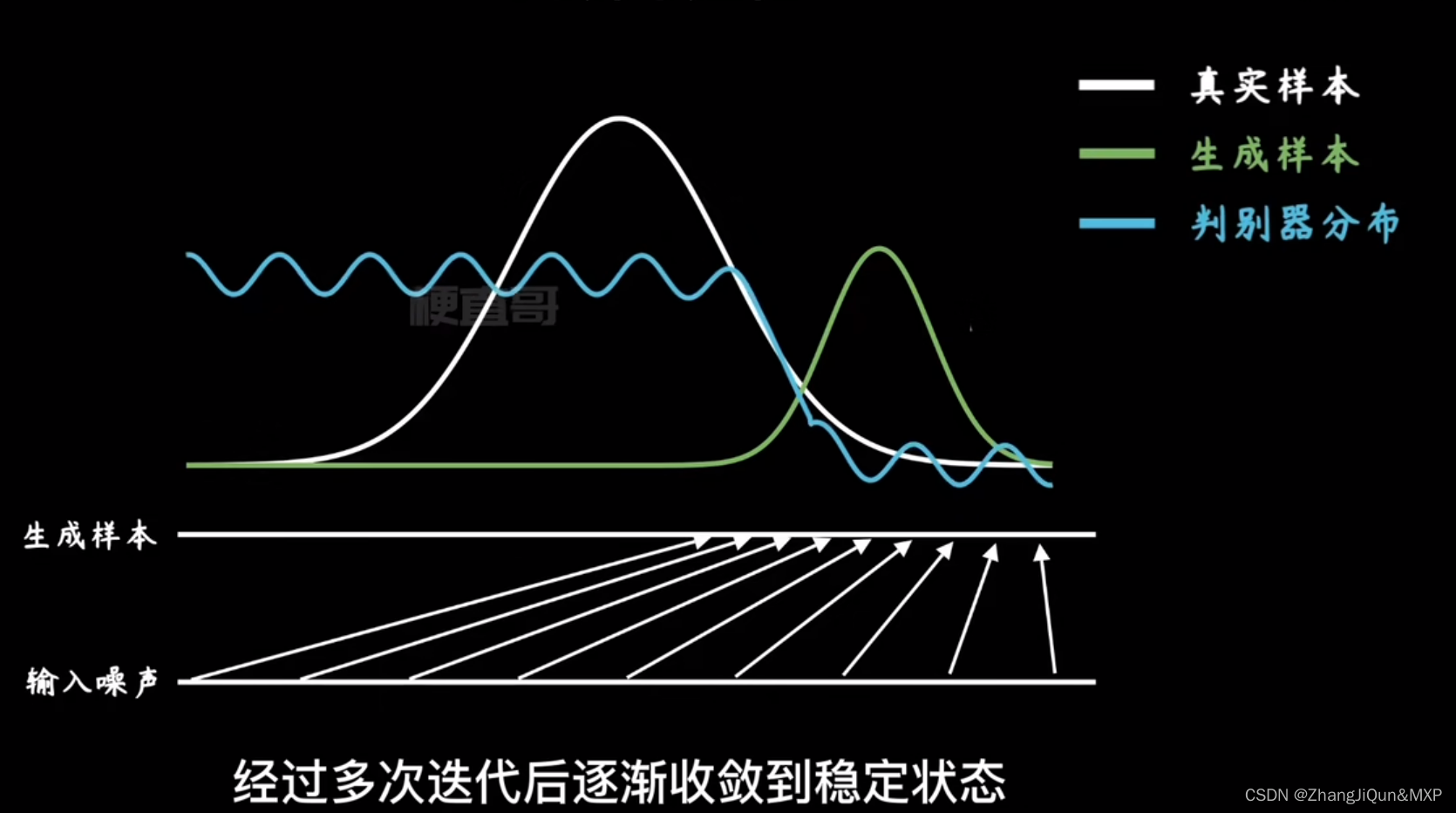

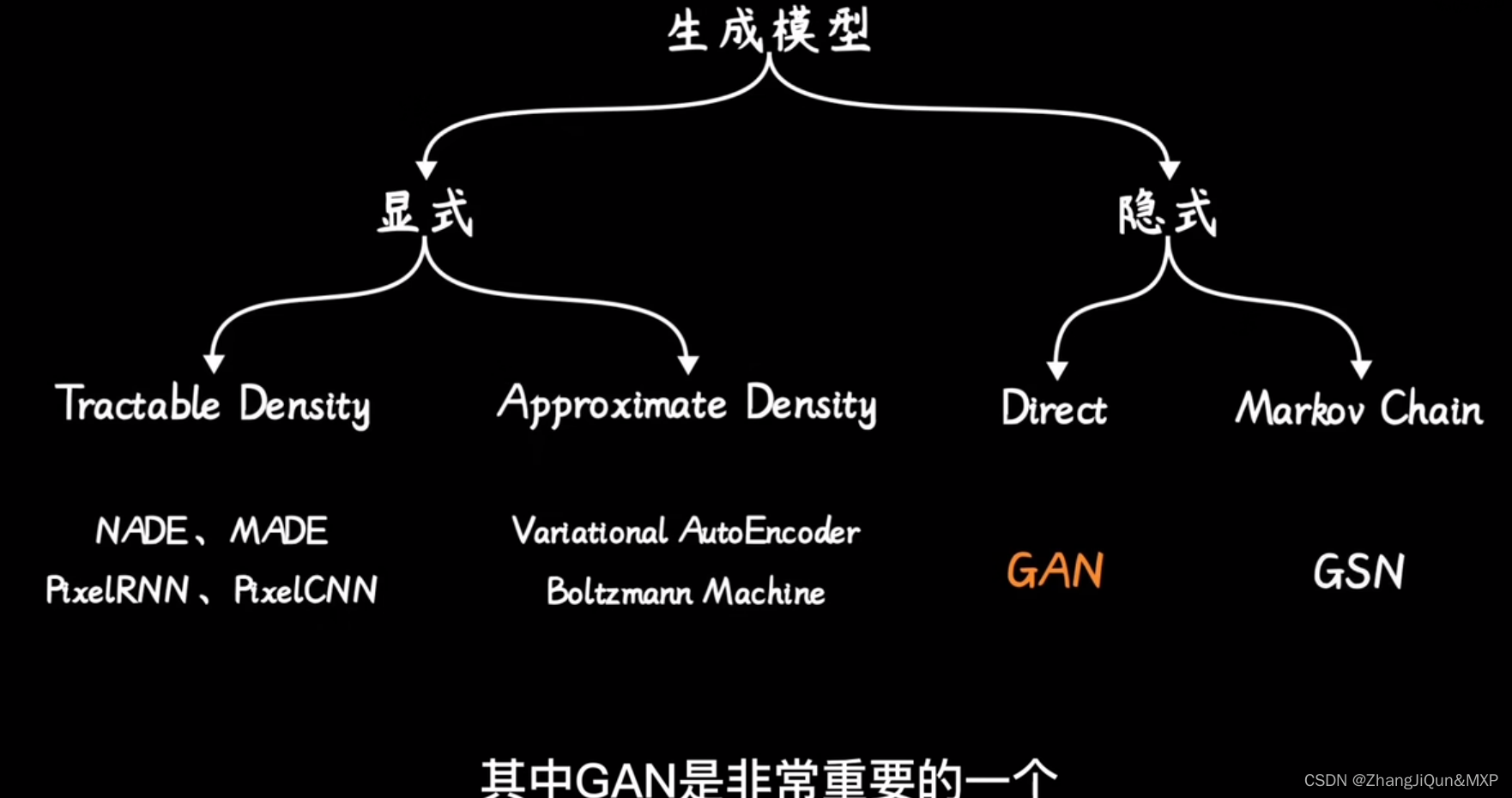
图像数据集生成

文字专图片
头像转表情包
头像转3D

贝叶斯:后验
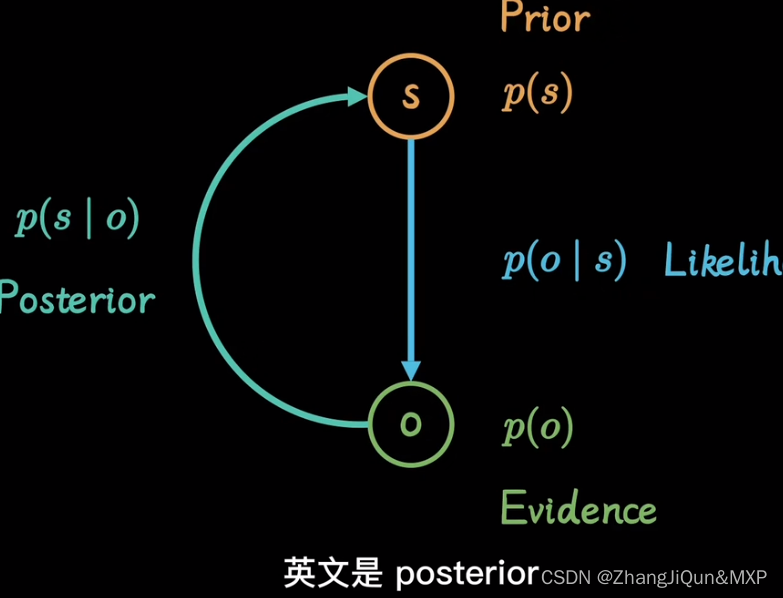


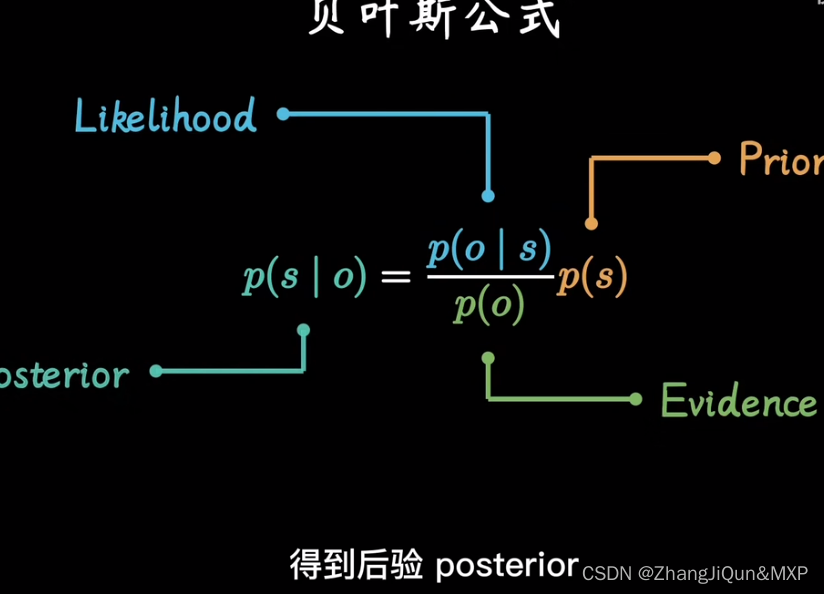

后向传播
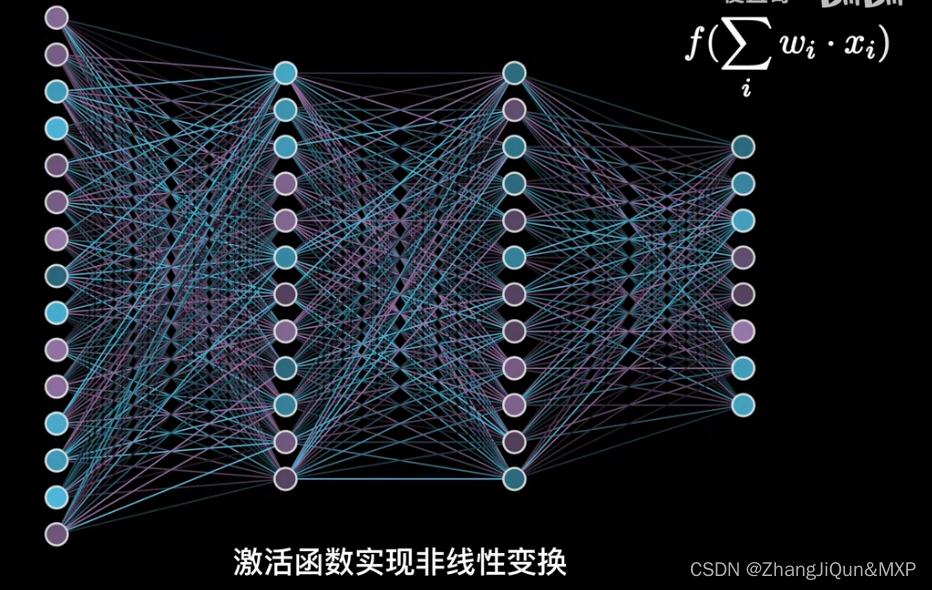

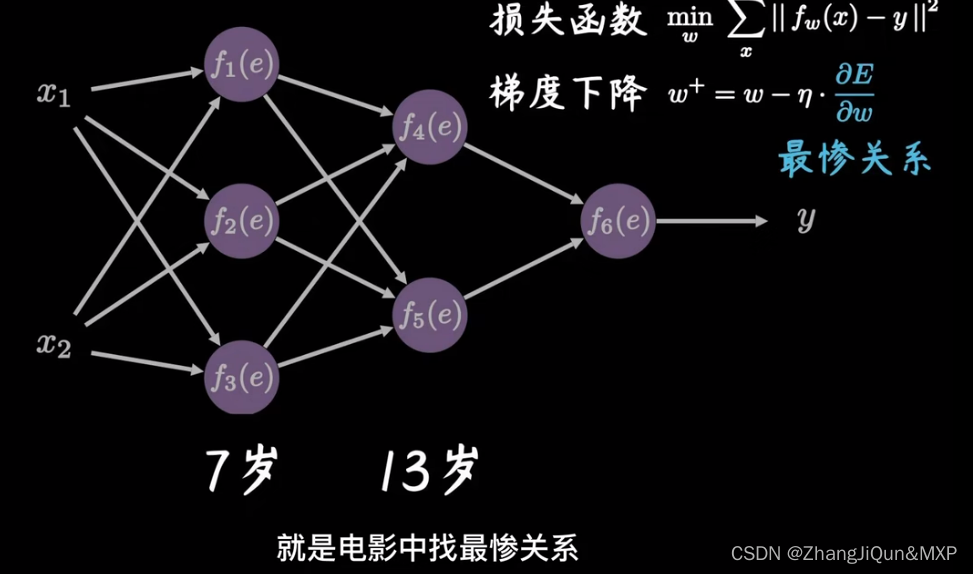
前向传播:通过输入层输入,一路向前,通过输出层输出的一个结果。如图指的是1 、 x1、x2、xn、与权重(weights)相乘,并且加上偏置值b0,然后进行总的求和,同时通过激活函数激活之后算出结果。这个过程就是前向传播。
反向传播:通过输出反向更新权重的过程。具体的说输出位置会产生一个模型的输出,通过这个输出以及原数据计算一个差值。将前向计算过程反过来计算。通过差值和学习率更新权重。
1. 前向传播(forward)
简单理解就是将上一层的输出作为下一层的输入,并计算下一层的输出,一直到运算到输出层为止。接下来我们用数学公式描述一下:

权重

偏置
设 wjkl 为 l−1 层第 k 个神经元到第 l 层第 j 个神经元的weight, bjl 为第 l 层第 j 个神经元的bias, ajl 为第第 l 层第 j 个神经元的激活值(激活函数的输出,保证模型的非线性)。
对于Layer 2的输出 a1(2) ,a2(2),a3(2),
a1(2)=σ(z1(2))=σ(w11(2)x1+w12(2)x2+w13(2)x3+b1(2))
a2(2)=σ(z2(2))=σ(w21(2)x1+w22(2)x2+w23(2)x3+b2(2))
a3(2)=σ(z3(2))=σ(w31(2)x1+w32(2)x2+w33(2)x3+b3(2))
对于Layer 3的输出a1(3),
a1(3)=σ(z1(3))=σ(w11(3)a1(2)+w12(3)a2(2)+w13(3)a3(2)+b1(3))
a2(3)=σ(z2(3))=σ(w21(3)a1(2)+w22(3)a2(2)+w23(3)a3(2)+b2(3))
从上面可以看出,使用代数法一个个的表示输出比较复杂,而如果使用矩阵法则比较的简洁。将上面的例子一般化,并写成矩阵乘法的形式,
z(l)=W(l)a(l−1)+b(l)
a(l)=σ(z(l))
其中 σ 为 激活函数,如Sigmoid,ReLU,PReLU等。
2. 反向传播(backward):得到权重参数公式,寻找优路径
实际上,反向传播仅指用于计算梯度的方法。而另一种算法,例如随机梯度下降法,才是使用该梯度来进行学习。原则上反向传播可以计算任何函数的到导数。
在了解反向传播算法之前,我们先简单介绍一下链式法则:
微积分中的链式法则(为了不与概率中的链式法则相混淆)用于计复合函数的导数。反向传播是一种计算链式法则的算法,使用高效的特定运输顺序。
设 x 是实数, f 和 g 是从实数映射到实数的函数。假设 y=g(x) 并且 z=f(g(x))=f(y) 。那么链式法则就是: dzdx=dzdydydx 。
反向传播算法的核心是代价函数 C 对网络中参数(各层的权重 W 和偏置 b )的偏导表达式 ∂C∂W 和∂C∂b。这些表达式描述了代价函数值C随权重W或偏置b变化而变化的程度。BP算法的简单理解:如果当前代价函数值距离预期值较远,那么我们通过调整权重W或偏置b的值使新的代价函数值更接近预期值(和预期值相差越大,则权重W或偏置b调整的幅度就越大)。一直重复该过程,直到最终的代价函数值在误差范围内,则算法停止。
BP算法可以告诉我们神经网络在每次迭代中,网络的参数是如何变化的,理解这个过程对于我们分析网络性能或优化过程是非常有帮助的,所以还是尽可能搞透这个点。
反向传播过程中要计算偏导表达式 ∂C/∂W 和∂C/∂b,我们先对代价函数做两个假设,以二次损失函数为例:
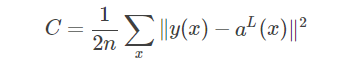
其中 n 为训练样本 x 的总数, y=y(x) 为期望的输出,即ground truth, L 为网络的层数, aL(x) 为网络的输出向量。
假设1:总的代价函数可以表示为单个样本的代价函数之和的平均:

这个假设的意义在于,因为反向传播过程中我们只能计算单个训练样本的∂Cx/∂Wx 和∂C/∂b,在这个假设下,我们可以通过计算所有样本的平均来得到总体的∂C/∂W 和∂C/∂b。
假设2:代价函数可以表达为网络输出的函数 Loss=C(aL) ,比如单个样本 x 的二次代价函数可以写为:
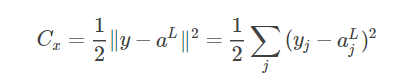
反向传播的四个基本方程
权重W或偏置b的改变如何影响代价函数 C 是理解反向传播的关键。最终,这意味着我们需要计算出每个的∂C/∂Wjkl 和∂C/∂bjkl,在讨论基本方程之前,我们引入误差 δ 的概念,δjl表示第 l 层第 j 个神经元的误差。
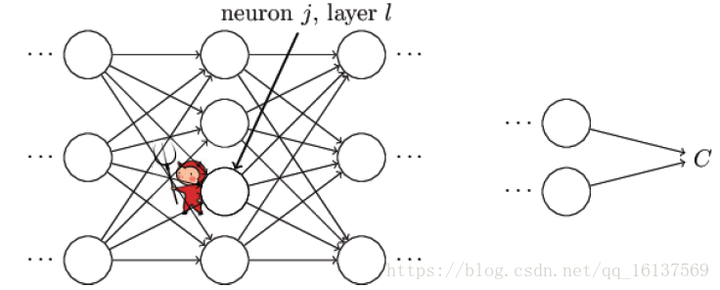
如上图所示,假设有个小恶魔在第 l 层第 j 个神经元捣蛋,他让这个神经元的权重输出变化了 Δzjl ,那么这个神经元的激活输出为 δ(zjl+Δzjl) ,然后这个误差向后逐层传播下去,导致最终的代价函数变化了 ∂C/∂zjlΔzjl 。现在这个小恶魔改过自新,它想帮助我们尽可能减小代价函数的值(使网络输出更符合预期)。假设 ∂C∂zjl 一开始是个很大的正值或者负值,小恶魔通过选择一个和 ∂C/∂zjl 方向相反的Δzjl使代价函数更小(这就是我们熟知的梯度下降法)。随着迭代的进行, ∂C/∂zjl 会逐渐趋向于0,那么Δzjl对于代价函数的改进效果就微乎其微了,这时小恶魔就一脸骄傲的告诉你:“俺已经找到了最优解了(局部最优)”。这启发我们可以用 ∂C/∂zjl 来衡量神经元的误差: δjl=∂C∂zjl 。
下面就来看看四个基本方程是怎么来的。
1. 输出层的误差方程

果上面的东西你看明白了,这个方程应该不难理解,等式右边第一项 ∂C∂ajL 衡量了代价函数随网络最终输出的变化快慢,而第二项 σ(1)(zjL) 则衡量了激活函数输出随 zjL 的变化快慢。当激活函数饱和,即 σ(1)(zjL)≈0 时,无论∂C∂ajL多大,最终 δjL≈0 ,输出神经元进入饱和区,停止学习。
方程中两项都很容易计算,如果代价函数为二次代价函数:
![]()
可以得到:
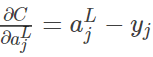
同理,对激活函数 σ(z) 求 zjL 的偏导即可求得 σ(1)(zjL) ,将它重写为矩阵形式:
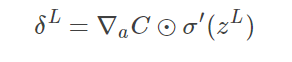
⊙ 为Hadamard积,即矩阵的点积。
链式法则误差求和

梯度下降权重参数更新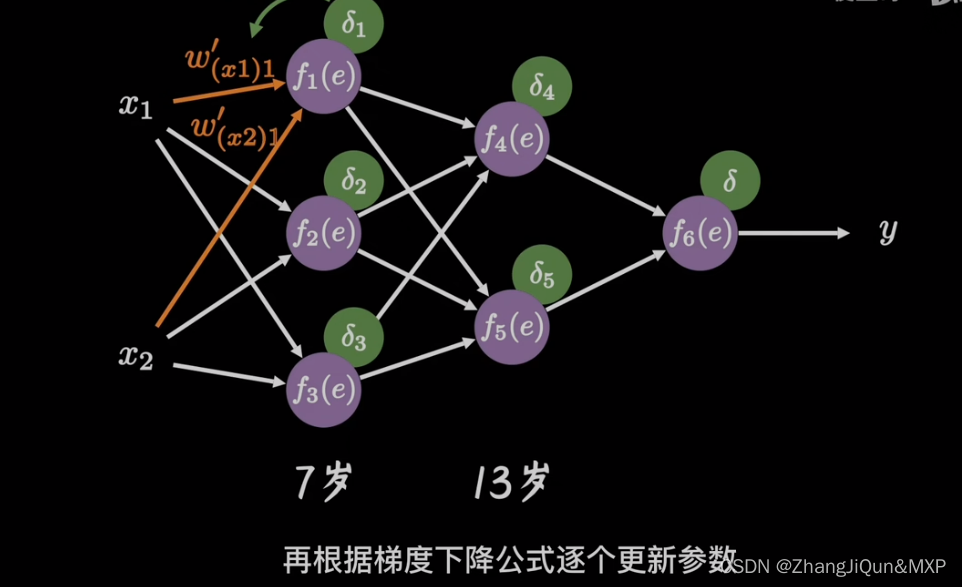
相关文章:

GAN:对抗生成网络,前向传播和后巷传播的区别
目录 GAN:对抗生成网络 损失函数 判别器开始波动很大,先调整判别器 生成样本和真实样本的统一:真假难辨编辑 文字专图片编辑 头像转表情包编辑 头像转3D编辑 后向传播 1. 前向传播(forward) 2. 反向传播&…...

压力变送器的功能与应用
压力变送器是用于测量气体或者液体等介质压力的设备,能够将压力转化为4 G信号传输到监控平台,工作人员可以在电脑或者手机上登录平台查看监测到的数据,并根据数据制定下一步的计划。 压力变送器的功能: 压力变送器采用了高性能感…...
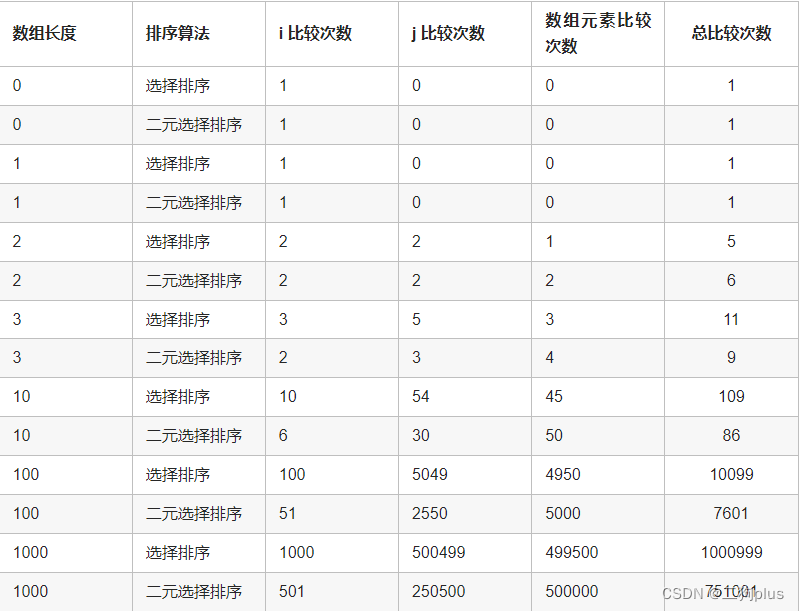
排序算法:选择排序
选择排序的思想是:双重循环遍历数组,每经过一轮比较,找到最小元素的下标,将其交换至首位。 public static void selectionSort(int[] arr) {int minIndex;for (int i 0; i < arr.length - 1; i) {minIndex i;for (int j i …...

Windows运行Spark所需的Hadoop安装
解压文件 复制bin目录 找到winutils-master文件hadoop对应的bin目录版本 全部复制替换掉hadoop的bin目录文件 复制hadoop.dll文件 将bin目录下的hadoop.dll文件复制到System32目录下 配置环境变量 修改hadoop-env.cmd配置文件 注意jdk装在非C盘则完全没问题,如果装在…...

KusionStack使用文档
下载安装 1. 安装 Kusionup 如果想自定义默认安装版本,可以运行下述命令(将最后的 openlatest 替换为你想要默认安装的版本号就就行): curl -s "http://kusion-public.oss-cn-hzfinance.aliyuncs.com/cli/kusionup/script…...
ONLYOFFICE 文档如何与 Alfresco 进行集成
ONLYOFFICE 文档是一款开源办公套件,其是包含文本文档、电子表格、演示文稿、数字表单、PDF 查看器和转换工具的协作性编辑工具。要在 Alfresco 中使用 ONLYOFFICE 协作功能,可以将他们连接集成。阅读本文,了解这如何实现。 关于 ONLYOFFICE…...
PostgreSQL下载路径与安装步骤
PgSQL介绍 PgSQL和MySQL一样是一种关系模型的数据库,全称为PostgreSQL 数据库。 优势:PgSQL是一种可扩展、可靠、可定制的数据库管理系统,具有良好的数据完整性和安全性,支持多种操作系统,包括 Linux、Windows、MacOS …...

如何在PHP中编写条件语句
引言 决策是生活不可缺少的一部分。从平凡的着装决定,到改变人生的工作和家庭决定。在开发中也是如此。要让程序做任何有用的事情,它必须能够对某种输入做出响应。当用户点击网站上的联系人按钮时,他们希望被带到联系人页面。如果什么都没有…...
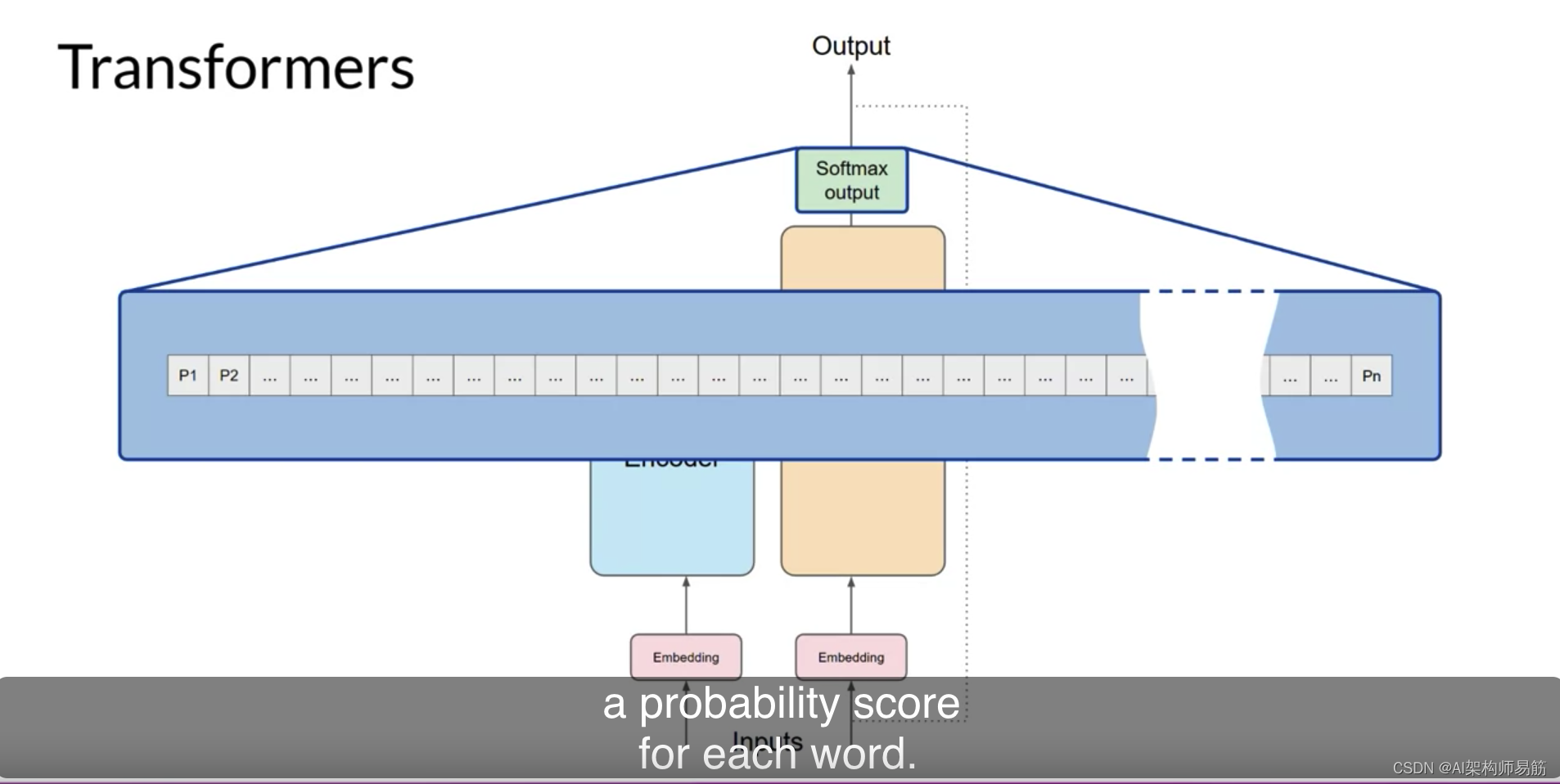
LLM架构自注意力机制Transformers architecture Attention is all you need
使用Transformers架构构建大型语言模型显著提高了自然语言任务的性能,超过了之前的RNNs,并导致了再生能力的爆炸。 Transformers架构的力量在于其学习句子中所有单词的相关性和上下文的能力。不仅仅是您在这里看到的,与它的邻居每个词相邻&…...
计算机网络 QA
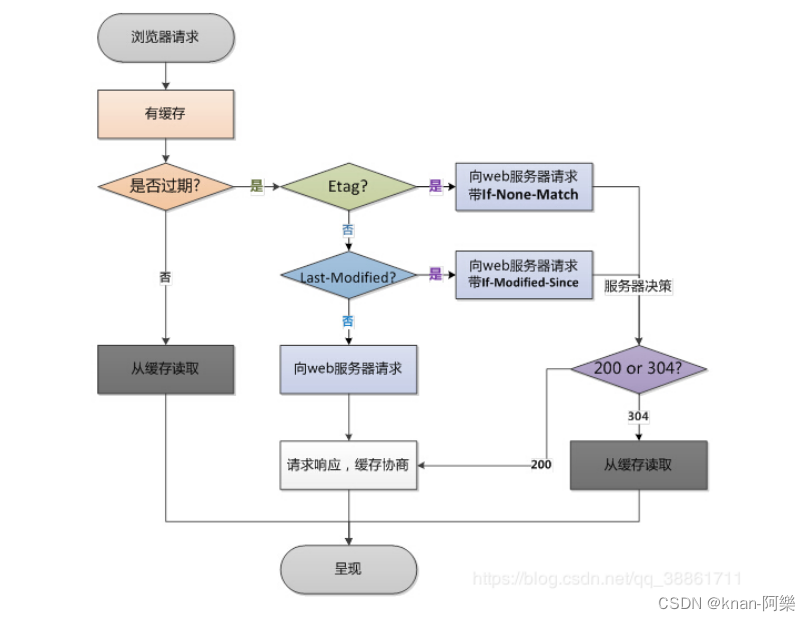
DNS 的解析过程 浏览器缓存。当用户通过浏览器访问某域名时,浏览器首先会在自己的缓存中查找是否有该域名对应的 IP 地址(曾经访问过该域名并且没有清空缓存)系统缓存。当浏览器缓存中无域名对应的 IP 地址时,会自动检测用户计算机…...
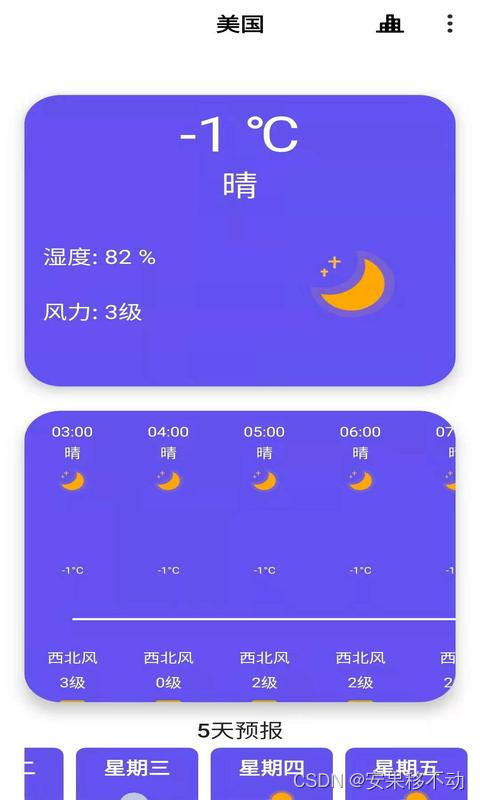
安果天气预报 产品介绍
软件介绍版本号 2.0.5 安果天气预报:全世界覆盖,中国定制 想要查找北京、上海、纽约、东京还是巴黎的天气?一款简约的天气预 报应用为你呈现。专注于为用户提供纯净的天气体验,我们不发送任何打扰的通知。包含空气质量、能见度、…...
net start Mysql 启动服务时 ,显示“Mysql服务正在启动 Mysql服务无法启动 服务没有报告任何错误
一、问题 有时候,输入net start Mysql 启动服务时 mysql>net start Mysql 显示 Mysql服务正在启动 Mysql服务无法启动 服务没有报告任何错误 二、原因 由于mysql的默认端口是3306,因此在启动服务的时候,如果此端口被占用,就会出…...

DAY24
题目一 啊 看着挺复杂 其实很简单 第一种方法 就是纵轴是怪兽编号 横轴是能力值 看看能不能打过 逻辑很简单 看看能不能打得过 打过的就在花钱和直接打里面取小的 打不过就只能花钱 这种方法就导致 如果怪兽的能力值很大 那么我们就需要很大的空间 所以引出下一种做法 纵…...
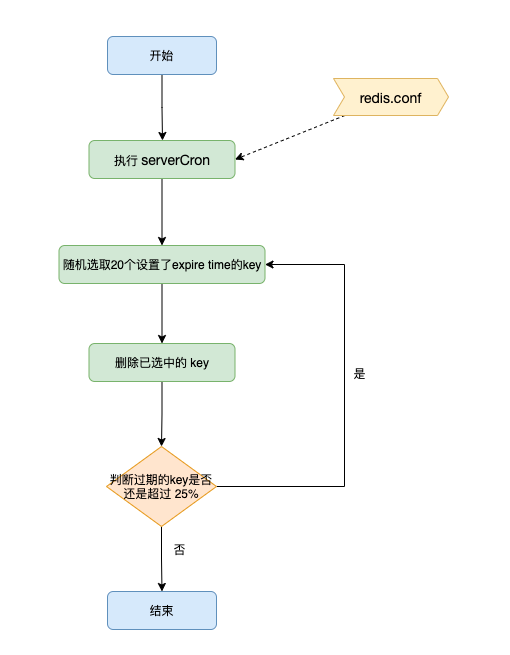
Redis过期数据的删除策略
1 介绍 Redis 是一个kv型数据库,我们所有的数据都是存放在内存中的,但是内存是有大小限制的,不可能无限制的增量。 想要把不需要的数据清理掉,一种办法是直接删除,这个咱们前面章节有详细说过;另外一种就是…...

如何使用CSS实现一个拖拽排序效果?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 实现拖拽排序效果的CSS和JavaScript示例⭐ HTML 结构⭐ CSS 样式 (styles.css)⭐ JavaScript 代码 (script.js)⭐ 实现说明⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦…...

leetcode 118.杨辉三角
⭐️ 题目描述 🌟 leetcode链接:https://leetcode.cn/problems/pascals-triangle/description/ 代码: class Solution { public:vector<vector<int>> generate(int numRows) {// 先开空间vector<vector<int>> v;v.…...

微服务框架之SpringBoot面试题汇总
微服务框架之SpringBoot面试题汇总 什么是Spring Boot? 多年来,随着新功能的增加,spring变得越来越复杂。Spring项目,我们必须添加构建路径或添加Maven依赖关系,配置应用程序服务器,添加spring配置。因此&…...

Promise详解
目录 一、前言:为什么会出现Promise?二、Promise是什么?2.1 Promise的初体验 三、使用Promise的好处?3.1 指定回调函数的方式更加灵活3.2 可以解决回调地狱问题,支持链式调用 四、Promise实例对象的两个属性五、resolve函数以及reject函数六、Promise…...

Oracle 查询(当天,月,年)的数据
Trunc 在oracle中,可利用 trunc函数 查询当天数据,该函数可用于截取时间或者数值,将该函数与 select 语句配合使用可查询时间段数据 查询当天数据 --sysdate是获取系统当前时间函数 --TRUNC函数用于截取时间或者数值,返回指定的…...
什么是梯度下降
什么是梯度下降 根据已有数据的分布来预测可能的新数据,这是回归 希望有一条线将数据分割成不同类别,这是分类 无论回归还是分类,我们的目的都是让搭建好的模型尽可能的模拟已有的数据 除了模型的结构,决定模型能否模拟成功的关键…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
