FOC之SVPWM学习笔记
一、参考资料
- 【自制FOC驱动器】深入浅出讲解FOC算法与SVPWM技术 - 知乎
- FOC入门教程_zheng是在下的博客-CSDN博客
- DengFOC官方文档
- 技术干货 |【自制】FOC驱动板
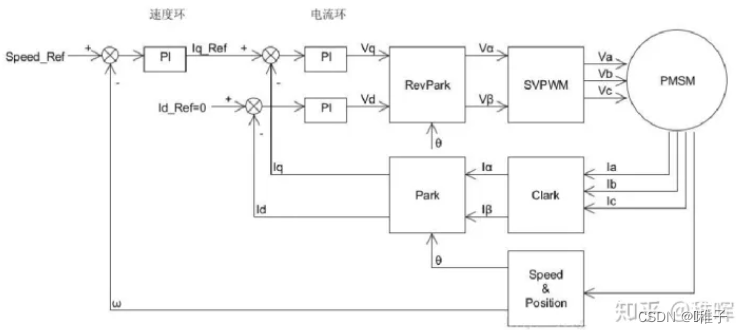
二、FOC控制算法流程框图
- 在FOC控制中主要用到三个PID环,从内到外依次是:电流环、速度环、位置环
- 通过电流反馈来控制电机电流(扭矩)→通过控制扭矩来控制电机的转速→通过控制电机的转速控制电机位置

2.1 PI电流环(内层)
 2.2 电流环+速度环
2.2 电流环+速度环
- w:电机的转速,可以通过电机编码器或者霍尔传感器计算得到
2.3 位置环+速度环+电流环
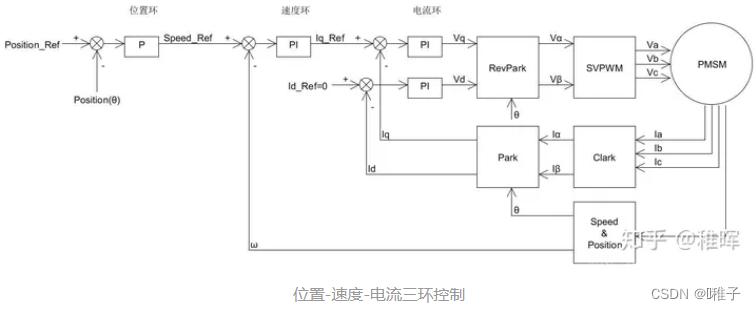
- 编码器无法返回电机的转速w,可以通过计算一定时间内的编码值变化量来表示电机的转速(用平均速度代表瞬时速度)。
- 电机转速比较高时,这样的方法是可以的。但是在位置控制模式时,电机的转速会很慢(因为需要转子固定在某个位置),此时用平均测速法会存在非常大的误差(转子不动或动的很慢,编码器就没有输出或者只输出1、2个脉冲)。
- 所以为了避免速度环节带来的误差,在做位置控制时,可以只使用位置和电流组成的双环进行控制。此时位置环使用PID控制(位置的微分D就是速度),可以减小位置控制的震荡,加快收敛,积分项的作用是为了消除静态误差。
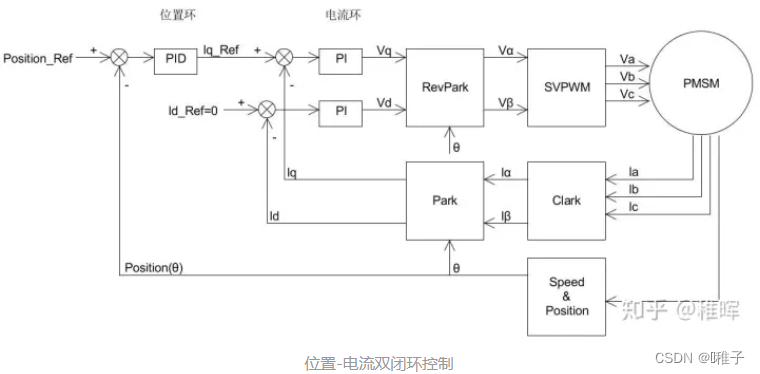
三、FOC控制算法重要公式
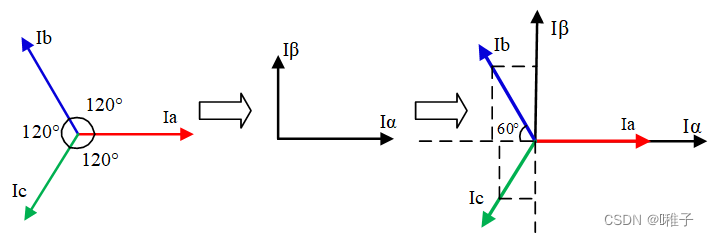
3.1 Clarke变换与反变换
- Clarke变换:将三相正弦电流Ia、Ib、Ic,转换成Iα、Iβ
- Clarke逆变换:用不到,采用了SVPWM进行了替代。
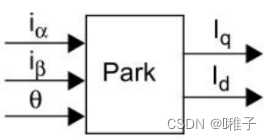
3.2 Park变换与反变换
- Park变换:将两相正弦电流Iα、Iβ,转换为两个常量Iq、Id
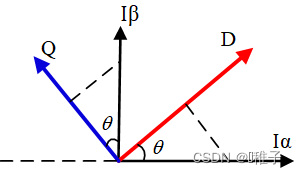
α--β坐标系:电机定子
q-d坐标系:电机转子
θ:转子当前的角度
Iq:当三相绕组产生的磁场方向与转子磁铁相切时,电流产生的旋转力矩最大。
Id:当三相绕组产生的磁场方向与转子磁场方向反向平行时,这时电机会被吸在原地不动,电流都用来产生热量。
- Iq=1,Id=0,转子逆时针旋转,且转速随着Iq的变大而变大。
- Iq=0,Id=1,转子定在原地,且发热量随着Id的变大而变大。
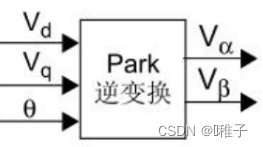
- Park逆变换:

3.3 扇区计算
在三相逆变电路中:
- 1:上桥臂导通
- 0:上桥臂关闭
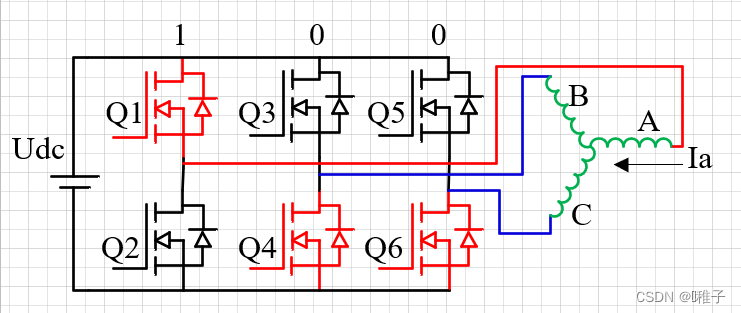
3.3.1 矢量编码
为了便于分析:采用二进制的方式对电压矢量进行编码,例如二进制100,十进制为U4
- 3个半桥臂共可产生8种输出状态(2^3=8)
- U7(111):3个半桥的上桥臂全部导通,无电流输出
- U0(000):3个半桥的上桥臂全部关闭,无电流输出
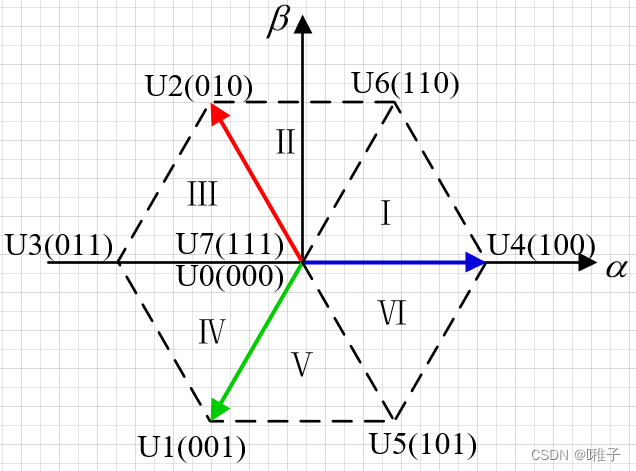
| 序号 | A相桥臂 | B相桥臂 | C相桥臂 | 矢量编号 |
| 1 | 0 | 0 | 0 | U0 |
| 2 | 1 | 0 | 0 | U4 |
| 3 | 1 | 1 | 0 | U6 |
| 4 | 1 | 1 | 1 | U7 |
| 5 | 0 | 1 | 1 | U3 |
| 6 | 0 | 0 | 1 | U1 |
| 7 | 0 | 1 | 0 | U2 |
| 8 | 1 | 0 | 1 | U5 |
3.3.2 七段式SVPWM调制
- 在合理的位置插入两个零矢量,并且在时间上进行平均分配,以使产生的PWM对称,从而有效地降低PWM的谐波分量。

| Uref所在的位置 | MOS开关切换顺序二进制编码 | 电压矢量切换顺序 |
| Ⅰ区(0<θ<60) | 000-100-110-111-111-110-100-000 | 0-4-6-7-7-6-4-0 |
| Ⅱ区(60<θ<120) | 000-010-110-111-111-110-010-000 | 0-2-6-7-7-6-2-0 |
| Ⅲ区(120<θ<180) | 000-010-011-111-111-011-010-000 | 0-2-3-7-7-3-2-0 |
| Ⅳ区(180<θ<240) | 000-001-011-111-111-011-001-000 | 0-1-3-7-7-3-1-0 |
| Ⅴ区(240<θ<300) | 000-001-101-111-111-101-001-000 | 0-1-5-7-7-5-1-0 |
| Ⅵ区(300<θ<360) | 000-100-101-111-111-101-100-000 | 0-4-5-7-7-5-4-0 |
3.3.3 扇区判断
相关文章:

FOC之SVPWM学习笔记
一、参考资料 【自制FOC驱动器】深入浅出讲解FOC算法与SVPWM技术 - 知乎FOC入门教程_zheng是在下的博客-CSDN博客DengFOC官方文档技术干货 |【自制】FOC驱动板 二、FOC控制算法流程框图 在FOC控制中主要用到三个PID环,从内到外依次是:电流环、速度环、位…...

DSO 系列文章(3)——DSO后端正规方程构造与Schur消元
文章目录 DSO代码注释:https://github.com/Cc19245/DSO-CC_Comments...

php 使用ES
Download Elasticsearch | Elastic <?phprequire vendor/autoload.php;use Elasticsearch\ClientBuilder;$client ClientBuilder::create()->build();# 索引一个文档 # Version 7.11 $params [index > my_index,id > my_id,body > [testField > abc] ];$…...
)
距离我成为炎帝的一次(比较近的一次)
sj登录—专业IT笔试面试备考平台_牛客网 这是dfs的一道基础题,可惜我还是没有学会 但是有时候错误也是一种成长方式 我的代码E题带路 #include<bits/stdc.h> //#define int long long using namespace std;const long long MAX1e310; //lon…...

Protobuf在IDEA中的插件安装教程
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
)
中间件(上)
1、何为中间件: 中间件(Middleware)是指位于操作系统和应用程序之间的一层软件层,用于提供各种服务和功能,以帮助不同的应用程序、系统或组件进行通信、交互和协作。中间件可以看作是在不同计算机或系统之间建立连接和…...

Python快速检验数据分布
假设检验的前提是确定数据的分布,本文介绍Python检验数据样本是否服从一定分布。使用方法是柯尔莫可洛夫-斯米洛夫检验(Kolmogorov–Smirnov test,K-S test),K-S检验方法适用于探索连续型随机变量的分布,对…...
uniapp微信小程序点击右上角菜单分享功能权限配置
个人项目地址: SubTopH前端开发个人站 (自己开发的前端功能和UI组件,一些有趣的小功能,感兴趣的伙伴可以访问,欢迎提出更好的想法,私信沟通,网站属于静态页面) SubTopH前端开发个人站…...

【OpenVINOSharp】在英特尔® 开发者套件爱克斯开发板使用OpenVinoSharp部署Yolov8模型
在英特尔 开发者套件爱克斯开发板使用OpenVinoSharp部署Yolov8模型 一、英特尔开发套件 AIxBoard 介绍1. 产品定位2. 产品参数3. AI推理单元 二、配置 .NET 环境1. 添加 Microsoft 包存储库2. 安装 SDK3. 测试安装4. 测试控制台项目 三、安装 OpenVINO Runtime1. 下载 OpenVINO…...

Django的模型层
Django的模型层1.Model的开发流程2.定义Model模型3.Model模型的实例4.Model模型的实战操作笔记开发流程1.在models.py中定义模型类,要求继承自models.Model2.生成迁移文件3.执行迁移5.定义属性1.字段类型2.字段选项3.关系模型实例1.类的属性2.创建对象3.实例的属性模…...
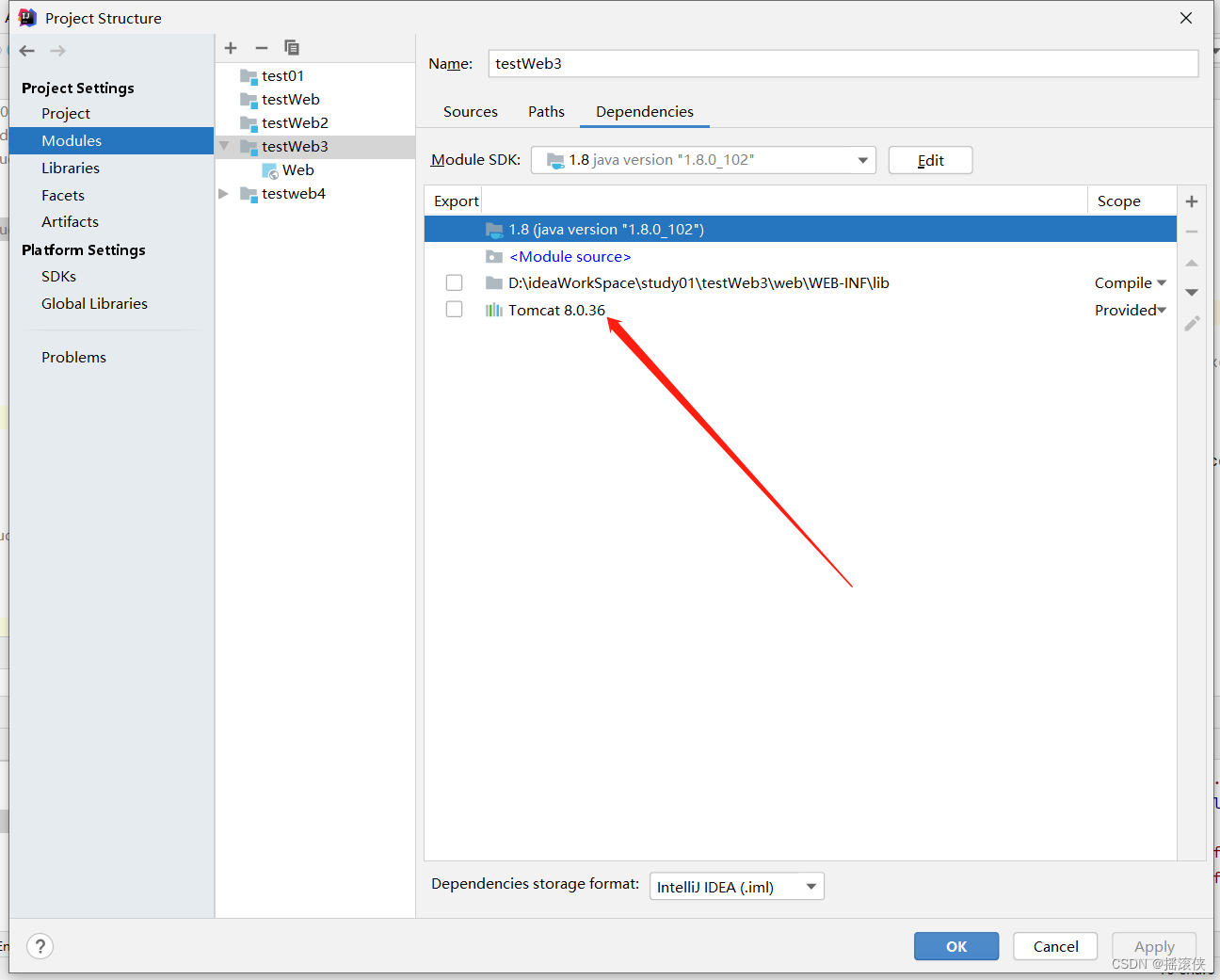
idea 新建servlet 访问提示404 WebServlet注解找不到包 报错
检查访问路径是否设置正确 如果设置为name “/testServlet”,则会404 WebServlet注解报错找不到包 检查是否引入了tomcat依赖包...

【EA-ISET协会】Elsevier|2区智慧农业类SCIEI, 进展顺,3个月左右录用~
一、期刊简介 2区智慧农业类SCI&EI 【期刊简介】IF: 3.0-4.0, JCR2区, 中科院4区; 【检索情况】SCI&EI双检,正刊; 【终审周期】走期刊部系统,3个月左右录用; 二、征稿范围 大数据和遥感技术在智慧农业中…...

Class类getName获取类名方法详细说明
1.说明 在java.lang.Class类中有一个获取类名的方法: public String getName() 其返回的是该对象表示的类或接口的名称。 返回由这个Class对象表示的实体的字符串名称, 这个实体可以是: class, interface, array class, primitive type, vo…...

凉而不冷 柔而不弱 三菱重工海尔舒适风科技助您整夜安眠
古人云:安寝乃人生乐事。可随着夏天的到来,昼长夜短,家里的老人、儿童、父母都存在不同的入睡苦恼。对于儿童来说,空调温度调的太低容易踢被子着凉,温度调的高又怕孩子满头大汗;父母自身也会因为半夜帮孩子…...

YOLOv5基础知识入门(7)— NMS(非极大值抑制)原理解析
前言:Hello大家好,我是小哥谈。NMS是指非极大值抑制(non maximum suppression),它是一种常用于物体检测任务的算法。在物体检测中,通常会有多个预测框(bounding box)被提议出来&…...

Gpt微信小程序搭建的前后端流程 - 后端基础框架的搭建(三)
Gpt微信小程序搭建的前后端流程 - 后端基础框架的搭建(三) Gpt微信小程序 只需要几个API,API上一小节也有讲到。直接用 gin 或者 beego 简单搭web服务器就够了。我们这里还用 go-micro微服务 去搭建,主要也是为了学以致用,把之前go-micro系列…...

jstat(JVM Statistics Monitoring Tool):虚拟机统计信息监视工具
jstat(JVM Statistics Monitoring Tool):虚拟机统计信息监视工具 用于监视虚拟机各种运行状态信息的命令行工具。 它可以显示本地或者远程虚拟机进程中的类加载、内存、垃圾收集、即时编译等运行时数据,在没有GUI图形界面、只提…...
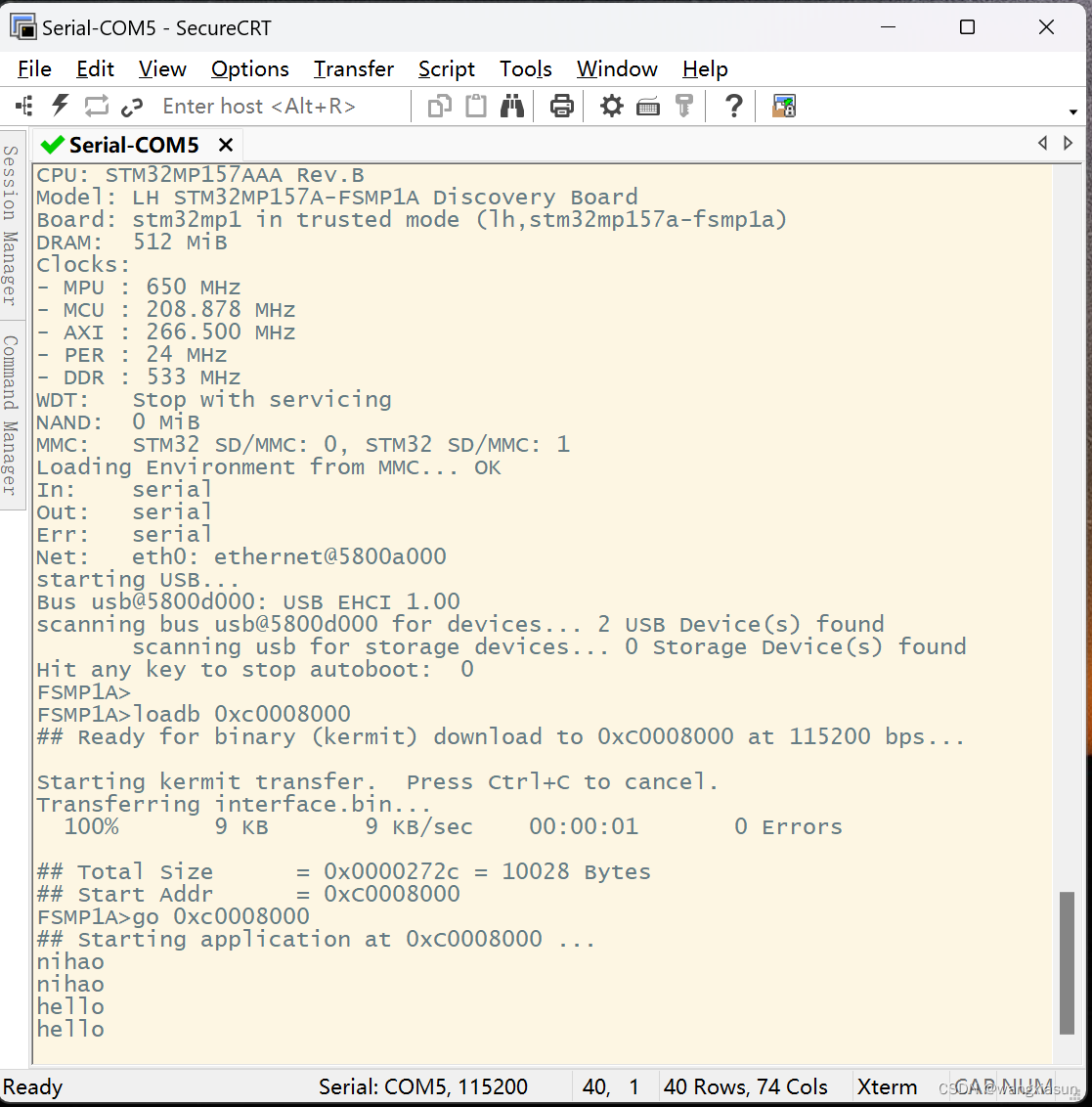
【ARM】Day6 cotex-A7核UART总线实验
cotex-A7核UART总线实验 1. 键盘输入一个字符‘a’,串口工具显示‘b’ 2. 键盘输入一个字符串"nihao",串口工具显示“nihao” uart.h #ifndef __UART4_H__ #define __UART4_H__#include "stm32mp1xx_rcc.h" #include "stm3…...

HTTPS代理搭建技巧分享
今天我们来分享一下如何搭建一个能够实现中间人 检测和防护的HTTPS代理。保护我们的网络通信安全是至关重要的,让我们一起学习如何构建一个安全可靠的HTTPS代理吧! 什么是中间人 ? 首先,让我们来了解一下什么是中间人 。中间人 是…...
第四章:树形结构的关联式容器(map+set)
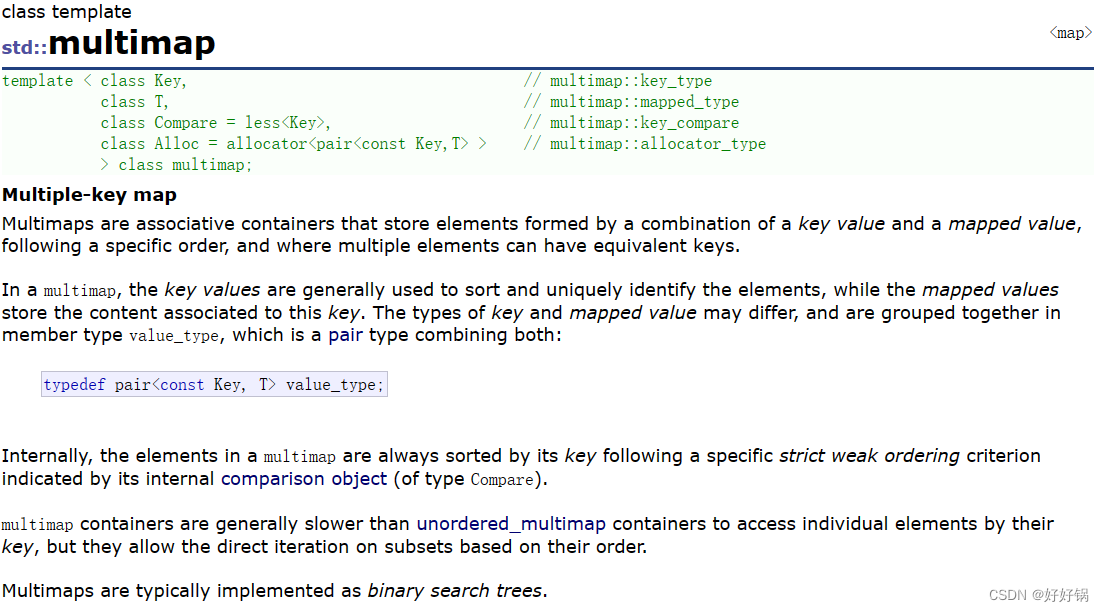
系列文章目录 文章目录 系列文章目录前言1、关联式容器与序列式容器1.1 键值对 2、set的介绍3、multiset的介绍3.1 接口count与容器multiset 4、map的介绍4.1 接口insert4.2 operator[]和at 5、multimap的介绍 前言 根据应用场景的不桶,STL总共实现了两种不同结构的…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...