USACO22OPEN Pair Programming G
P8273 [USACO22OPEN] Pair Programming G
题目大意
一个程序由一系列指令组成,每条指令的类型如下:
- × d \times d ×d,其中 d d d是一个 [ 0 , 9 ] [0,9] [0,9]范围内的整数
- + s +s +s,其中 s s s是一个表示变量名称的字符串,不同操作的变量名称互不相同
指令字符串中一个数字 d d d表示操作一,一个加号 + + +表示操作二。
小 B B B和小 E E E各有一个有 n n n条指令的程序,交错这些程序可以得到一个有 2 n 2n 2n个指令的新程序。计算执行这些交错程序可能得到的不同表达式的数量,输出答案对 1 0 9 + 7 10^9+7 109+7取模后的值。
有 T T T组数据。
1 ≤ T ≤ 10 , ∑ n ≤ 2000 1\leq T\leq 10,\sum n\leq 2000 1≤T≤10,∑n≤2000
题解
首先,要对小 B B B和小 E E E的字符串做一些处理。如果有 × 0 \times 0 ×0的操作,则之前的部分都没用了,但注意这个 × 0 \times 0 ×0还有用。如果有 × 1 \times 1 ×1操作,则对答案没有影响,要将其舍去。
设 f i , j , 0 / 1 f_{i,j,0/1} fi,j,0/1表示小 B B B的串匹配到第 i i i位,小 E E E的串匹配到第 j j j位,最后一个是小 B B B的指令还是小 E E E的指令的答案。
我们知道,加法和乘法都满足交换律,即 a + b = b + a , a × b = b × a a+b=b+a,a\times b=b\times a a+b=b+a,a×b=b×a。也就是说,如果有两个类型相同且位置相邻的操作,则两个操作的先后顺序对最后得到的表达式没有影响。
那么,如果两个字符串当前的操作类型相同,则先执行小 B B B的操作。
由此可推得转移式
f i + 1 , j , 0 = f i , j , 0 + f i , j , 1 f_{i+1,j,0}=f_{i,j,0}+f_{i,j,1} fi+1,j,0=fi,j,0+fi,j,1
f i , j + 1 , 1 = f i , j , 0 × [ S i ≠ T j + 1 ] + f i , j , 1 f_{i,j+1,1}=f_{i,j,0}\times [S_i\neq T_{j+1}]+f_{i,j,1} fi,j+1,1=fi,j,0×[Si=Tj+1]+fi,j,1
当最后一个指令是小 B B B的指令时,如果下一个指令要是小 E E E的指令,则必须满足两个指令的类型不同。这样就能保证没有表达式会被重复计算。
注意一开始 f 0 , 0 , 1 = 1 f_{0,0,1}=1 f0,0,1=1,如果将 1 1 1赋值到 f 0 , 0 , 0 f_{0,0,0} f0,0,0则会在下一次转移中被计算两次,所以要将 1 1 1赋值到 f 0 , 0 , 1 f_{0,0,1} f0,0,1才能使开始的空字符串只被计算一次。
时间复杂度为 O ( ∑ n 2 ) O(\sum n^2) O(∑n2)。
code
#include<bits/stdc++.h>
using namespace std;
const long long mod=1e9+7;
int T,n,s1,t1;
long long f[2005][2005][2];
char s[2005],t[2005];
void dd(int &a1,char a[]){a1=0;for(int i=1;i<=n;i++){if(a[i]=='0') a1=0;else if(a[i]=='1') continue;if(a[i]!='+') a[i]='*';a[++a1]=a[i];}
}
int main()
{scanf("%d",&T);while(T--){scanf("%d",&n);scanf("%s%s",s+1,t+1);dd(s1,s);dd(t1,t);f[0][0][1]=1;for(int i=0;i<=s1;i++){for(int j=0;j<=t1;j++){if(i<s1) f[i+1][j][0]=(f[i][j][0]+f[i][j][1])%mod;if(j<t1){f[i][j+1][1]=f[i][j][1];if(i&&s[i]!=t[j+1])f[i][j+1][1]=(f[i][j+1][1]+f[i][j][0])%mod;}}}printf("%lld\n",(f[s1][t1][0]+f[s1][t1][1])%mod);}return 0;
}
相关文章:

USACO22OPEN Pair Programming G
P8273 [USACO22OPEN] Pair Programming G 题目大意 一个程序由一系列指令组成,每条指令的类型如下: d \times d d,其中 d d d是一个 [ 0 , 9 ] [0,9] [0,9]范围内的整数 s s s,其中 s s s是一个表示变量名称的字符串ÿ…...

实战分享之springboot+easypoi快速业务集成
1.依赖引入 <!--引入EasyPOI--><dependency><groupId>cn.afterturn</groupId><artifactId>easypoi-base</artifactId><version>4.1.0</version></dependency><dependency><groupId>cn.afterturn</group…...
)
金字塔原理(思考的逻辑)
前言:前面学习了表达的逻辑,那在表达之前,如何组织内容?如何进行思考?接下来看第二篇——思考的逻辑。 目录 应用逻辑顺序 时间顺序 结构顺序 程度顺序 概括各组思想 什么是概括? 思想表达方式 如…...
和反向传播(Back propagation))
机器学习之前向传播(Forward Propagation)和反向传播(Back propagation)
前向传播(Forward Propagation)和反向传播(Back propagation)是深度学习中神经网络训练的两个关键步骤。 前向传播(Forward Propagation): 定义:前向传播是指从神经网络的输入层到输…...
Matlab高光谱遥感数据处理与混合像元分解实践技术
光谱和图像是人们观察世界的两种方式,高光谱遥感通过“图谱合一”的技术创新将两者结合起来,大大提高了人们对客观世界的认知能力,本来在宽波段遥感中不可探测的物质,在高光谱遥感中能被探测。以高光谱遥感为核心,构建…...

Docker consul的容器服务注册与发现
前言一、服务注册与发现二、consul 介绍三、consul 部署3.1 consul服务器3.1.1 建立 Consul 服务3.1.2 查看集群信息3.1.3 通过 http api 获取集群信息 3.2 registrator服务器3.2.1 安装 Gliderlabs/Registrator3.2.2 测试服务发现功能是否正常3.2.3 验证 http 和 nginx 服务是…...

Spring注入外部 工厂类Bean
问题 对于一些使用建造者模式的 Bean,我们往往不能直接 new 出来,这些 Bean 如果需要注册到 Spring 容器中,我们就需要使用工厂类。 比如我们项目中经常使用的okhttp: 如果我们想把OkHttpClient注册到Spring容器中,该怎么做? …...

WPF网格拖动自动布局效果
WPF网格拖动自动布局效果 使用Canvas和鼠标相关事件实现如下的效果: XAML代码: <Window x:Class="CanvasTest.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:...
排名)
肯德尔秩相关系数(Kendall‘s Tau)排名
肯德尔秩相关系数(Kendall’s Tau)是一种用于衡量两个排列之间相似性的统计指标,它考虑了元素之间的顺序关系而不考虑具体数值。该系数被广泛用于排序、排名和比较不同实验结果的相关性等领域。 具体而言,肯德尔秩相关系数衡量了…...

电脑怎么把视频转换gif动图?视频生成gif的操作步骤
如果你也想把一些精彩的视频转gif图片(https://www.gif.cn)的话,今天的文章你可千万不要错过,利用专业的视频转gif工具,轻松在线视频转gif,操作简单又方便,支持电脑、手机双端操作,赶…...
使用 docker 搭建 granfana+prometheus 监控平台监控测试服务器资源
互联网发展的今天,人们对互联网产品的用户体验要求也越来越高,企业为了能提供更优质的用户体验,就会绞尽脑汁想尽各种办法。而对于服务器的资源监控,搭建一个资源监控平台,就是一个很好的维护优质服务的保障平台。利用…...
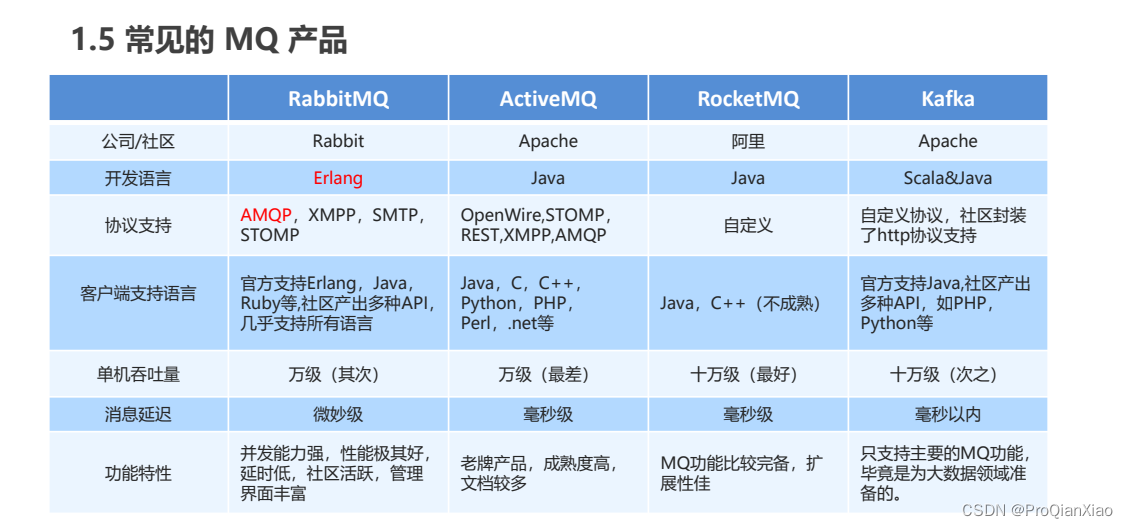
一、MQ的基本概念
1、初识MQ MQ全称是Message Queue,消息队列,多用于系统之间进行异步通信。队列的概念数据结构中有详细介绍过,先进先出,消息队列就是存储消息的数据结构。 同步调用和异步调用两者之间的区别: 同步调用:发…...

Android面试题:MVC、MVP、MVVM
MVC模式: MVC结构: 1.MVC(Model-View-Controller) 2.Model:对数据库的操作、对网络等的操作都应该在Model里面处理,当然对业务计算,变更等操作也是必须放在的该层的。 3.View:主要包括一下View及ViewGroup控件,可以是…...

vue js 回调函数 异步处理 为什么要 let that = this
1 异步就是开个事务(只有主线程 等主线程空闲),用that 值 做处理,然后返回处理结果,而that的值是开启事务那一刻的this的值.而在主线程处理的时候,this的一直在变化, that的值保留在那一刻 ps 或是将本obj 传递给其他的obj使用处理 ps 开启新事务或开启新子线程都是 在新的ob…...

前端面试:【算法与数据结构】常见数据结构解析
在计算机科学中,数据结构是组织和存储数据的方式。精通常见的数据结构对于解决计算机科学和编程问题至关重要。本文将深入探讨常见的数据结构:数组、链表、栈、队列和哈希表,以帮助你建立坚实的数据结构基础。 1. 数组(Array&…...
RTSP/Onvif视频服务器EasyNVR安防视频云服务平台出现崩溃并重启的情况解决方案
EasyNVR安防视频云服务平台的特点是基于RTSP/Onvif协议将前端设备统一接入,在平台进行转码、直播、处理及分发,在安防监控场景中,EasyNVR可实现实时监控、云端录像、云存储、告警、级联等视频能力,极大满足行业的视频监控需求。 有…...

软考高级系统架构设计师系列论文九十四:论计算机网络的安全性设计
软考高级系统架构设计师系列论文九十四:论计算机网络的安全性设计 一、计算机网络安全性设计相关知识点二、摘要三、正文四、总结一、计算机网络安全性设计相关知识点 软考高级系统架构设计师:计算机网络...
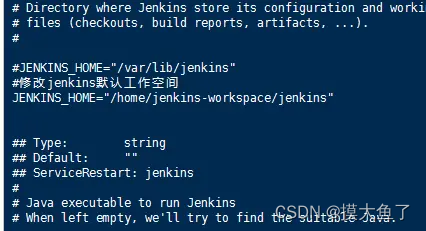
jenkins Linux如何修改jenkins 默认的工作空间workspace
由于jenkins默认存放数据的目录是/var/lib/jenkins,一般这个var目录的磁盘空间很小的,就几十G,所以需要修改jenkins的默认工作空间workspace 环境 jenkins使用yum安装的 centos 7 正题 1 查看jenkins安装路径 [rootlocalhost jenkins_old_data]# rpm…...

Mysql报错 mysqladmin flush-hosts
出现这个的原因是错误连接达到数据库设置的最大值。 此时需要释放重置连接最大值。 进入mysql使用命令 flush-hosts;环境说明: 内网测试服务器192.168.18.251 为WEB服务器,安装了mysql; 内网音视频转码服务器192.168.18.253安装了转码工具࿰…...
javaee idea创建maven项目,使用el和jstl
如果使用el表达式出现下图问题 解决办法 这是因为maven创建项目时,web.xml头部声明默认是2.3,这个默认jsp关闭el表达式 办法1 在每个需要用到el和jstl的页面的上面加一句: <% page isELIgnored"false" %> 方法2 修改web.xml文件开…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
