python连接Microsoft SQL Server 数据库
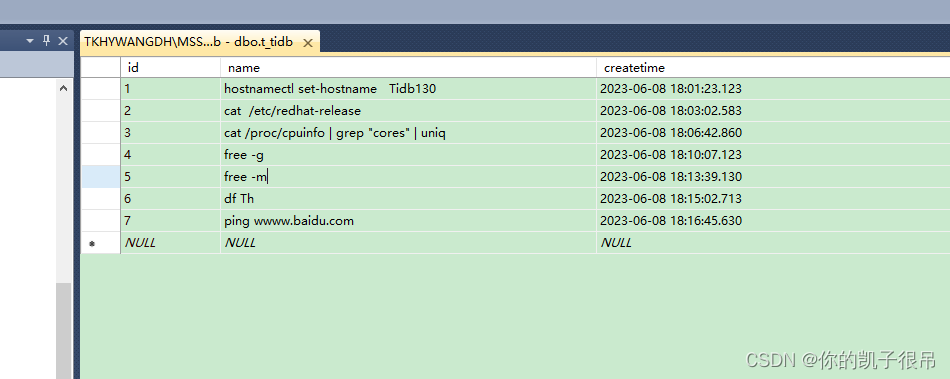
python代码
'''
Author: tkhywang 2810248865@qq.com
Date: 2023-08-21 11:22:24
LastEditors: tkhywang 2810248865@qq.com
LastEditTime: 2023-08-21 11:29:30
FilePath: \PythonProject02\Microsoft SQL Server 数据库.py
Description: 这是默认设置,请设置`customMade`, 打开koroFileHeader查看配置 进行设置: https://github.com/OBKoro1/koro1FileHeader/wiki/%E9%85%8D%E7%BD%AE
'''import pymssql as pymssql
# 连接数据库
conn = pymssql.connect('192.168.121.130', 'sa', 'Aa123456789', 'jiradb')
# 执行查询
cur = conn.cursor()
cur.execute("SELECT * FROM t_tidb")
# 获取结果
rows = cur.fetchall()
for row in rows:print(row)
# 关闭连接
cur.close()
conn.close()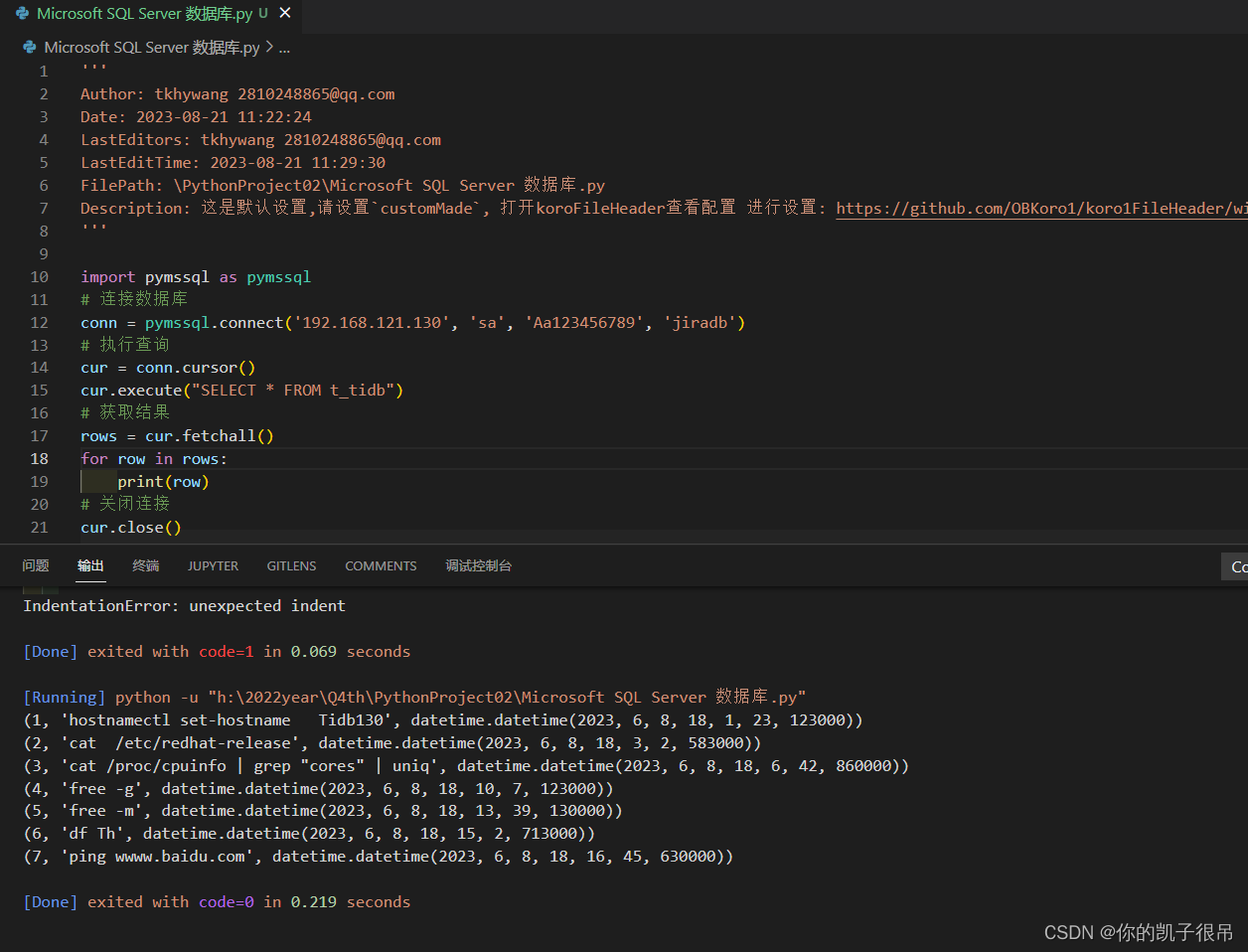
相关文章:

python连接Microsoft SQL Server 数据库
python代码 Author: tkhywang 2810248865qq.com Date: 2023-08-21 11:22:24 LastEditors: tkhywang 2810248865qq.com LastEditTime: 2023-08-21 11:29:30 FilePath: \PythonProject02\Microsoft SQL Server 数据库.py Description: 这是默认设置,请设置customMade, 打开koroFi…...
docker可视化工具
安装Portainer 官方安装说明:https://www.portainer.io/installation/ [rootubuntu1804 ~]#docker pull portainer/portainer[rootubuntu1804 ~]#docker volume create portainer_data portainer_data [rootubuntu1804 ~]#docker run -d -p 8000:8000 -p 9000:90…...
MySQL 用户管理操作
目录 一、用户管理概述 二、用户管理 1、创建用户 2、删除用户 三、账户密码管理 1、root用户修改自己的密码 2、ROOT用户修改其他普通用户密码 3、普通用户修改自己的密码 4、ROOT用户密码忘记解决办法 1)Linux系统 2)windows系统 四、用户权…...

【python办公自动化】PysimpleGUI中的popup弹窗中的按钮设置居中
PysimpleGUI中的popup弹窗中的按钮设置居中 背景问题解决背景 默认的popup弹窗中的OK按钮是在最下面偏左侧一些,有时需要将按钮放置居中 问题解决 首先找到pysimplegui源代码文件中popup的部分 然后定位到19388行,源文件内容如下 关于popup弹窗OK按钮的设置,将pad属性…...

postgresql 同步流复制两个相关参数synchronous_commit 和 synchronous_standby_names
一:synchronous_commit 1.synchronous_commit参数含义 这个参数用来设置事务提交返回客户端之前,一个事务是否需要等待 WAL 记录被写入磁盘。合法的值是{local,remote_write,remote_apply,on,off}。默认设置是on。 2.各可选值含义 2.1 local 当事务…...
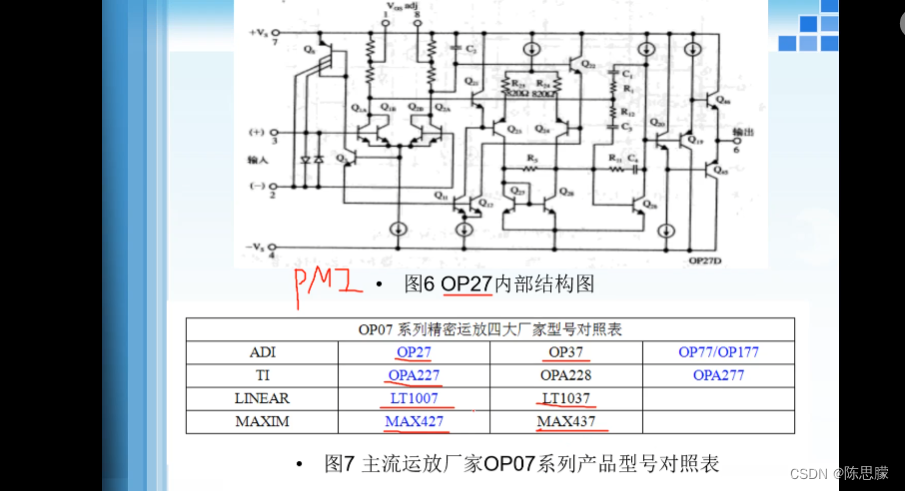
运算放大器发展史
在内部集成了一个补偿电容 MPS公司OP07推出后,大受欢迎。各家厂商都推出了自己的 这4款都是可以替换的...
LVS+Keepalived 实验
Keepalived 是什么 Keepalived 是一个基于VRRP协议来实现的LVS服务高可用方案,可以解决静态路由出现的单点故障问题的一款检查工具 在一个LVS服务集群中通常有主服务器(MASTER)和备份服务器(BACKUP)两种角色的服务器…...
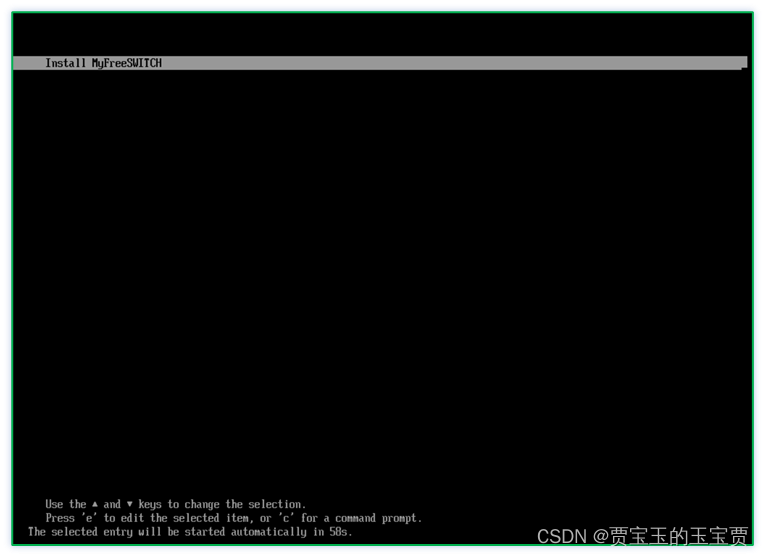
FreeSWITCH 1.10.10 简单图形化界面1 - docker/脚本/ISO镜像安装
FreeSWITCH 1.10.10 简单图形化界面1 - docker/脚本/ISO镜像安装 0. 界面预览1. Docker安装1.1 下载docker镜像1.2 启动docker镜像1.3 登录 2. 脚本安装2.1 下载2.2 安装2.3 登录2.4 卸载程序 3. 镜像安装3.1 下载镜像3.2 安装镜像3.3 登录 0. 界面预览 http://myfs.f3322.net…...
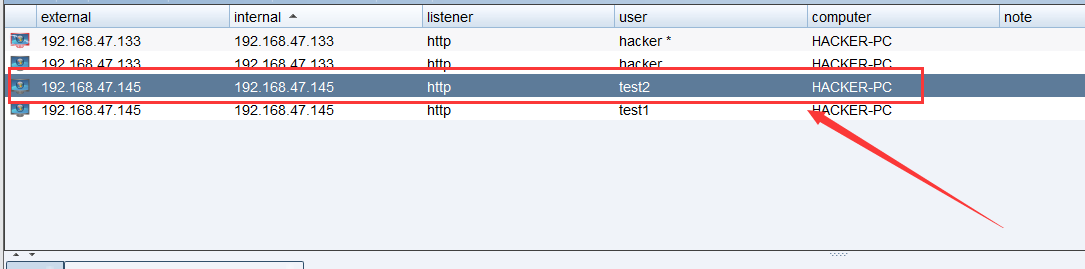
内网渗透神器CobaltStrike之权限提升(七)
Uac绕过 常见uac攻击模块 UAC-DLL UAC-DLL攻击模块允许攻击者从低权限的本地管理员账户获得更高的权限。这种攻击利用UAC的漏洞,将ArtifactKit生成的恶意DLL复制到需要特权的位置。 适用于Windows7和Windows8及更高版本的未修补版本 Uac-token-duplication 此攻…...
使用haproxy搭建web架构
haproxy HAProxy是一个免费的负载均衡软件,可以运行于大部分主流的Linux操作系统上。 HAProxy提供了可以在七层和四层两种负载均衡能力,它可以提供高可用性、负载均衡、及基于TCP和HTTP应用的代理。适用于负载大的Web站点,在运行在硬件上可…...
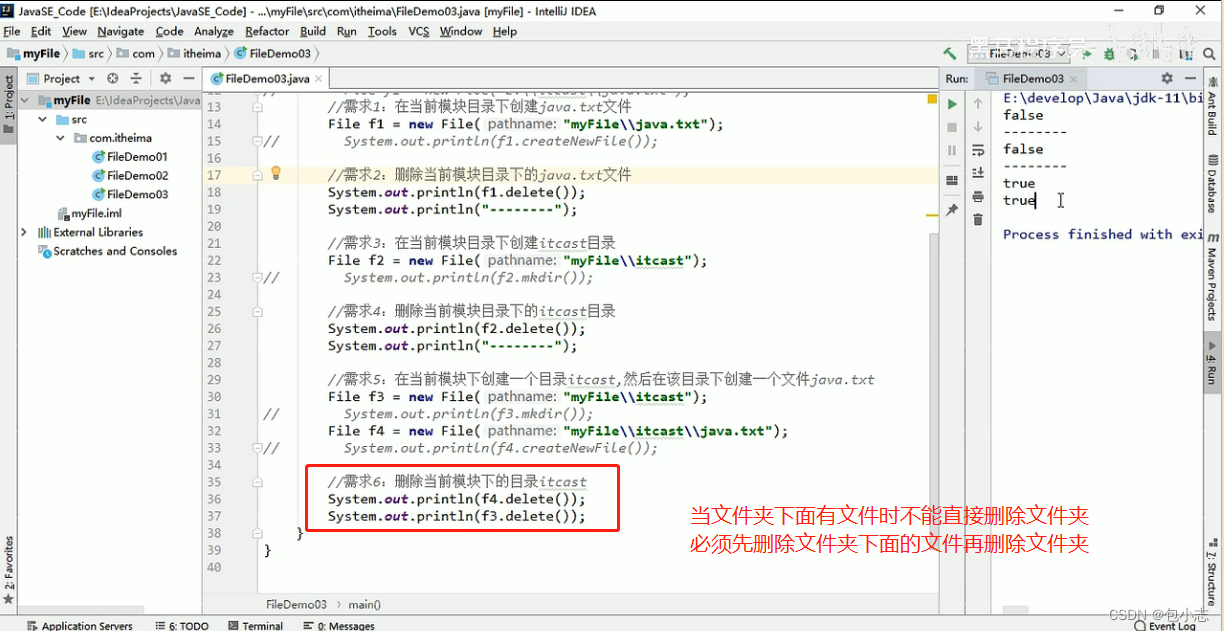
Java基础之IO流File类创建及删除
1.File类概述及构造方法 2.File类创建功能 文件创建成功! 如果文件不存在,就创建文件,并返回true 如果文件存在,就不创建文件,并返回false 如果文件夹不存在,就创建文件夹,并返回true 如果文件…...

高速道路监控:工业路由器助力高速监控远程管理与维护
工业路由器在物联网应用中扮演着重要的角色。物联网的发展使得大量设备和传感器能够互联互通,而工业路由器作为连接这些设备和网络的中间桥梁,承担着数据传输和安全管理的重要责任。 工业路由器能够为高速监控提供网络功能,实现户外无线网络部…...
【校招VIP】前端基础之post和get
考点介绍: get和post 是网络基础,也是每个前端同学绕不过去的小问题,但是在校招面试中很多同学在基础回答中不到位,或者倒在引申问题里,就丢分了。 『前端基础之post和get』相关题目及解析内容可点击文章末尾链接查看…...

如何合理设计API接口?
本规范仅适用于由服务器端发起调用请求、POST提交数据以及GET请求文本数据结果的API,统一采用UTF-8编码规则,采用JSON格式响应。 URL定义 API 服务接口应提供REST风格的HTTP(HTTPS) 接口: {protocol}://{domain}:{port}/{app}/{controller}/{action}?{query} 变量 含义 示…...

Jsp 解决out.print()输出多出空行
一、原因 在 JSP 中,HTML 标签和 JSP 指令之外的内容会被当作文本处理,包括空行、空格和制表符等。当 JSP 引擎解析 JSP 页面时,会将这些文本内容原封不动地输出到响应中。 http响应 二、解决方法 在Jsp页面最前端添加 <% page trimDir…...
SMC状态机 讲解2 从模型到SMC
SMC状态机 讲解2 从模型到SMC 1、实例化有限状态机(FSM)2、简单转换 Simple Transition3、外部环回转换 External Loopback Transition4、内部环回转换 Internal Loopback Transition5、转换动作6、转换Guard7、转换参数8、Entry 和 Exit动作9、Push 转换10、Pop转换…...

MyBatis-Plus的使用
MyBatis-Plus 1、mybatis-plus介绍 官网:https://baomidou.com/ MyBatis-Plus (简称 MP)是一个MyBatis的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效率而生。MyBatis-Plus提供了通用的mapper…...
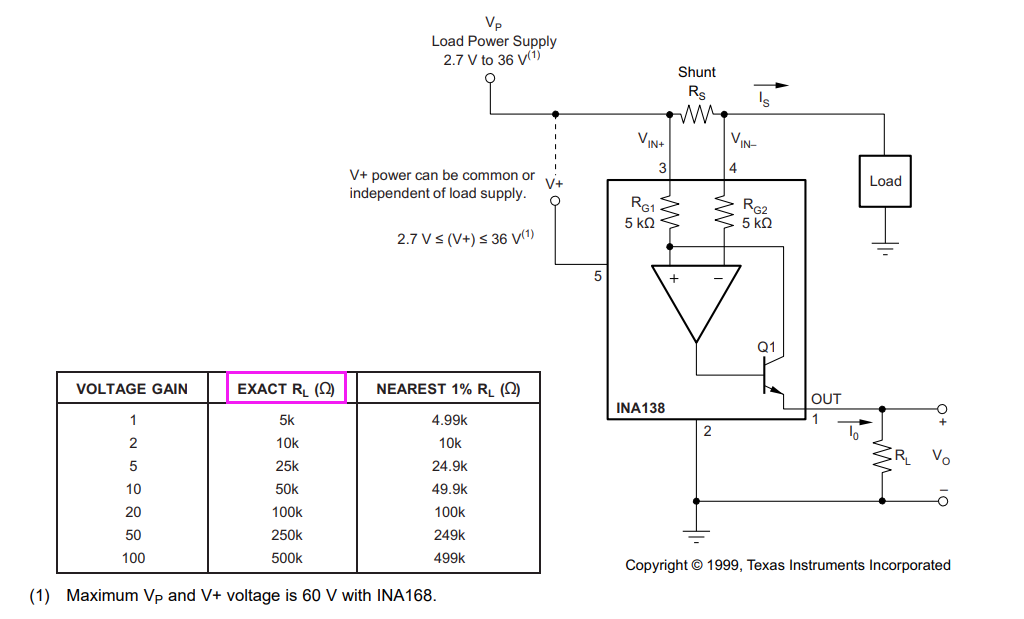
板卡设计+硬件每日学习十个知识点(44)23.8.24 (检测单元设计,接口部分设计,板卡电源输入设计,电源检测电路)
文章目录 1.检测单元介绍(使用GD32单片机)2.GD32的最小系统板3.GD32的温度监测4.GD32的电压监测和电流监测5.GD32的布线6.接口部分设计7.板卡电源输入设计8.电源检测电路 1.检测单元介绍(使用GD32单片机) 答: 首先要为…...
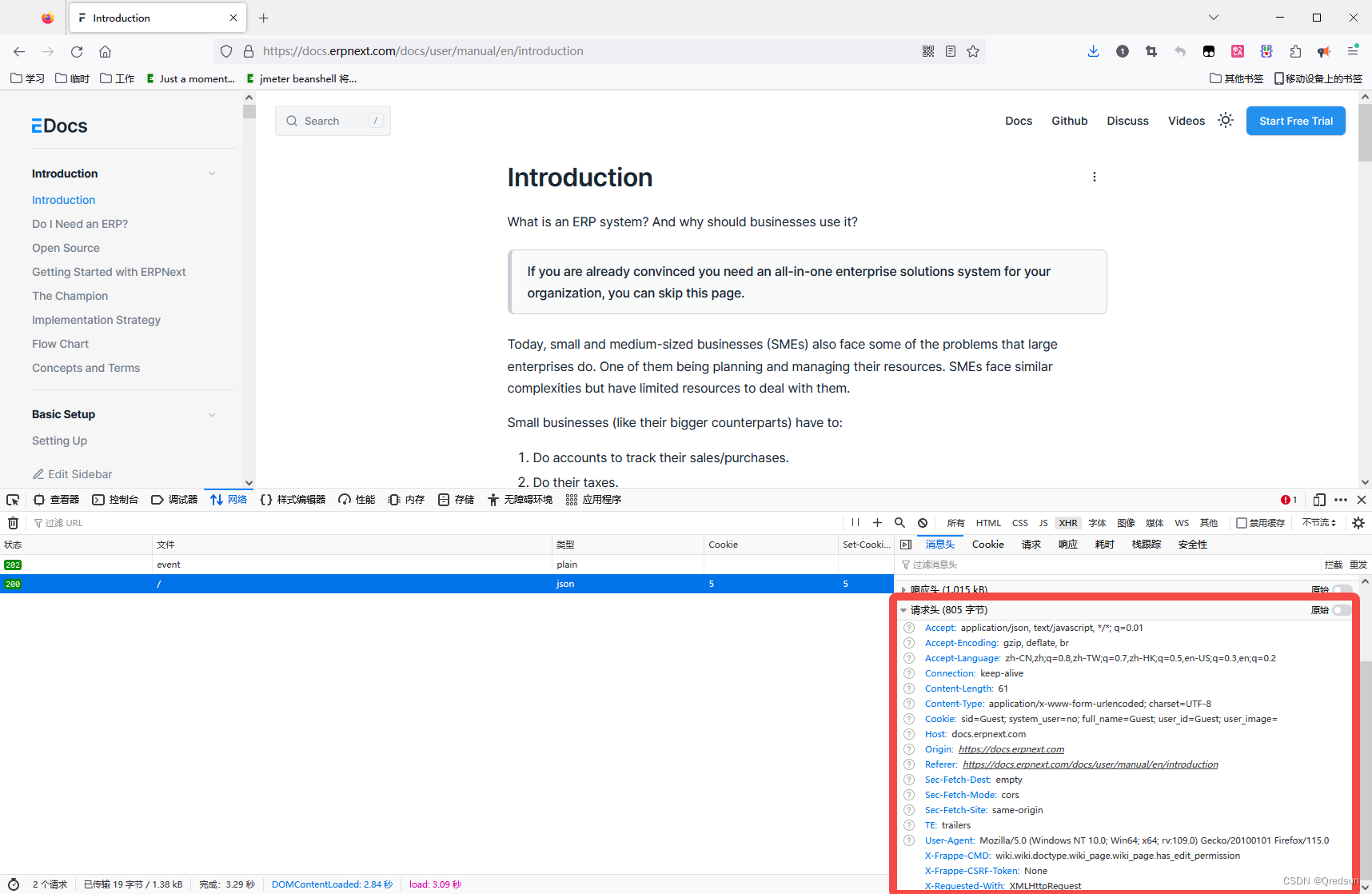
jmeter HTTP信息头管理器
首先,打开JMeter并创建一个新的测试计划。右键单击测试计划,选择"添加" > “线程组”,然后在线程组上右键单击,选择"添加" > “Sampler” > “HTTP请求”。 在HTTP请求中填写服务器的URL和其他必要…...

各种中间件的默认端口
面试时会忘记个别中间件端口 docker:2375 nacos:8848 redis:6379 rabbitMq: 5672(后台配置的端口)15672(web管理界面)账号:guest15674(web STOMP插件):通过WebSocket…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
