第十五天|104.二叉树的最大深度、111.二叉树的最小深度、 222.完全二叉树的节点个数
104.二叉树的最大深度
题目链接:104. 二叉树的最大深度 - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int GetDepth(TreeNode* Cur) {if (Cur == nullptr) return 0;int Left = GetDepth(Cur->left);int Right = GetDepth(Cur->right);return 1 + max(Left, Right);}int maxDepth(TreeNode* root) {return GetDepth(root);}
};111.二叉树的最小深度
题目链接:111. 二叉树的最小深度 - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int GetMin(TreeNode* Cur) {if (Cur == nullptr) return 0;int left = GetMin(Cur->left);int right = GetMin(Cur->right);if (Cur->left != nullptr && Cur->right == nullptr) return 1 + left;if (Cur->left == nullptr && Cur->right != nullptr) return 1 + right;return 1 + min(left, right);}int minDepth(TreeNode* root) {return GetMin(root);}
};222.完全二叉树的节点个数
题目链接:222. 完全二叉树的节点个数 - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int GetCount(TreeNode* Cur) {if (Cur == nullptr) return 0;int left = GetCount(Cur->left);int right = GetCount(Cur->right);return 1 + left + right;}int countNodes(TreeNode* root) {return GetCount(root);}
};相关文章:

第十五天|104.二叉树的最大深度、111.二叉树的最小深度、 222.完全二叉树的节点个数
104.二叉树的最大深度 题目链接:104. 二叉树的最大深度 - 力扣(LeetCode) /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullp…...

图像识别技术在医疗领域的革命:探索医学影像诊断的未来
导言: 随着人工智能和计算机视觉的快速发展,图像识别技术在医疗领域正掀起一场革命。医学影像诊断是医疗工作中的重要环节,而图像识别技术的引入为医生提供了更准确、高效的辅助手段。本文将深入探讨图像识别技术在医疗领域的应用,…...
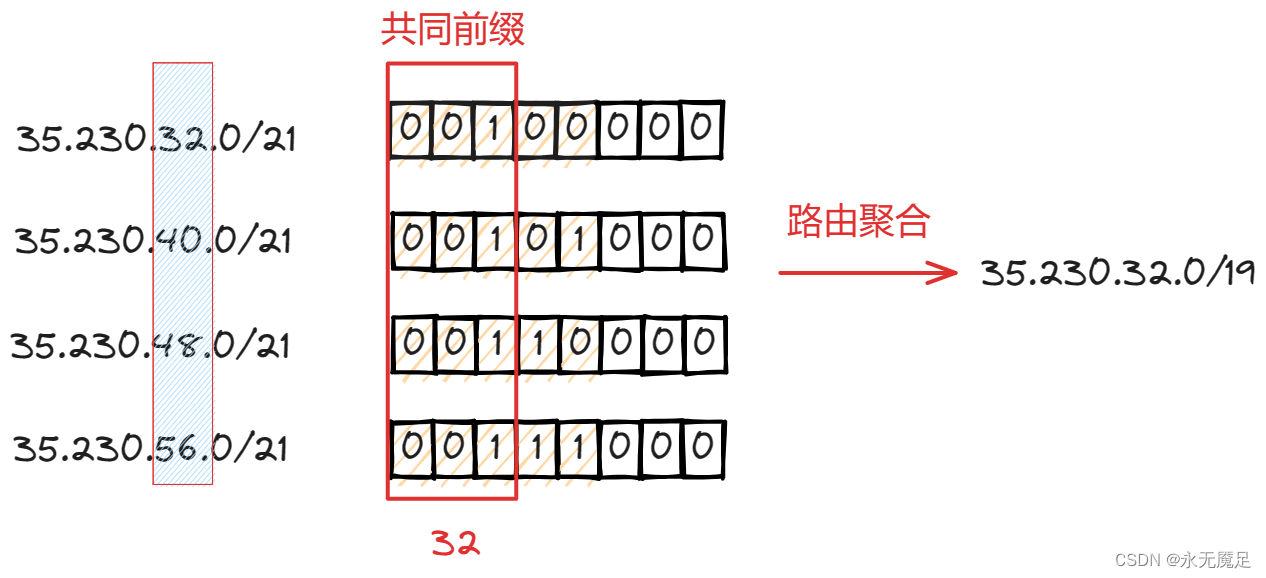
计网第四章(网络层)(二)
目录 IPV4地址编址 第一历史阶段(分类编址): A类地址: B类地址: C类地址: D类地址(多播地址): E类地址(保留地址): 第二历史阶…...

原生微信小程序使用 wxs;微信小程序使用 vant-weapp组件
1.原生微信小程序使用 wxs 1.内嵌 WXS 脚本 2. 定义外链 wxs 3. 使用外连wxs 在这里插入图片描述 2. 微信小程序使用 vant weapp 1.安装步骤 2. 安装包管理(package.json)文件的方法 操作顺序 :文档地址 如果使用 typescript 需要操作步骤3,否则不…...
qml相关知识1
qml相关知识1 QtQuick.Controls 哪个版本支持TreeModel 和 TreeItemqt5.12开始,TreeItem 类被删除,无法使用delegate 什么时候可以用Qt5.15中没有 import QtQuick.Controls 1吗,哪个版本有control1qml如何两种版本的controls混用(…...

linux+c+qt杂记
虚拟机网络选择; 桥接模式:设置window宿主机的IP/dns,把虚拟机设置为桥接即可。 切换到终端:我的是 ctrlaltFnF1? 问题解决: Ubuntu系统下载(清华大学开源软件镜像站)(ubuntu-20.…...

shouldComponentUpdate有什么作用?
触发时机 当props或state发生变化时,shouldComponentUpdate() 会在渲染执行之前被调用。 作用 根据shouldComponentUpdate()的返回值,判断react组件的输出是否受当前state或props更改影响。默认行为是state每次发生变化组件都会重新渲染。 shouldCompo…...

华为OD-滑动窗口最大值
题目描述 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例一 输入:nums [1,3,-1,-3,5,3,6,7], k 3 输出…...

Linux:ansible自动化运维工具
环境介绍 当前所有执行权限我是在root下执行的,如果提示权限之类的,可以在每句命令前 加上 sudo ansible主服务器 192.168.0.194 另外两个客户端分别为 192.168.0.193 192.168.0.192 软件只需要在主服务器上安装,客户端不需…...

前端如何使用WebSocket发送消息
系列文章目录 文章目录 系列文章目录前言一、WebSocket的基本原理二、在前端使用WebSocket1.创建WebSocket实例2.监听事件3.发送消息三、实际应用场景总结前言 WebSocket是一种在Web应用程序中实现双向通信的技术,它允许服务器和客户端之间实时交换数据。在本篇博客中,我们将…...

纸贵科技连续三年蝉联IDC中国 FinTech 50榜单
近日,国际权威市场研究机构IDC公布了“2023 IDC中国FinTech 50榜单”。作为领先的区块链技术和解决方案服务商,纸贵科技凭借过硬的区块链技术和丰富的金融科技创新成果,连续第三年荣登IDC中国FinTech 50榜单。 IDC中国FinTech 50榜单是金融科…...

台积电美国厂施工现场混乱,真令人头痛 | 百能云芯
近日,英伟达公司的财报表现异常亮眼,摩根士丹利不仅点名了台积电成为最大的受益者,还预测每售出一颗H100英伟达芯片,台积电就能获得900美元的利润。然而,美国媒体却曝出了一则不利的消息,称美国亚利桑那州的…...
React绑定antd输入框,点击清空或者确定按钮实现清空输入框内容
其实实现原理和vue的双向绑定是一样的,就是监听输入框的onChange事件,绑定value值,当输入框内容发生变化后,就重新设置这个value值。 示例代码:我这里是统一在handleCancel这个函数里面处理清空逻辑了,你们…...

Springboot整合liquIbase组件
liquIbase方式 1、添加依赖 <!-- Liquibase 依赖 --> <dependency><groupId>org.liquibase</groupId><artifactId>liquibase-core</artifactId> </dependency>2、添加配置项 spring:# datasource 数据源配置内容,对应…...
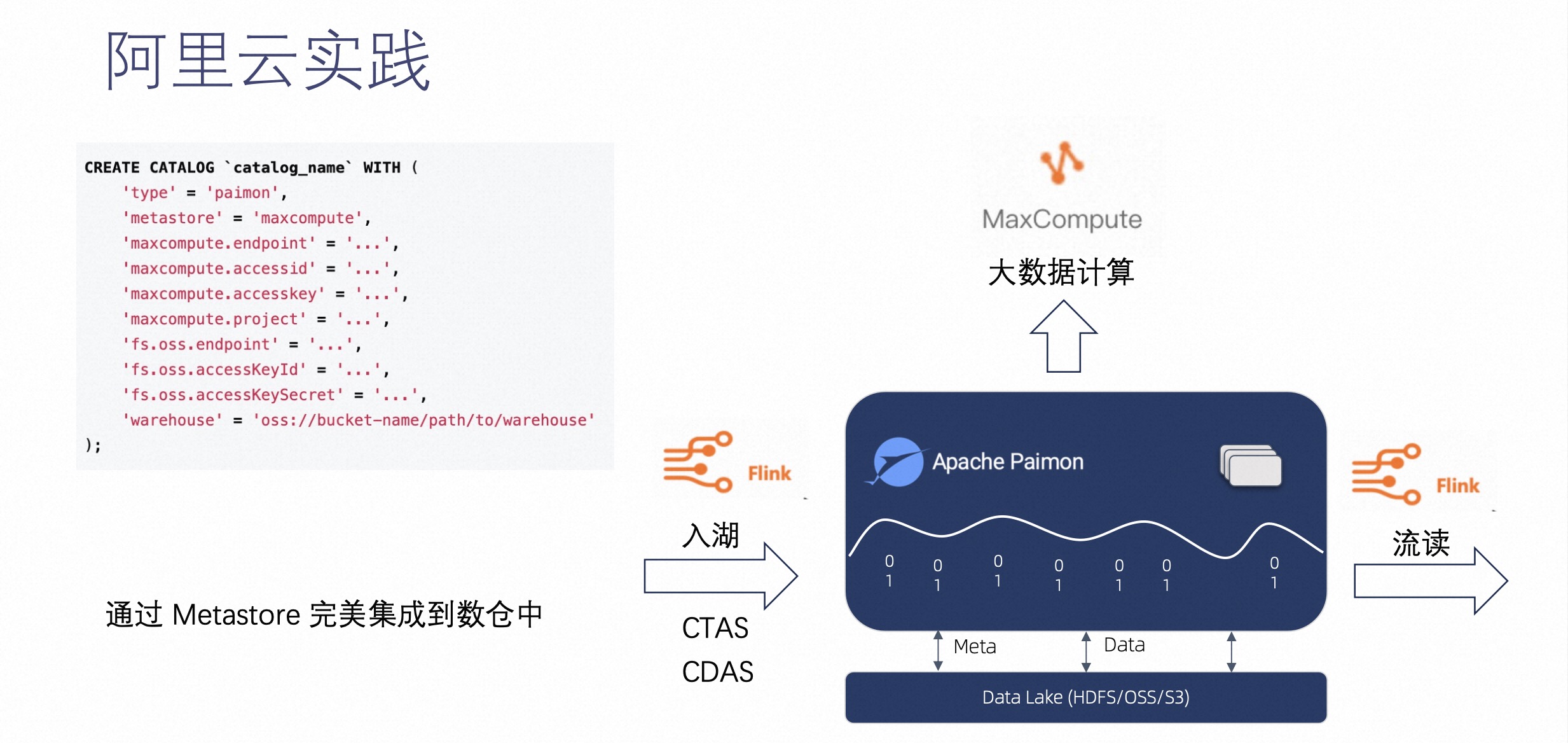
Apache Paimon 实时数据湖 Streaming Lakehouse 的存储底座
摘要:本文整理自阿里云开源大数据表存储团队负责人,阿里巴巴高级技术专家李劲松(之信),在 Streaming Lakehouse Meetup 的分享。内容主要分为四个部分: 流计算邂逅数据湖 Paimon CDC 实时入湖 Paimon 不止…...
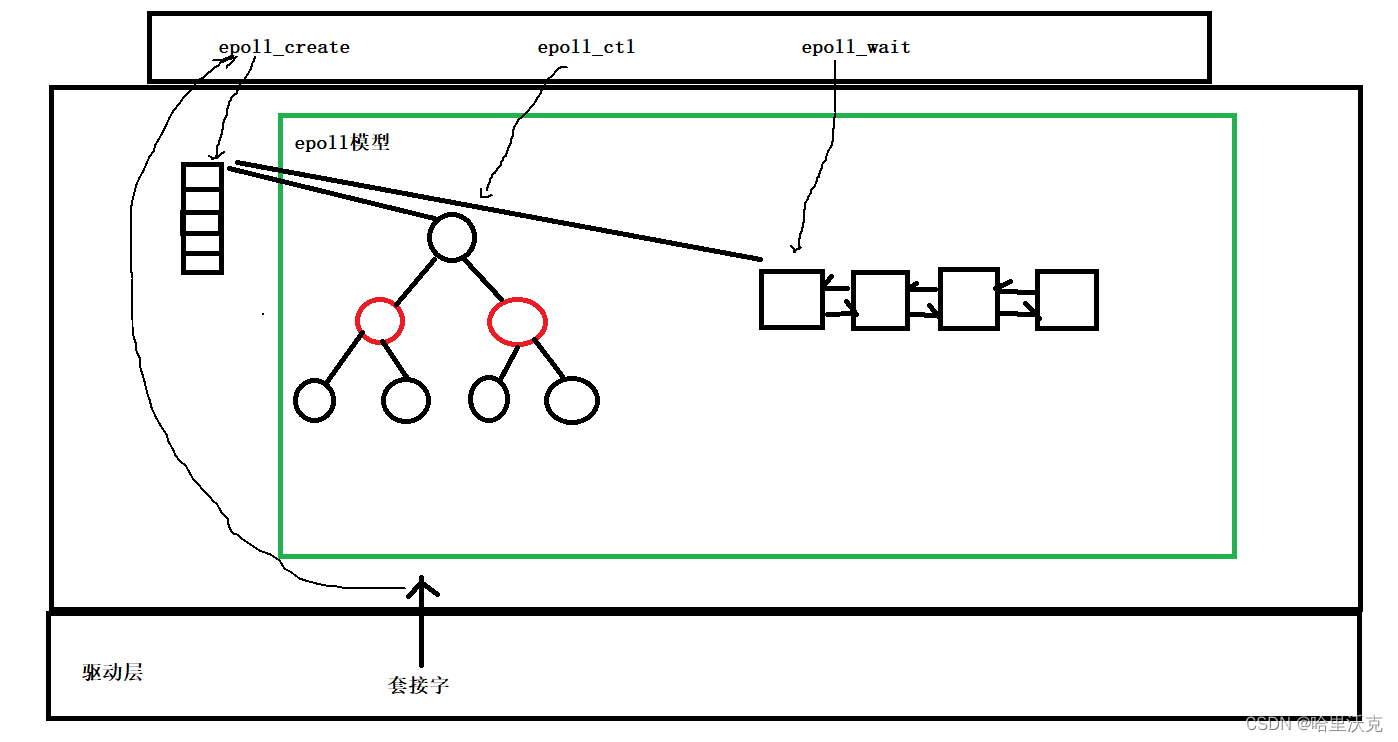
计算机网络(10) --- 高级IO
计算机网络(9) --- 数据链路层与MAC帧_哈里沃克的博客-CSDN博客数据链路层与MAC帧https://blog.csdn.net/m0_63488627/article/details/132178583?spm1001.2014.3001.5501 1.IO介绍 1.IO本质 1.如果数据没有出现,那么读取文件其实会被阻塞住…...

学习中ChatGPT的17种用法
ChatGPT本质上是一个聊天工具,旧金山的人工智能企业OpenAI于2022年11月正式推出ChatGPT。那么,ChatGPT与其他人工智能产品相比有什么特殊呢? 它除了可以回答结构性的问题,例如语法修正、翻译和查找答案之外。最关键的是它能够去解…...
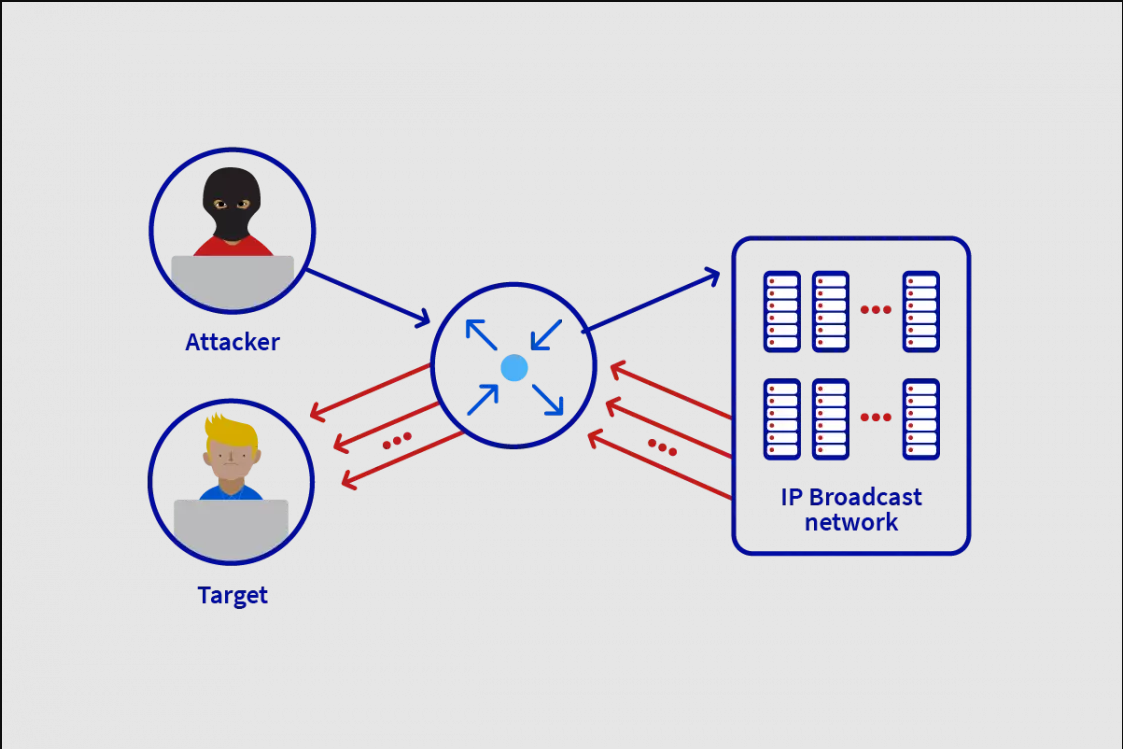
融合CDN 如何有效的抵抗DDoS攻击
绝大部分对外网站所有者都离不开CDN的支持,据统计,全球高达70%的互联网流量都是通过CDN来进行缓存和加速的,不论是国外知名的CDN厂商:如Cloudflare、AWS、Akamai等,还是国内主流的CDN厂商阿里云华为云腾讯云等…...
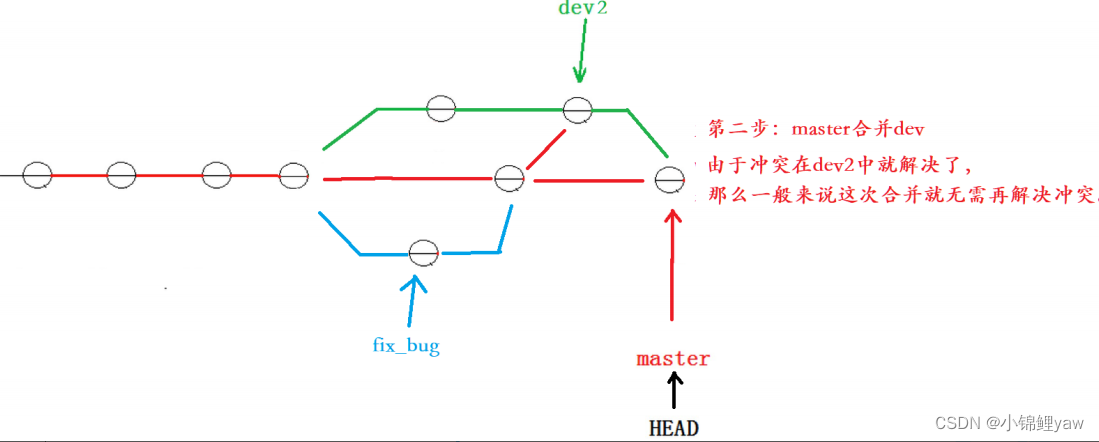
Git 原理与使用
1.版本控制器 所谓的版本控制器,就是能让你了解到⼀个⽂件的历史,以及它的发展过程的系统。通俗的讲就是⼀个可以记录⼯程的每⼀次改动和版本迭代的⼀个管理系统,同时也⽅便多⼈协同作业。 ⽬前最主流的版本控制器就是 Git 。Git 可以控制电脑…...

如何批量加密PDF文件并设置不同密码 - 批量PDF加密工具使用教程
如果你正在寻找一种方法来批量加密和保护你的PDF文件,批量PDF加密工具是一个不错的选择。 它是一个体积小巧但功能强大的Windows工具软件,能够批量给多个PDF文件加密和限制,包括设置打印限制、禁止文字复制,并增加独立的打开密码。…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...
