七大排序算法详解
1.概念
1.排序的稳定性
常见的稳定的排序有三种:直接插入排序,冒泡排序,归并排序
对于一组数据元素排列,使用某种排序算法对它进行排序,若相同数据之间的前后位置排序后和未排序之前是相同的,我们就成这种排序算法具有稳定性
单看单个属性的稳定性并无意义,稳定性主要体现在对具有多个属性的对象进行排序时才有意义
假设一个订单对象有两个属性,分别是下单时间与下单金额:
此时我们有一个需求,就是按照订单金额从高到低排序,若金额相同,则按照下单的先后时间排序
- 方法一:就是先按照订单金额大小排序,然后把金额相同的订单再次按照时间排序,但是这样就需要进行多次排序
- 方法二:如果我们先把订单按照下单时间的先后排好序,然后再按照订单金额排序,此时如果我们使用的排序是稳定性的,那么它排序后同样是按照下单顺序先后排列的,此时我们就只需要两次排序
所以排序的稳定性也是非常重要的
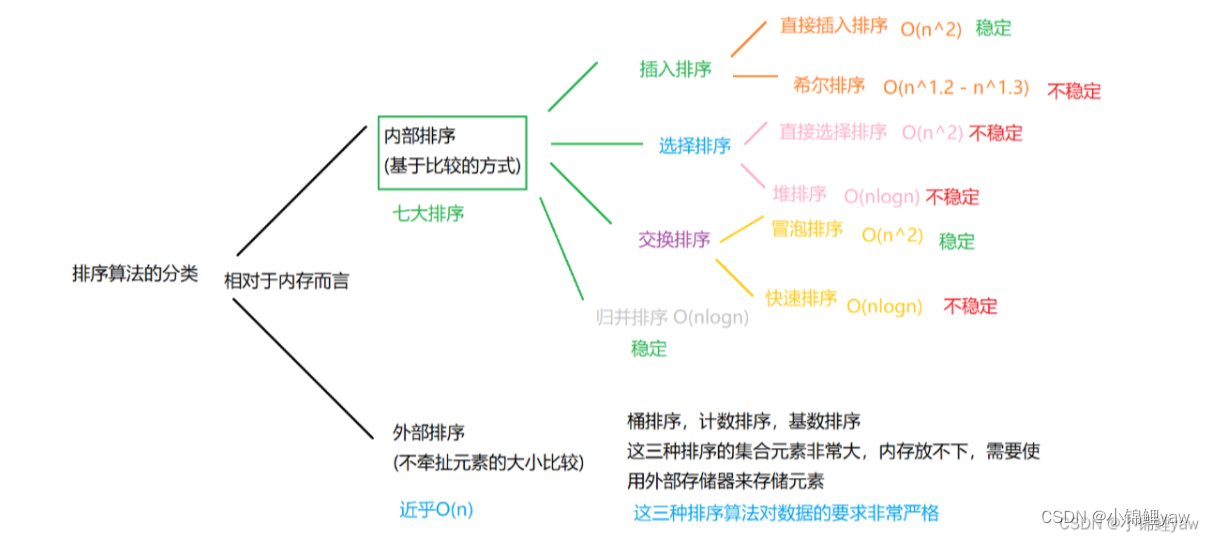
2.排序分类
1.外部排序(不牵扯元素大小比较)
外部排序主要有,桶排序,计数排序,基数排序,时间复杂度近乎O(n)
这三种排序的集合元素非常大,内存放不下,需要使用外部存储器来存储排序,并且对数据的要求非常严格
2.内部排序(基于比较的方式)
1.插入排序
⭐直接插入排序(稳定)
1.核心思路
每次从无序区间中选择第一个元素,插入到有序区间的合适位置(相当于打扑克牌码牌的过程),有序区间+1,无序区间-1,直至整个数组有序

⭐⭐⭐直接插入排序在近乎有序的集合性能上非常好(是因为近乎有序的集合,不需要频繁的去交换),常常作为其他高阶排序的优化手段
2.详细代码
/*** 直接插入排序* @param nums*/public static void insertSort(int[] nums) {// 有序区间[0,i)// 无序区间[i,n)for (int i = 1; i < nums.length; i++) {for (int j = i; j-1 >= 0; j--) {// 若当前值比前一个位置值还小,交换位置if (nums[j] < nums[j-1]) {swap(nums, j , j-1);}}}}
⭐希尔排序
希尔排序是对插入排序的优化,因为插入排序在近乎有序的数组上性能很好,希尔排序正是利用了这一点
1.核心思路
希尔排序不断地将原数组分为若干个子数组,先将子数组内部调整为有序,不断变大分组的长度,当分组长度为1时(一个元素天然有序),此时进行一次插入排序即可

2.详细代码
// 希尔排序public static void shellSort(int[] arr) {int gap = arr.length >> 1;while (gap > 1) {// 先按照gap分组,组内使用插入排序insertionSortByGap(arr,gap);gap = gap >> 1;}// 当gap == 1时,整个数组接近于有序,此时来一个插入排序insertionSortByGap(arr,1);}// 按照gap分组,组内的插入排序private static void insertionSortByGap(int[] arr, int gap) {// i初始化为0也可以,更容易理解for (int i = gap; i < arr.length; i++) {for (int j = i; j - gap >= 0 && arr[j] < arr[j - gap] ; j -= gap) {swap(arr,j,j - gap);}}}
2.选择排序
⭐直接选择排序(不稳定)
1.核心思路
每次在无序区间选择最小值与无序区间第一个位置元素交换,有序区间+1,无序区间-1,直至整个数组有序

2.详细代码
/*** 直接选择排序* @param nums*/public static void selectionSort(int[] nums) {// 起始状态:有序区间[0,i)// 无需区间[i,n)for (int i = 0; i < nums.length - 1; i++) {// 指向当前无需区间最小值的下标int minIndex = i;for (int j = i+1; j < nums.length; j++) {// 若当前值比最小值还小if (nums[j] < nums[minIndex]) {// 更新最小值下标minIndex = j;}}// 此时minIndex指向无需区间的最小值,将其加载有序区间的后面,有序区间+1,无序区间-1swap(nums, i, minIndex);}}
⭐堆排序
堆排详情博客:
原地堆排序
3.交换排序
⭐冒泡排序(稳定)
1.核心思路
每次遍历将无序数组的最大元素交换至末尾,无序数组-1,有序数组+1,直至整个数组有序
2.详细代码
// 无序区间[0...i]// 有序区间[]public static void bubbleSort(int[] arr) {// 外层循环表示要进行元素操作的趟数for (int i = 0; i < arr.length - 1; i++) {boolean isSwaped = false;for (int j = 0; j < arr.length - i - 1; j++) {if (arr[j] > arr[j + 1]) {isSwaped = true;swap(arr,j,j + 1);}}if (!isSwaped) {break;}}}
⭐快速排序(不稳定)
1.核心思路
每次从无序数组中选取一个元素作为分区点(pivot),将原集合中所有<pivot的元素都放在分区点的左侧,将所有>pivot的元素都放在分区点的右侧,这样分区点最终位置就确定了,继续在左半区间和右半区间重复此过程即可
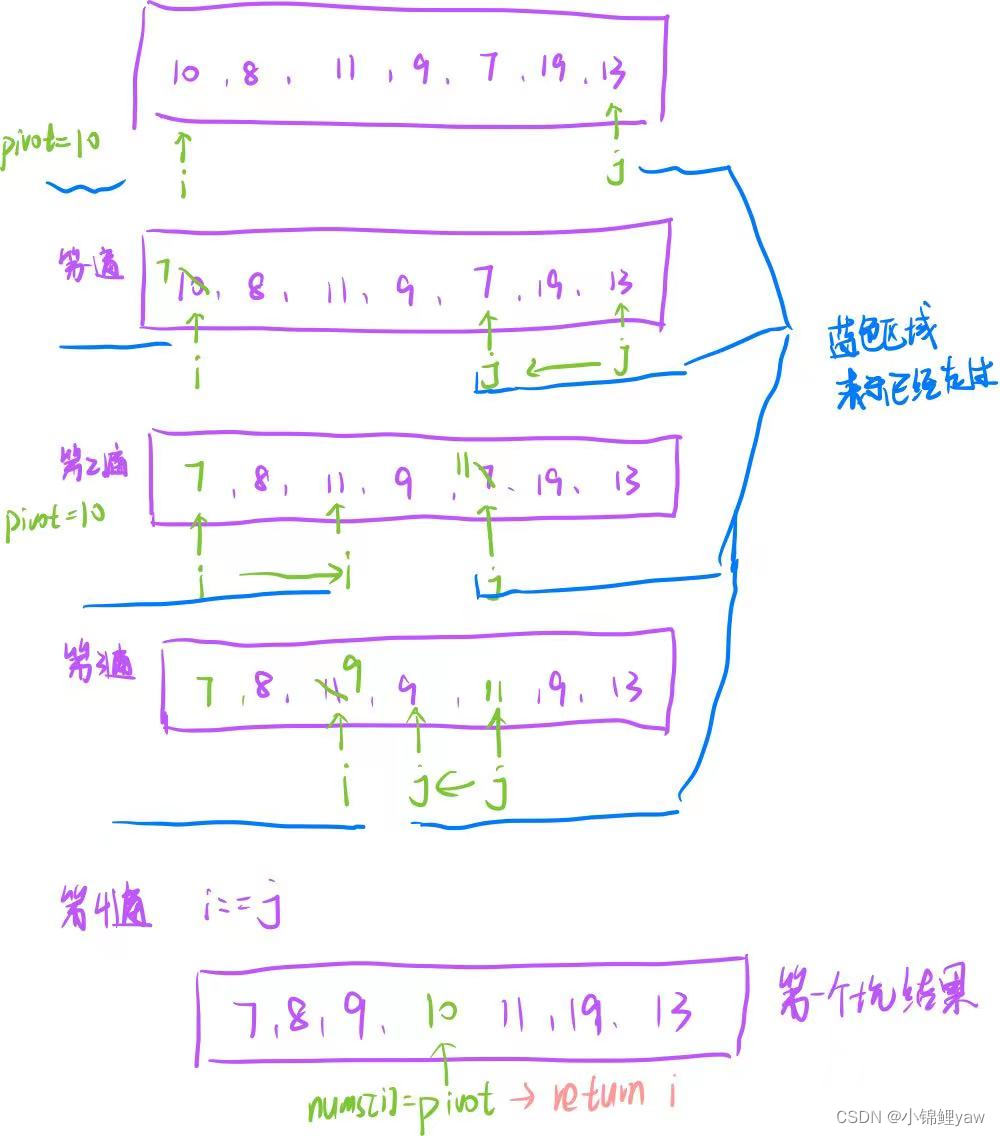
快速排序和直接选择排序不同的是在快排选择的过程中在不断地调整元素的顺序,在这个过程中原数组已经不断有序了
2.详细代码
/*** 快速排序(挖坑法)*/public static void quitSort(int[] nums) {quitSortInternal(nums, 0, nums.length-1);}private static void quitSortInternal(int[] nums, int l, int r) {if (l >= r) {return;}// 分区之后,返回已经放好位置的元素下标int p = quitSortByHole(nums, l, r);// 将放好位置元素的左侧丢进去排序quitSortInternal(nums, l, p - 1);// 在将放好位置元素的右侧丢进去排序quitSortInternal(nums, p + 1, r);// 此时数组就整体有序了}/*** 使用非递归的方式* @param nums* @param l* @param r*/private static void quitSortInternal1(int[] nums, int l, int r) {Deque<Integer> stack = new ArrayDeque<>();stack.push(r);stack.push(l);while (!stack.isEmpty()) {// 获取左右区间int i = stack.pop();int j = stack.pop();if (i >= j) {continue;}// 调用获得一个位置的结果int p = quitSortByHole(nums, i, j);// 将左边压入栈中stack.push(p-1);stack.push(i);// 右边压入栈中stack.push(j);stack.push(p+1);}}private static int quitSortByHole(int[] nums, int l, int r) {// 分区数字int pivot = nums[l];int i = l;int j = r;while (i < j) {while (i < j && nums[j] >= pivot) {j--;}// 走到这说明nums[j] < pivotnums[i] = nums[j];while (i < j && nums[i] <= pivot) {i++;}// 走到这说明nums[i] > pivotnums[j] = nums[i];}// 出循环说明i==j// 将pivot写回inums[i] = pivot;// 返回分区点最终位置return i;}
4.归并排序
⭐归并排序(稳定,时间复杂度O(nlogn),空间复杂度O(n))
对原始数据不敏感
1.核心思路
1. 先不断地将原数组一分为二,直至子数组长度为1
2. 不断地将两个相邻的有序子数组合并成一个更大的有序子数组,直至合并后的数组与原数组长度相同,此时排序完成
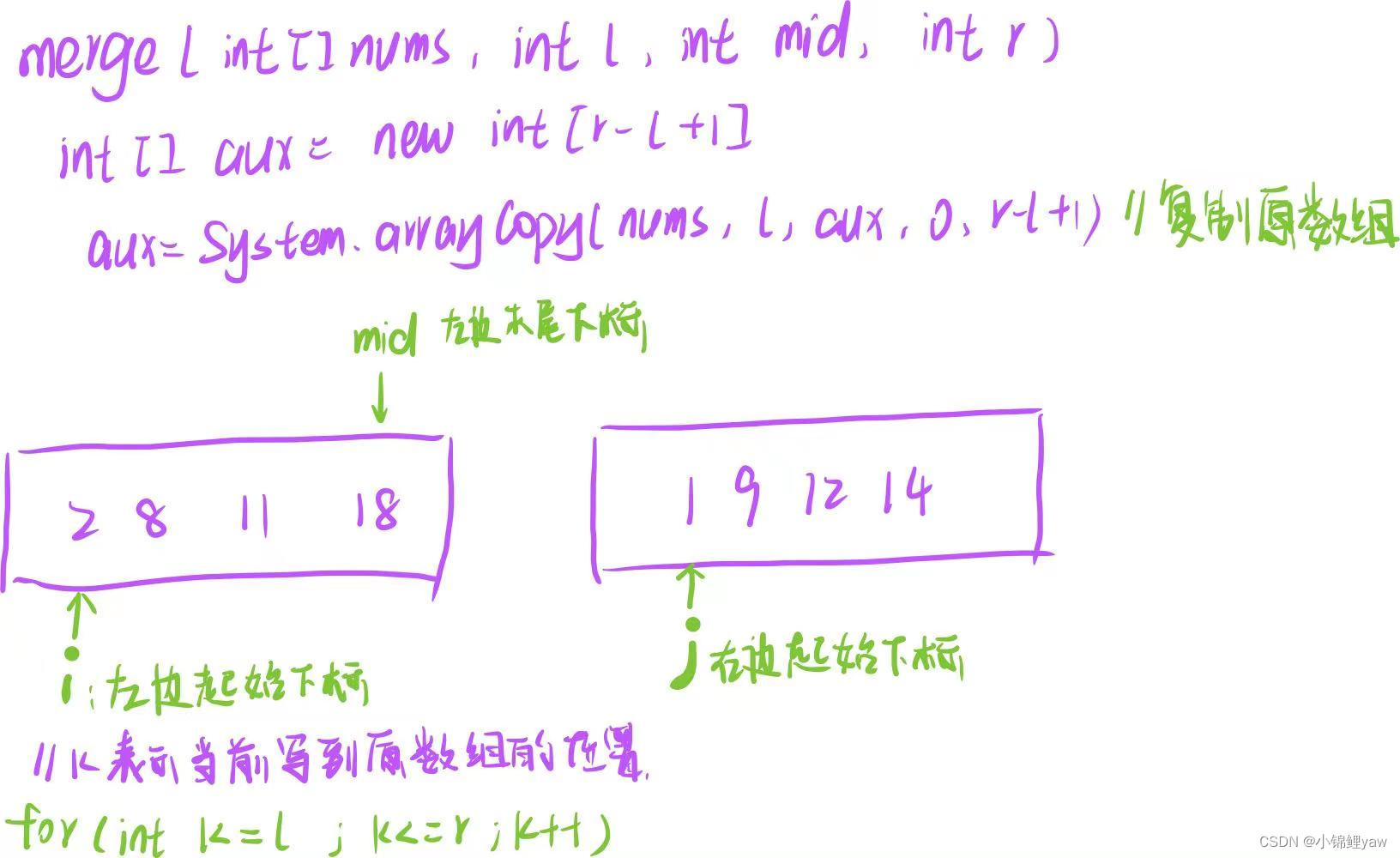
核心操作:合并两个子数组merge(nums, l, mid, r)
int i=l代表左边数组走到的下标,
int j=mid+1代表右边数组走到的下标,
k代表当前原数组合并到哪个位置
2.归并排序应用

3.详细代码
/*** 归并排序*/public static void mergeSort(int[] nums) {mergeSortInternal(nums, 0, nums.length-1);}/*** 在nums的l-r内进行归并排序* @param nums* @param l* @param r*/private static void mergeSortInternal(int[] nums, int l, int r) {if (l >= r) {return;}int mid = l + ((r - l) >> 1);;// 将左边和右边丢到mergemergeSortInternal(nums, l, mid);mergeSortInternal(nums, mid+1, r);// 此时说明左右两个数组都已经排好序merge(nums, l, mid, r);}private static void merge(int[] nums, int l, int mid, int r) {// 创建一个大小与r-l+1一样大的数组int[] aux = new int[r - l + 1];System.arraycopy(nums, l, aux, 0, r - l + 1);int i = l;int j = mid+1;// i代表左边数组走到的下标,j代表右边数组走到的下标,k代表当前原数组合并到哪个位置for (int k = l; k <= r; k++) {if (i > mid) {// 说明左边的数组已经走完,把右边的全部写回原数组即可nums[k] = aux[j-l];j++;} else if (j > r) {// 说明右边的数组已经走完,把左边的全部写回原数组即可nums[k] = aux[i-l];i++;} else if (aux[i-l] <= aux[j-l]) {// 说明左边的数字小,把左边数组内的数字写回原数组nums[k] = aux[i-l];i++;} else {// 说明右边的数字小,把右边数组内的数字写回原数组nums[k] = aux[j-l];j++;}}}
相关文章:

七大排序算法详解
1.概念 1.排序的稳定性 常见的稳定的排序有三种:直接插入排序,冒泡排序,归并排序 对于一组数据元素排列,使用某种排序算法对它进行排序,若相同数据之间的前后位置排序后和未排序之前是相同的,我们就成这种…...
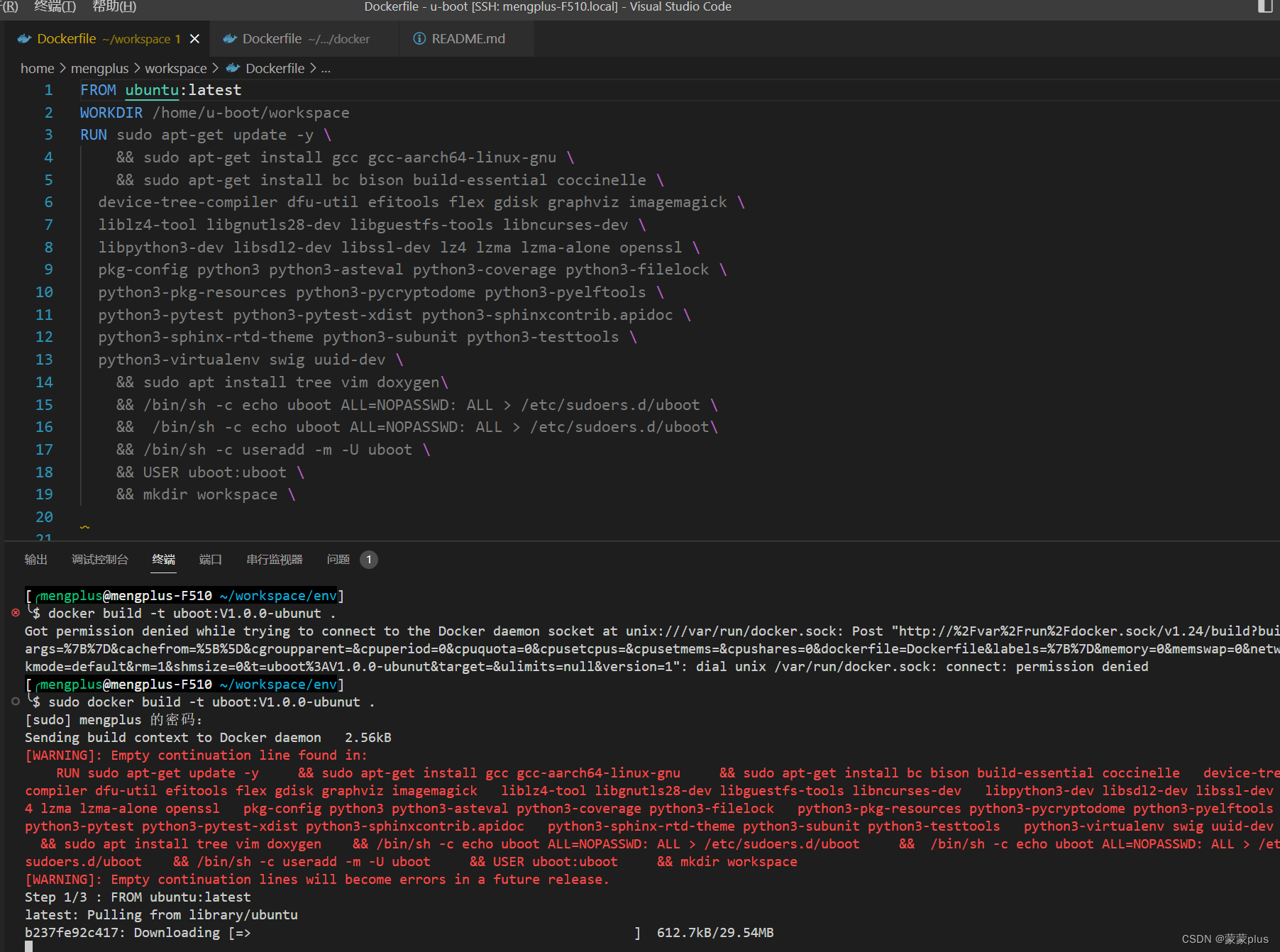
[docker][WARNING]: Empty continuation line found in:
报警内容: 下面展示一些 内联代码片。 //执行 sudo docker build ubuntu:v1.00 . [WARNING]: Empty continuation line found in:出现上述错误原因为18行多了一个 " \" 符号,去除即可...

探工业互联网的下一站!腾讯云助力智造升级
引言 数字化浪潮正深刻影响着传统工业形态。作为第四次工业革命的重要基石,工业互联网凭借其独特的价值快速崛起,引领和推动着产业变革方向。面对数字化时代给产业带来的机遇与挑战,如何推动工业互联网的规模化落地,加速数字经济…...

SpringBoot上传文件的实现与优化
一、什么是文件上传? 文件上传是指客户端将本地的文件通过HTTP协议发送到服务器端的过程。文件上传是Web开发中常见的功能之一,例如用户可以上传头像、照片、视频、文档等各种类型的文件。文件上传涉及到客户端和服务器端的交互,需要考虑文件…...

学习python可以做什么?有前景么
Python被热门领域广泛应用 学习者就业优势明显! 说到Python的优势,就不得不提这句玩笑话:Python除了不会生孩子,其他的都会。 Web开发、网络爬虫、数据分析、人工智能、自动化、云计算、网络编程、游戏开发等领域,统…...

还不知道怎么提示LLM?ChatGPT提示入门
文章目录 简介:什么是人工智能?什么是提示过程?为什么会出现这样的差异? 为什么需要提示过程?1) 文章摘要2) 数学问题求解 如何进行提示过程?角色提示:多范例提示:无范例提示单范例提…...
反射机制-体会反射的动态性案例(尚硅谷Java学习笔记)
// 举例01 public class Reflect{ // 静态性 public Person getInstance(){return new Person(); }// 动态性 public T<T> getInstance(String className) throws Exception{Calss clzz Class.forName(className);Constructor con class.getDeclaredConstructor();con…...
uniapp离线打包apk - Android Studio
uniapp 离线打包 基于uni-app的andiord 离线打包 开发工具及所需要的jar包1.将下载的App离线SDK解压打开,找到HBuilder-Integrate-AS ,在Android Studio打开2.打开HBuilder X,发行->原生app本地打包->生成本地打包app资源3.在“HBuil…...

cuda面试准备(一),架构调试
1 cuda架构 硬件方面 SP (streaming Process) ,SM (streaming multiprocessor) 是硬件(GPUhardware) 概念。而thread,block,grid,warp是软件上的(CUDA) 概念 SP:最基本的处理单元,streaming processor,也称为CUDA core,最后具体的指令和任务都是在SP上处理的。GPU进行并行…...

docker containers logs清理
容器的磁盘占用 每次创建一个容器时,都会有一些文件和目录被创建,例如: /var/lib/docker/containers/ID目录,如果容器使用了默认的日志模式,他的所有日志都会以JSON形式保存到此目录下。 /var/lib/docker/overlay2 目…...

Ubuntu安装RabbitMQ
一、安装 更新系统软件包列表: sudo apt update安装RabbitMQ的依赖组件和GPG密钥: sudo apt install -y curl gnupg curl -fsSL https://github.com/rabbitmq/signing-keys/releases/download/2.0/rabbitmq-release-signing-key.asc | sudo gpg --dearmo…...

Vue3获取当前环境信息
获取.env.development和.env.production内的信息及环境信息 在业务逻辑文件中可以通过 import.meta.env的方式获取,例如: const { MODE, VITE_APP_BASE_API} import.meta.env在vite.config.js中获取: import { defineConfig, loadEnv } f…...

Linux 系统 diff 文件比较命令详解
diff 命令用于比较两个文件或目录之间的差异。它会逐行比较文件的内容,并且在不同的行上显示不同之处。下面是 diff 命令的使用方法和选项: 基本语法: diff [选项] 文件1 文件2常见选项: -c 或 --context:显示上下文…...
【负载均衡】Nacos简单入门
Nacos简单入门 快速安装 在Nacos的GitHub页面,提供有下载链接,可以下载编译好的Nacos服务端或者源代码: 下载完压缩包之后,放在任意目录下面进行解压: GitHub主页:https://github.com/alibaba/nacos G…...
实验一 ubuntu 网络环境配置
ubuntu 网络环境配置 【实验目的】 掌握 ubuntu 下网络配置的基本方法,能够通过有线网络连通 ubuntu 和开发板 【实验环境】 ubuntu 14.04 发行版FS4412 实验平台 【注意事项】 实验步骤中以“$”开头的命令表示在 ubuntu 环境下执行,以“#”开头的…...

ubuntu can应用开发环境搭建指南
sudo apt-get update sudo apt-get install can-utils libsocketcan-dev can数据发送这个采用来自网上的一段代码进行测试: can_send.c代码内容如下: /* 1. 报文发送程序 */ #include <stdio.h> #include <stdlib.h> #include <string.h> #include <…...

全流程R语言Meta分析核心技术高阶应用
查看原文>>>全流程R语言Meta分析核心技术高阶应用 目录 专题一、Meta分析的选题与检索 专题二、Meta分析与R语言数据清洗及统计方法 专题三、R语言Meta分析与作图 专题四、R语言Meta回归分析 专题五、R语言Meta诊断分析 专题六、R语言Meta分析的不确定性 专题…...

windows下安装使用git-lfs克隆大文件
下载安装git-lfs工具 首先去git-lfs这里,下载相应平台的工具,我下载的windows版本,非安装版本,直接配置到系统环境变量里 执行以下命令验证是否成功 git lfs install 克隆数据集 这样自动会下载里边的大文件 git clone https:/…...
Node.js下载安装及环境配置教程
一、进入官网地址下载安装包 https://nodejs.org/zh-cn/download/ 选择对应你系统的Node.js版本,这里我选择的是Windows系统、64位 Tips:如果想下载指定版本,点击【以往的版本】,即可选择自己想要的版本下载 二、安装程序 &a…...

半导体低压热氧工艺中的真空度精密控制解决方案
摘要:在目前的各种半导体材料热氧化工艺中,往往需要对正负压力进行准确控制并对温度变化做出快速的响应,为此本文提出了热氧化工艺的正负压力控制解决方案。解决方案的核心是基于动态平衡法分别对进气和排气流量进行快速调节,具体…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
