【数据结构】回溯算法公式化解题 leetcode经典题目带刷:全排列、组合、子集
目录
- 回溯算法
- 一、什么是回溯算法
- 1、基本思想:
- 2、一般步骤:
- 二、题目带练
- 1、全排列
- 2、组合
- 3、子集
- 三、公式总结
回溯算法
一、什么是回溯算法
回溯算法(Backtracking Algorithm)是一种解决组合问题、排列问题、选择问题等一类问题的常用算法。它通过尝试所有可能的选择来找到问题的解,当发现当前选择不符合要求时,就回溯到之前的状态,然后尝试其他的选择。
1、基本思想:
- 从问题的起始点开始,进行尝试,每次选择一个可能的路径。
- 如果发现当前选择无法达到解决问题的目标,就回退到上一个状态,尝试其他的选择。
- 不断地重复上述过程,直到找到解决问题的路径,或者遍历完所有可能的选择。
2、一般步骤:
- 确定问题的解空间和约束条件。
- 从解空间中选择一个可能的选择,进入下一步。
- 判断当前选择是否符合约束条件,如果符合,继续深入尝试下一步;如果不符合,回退到上一步。
- 重复上述步骤,直到找到解,或者遍历完所有可能的选择。
二、题目带练
1、全排列
题目地址
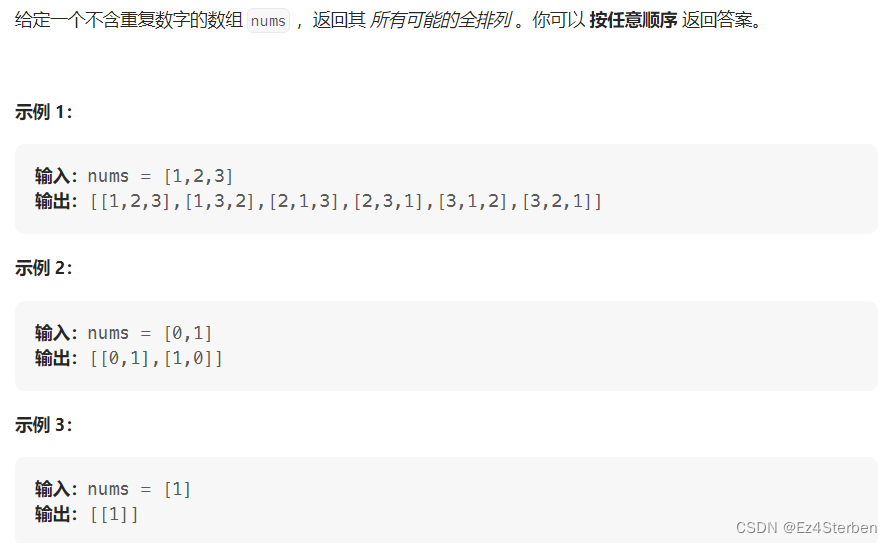
分析:
看到这道题的描述,不难想到,如果我们要找出所有的排列方式,就要遍历n次数组,每次选择一个不重复元素排列在上次循环选择的元素后面,那这就出现了一个问题:怎么对一个数组遍历n次?
显然这是不太可能实现的,因为n是不确定的,但是我们可以换一种思路,通过深度来代表遍历次数,也就是我们常说的回溯算法。
根据题意,我们应当设递归出口为 当前递归的深度 == 数组的长度if(depth == nums.length),同时保存当前的排列方式到集合中。ans.add(new ArrayList<>(path));每次递归的过程中我们需要遍历一次数组for(int i = 0; i < nums.length; i++),判断当前的元素是否被使用过if(used[i]),如果没被使用那么就将其记录下来,并且标记为使用过,继续进入递归path.add(nums[i]); used[i] = true;。当这次递归结束时dfs(nums,depth + 1,used);,撤销当前元素的使用标记,并且移除记录的集合。path.remove(path.size() - 1); used[i] = false;
效果就是调用方法后,先选择元素1path.add(nums[0]); used[0] = true;,再次调用方法记录深度+1dfs(nums,depth + 1,used);,此时发现1已经被选择过了,开始选择2path.add(nums[1]); used[1] = true;,调用递归,深度+1dfs(nums,depth + 1,used);,同理1,2被标记为使用过的元素,继续选择3path.add(nums[2]); used[2] = true;,然后递归结束。这里会退回到深度为2的那次选择,因为2之后还有别的元素可以选择,选择3后发现只有2可以选了,首选项为1的递归结束,依次类推得到所有排列方式。
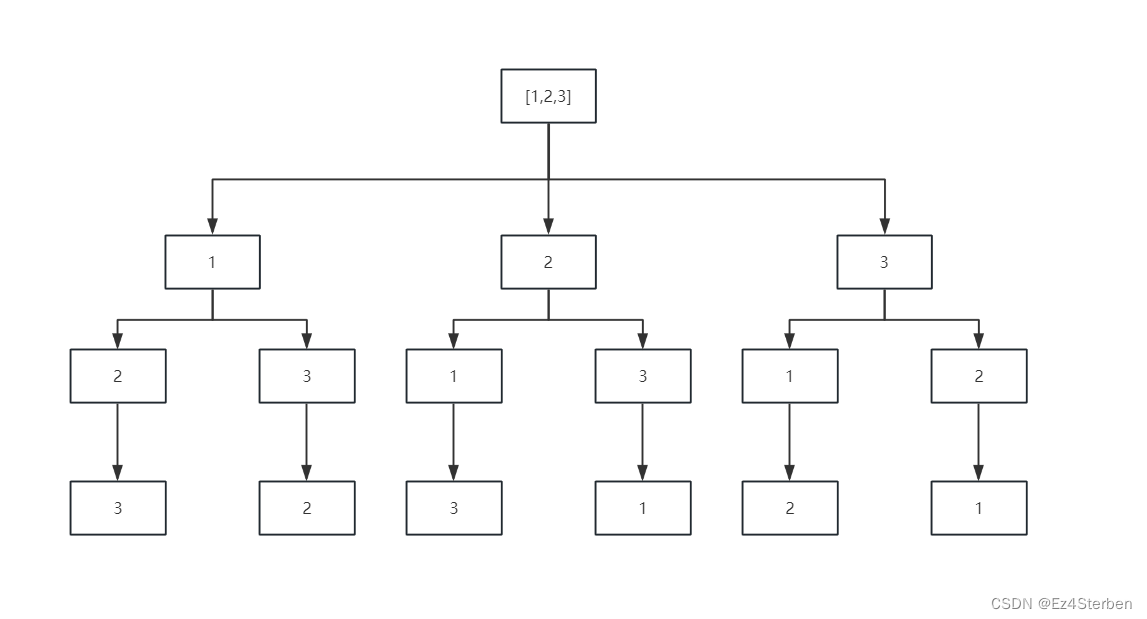
代码如下:
class Solution {public List<List<Integer>> ans = new ArrayList<>();public List<Integer> path = new ArrayList<>();public List<List<Integer>> permute(int[] nums) {boolean[] used = new boolean[nums.length];dfs(nums,0,used);return ans;}public void dfs(int[] nums,int depth,boolean[] used){if(depth == nums.length){ans.add(new ArrayList<>(path));return;}for(int i = 0; i < nums.length; i++){if(used[i]){continue;}path.add(nums[i]);used[i] = true;dfs(nums,depth + 1,used);path.remove(path.size() - 1);used[i] = false;}}
}
2、组合
题目地址

分析:
这道题与全排列的区别在于,全排列需要全部选择,而这道题不一定要全部选择,并且每个组合只能有一次,所以面对这道题,我们不能按照和之前同样的思路去解,因为无法排除同样组合的组合顺序问题。
那么我们要如何作出改动呢?
其实很简单,我们只需要让每次循环的起始值变为当前的深度即可,同时也不需要判断是否使用过了,因为我们只会向后找,不会从前开始往后找了。
class Solution {List<Integer> temp = new ArrayList<Integer>();List<List<Integer>> ans = new ArrayList<List<Integer>>();public List<List<Integer>> combine(int n, int k) {dfs(1, n, k);return ans;}public void dfs(int depth, int n, int k) {if (temp.size() == k) {ans.add(new ArrayList<Integer>(temp));return;}for(int i = depth;i <= n;i++){temp.add(i);dfs(i + 1, n, k);temp.remove(temp.size() - 1);}}
}
3、子集
题目地址

分析:
大家看这道题可能会发现,是不是和组合有点相似?区别在哪呢,区别在于子集的选择长度不一定是n,而是[0,n]。
其实我们只需要每次回溯都记录一次结果就好了。
class Solution {List<Integer> list = new ArrayList<>();List<List<Integer>> result = new ArrayList<>();public List<List<Integer>> subsets(int[] nums) {dfs(0,nums);return result;}public void dfs(int current, int[] nums){result.add(new ArrayList<>(list));if(current == nums.length){return;}for(int i = current; i < nums.length; i++){list.add(nums[i]);dfs(i + 1, nums);list.remove(list.size() - 1);}}
}
三、公式总结
如果认真看完的朋友可以发现,对于这种基础的回溯题目,我们都可以通过循环+回溯来解决问题,只需要根据具体问题来更改我们的循环条件即可。
当然这么做不一定是最好的,还有许多可以优化的地方,只是说大部分情况可以通过这种循环的方式来解决问题。
相关文章:

【数据结构】回溯算法公式化解题 leetcode经典题目带刷:全排列、组合、子集
目录 回溯算法一、什么是回溯算法1、基本思想:2、一般步骤: 二、题目带练1、全排列2、组合3、子集 三、公式总结 回溯算法 一、什么是回溯算法 回溯算法(Backtracking Algorithm)是一种解决组合问题、排列问题、选择问题等一类问…...

WPF基础入门-Class3-WPF数据模板
WPF基础入门 Class3:WPF数据模板 1、先在cs文件中定义一些数据 public partial class Class_4 : Window{public Class_4(){InitializeComponent();List<Color> test new List<Color>();test.Add(new Color() { Code "Yellow", Name &qu…...

js将搜索的关键字加颜色
js将搜索的关键字加颜色 使用正则匹配关键字并加入span标签,页面渲染时使用v-html渲染即可 // 文本框内容 let searchCont 测试;const reg new RegExp((${searchCont.value}), g); let data 图片保存测试A; data data.replace(reg, <span style"color:…...

Docker安装Oracle数据库打开、链接速度很慢
问题: 使用Docker安装Oracle数据库打开、链接速度很慢,明显的在在转圈严重影响效率。 解决: 排查到DNS时,发现宿主机DNS配置清空后,通过JDBC连接目标Oracle数据库速度很快 进入容器中进行测试,发现清空DNS…...
学生分班查询系统的创建与使用指南
开学季,负责分班工作的老师们又面临一个难题:如何公布分班结果?将结果放在学校官网上可能会让很多无关人员看到,而不放则会导致家长们纷纷打电话来询问。那么,有没有一种方法可以让家长们自行查看分班结果呢࿱…...

全套解决方案:基于pytorch、transformers的中文NLP训练框架,支持大模型训练和文本生成,快速上手,海量训练数据!
全套解决方案:基于pytorch、transformers的中文NLP训练框架,支持大模型训练和文本生成,快速上手,海量训练数据! 1.简介 目标:基于pytorch、transformers做中文领域的nlp开箱即用的训练框架,提…...

ffmpeg
文章目录 libavcodec实现 libavformat实现libavfilter实现 libswscale实现对比libavfilter图像处理libswscale vs libyuvlibavutil 命令行工具ffmpeg例子 ffprobe例子 FFmpeg 是一个由 C 语言编写的开源跨平台音视频处理工具集,它具有模块化的架构。下面是 FFmpeg 的…...
)
CH03_代码的坏味道(下)
循环语句(Loops) 从最早的编程语言开始,循环就一直是程序设计的核心要素。如今,函数作为一等公民已经得到了广泛的支持,因此我们可以使用以管道取代循环(231)管道操作(如filter和ma…...

journal日志导致服务器磁盘满
背景 ubuntu 18.04服务器磁盘突然100% 一查/var/log/journal目录占了14G 清理 要清理 journal 日志,可以使用以下步骤: 运行以下命令来查看 journal 日志的使用情况: journalctl --disk-usage这将显示 journal 日志的当前使用情况&#x…...

“Go程序员面试笔试宝典”复习便签
一.逃逸分析 1.1逃逸分析是什么? 逃逸分析,主要是Go编译器用来决定变量分配在堆或者栈的手段。 区分于C/C手动管理内存分配,Go将这些工作交给了编译器。 1.2逃逸分析有什么作用 解放程序员。程序员不需要手动指定指针分配内存。 灵活的…...
)
数组的度(指数组里任一元素出现频数的最大值)
题目: 给定一个非空且只包含非负数的整数数组 nums,数组的 度 的定义是指数组里任一元素出现频数的最大值。 你的任务是在 nums 中找到与 nums 拥有相同大小的度的最短连续子数组,返回其长度。 示例 1: 输入:nums …...

scala array类型参数
在Scala中,数组(Array)是一种用于存储相同类型元素的数据结构。数组可以用于保存基本数据类型和自定义数据类型的元素。当定义数组类型参数时,您通常是在函数、类或方法签名中使用它们。以下是一些有关Scala数组类型参数的示例&am…...
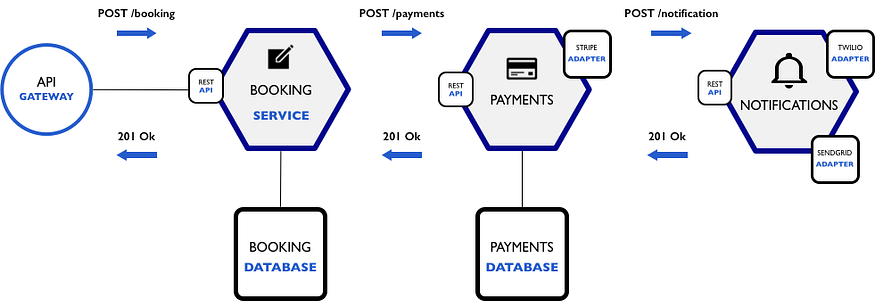
构建 NodeJS 影院预订微服务并使用 docker 部署(03/4)
一、说明 构建一个微服务的电影网站,需要Docker、NodeJS、MongoDB,这样的案例您见过吗?如果对此有兴趣,您就继续往下看吧。 你好社区,这是🏰“构建 NodeJS 影院微服务”系列的第三篇文章。本系列文章演示了…...

html写一个向flask_socketio发送消息和接收消息并显示在页面上
以下是一个简单的HTML页面,它包含一个输入框、一个发送按钮和一个显示区域。用户可以在输入框中输入消息,点击发送按钮,然后这个消息会被发送到 Flask-SocketIO 服务器。当服务器回应消息时,它会在页面的显示区域显示出来。 <…...

C#使用.Net Core进行跨平台开发
使用 .NET Core 进行跨平台开发是一种灵活的方法,可以在多个操作系统上运行 C# 应用程序。以下是在 C# 中使用 .NET Core 进行跨平台开发的一般步骤: 安装 .NET Core SDK: 在开始之前,需要安装适用于操作系统的 .NET Core SDK。可…...

Java“牵手”天猫店铺所有商品API接口数据,通过店铺ID获取整店商品详情数据,天猫API申请指南
天猫商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。天猫商品详情可以帮助消费者更好的了解宝贝信息,从而做出购买决策。同时,消费者也可以通过商品详情了解其他买家对宝贝的评价…...

php输入post过滤函数,入库出库,显示
第一部分 php输入post过滤函数 function GLOBAL_POST($str) {$str_origin$str; if (empty($str)) return false;$str str_replace( /, "", $str);//替换关键词 $str str_replace("\\", "", $str); $str str_replace(">", &…...
matlab-对数据集加噪声并实现tsne可视化
matlab-对数据集加噪声并实现tsne可视化 最近才知道,原来可以不用模型,也能实现对数据集数据的可视化。 **一、**以COIL-100数据集为例子。 问题: 前提:首先对COIL-100数据集根据角度0-175和180-255,分别划分成C1,C…...
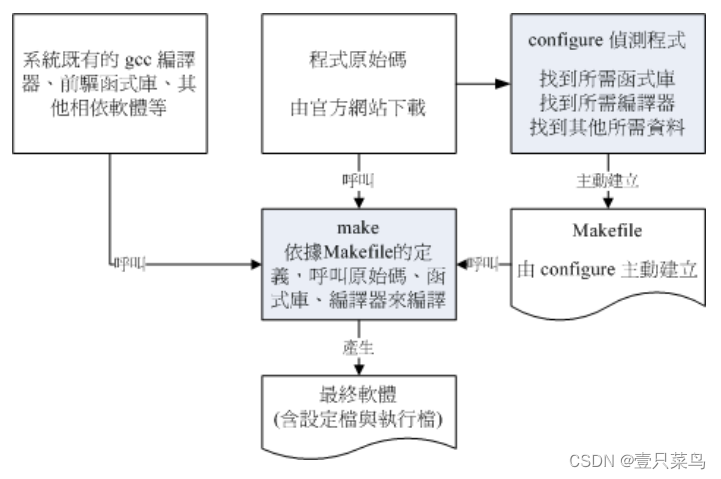
【BASH】回顾与知识点梳理(三十八)
【BASH】回顾与知识点梳理 三十八 三十八. 源码概念及简单编译38.1 开放源码的软件安装与升级简介什么是开放源码、编译程序与可执行文件什么是函式库什么是 make 与 configure什么是 Tarball 的软件如何安装与升级软件 38.2 使用传统程序语言进行编译的简单范例单一程序&#…...

Sql注入攻击的三种方式
SQL注入是指web应用程序对用户输入数据的合法性没有判断或过滤不严,攻击者可以在web应用程序中事先定义好的查询语句的结尾上添加额外的SQL语句,在管理员不知情的情况下实现非法操作,以此来实现欺骗数据库服务器执行非授权的任意查询,从而进一步得到相应的数据信息。SQL 注…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...
