【核磁共振成像】方格化重建
目录
- 一、缩放比例
- 二、方格化变换的基础
- 三、重建时间
- 四、方格化核
一、缩放比例
对于笛卡尔K空间直线轨迹数据可直接用FFT重建,而如果K空间轨迹的任何部分都是非均匀取样的 可用DFT直接重建,有时称为共轭相位重建,但此法太慢不实用。把数据再取样到直线格使能FFT重建要快得多。普遍应用的内插方法是把数据与一个平滑函数卷积再取样,这个 重建过程(包括FFT) 被称为 方格化。
方格化在K空间中用一个卷积转换输入数据到一个均匀直线格数据集,因自选密度本身是紧支的(即有限区域外都是零),只要测量值是大于或等于奈奎斯特频率采样的,任意位置的K空间值都可以被测量值的sinc内插精确计算(即测量的K空间值与sinc函数卷积)。
sinc内插的缺点是sinc函数不是紧支的。因此,在每个新K空间位置计算K空间值,要求sinc函数被所有测量的数据乘,导致比较长的计算时间。
在方格化中,sinc函数被一个紧支函数(方格化核)取代以节省计算时间。K空间数据与方格化核卷积等价于图像被核的FT乘。
sinc卷积方格化导致些许图像质量损失,因为再取样卷积的K空间导致一个带有混叠的图像。通常通过K空间过取样以增大FOV(把直线混叠的复制进一步推离开推向),以降低混叠,然后在FT后放弃额外的FOV。

左为模拟的spiral扫描图像,显示有混叠伪影。
混叠延申到无限远,即使显示的截面有限(方框是扫描中指定的FOV)。
右为从左图(尚无直线再取样)的K空间数据的内插产生的图像
如果对应于左图的K空间数据与一紧支函数而不是sinc卷积,混叠伪影就不会被截去。
径向投影MR数据也可以用CT中常用的滤波背投影算法,但此法在MRI中不受欢迎。对一个离散数据集再取样问题已经发展了许多方法,直接内插会导致伪影,基于卷积的方法比如方格化在MRI中被广泛使用,因为它比其他方法快,并且能给出足够好的图像质量。
所谓 两个函数的卷积,本质上就是先将一个函数翻转,然后进行滑动叠加。在连续情况下,叠加指的是对两个函数的乘积求积分,在离散情况下就是加权求和,为简单起见就统一称为叠加。卷积的“卷”,指的的函数的翻转,从 g(t) 变成 g(-t) 的这个过程;同时,“卷”还有滑动的意味在里面。如果把卷积翻译为“褶积”,那么这个“褶”字就只有翻转的含义了。卷积的“积”,则指的是积分/加权求和。
以信号分析为例,卷积的结果是不仅跟当前时刻输入信号的响应值有关,也跟过去所有时刻输入信号的响应都有关系,考虑了对过去的所有输入的效果的累积。在图像处理中,卷积处理的结果,其实就是把每个像素周边的,甚至是整个图像的像素都考虑进来,对当前像素进行某种加权处理。所以说,“积”是全局概念,或者说是一种“混合”,把两个函数在时间或者空间上进行混合。
进行“卷”(翻转)的目的其实是施加一种约束,它指定了在“积”的时候以什么为参照。在信号分析的场景,它指定了在哪个特定时间点的前后进行“积”,在空间分析的场景,它指定了在哪个位置的周边进行累积处理。
二、方格化变换的基础
方格化所需要的步骤为:
(1)对各个输入数据点计算K空间位置和密度补偿。
(2)计算方格化核及其反傅里叶变换,存储方格化核作为一个查找表或者对各个输入、输出数据样本存储值。
(3)如果需要,从输入数据减去基线。
(4)准备一个待输出K空间矩阵,对各个输入数据样本在输入点的紧支距离内找出所有均匀直线输出位置。
(5)应用一个K空间窗和符号交替到再取样的直线K空间数据上。
(6)反傅里叶变换均匀直线再取样的K空间数据上。
(7)如果K空间过取样用于降低混叠,提取图像的中间位置相应于所希望的最终FOV。
(8)用方格化核的反傅里叶变换除以中间像。
(9)如果需要实像或虚像,进行符号交替。
(10)计算最终图像,比例缩放。
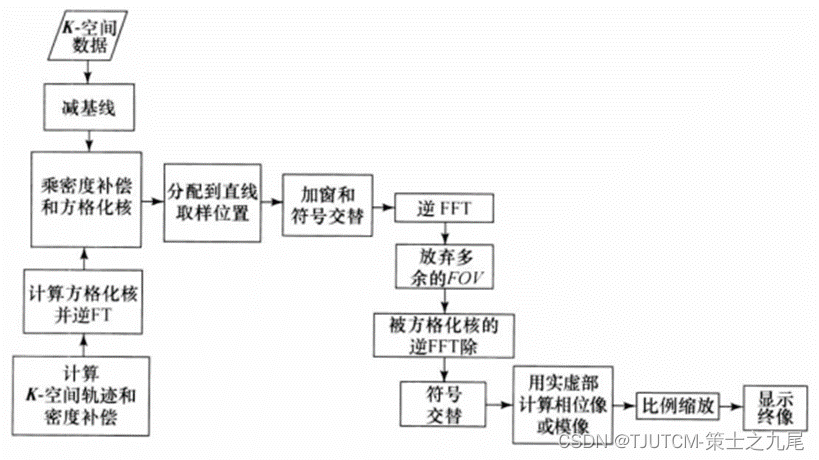
方格化是一个局部过程,只需在原取样点附近执行。
为了节省计算时间,方格化核值通常不再对各个输出点计算。方格化核值只对相对小数量点计算,比如256点,并存在一个查找表中。如果同样的K空间轨迹用于重复的重建,并且有足够多存储器的话,第一个像之后所有像的重建时间可通过查表而大大节省。
三、重建时间
方格化重建 可分为三步:卷积、FFT和被方格化核的IFT除。
卷积步乘法运算次数 是输入数据样本数Ns乘以位于各输入样本的距离w内的均匀直线位置数。如果w是用均匀直线样本的单位给定的,乘运算次数对于1D方格化是wNs,对2D方格化是w^2Ns,以此类推。
例如 在傅里叶变换中,一个复数函数的实部和虚部分别对应着信号的振幅和相位。如果一个信号的傅里叶变换F(k)的共轭F*(k)等于F(-k),那么这个信号的相位是对称的,即F(k)和F*(k)相位相等。相位信息可以用来描述信号的时间演化和频率成分。
受敲击的鼓面振幅沿半径方向的分布就是一个贝塞尔函数(考虑正负号)。实际上,这些振动是各阶贝塞尔函数的叠加。
根据图像阵列的特性,对其按下列步骤进行FFT变换:
(1)将图像数据阵列变换为按列存储,即从下到上,从左到右;
(2)对每一列图像数据进行1-D FFT;
(3)将按列处理后的数据结果存储,并对它们按原图像阵列的形式,即按行重新存储;
(4)对重新排列的数据逐行进行1-D FFT;
(5)将每行处理后的数据存储起来,即得到2-D 数字图像FFT结果。
关于离散傅里叶变换变换:
(1)实数信号变换的结果X[k]是一组复数,里面一半数据和另一半是共轭的。意味着N点DFT,只有N/2的数据是含有有用信息的。
(2)用DFT的结果如何做频谱分析,即在采样频率为fs的情况下, x[n]的n只是一个离散的数值。
四、方格化核
最佳1D方格化核g(K)是Kaiser-Bessel函数,在终像最逼近理想像(例如用共轭相位重建)的意义上说,Kaiser-Bessel函数作为方格化核能给出最佳结果。
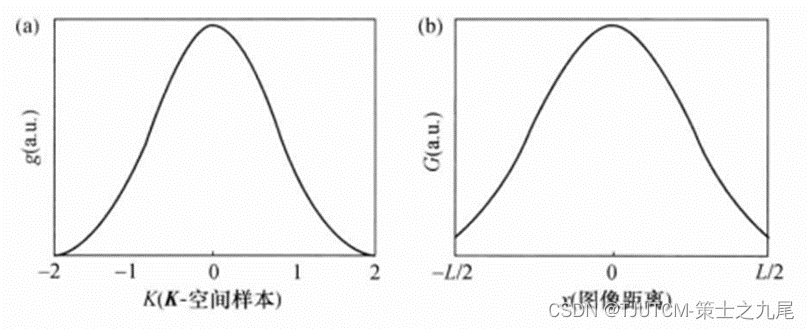
(a)图为Kaiser-Bessel函数(任意单位)作为K空间距离(以K空间为单位)的函数
(b)图为Kaiser-Bessel函数(任意单位)的反傅里叶变换曲线作为图像视野L的函数,Kaiser-Bessel函数参数w=4,b=8
相关文章:

【核磁共振成像】方格化重建
目录 一、缩放比例二、方格化变换的基础三、重建时间四、方格化核 一、缩放比例 对于笛卡尔K空间直线轨迹数据可直接用FFT重建,而如果K空间轨迹的任何部分都是非均匀取样的 可用DFT直接重建,有时称为共轭相位重建,但此法太慢不实用。把数据再…...

JAVA中时间戳和LocalDateTime的互转
时间戳转LocalDateTime: 要将时间戳转换为LocalDateTime并将LocalDateTime转换回时间戳,使用Java的java.time包。以下是示例代码: import java.time.Instant; import java.time.LocalDateTime; import java.time.ZoneId;public class Times…...

无涯教程-进程 - 创建终止
到现在为止,我们知道无论何时执行程序,都会创建一个进程,并且该进程将在执行完成后终止,如果我们需要在程序中创建一个进程,并且可能希望为其安排其他任务,该怎么办。能做到吗?是的,显然是通过…...
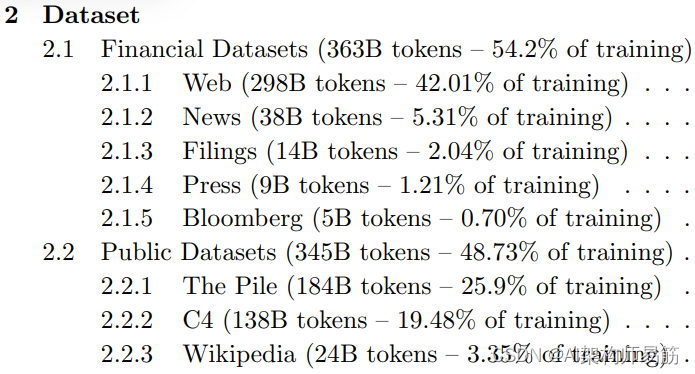
LLMs参考资料第一周以及BloombergGPT特定领域的训练 Domain-specific training: BloombergGPT
1. 第1周资源 以下是本周视频中讨论的研究论文的链接。您不需要理解这些论文中讨论的所有技术细节 - 您已经看到了您需要回答讲座视频中的测验的最重要的要点。 然而,如果您想更仔细地查看原始研究,您可以通过以下链接阅读这些论文和文章。 1.1 Trans…...

LeetCode字符串数组最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。 如果不存在公共前缀,返回空字符串 “”。 示例 1: 输入:strs [“flower”,“flow”,“flight”] 输出:“fl” 示例 2: 输入:strs [“dog”,“raceca…...
Git gui教程---第八篇 Git gui的使用 创建一个分支
一般情况下一个主分支下代码稳定的情况下会新建出一个分支,然后在分支上修改,修改完成稳定后再合并到主分支上。 或者几个人合作写一份代码,每个人各一个分支,测试稳定再合并到主分支上。 在git gui选择菜单栏“分支”࿰…...
Docker修改daemon.json添加日志后无法启动的问题
docker实战(一):centos7 yum安装docker docker实战(二):基础命令篇 docker实战(三):docker网络模式(超详细) docker实战(四):docker架构原理 docker实战(五):docker镜像及仓库配置 docker实战(六):docker 网络及数据卷设置 docker实战(七):docker 性质及版本选择 认知升…...
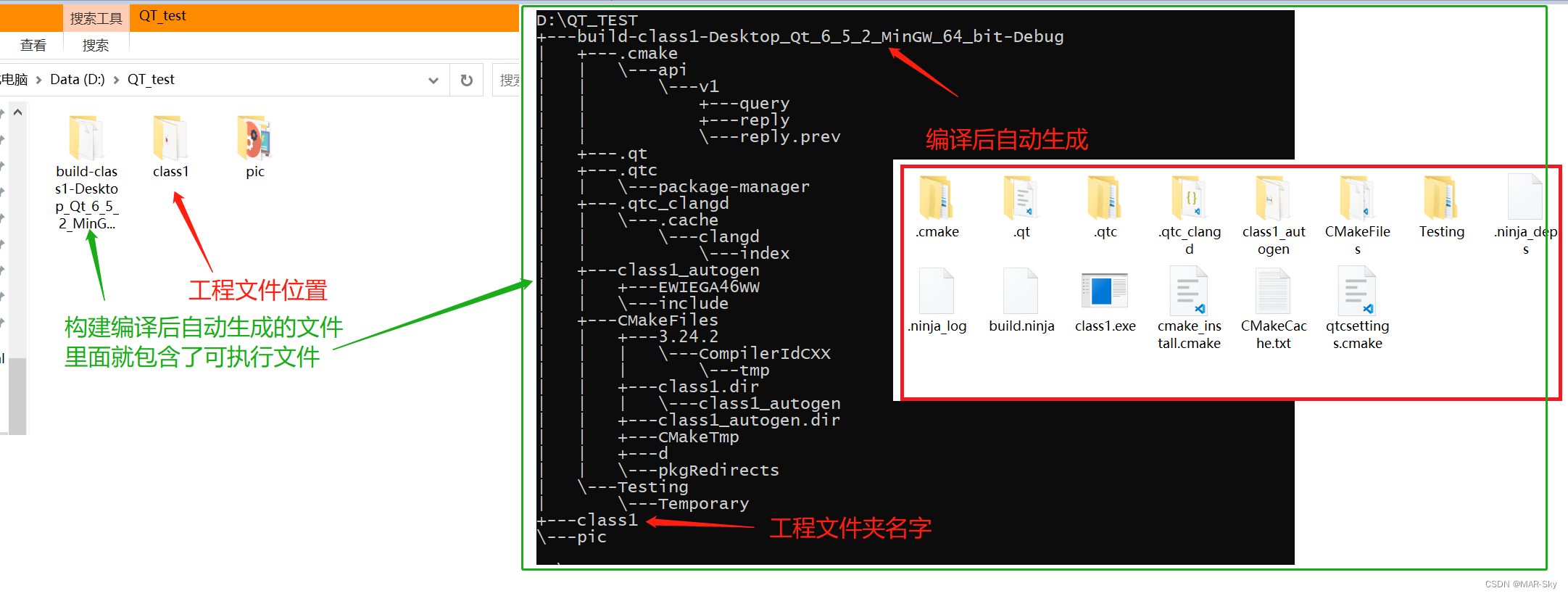
QT6编译的文件分布情况
工程文件和编译文件位置分布 工程文件是自己建立的源文件位置,而同等级的位置在工程构建时会重新生成一个编译后的文件夹,里面包含了可执行的exe文件。而这个文件夹的内容也是QT ide运行时读取的文件,但这个文件的内容在IDE中如果不重新构建…...

2023中国算力大会 | 中科驭数加入DPU推进计划,探讨DPU如何激活算网融合新基建
8月18日,由工业和信息化部、宁夏回族自治区人民政府共同主办的2023中国算力大会在宁夏银川隆重召开。作为DPU算力基础设施领军企业,中科驭数产品运营部副总经理曹辉受邀在中国信通院承办的算网融合分论坛发表主题演讲《释放极致算力 DPU激活算网融合新基…...
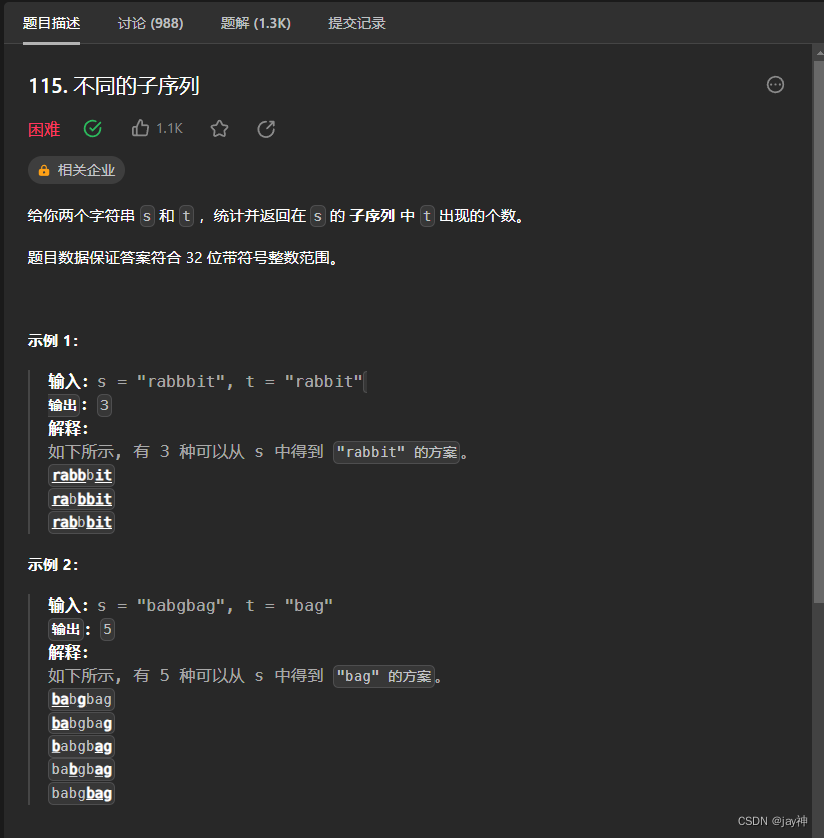
leetcode 115. 不同的子序列
2023.8.25 使用dp数组解决。 定义一个二维dp数组,dp[i][j]的含义为:字符串s(下标为i-1)中,子序列t(下标为j-1)出现的个数。 当字符串s[i-1]和t[j-1]相同时,递推公式为:d…...

gradio应用transformer模块部署生成式人工智能应用程序
文章目录 gradio简介hello world范例文本分类文本问答抽取式问答gr.Interface自定义实现问答Blocks使用gradio简介 gradio只需在原有的代码中增加几行,就能自动化生成交互式web页面,并支持多种输入输出格式,比如图像分类中的图>>标签,超分辨率中的图>>图等。 …...
【目标检测】“复制-粘贴 copy-paste” 数据增强实现
文章目录 前言1. 效果展示代码说明3. 参考文档4. 不合适点 前言 本文来源论文《Simple Copy-Paste is a Strong Data Augmentation Method for Instance Segmentation》(CVPR2020),对其数据增强方式进行实现。 论文地址:https:/…...

深度学习知识总结2:主要涉及深度学习基础知识、卷积神经网络和循环神经网络
往期链接:Summer 1 : Summarize linear neural networks and multi-layer perceptron Summer 2: Summarize CNN and RNN 文章目录 Summer 2: Summarize CNN and RNNPart 1 Deep Learning> 层和块> 参数管理和延后初始化> 读写文件和GPU Part 2 CNN> 从…...
Spring Boot 集成 WebSocket 实现服务端推送消息到客户端
WebSocket 简介 WebSocket 协议是基于 TCP 的一种新的网络协议,它实现了浏览器与服务器全双工(full-duplex)通信—允许服务器主动发送信息给客户端,这样就可以实现从客户端发送消息到服务器,而服务器又可以转发消息到客…...

vr游乐场项目投资方案VR主题游乐馆互动体验
VR文旅景区沉浸互动体验项目是指利用虚拟现实技术在文旅景区中创建沉浸式的互动体验项目。通过虚拟现实技术,游客可以身临其境地体验景区的风景和文化,与虚拟场景中的元素进行互动。 普乐蛙VR设备 普乐蛙VR设备案例分享 这种项目可以为游客带来全新的旅游…...
)
chrom扩展开发配合百度图像文字识别实现自动登录(后端.net core web api)
好久没做浏览器插件开发了,因为公司堡垒机,每次登录都要输入账号密码和验证码。太浪费时间了,就想着做一个右键菜单形式的扩展。 实现思路也很简单,在这里做下记录,方便下次开发参考。 一,先来了解下chro…...

香港服务器怎么打开SSH
SSH是一种远程登录协议,可以通过加密方式在网络上安全地传输数据。它允许用户在远程服务器上执行命令,管理文件和目录,并进行其他系统管理任务。 如何打开SSH服务? 1.确认已安装OpenSSH服务器: 你可以通过命令sudoapt-geti…...
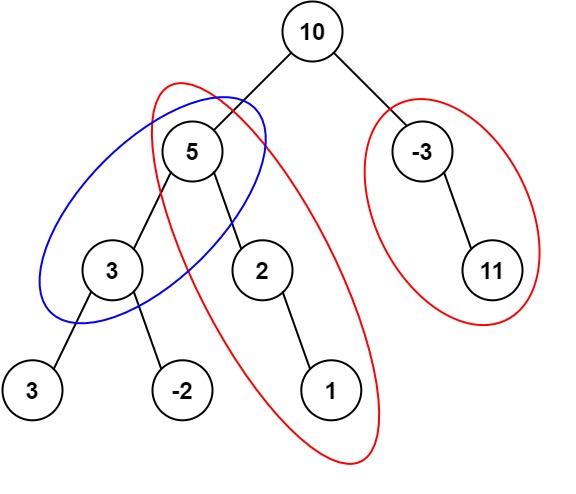
【LeetCode】437.路径总和Ⅲ
题目 给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。 路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节…...

Mybatis-plus中操作JSON字段
1.实体类上要加上自动映射 TableName(value "school", autoResultMap true)2.json字段上加上json处理器 TableField(value "cover_url", typeHandler JacksonTypeHandler.class)private List<String> cover_url;参考博客 http://www.dedeyun.co…...
第十五课、Windows 下打包发布 Qt 应用程序
功能描述:讲解了 Windows 下打包发布 Qt 应用程序的三种方法,并对比优缺点 一、利用 windepolyqt 工具打包发布 Qt 提供了一个 windeployqt 工具来自动创建可部署的文件夹。 打包发布流程: 1. 新建一个文件夹,将编译后的可执行…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...
——Oracle for Linux物理DG环境搭建(2))
Oracle实用参考(13)——Oracle for Linux物理DG环境搭建(2)
13.2. Oracle for Linux物理DG环境搭建 Oracle 数据库的DataGuard技术方案,业界也称为DG,其在数据库高可用、容灾及负载分离等方面,都有着非常广泛的应用,对此,前面相关章节已做过较为详尽的讲解,此处不再赘述。 需要说明的是, DG方案又分为物理DG和逻辑DG,两者的搭建…...
