高精度运算(加减乘除乘法)
所谓高精度,就是大数的运算,这个大数可能是要远远超过现有数据类型的最大范围。如果我们想进行这样的运算,就要掌握计算的原理——竖式运算。`
加法
我们这里先简单考虑非负数的加法,竖式这么列对吧:
①存储
我们如何储存过长的数呢?可以用数组存储。怎么才能将各个数位上的数放到数组里面呢?这里,我们可以使用字符串。
我们使用逆序储存,这样会比较方便,后面可以在result数组中反向输出。
int a[241]=,b[241],result[242],l1=0,l2=0;
string c,d;
cin>>c>>d;
// 第一步读取整数
for(int i=c.size()-1;i>=0;i--){a[l1++]=c[i]-'0';
}
for(int i=d.size()-1;i>=0;i--){b[l2++]=d[i]-'0';
}
同时,这里l1表示第一个加数的长度,l2表示第二个加数的长度。
②模拟加法运算
接着,模拟运算:
// 第二步加法计算int l=max(l1,l2)for(int i=0;i<l;i++){result[i]+=(a[i]+b[i])%10;result[i+1]+=(a[i]+b[i])/10;}
当我们进行加法运算时,每一位的结果是由两个部分组成的:当前位的数字和从低位“进”来的数字。例如,当我们计算23 + 18时,个位的结果是1,这个1就是从低位“进”来的,而2和3相加的结果是5,这个5就是当前位的数字。
在计算机中,当我们进行高精度计算时,通常会把每个数字拆分成多个位(如一个8位数字可以拆分成个位、十位、百位等),然后逐位进行加法运算。为了得到每个位的正确结果,我们需要考虑从低位“进”来的数字。
例如,如果我们有两个8位数字1234和5678,我们不能直接把它们相加,因为结果会超过8位。正确的做法是逐位进行加法运算:
1 + 6 = 7,没有进位,所以结果的个位就是7
2 + 7 = 9,进位1,所以结果的十位就是9 + 1 = 09
3 + 8 = 11,进位1,所以百位的结果是11 + 1 = 01
4 + 5 = 9,进位1,所以千位的结果是09 + 1 = 009
这样,我们就可以得到最终的结果:0097。
在上面的程序中,“进位”的思想体现在每次加法运算时都考虑了前一位的进位。通过这种方式,我们可以得到正确的高精度结果。
③反向输出:
for(int i=(x>y?x:y);i>=0;i--){cout<<result[i];
}
完整代码:
#include <iostream>
using namespace std;
int main(){// 高精度加法 240位内,调整数组大小可以扩大位数 int a[241]={},b[241]={},result[242]={},l1=0,l2=0;string c,d;cin>>c>>d;// 第一步读取整数for(int i=c.size()-1;i>=0;i--){a[l1++]=c[i]-'0';}for(int i=d.size()-1;i>=0;i--){b[l2++]=d[i]-'0';}int l=max(l1,l2); // 第二步加法计算for(int i=0;i<l;i++){result[i]+=(a[i]+b[i])%10;result[i+1]+=(a[i]+b[i])/10;}for(int i=l;i>=0;i--){cout<<result[i];}return 0;
}
减法
不说什么了,与上同理
#include <iostream>
using namespace std;
int main(){string s1,s2;int a[241]={},b[241]={},result[241]={},k=0,t;cin>>s1>>s2;// 考虑几种特殊情况if(s1==s2){cout<<0;return 0;}if(s1.size()<s2.size()||s1.size()==s2.size()&&s1<s2){cout<<"-";swap(s1,s2);}// 存储数据for(int i=0;i<s1.size();i++){a[s1.size()-i-1]=s1[i]-'0';}for(int i=0;i<s2.size();i++){b[s2.size()-i-1]=s2[i]-'0';}// 模拟竖式的算法for(int i=0;i<(s1.size()>s2.size()?s1.size():s2.size());i++){t=10-b[i]+a[i]+result[k++];if(t<10) result[k]--; // 退位,在后面一位减去1result[k-1]=t%10;}// 前面可能有0,从第一个不是0的数开始输出for(int i=k-1;i>=0;i--){if(result[i]>0){t=i; // 记录第一个不是0的数break;}}// 输出for(int i=t;i>=0;i--){cout<<result[i];}return 0;
}
放到草稿纸上,想想就明白了。
乘法
高精度乘单精度
我们用单精度去乘高精度的每一位,然后累加。
#include <iostream>
using namespace std;
int main(){// 高精度乘单精度(不超过10000)int a[251]={};string s1;int b;cin>>s1>>b;for(int i=0;i<s1.size();i++){a[i]=s1[s1.size()-i-1]-'0';}// 按位相乘for(int i=0;i<s1.size();i++){a[i]=a[i]*b;}// 处理进位for(int i=0;i<s1.size()+4;i++){if(a[i]>=10){a[i+1]+=a[i]/10;a[i]%=10;}}// 获取第一个不是0的数int point=0;for(int i=s1.size()+4;i>=0;i--){if(a[i]!=0){point=i;break;}}for(int i=point;i>=0;i--){cout<<a[i];}return 0;
}
高精度乘高精度
最难的地方,需要找找规律!
#include <iostream>
using namespace std;
int main(){// 高精度乘高精度string s1,s2;int a[251],b[251],c[503]={};cin>>s1>>s2;for(int i=0;i<s1.size();i++) a[i]=s1[s1.size()-i-1]-'0';for(int i=0;i<s2.size();i++) b[i]=s2[s2.size()-i-1]-'0';for(int i=0;i<s1.size();i++){for(int j=0;j<s2.size();j++){// ↓ 这里是 +=c[i+j]+=a[i]*b[j];// 进位if(c[i+j]>=10){c[i+j+1]+=c[i+j]/10;c[i+j]%=10;}}}int p=0;// 找到不是0的数for(int i=s1.size()+s2.size()-1;i>=0;i--){if(c[i]!=0){p=i;break;}}// 从p开始输出for(int i=p;i>=0;i--){cout<<c[i];}return 0;
}
除法
#include <iostream>
using namespace std;
int main(){int a,b,n,t=0,c[1001];cin>>a>>b>>n;cout<<a/b<<".";a=(a%b)*10;for(int i=0;i<n;i++){c[t++]=a/b;a=(a%b)*10;}for(int i=0;i<t;i++){cout<<c[i];}return 0;
}这个程序首先接收三个输入:两个整数a和b以及一个整数n,它们分别代表被除数、除数和小数的位数。
然后程序计算出a除以b的商并输出,然后保留这个商的余数。这个余数就是小数点后的第一位。
接着,程序进入一个for循环,该循环执行n次。在每次循环中,它将余数除以b(实际上是一个乘以10的操作),得到下一位小数,然后将这个值存储在数组c中。然后再次保留这个新得到的余数。
最后,程序再输出数组c中的所有值,这些值就是小数a/b的前n位小数。
这个程序使用了小学奥数中的知识:如果你要得到一个数的n位小数,你可以不断地对余数乘以10,然后除以除数,直到得到n位小数为止。
乘方(2的n次方)
思路是高精度乘单精度,单精度的永远是2,然后循环。
#include <iostream>
using namespace std;
int main(){/*高精度2的乘方思路:高精度*单精度2,循环n次*/int a[251]={1},n,len=1;cin>>n;for(int i=1;i<=n;i++){// 按位相乘for(int j=0;j<len;j++){a[j]*=2;}// 处理进位for(int j=0;j<len;j++){if(a[j]>=10){a[j+1]+=a[j]/10;a[j]%=10;}}if(a[len]>0) len++;}for(int i=len-1;i>=0;i--){cout<<a[i];}return 0;
}1.创建一个长度为251的数组a,并将第一个元素初始化为1。这个数组用来存储每一位的数字。
2.读入一个整数n,表示要计算2的n次方。
3.使用一个外层循环,从1到n进行迭代。在每次循环中,执行以下步骤:
1)使用一个内层循环,从0到len-1进行迭代。这个循环的作用是将数组a中的每一位乘以2。
2)再使用一个内层循环,从0到len-1进行迭代。这个循环的作用是处理进位。如果当前位乘以2之后超过了10,就需要向下一个位置进位。具体做法是,将当前位置除以10的结果加到下一个位置上,然后将当前位置取模10,得到新的当前位置的值。
3)如果处理完所有位置之后,最高位(位置len)的值仍然大于0,就将len加1,表示数组a的长度还需要增加一位。
4.最后,使用一个倒序循环,从len-1到0进行迭代。这个循环的作用是将数组a中的每一位输出到屏幕上。
相关文章:
)
高精度运算(加减乘除乘法)
所谓高精度,就是大数的运算,这个大数可能是要远远超过现有数据类型的最大范围。如果我们想进行这样的运算,就要掌握计算的原理——竖式运算。 加法 我们这里先简单考虑非负数的加法,竖式这么列对吧: ①存储 我们如何…...

Mysql数据库技术知识整理
Mysql的知识点目录 重点:架构,引擎,索引,锁机制,事务机制,日志机制,集群,调优 3、Mysql索引 索引概念 覆盖索引: 条件列和结果列都在索引中索引下推: 查询会先过滤条件列,然后回表查数据最左前缀匹配&am…...
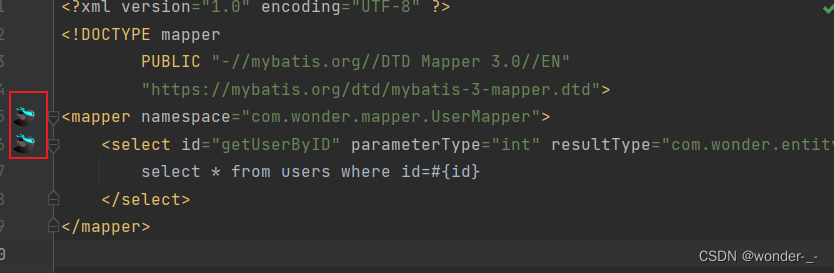
SpringBoot整合Mybatis 简单试用
1. 导入依赖 我使用MySQL,需要导入MySQL的驱动依赖此外要在SpringBoot中使用Mybatis,则需要导入Mybatis启动器 <dependency><groupId>org.mybatis.spring.boot</groupId><artifactId>mybatis-spring-boot-starter</artifact…...
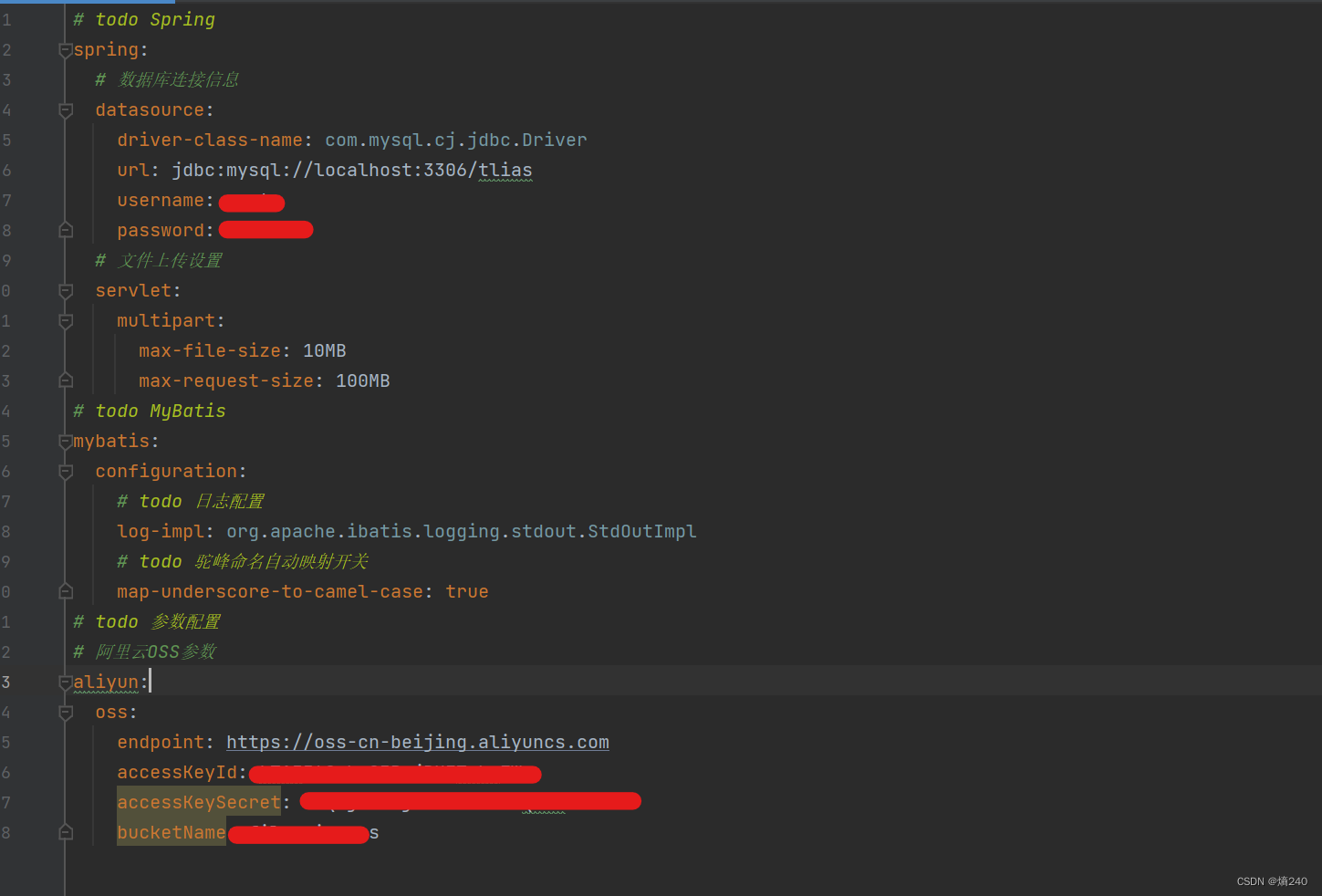
SpringBoot案例-配置文件-yml配置文件
配置格式 SpringBoot提供了多种属性配置方式 application.propertiesapplication.ymlapplication.yaml常见配置文件格式对比 XML(臃肿) <configuration><database><host>localhost</host><port>3306</port><use…...

Web Components
Web Components标准非常重要的一个特性是,它使开发者能够将HTML页面的功能封装为custom elements(自定义标签),可以使用CustomElementRegistry来管理自定义标签 <script>//1、创建自定义标签class NewElement extends HTML…...

IT运维软件的费用是多少?
正常一套IT运维软件费用一般在5千-50万之间不等,而且分为一次性付费或年付费模式,付费方式导致的价格也不同。 正常情况下IT运维软件的具体价格,是需要根据企业的实际需求来进行综合评估,一般来说,影响具体价格费用有以…...
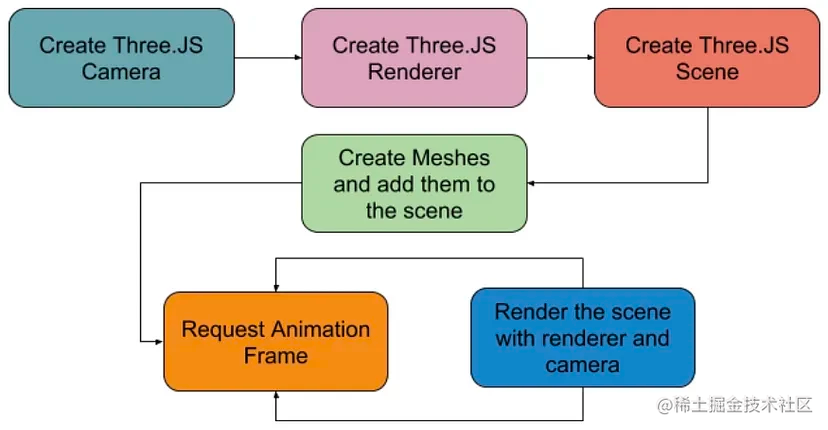
基于Three.js的WebXR渲染入门
1、Three.js 渲染管线快速概览 我不会花太多时间讨论 Three.JS 渲染管道的工作原理,因为它在互联网上有详细记录(例如,此链接)。 我将在下图中列出基础知识,以便更容易理解各个部分的去向。 2、WebXR 设备 API 入门 在我们深入了解 WebXR API 本身之前,您应该知道 WebX…...
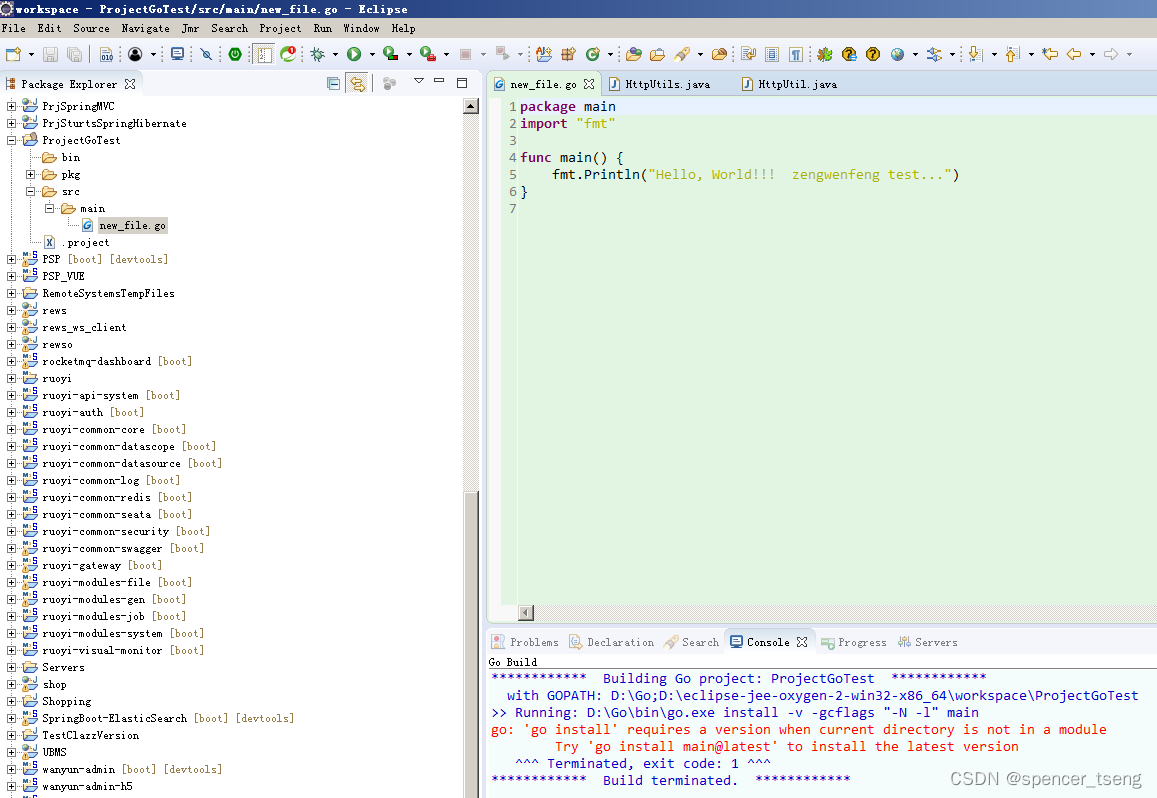
resource doesn‘t have a corresponding Go package.
resource doesnt have a corresponding Go package. GO这个鬼东西不能直接放src下。 ************ Building Go project: ProjectGoTest ************with GOPATH: D:\Go;D:\eclipse-jee-oxygen-2-win32-x86_64\workspace\ProjectGoTest >> Running: D:\Go\bin\go.exe …...
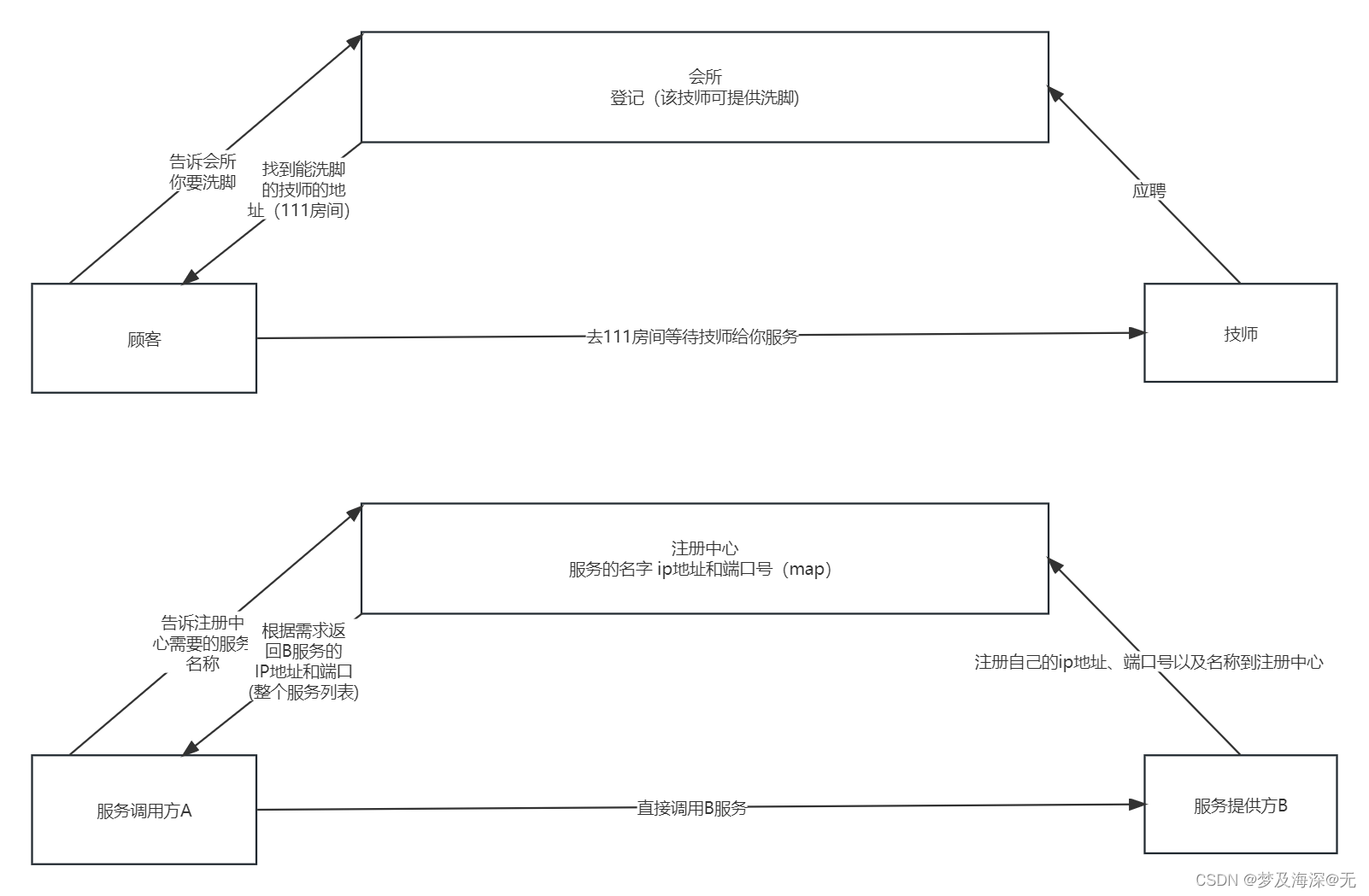
【微服务】微服务调用原理及服务治理
本文通过图文结合,简要讲述微服务的调用原理,以及服务治理的相关概念。 1.微服务的调用原理 举个栗子:你去会所洗脚。首先,技师肯定要先去会所应聘,通过之后,会所会记录该技师的信息和技能,然后…...

【在Windows下搭建Tomcat HTTP服务】
文章目录 前言1.本地Tomcat网页搭建1.1 Tomcat安装1.2 配置环境变量1.3 环境配置1.4 Tomcat运行测试1.5 Cpolar安装和注册 2.本地网页发布2.1.Cpolar云端设置2.2 Cpolar本地设置 3.公网访问测试4.结语 前言 Tomcat作为一个轻量级的服务器,不仅名字很有趣࿰…...

前端Vue3框架知识点大全
Vue.js是一种流行的JavaScript前端框架,它的第三个版本Vue3带来了许多令人兴奋的新特性和改进。 1、响应式数据: Vue 3采用了基于Proxy的响应式系统,相比Vue 2中的Object.defineProperty,Proxy提供了更强大和灵活的拦截器&#…...

C语言练习2(巩固提升)
C语言练习2 选择题 前言 “志之所趋,无远弗届,穷山距海,不能限也。”对想做爱做的事要敢试敢为,努力从无到有、从小到大,把理想变为现实。要敢于做先锋,而不做过客、当看客,让创新成为青春远航的…...

Vulnhub: DriftingBlues: 1靶机
kali:192.168.111.111 靶机:192.168.111.215 信息收集 端口扫描 nmap -A -sC -v -sV -T5 -p- --scripthttp-enum 192.168.111.215 80端口首页源码 访问noteforkingfish.txt,发现为Ook!加密的密文 解密后提示需要用户eric和修改hosts文件&…...
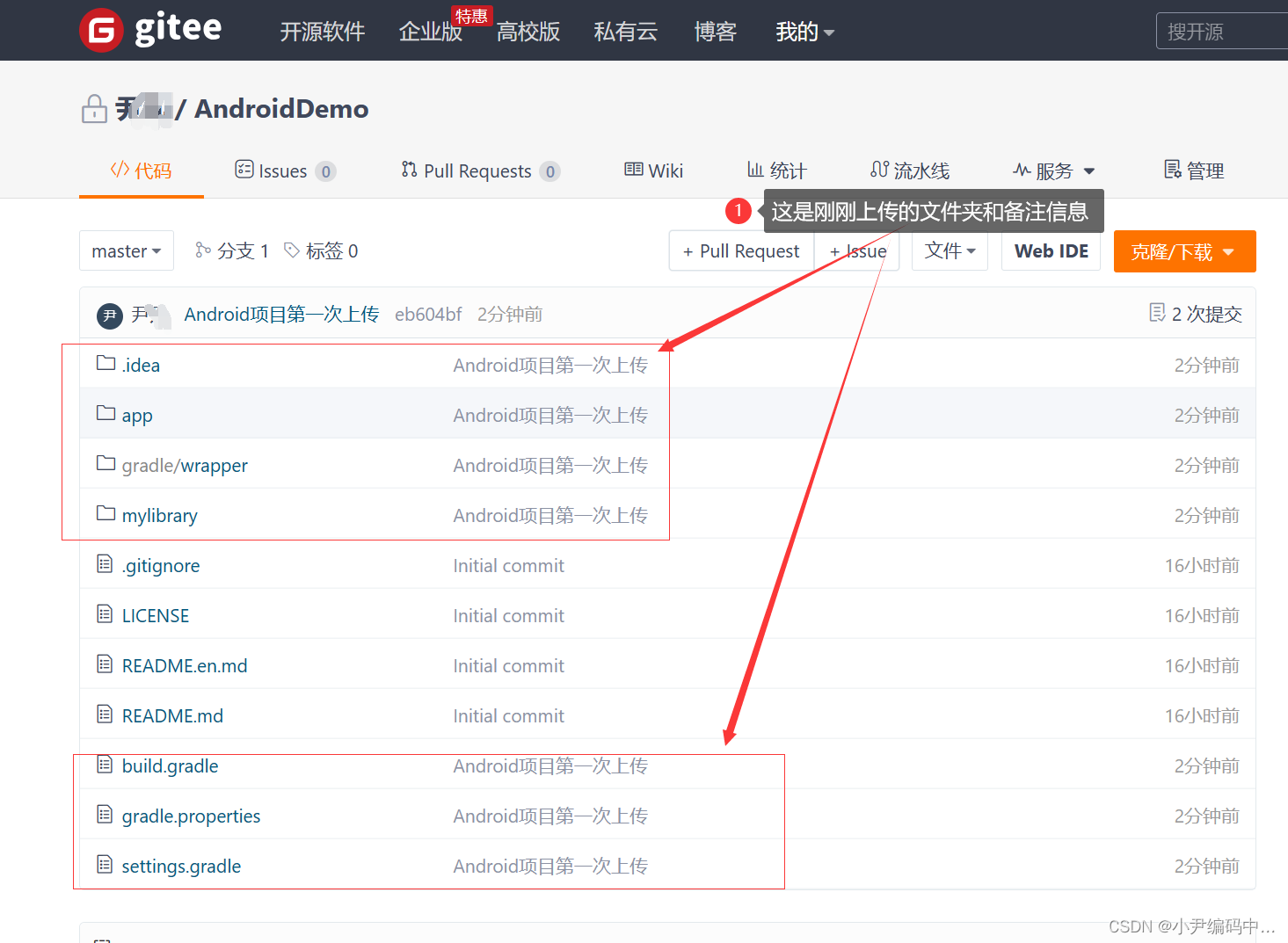
Android项目如何上传Gitee仓库
前言 最近Android项目比较多,我都是把Android项目上传到Gitee中去,GitHub的话我用的少,可能我还是更喜欢Gitee吧,毕竟Gitee仓库用起来更加方便 一. 创建Gitee仓库 1. 先创建一个Gitee账号,然后登录上去 2. 创建Androi…...

MySQL——基础——联合查询
联合查询 - union,union all 对于union查询,就是把多次查询的结果合并起来,形成一个新的查询结果集 SELECT 字段列表 FROM 表A ... UNION [ALL] SELECT 字段列表 FROM 表B ...; 1.将薪资低于5000的员工,和 年龄大于50的员工全部查询出来 use itcast; select * from participat…...

Vue3+Vite 初始化Cesium
Vue3Vite 初始化Cesium 安装依赖 yarn add cesium yarn add vite-plugin-cesium -D加载vite-plugin-cesium插件 import { defineConfig } from vite import vue from vitejs/plugin-vue import cesium from vite-plugin-cesium;export default defineConfig({plugins: [vue(…...
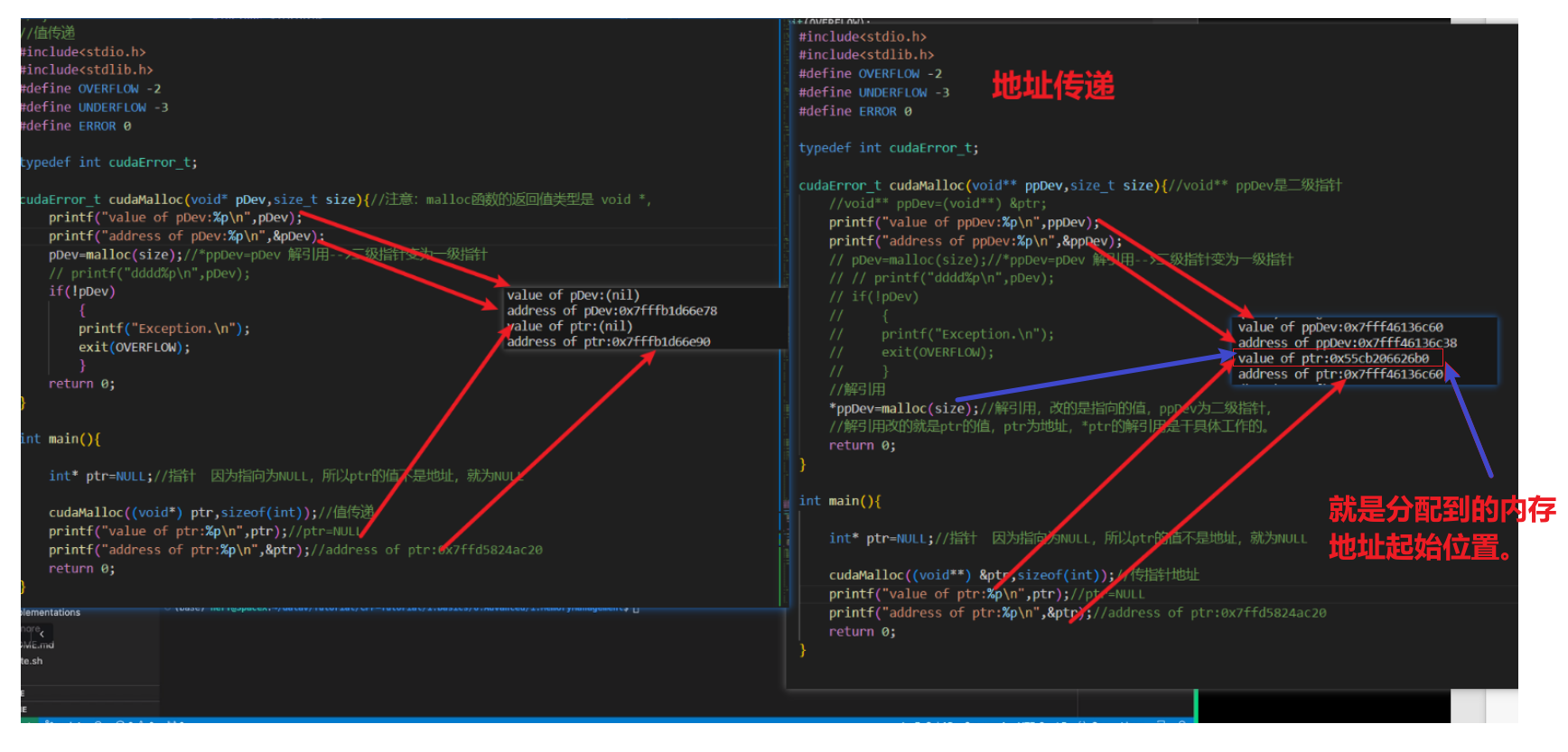
c++内存地址分配
...
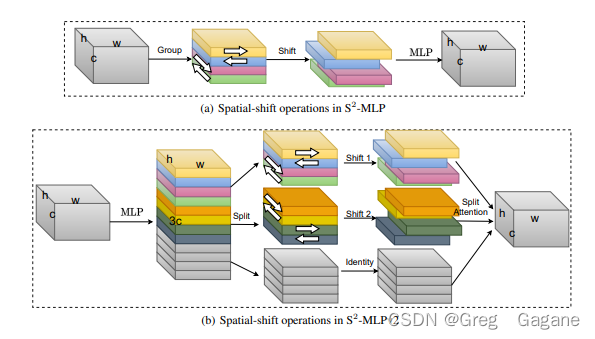
改进YOLO系列:9.添加S2Attention注意力机制
添加S2Attention注意力机制 1. S2Attention注意力机制论文2. S2Attention注意力机制原理3. S2Attention注意力机制的配置3.1common.py配置3.2yolo.py配置3.3yaml文件配置1. S2Attention注意力机制论文 论文题目:S 2 -MLPV2: IMPROVED SPATIAL-SHIFT MLP ARCHITECTURE…...

微服务Feign组件远程调用自定义解码器
Feign远程调用响应结果格式 public class Result<T> {/*** 响应码,200为成功*/private Integer code;/*** 响应信息*/private String message;/*** 响应的具体对象*/private T data; }自定义Feign解码器 Component // 注入Spring的IOC容器中,所有…...
FairyGUI编辑器自定义菜单扩展插件
本文涉及到的软件有:FairyGUI,VSCode 代码环境涉及到了:Lua VSCode插件:EmmyLua 在编写FairyGUI编辑器菜单前,了解一下FairyGUIEditor的API会有效的帮助我们解决很多问题。FairyGUI的扩展是通过编辑器自带的插件功能…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
