Layer Normalization(层规范化)
详细内容在这篇论文:Layer Normalization
训练深度神经网络需要大量的计算,减少计算时间的一个有效方法是规范化神经元的活动,例如批量规范化BN(batch normalization)技术,然而,批量规范化对小批量大小(batch size)敏感并且无法直接应用到RNN中(recurrent neural networks),为了解决上述问题,层规范化LN(Layer Normalization)被提出,不仅能直接应用到RNN,还能显著减少训练时间。与批量归一化不同,层规范化直接根据隐藏层内神经元的总输入估计归一化统计数据,因此不会在训练案例之间引入任何新的依赖关系。
背景
A feed-forward neural network is a non-linear mapping from a input pattern x \mathbf{x} x to an output vector y y y. Consider the l th l^{\text {th }} lth hidden layer in a deep feed-forward, neural network, and let a l a^l al be the vector representation of the summed inputs to the neurons in that layer. a i l a_i^l ail是第 l l l层第 i i i个神经元的线性加权输出。 The summed inputs are computed through a linear projection with the weight matrix W l W^l Wl and the bottom-up inputs h l h^l hl given as follows:
a i l = w i l ⊤ h l h i l + 1 = f ( a i l + b i l ) a_i^l=w_i^{l^{\top}} h^l \quad h_i^{l+1}=f\left(a_i^l+b_i^l\right) ail=wil⊤hlhil+1=f(ail+bil)
where f ( ⋅ ) f(\cdot) f(⋅) is an element-wise non-linear function(激活函数) and w i l w_i^l wil is the incoming weights to the i t h i^{t h} ith hidden units and b i l b_i^l bil is the scalar bias parameter. The parameters in the neural network are learnt using gradient-based optimization algorithms with the gradients being computed by back-propagation.
Batch Normalization
BN是为了减少协变量偏移提出的,它在训练阶段对隐神经元加权输出进行规范化,例如,对于 l t h l^{th} lth层的 i t h i^{th} ith个加权输出 a i l a_i^l ail,BN根据输入数据的分布进行了缩放
a ˉ i l = g i l σ i l ( a i l − μ i l ) μ i l = E x ∼ P ( x ) [ a i l ] σ i l = E x ∼ P ( x ) [ ( a i l − μ i l ) 2 ] \bar{a}_i^l=\frac{g_i^l}{\sigma_i^l}\left(a_i^l-\mu_i^l\right) \quad \mu_i^l=\underset{\mathbf{x} \sim P(\mathbf{x})}{\mathbb{E}}\left[a_i^l\right] \quad \sigma_i^l=\sqrt{\underset{\mathbf{x} \sim P(\mathbf{x})}{\mathbb{E}}\left[\left(a_i^l-\mu_i^l\right)^2\right]} aˉil=σilgil(ail−μil)μil=x∼P(x)E[ail]σil=x∼P(x)E[(ail−μil)2]
where a ˉ i l \bar{a}_i^l aˉil is normalized summed inputs to the i t h i^{t h} ith hidden unit in the l t h l^{t h} lth layer and g i g_i gi is a gain parameter scaling the normalized activation before the non-linear activation function.
实际中不会计算真正的 μ \mu μ和 σ \sigma σ,转而去估计一个batch里的 μ \mu μ和 σ \sigma σ,所以BN要求这个batchsize不能太小。然而,在一些在线学习任务以及超大分布模型中往往需要很小的batchsize。
Layer Normalization
μ l = 1 H ∑ i = 1 H a i l σ l = 1 H ∑ i = 1 H ( a i l − μ l ) 2 \mu^l=\frac{1}{H} \sum_{i=1}^H a_i^l \quad \sigma^l=\sqrt{\frac{1}{H} \sum_{i=1}^H\left(a_i^l-\mu^l\right)^2} μl=H1i=1∑Hailσl=H1i=1∑H(ail−μl)2
H H H是一个隐藏层中的隐藏单元数量。在LN中,同一个层共享 μ \mu μ和 σ \sigma σ, but different training cases have different normalization terms. Unlike batch normalization, layer normalization does not impose any constraint on the size of a mini-batch and it can be used in the pure online regime with batch size 1.
In a standard RNN, the summed inputs in the recurrent layer are computed from the current input x t \mathbf{x}^t xt and previous vector of hidden states h t − 1 \mathbf{h}^{t-1} ht−1 which are computed as a t = W h h h t − 1 + W x h x t \mathbf{a}^t=W_{h h} h^{t-1}+W_{x h} \mathbf{x}^t at=Whhht−1+Wxhxt. The layer normalized recurrent layer re-centers and re-scales its activations using the extra normalization terms :
h t = f [ g σ t ⊙ ( a t − μ t ) + b ] μ t = 1 H ∑ i = 1 H a i t σ t = 1 H ∑ i = 1 H ( a i t − μ t ) 2 \mathbf{h}^t=f\left[\frac{\mathbf{g}}{\sigma^t} \odot\left(\mathbf{a}^t-\mu^t\right)+\mathbf{b}\right] \quad \mu^t=\frac{1}{H} \sum_{i=1}^H a_i^t \quad \sigma^t=\sqrt{\frac{1}{H} \sum_{i=1}^H\left(a_i^t-\mu^t\right)^2} ht=f[σtg⊙(at−μt)+b]μt=H1i=1∑Haitσt=H1i=1∑H(ait−μt)2
where W h h W_{h h} Whh is the recurrent hidden to hidden weights and W x h W_{x h} Wxh are the bottom up input to hidden weights. ⊙ \odot ⊙ is the element-wise multiplication between two vectors. b \mathbf{b} b and g \mathbf{g} g are defined as the bias and gain parameters of the same dimension as h t \mathbf{h}^t ht.
在标准RNN中存在梯度爆炸和消失问题,用了LN之后会更加稳定。
贴两个图便于理解:

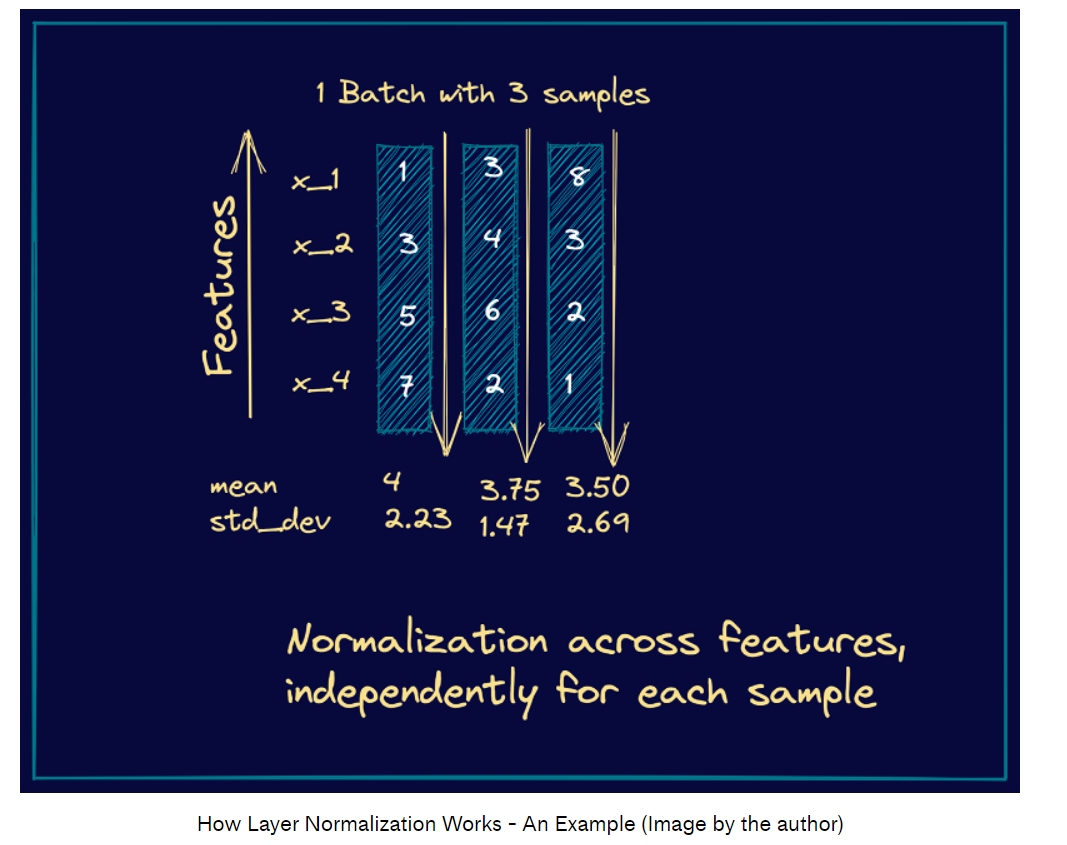
视频讲解可以参考:What is Layer Normalization? | Deep Learning Fundamentals
代码实现
这边贴一个Restormer中的LN层的实现
首先定义两个函数用于reshape。4d到3d不需要参数,因为只需要把已有的两个维度合并;3d到4d需要参数,因为需要把一个维度分成两个维度
def to_3d(x):return rearrange(x, 'b c h w -> b (h w) c')def to_4d(x,h,w):return rearrange(x, 'b (h w) c -> b c h w',h=h,w=w)
定义一个没有bias的LN层,weight是可学习的参数,所以用 n n . P a r a m e t e r nn.Parameter nn.Parameter包装
# 没有bias的LayerNorm层
class BiasFree_LayerNorm(nn.Module):def __init__(self, normalized_shape):super(BiasFree_LayerNorm, self).__init__()if isinstance(normalized_shape, numbers.Integral):normalized_shape = (normalized_shape,)normalized_shape = torch.Size(normalized_shape)assert len(normalized_shape) == 1self.weight = nn.Parameter(torch.ones(normalized_shape))self.normalized_shape = normalized_shapedef forward(self, x):#x的维度(batch_size, height x width, channels)#sigma的维度(batch_size, height x width, 1)sigma = x.var(-1, keepdim=True, unbiased=False)return x / torch.sqrt(sigma+1e-5) * self.weight
定义一个有bias的LN层,同样的,weight和bias都是可学习的参数
class WithBias_LayerNorm(nn.Module):def __init__(self, normalized_shape):super(WithBias_LayerNorm, self).__init__()#如果输入的normalized_shape是个整数,则化为元组if isinstance(normalized_shape, numbers.Integral):normalized_shape = (normalized_shape,)normalized_shape = torch.Size(normalized_shape)assert len(normalized_shape) == 1self.weight = nn.Parameter(torch.ones(normalized_shape))#比上面多定义一个biasself.bias = nn.Parameter(torch.zeros(normalized_shape))self.normalized_shape = normalized_shapedef forward(self, x):mu = x.mean(-1, keepdim=True)sigma = x.var(-1, keepdim=True, unbiased=False)return (x - mu) / torch.sqrt(sigma+1e-5) * self.weight + self.bias#这边加了bias把上面的函数包装起来,定义一个统一的层规范化函数
class LayerNorm(nn.Module):def __init__(self, dim, LayerNorm_type):super(LayerNorm, self).__init__()if LayerNorm_type =='BiasFree':self.body = BiasFree_LayerNorm(dim)else:self.body = WithBias_LayerNorm(dim)def forward(self, x):h, w = x.shape[-2:]return to_4d(self.body(to_3d(x)), h, w)
相关文章:

Layer Normalization(层规范化)
详细内容在这篇论文:Layer Normalization 训练深度神经网络需要大量的计算,减少计算时间的一个有效方法是规范化神经元的活动,例如批量规范化BN(batch normalization)技术,然而,批量规范化对小批…...

redisson参数配置
文章目录 pom配置链接配置建议 pom <!-- 引入spring-data-redis组件 --> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId><exclusions><!-- 因springboot2.x…...

【基于Arduino的仿生蚂蚁机器人】
【基于Arduino的仿生蚂蚁机器人】 1. 概述2. Arduino六足位移台–蚂蚁机器人3D模型3. 3D 打印零件4. 组装Arduino六足位移台5. Arduino蚂蚁机器人电路图6. 为Arduino Hexapod设计PCB7. 组装电路板8. 系统代码9. Arduino蚂蚁机器人安卓应用程序在本教程中,我将向您展示如何构建…...

angular12里面FormGroup做多个项目的相关check
FromFroup在鼠标失去焦点时做相关check,可以在group方法第二个参数的位置加一个对象参数 { validator: this.checkPasswords } 在Angular 12中,可以使用formGroup来进行两个密码是否一致的检查。以下是一个示例: 首先,在组件的…...

TypeScript 的发展与基本语法
目录 一、为什么什么是TypeScript? 1、发展历史 2、typescript与javascript 3、静态类型的好处 二、基础语法 1、基础数据类型 2、补充类型 3、泛型 4、泛型的高级语法 5、类型别名&类型断言 6、字符串/数字 字面量 三、高级类型 1、联合/交叉类型…...
)
macOS - 上编译运行 risc-v (spike)
文章目录 一、说明二、安装步骤三、测试 一、说明 本文根据以下文章改编: RISC-V 环境配置 https://decaf-lang.github.io/minidecaf-tutorial/docs/step0/riscv_env.html 相关链接: riscv-gnu-toolchain GNU toolchain for RISC-V, including GCC ht…...
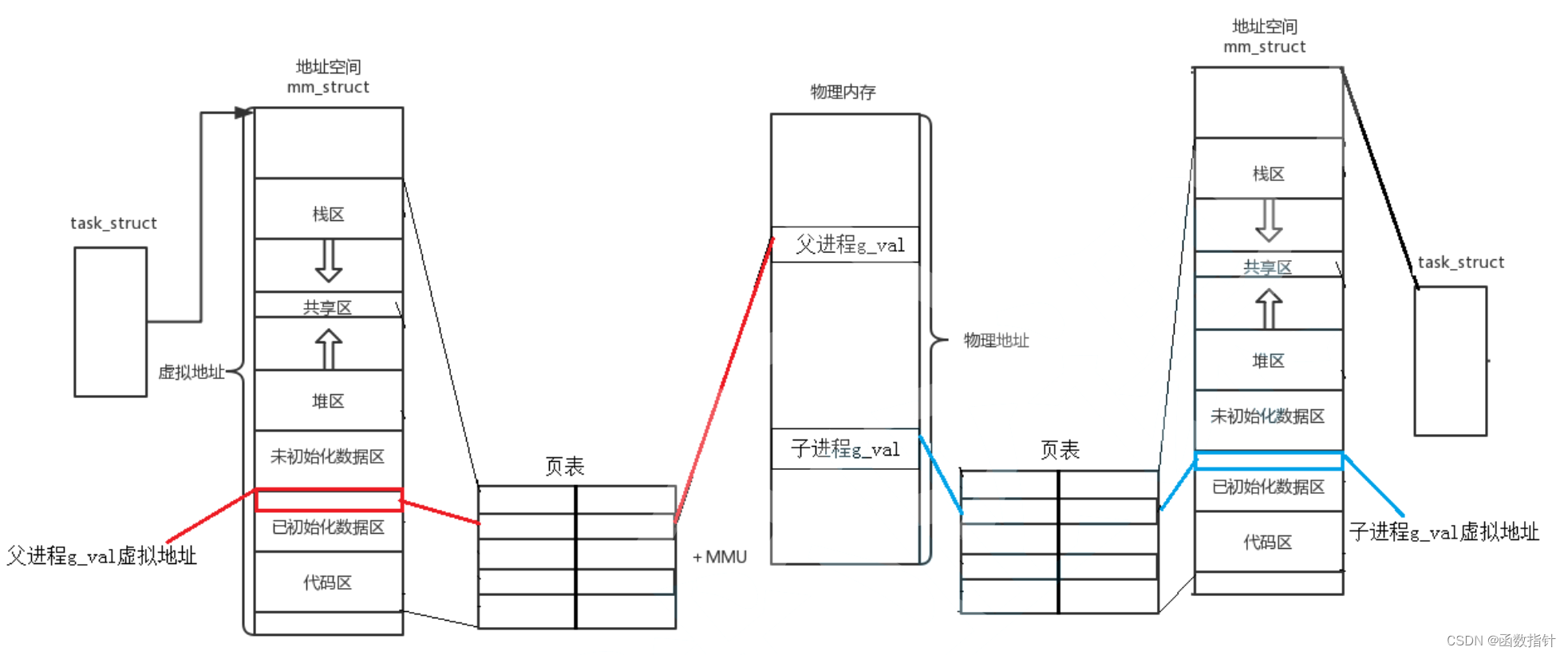
Linux--线程地址空间
1.程序地址空间 先来就看这张图 这是一张程序地址分布的图,通过一段代码来证明地址空间的分布情况 编译结果: 可以看出的是,父子进程中对于同一个变量打印的地址是一样的,这是因为子进程以父进程为模板,因为都没有对数…...

华为OD机试 - 最佳植树距离 - 二分查找(Java 2023 B卷 100分)
目录 一、题目描述二、输入描述三、输出描述四、备注说明五、二分查找六、解题思路七、Java算法源码八、效果展示1、输入2、输出3、说明 一、题目描述 按照环保公司要求,小明需要在沙化严重的地区进行植树防沙工作,初步目标是种植一条直线的树带。 由于…...
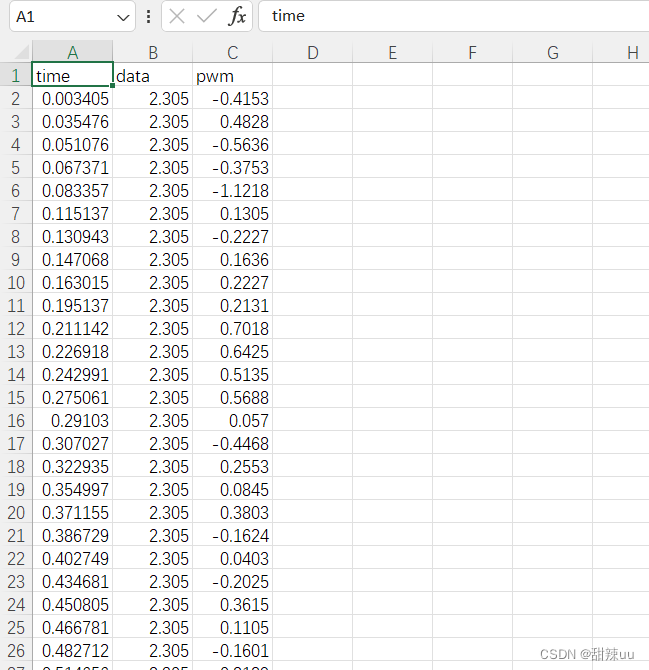
RNN+LSTM正弦sin信号预测 完整代码数据视频教程
视频讲解:RNN+LSTM正弦sin信号预测_哔哩哔哩_bilibili 效果演示: 数据展示: 完整代码: import torch import torch.nn as nn import torch.optim as optim import numpy as np import matplotlib.pyplot as plt import pandas as pd from sklearn.preprocessing import…...
bpmn-js开启只读状态)
如何自己实现一个丝滑的流程图绘制工具(四)bpmn-js开启只读状态
背景 流程图需要支持只读状态和编辑状态 翻看官方案例源码,扒拉到了禁用的js代码 DisableModeling.js const TOGGLE_MODE_EVENT toggleMode const HIGH_PRIORITY 10001export default function DisableModeling(eventBus,contextPad,dragging,directEditing,e…...

字节跳动 Git 的正确使用姿势与最佳实践
版本控制Git 黑马&尚硅谷 Git的前世今生 方向介绍 为什么要学习Git 1.0 Git是什么 1.1 版本控制 1.1.1 本地版本控制 1.1.2 集中版本控制 1.1.3 分布式版本控制 我们已经把三个不同的版本控制系统介绍完了,Git 作为分布式版本控制工具, 虽然目前来讲…...
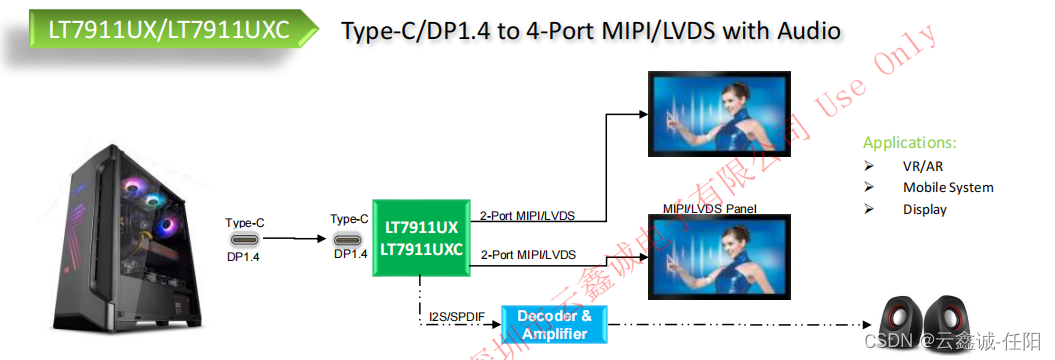
龙迅LT7911UX TYPE-C/DP转MIPI/LVDS,内有HDCP
1. 描述 LT7911UX是一种高性能的Type-C/DP1.4a到MIPI或LVDS芯片。HDCP RX作为HDCP中继器的上游端,可以与其他芯片的HDCP TX协同工作,实现中继器的功能。 对于DP1.4a输入,LT7911UX可以配置为1/2/4车道。自适应均衡使其适用于长电缆应用&#…...

Spearman Footrule距离
Spearman Footrule距离是一种用于衡量两个排列之间差异的指标。它衡量了将一个排列变换为另一个排列所需的操作步骤,其中每个操作步骤都是交换相邻元素。具体而言,Spearman Footrule距离是每个元素在两个排列中的排名差的绝对值之和。 这个指标的名字中…...

docker 安装 Wordpress 用lnmp搭建出现的故障
第一个故障就是mysql出现的故障了 你起mysql镜像是这么起的导致pid号用不了 docker run --namemysql -d --privileged --device-write-bps /dev/sda:10M -v /usr/local/mysql --net mynetwork --ip 172.20.0.20 mysql:lnmp 解决方法 docker run --namemysql -d --privilege…...

【C++入门到精通】C++入门 —— 继承(基类、派生类和多态性)
阅读导航 前言一、继承的概念及定义1. 继承的概念2.继承的定义⭕定义格式⭕继承关系和访问限定符⭕继承基类成员访问方式的变化 二、基类和派生类对象赋值转换三、继承中的作用域四、派生类的默认成员函数五、继承与友元六、继承与静态成员七、复杂的菱形继承及菱形虚拟继承⭕单…...
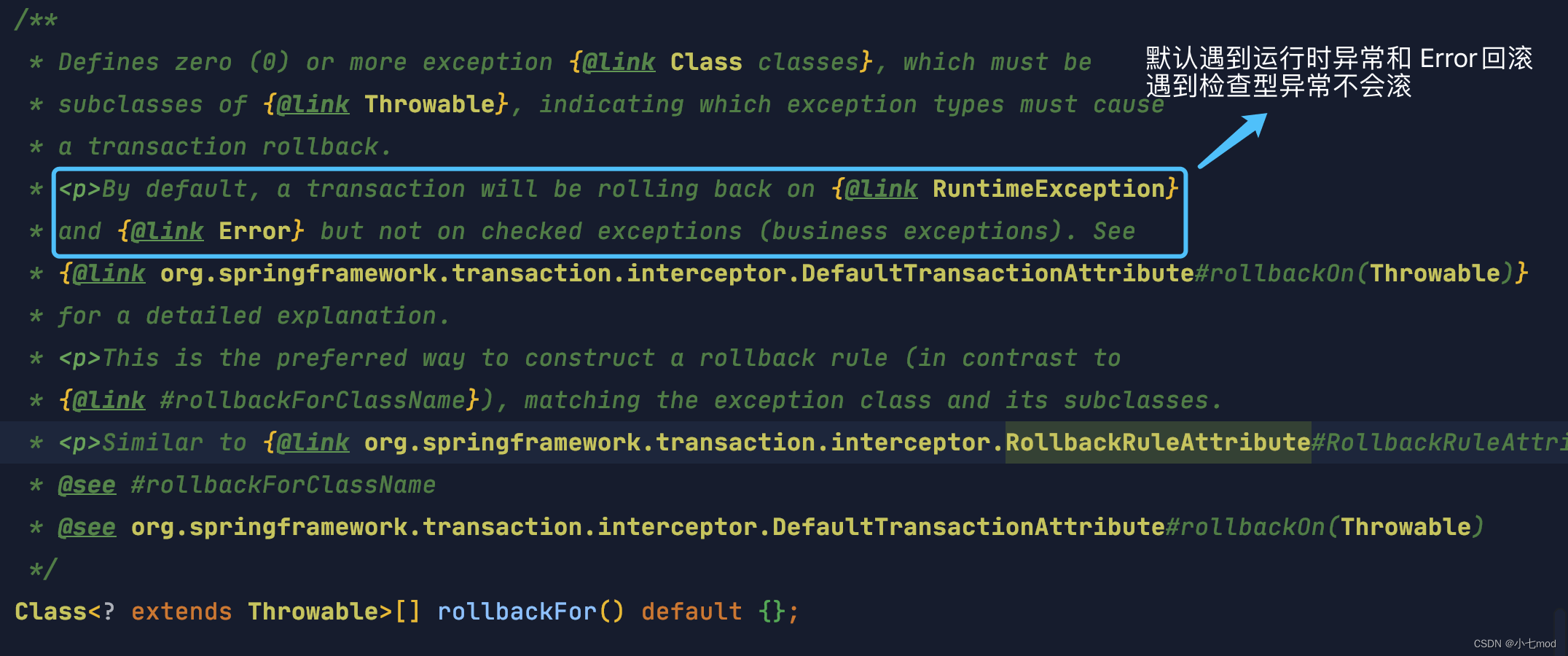
【Spring框架】Spring事务的介绍与使用方法
⚠️ 再提醒一次:Spring 本身并不实现事务,Spring事务 的本质还是底层数据库对事务的支持。你的程序是否支持事务首先取决于数据库 ,比如使用 MySQL 的话,如果你选择的是 innodb 引擎,那么恭喜你,是可以支持…...

七夕特别篇 | 浪漫的Bug
文章目录 前言一、迷失的爱情漩涡(多线程中的错误同步)1.1 Bug 背景1.2 Bug 分析1.3 Bug 解决 二、心形积分之恋(心形面积计算中的数值积分误差)1.1 Bug 背景1.1.1 背景1.1.2 数学模型 1.2 Bug 分析1.2.1 初始代码1.2.2 代码工作流…...
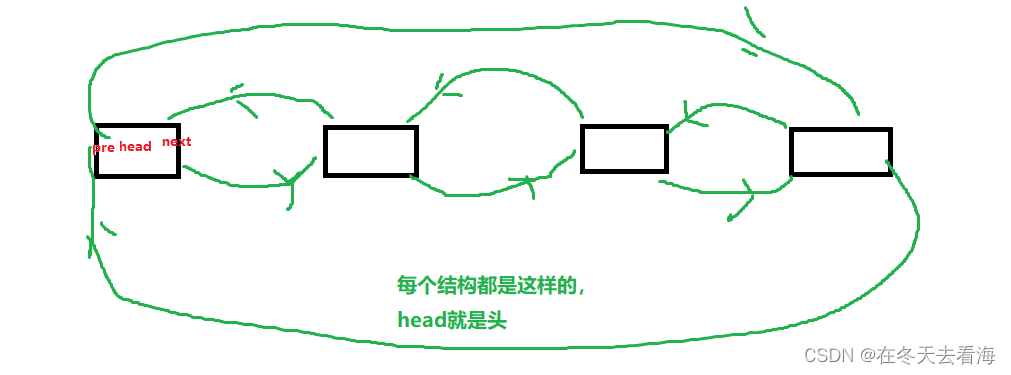
数据结构双向链表
Hello,好久不见,今天我们讲链表的双向链表,这是一个很厉害的链表,带头双向且循环,学了这个链表,你会发现顺序表的头插头删不再是一个麻烦问题,单链表的尾插尾删也变得简单起来了,那废…...
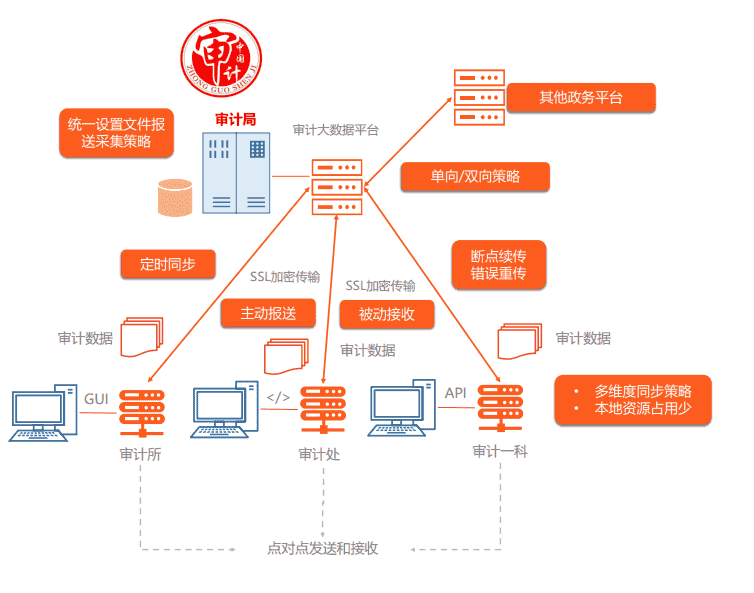
解决政务审计大数据传输难题!镭速传输为政务行业提供解决方案
政务行业是国家治理的重要组成部分,涉及到国家安全、社会稳定、民生福祉等方面。随着信息技术的快速发展和革新,政务信息化也迎来了新一轮的升级浪潮。国家相继出台了《国家信息化发展战略纲要》《“十三五”国家信息化规划》《“十四五”推进国家政务信…...
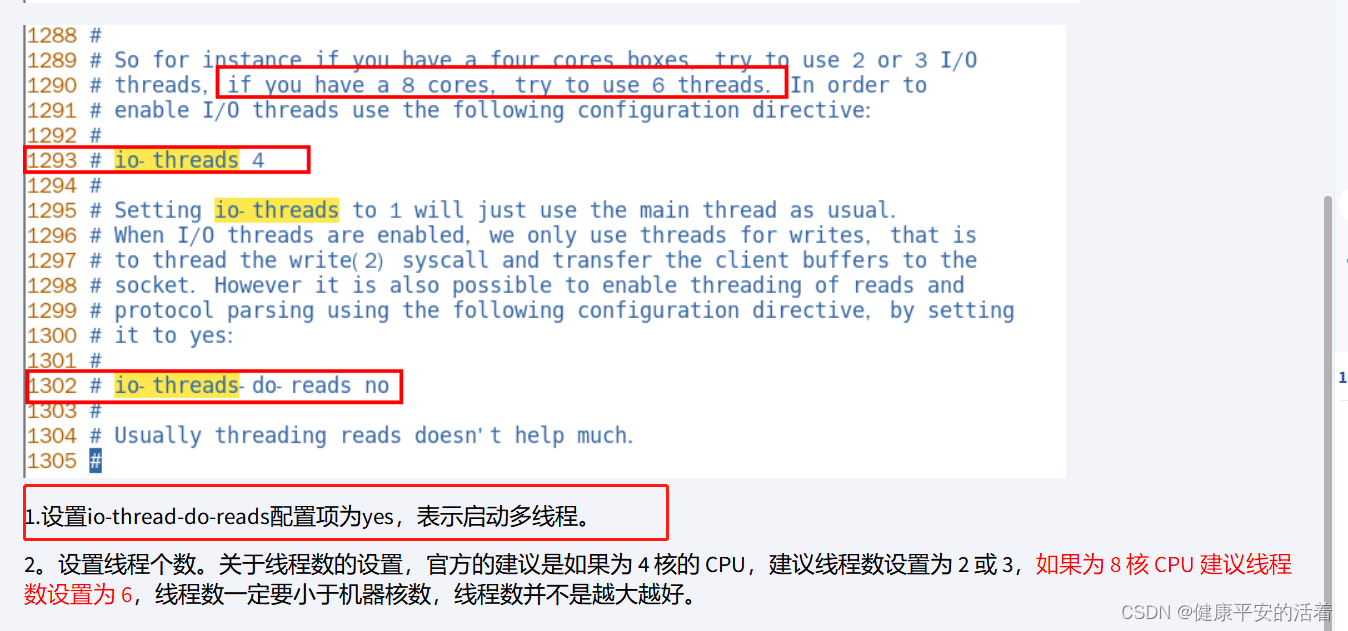
redis 7高级篇1 redis的单线程与多线程
一 redis单线程与多线程 1.1 redis单线程&多线程 1.redis的单线程 redis单线程主要是指Redis的网络IO和键值对读写是由一个线程来完成的,Redis在处理客户端的请求时包括获取 (socket 读)、解析、执行、内容返回 (socket 写) 等都由一个顺序串行的主线程处理…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...
