n-皇后问题(DFS)
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
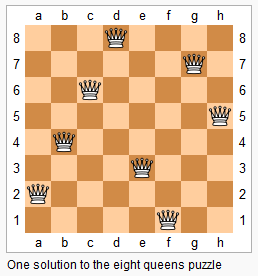
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4
输出样例:
.Q..
...Q
Q...
..Q...Q.
Q...
...Q
.Q..这题的难度就在于对于斜边的判定处理,解释放在代码里,这里直接给出代码
代码如下:
1.第一种方式(在看懂题意下可以知道每行只能放一个皇后,这样写代码更简单时间复杂度,推荐)
//第一种搜索方式
#include<iostream>
using namespace std;
const int N=20;
int n;
char g[N][N];
//由于国际象棋皇后的十字方向以及斜方向都能走,因此每行只能放一个皇后,定义一个行数组xiaochou,正斜线xie,反斜线fxie
bool xiaochou[N],xie[N],fxie[N];void dfs(int u)//u表示遍历到数组第u行
{if(u==n)//当遍历到第n-1行时已经进行完成,等于n直接输出{for(int i=0;i<u;i++) puts(g[i]);puts("");return;}for(int i=0;i<n;i++){if(!xiaochou[i]&&!xie[u+i]&&!fxie[n-u+i])//这里运用到一个数学知识,正对角线该点为u+i,其交叉对于的反对角线为n-u+i{g[u][i]='Q';xiaochou[i]=xie[u+i]=fxie[n-u+i]=true;dfs(u+1);xiaochou[i]=xie[u+i]=fxie[n-u+i]=false;//记得回溯g[u][i]='.';}}
}
int main()
{cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++) g[i][j]='.';}dfs(0);return 0;
}2.第二种方式(一个格子一个格子去枚举判断,比较容易理解,但时间复杂度要大一点)
#include<iostream>
using namespace std;
const int N=20;
int n;
char g[N][N];
//由于国际象棋皇后的十字方向以及斜方向都能走,第二种方法就是把每个格子都枚举一遍
//设置row行数组,col列数组以及两个对角线数组,来判断皇后能不能放
bool row[N],col[N],xie[N],fxie[N];void dfs(int x,int y,int s)//x和y分别表示枚举该数组到啥位置的行列坐标,s表示已经放了几个皇后
{if(y==n) y=0,x++;//每行列举完最后一列的时候,跳到下一行的第一列if(x==n){if(s==n){for(int i=0;i<n;i++) puts(g[i]);puts("");}return;}//不放皇后dfs(x,y+1,s);//放皇后if(!row[x]&&!col[y]&&!xie[x+y]&&!fxie[x-y+n]){g[x][y]='Q';row[x]=col[y]=xie[x+y]=fxie[x-y+n]=true;dfs(x,y+1,s+1);row[x]=col[y]=xie[x+y]=fxie[x-y+n]=false;g[x][y]='.';}
}
int main()
{cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++) g[i][j]='.';}dfs(0,0,0);return 0;
}
难点总结:
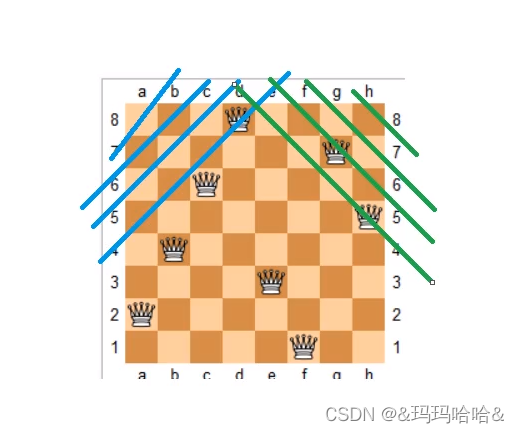
这题需要补充的知识点就是关于对角线如何处理的问题,这里设置正对角线数组和反对角线数组来处理,正对角线为蓝色下标从左上角开始,反对角线为绿色下标从右上角开始,这里因为只要对角线中有一个皇后剩下的都不能放,所以可以看成一个bool类型的一维数组,而难处也在于bool数组的下标应该如何设置,
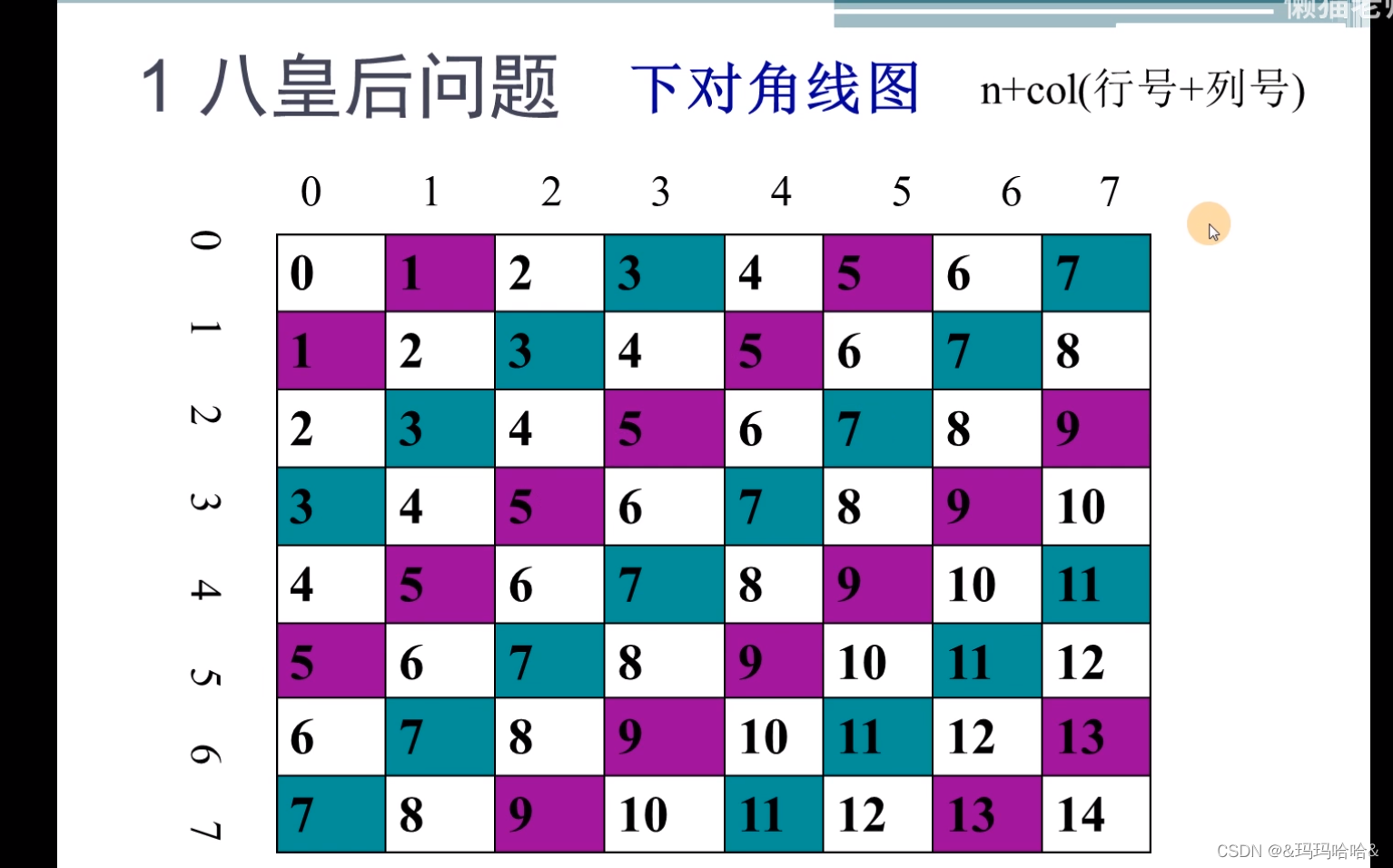
对于正对角线(如下图),规律就是其对角线格子横坐标加上纵坐标相等,因此代码中为x+y,
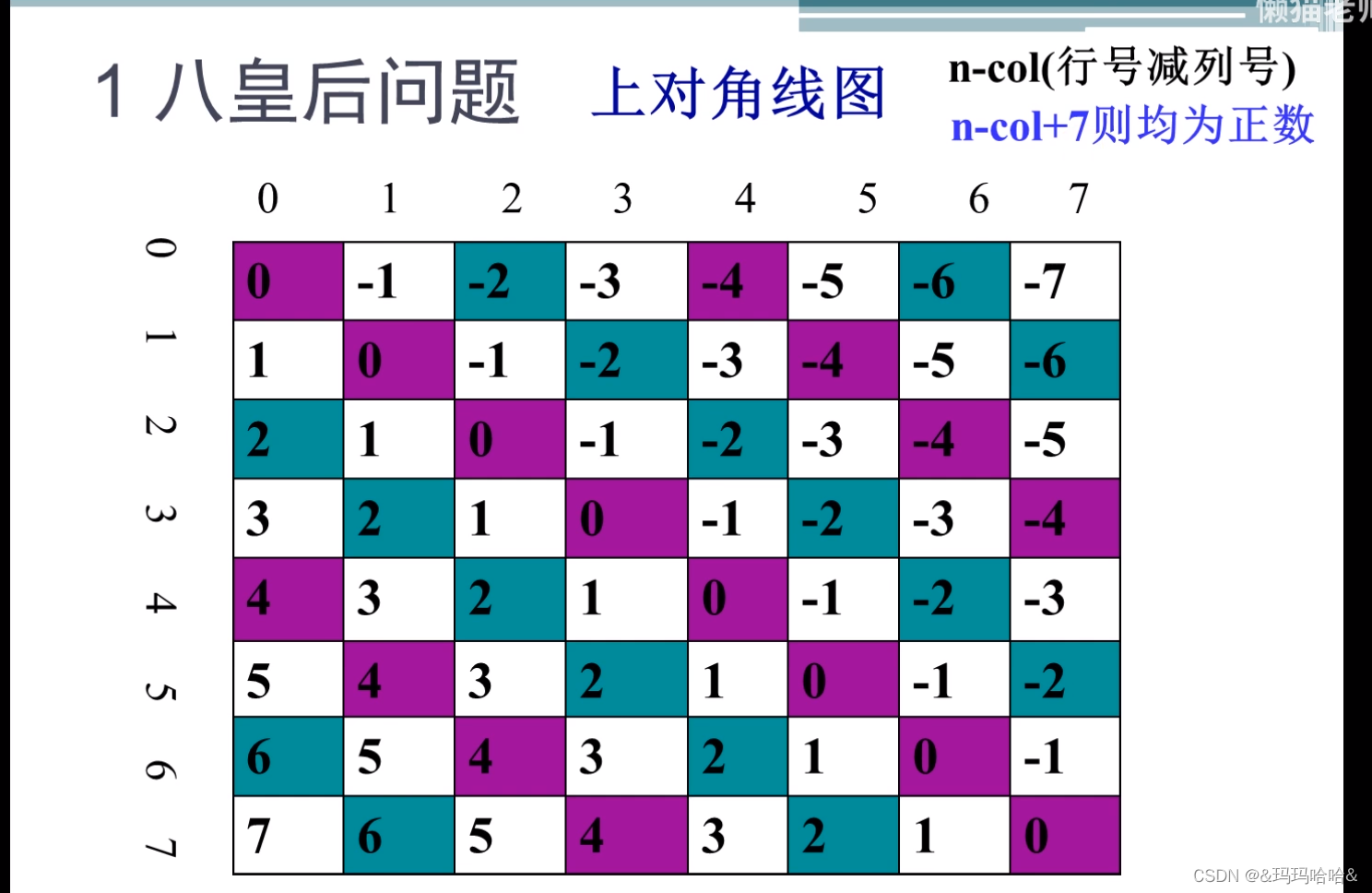
对于反对角线,为x-y+n,这里加n是为了不出现负数
相关文章:

n-皇后问题(DFS)
n−皇后问题是指将 n 个皇后放在 nn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 n,请你输出所有的满足条件的棋子摆法。 输入格式 共一行,包含整数 n。 输出…...

漏洞利用和权限提升
使用Kali Linux进行漏洞利用和权限提升是渗透测试过程中的一部分,用于评估系统的安全性。 漏洞利用: 选择目标: 首先,确定 要进行漏洞利用的目标系统。这可能是一个具有已知漏洞的应用程序、服务或操作系统。 收集信息ÿ…...

开源网安受邀参加软件供应链安全沙龙,推动企业提升安全治理能力
8月23日下午,合肥软件行业软件供应链安全沙龙在中安创谷科技园举办。此次沙龙由合肥软件产业公共服务中心联合中安创谷科技园公司共同主办,开源网安软件供应链安全专家王晓龙、尹杰受邀参会并带来软件供应链安全方面的精彩内容分享,共同探讨…...

回归分析扫盲:为什么非线性模型不能直接用最优子集选择法
最近有人给我发了篇文章: 一个问题有一堆变量,我们要选取哪些变量来建模呢?我们来看看这篇文章是怎么做的: 这个方法简单来说就是:对于这一堆变量,我们每次尝试剔除其中一个变量,然后用剩下的变…...

单例模式简介
概念: 单例模式(Singleton Pattern)是一种创建型设计模式,它确保一个类只有一个实例,并提供全局访问点。单例模式的核心思想是限制某个类只能创建一个对象实例,并提供对该实例的全局访问。这样可以避免多个…...
WPF自定义命令及属性改变处理
1、项目建构 2、自定义命令 namespace WpfDemo.Base {public class MyCommand : ICommand{Action executeAction;public MyCommand(Action action){executeAction action;}public event EventHandler? CanExecuteChanged;public bool CanExecute(object? parameter){retu…...

macbook m1 docker中使用go
已经有一个centos8的镜像,本来打算在centos8中安装go 安装方法: # 1.下载go的安装包 mkdir install && cd install # 任意创建个文件夹 wget https://go.dev/dl/go1.20.2.linux-amd64.tar.gz# 2. 解压 tar -C xzf go1.20.2.linux-amd64.tar.g…...
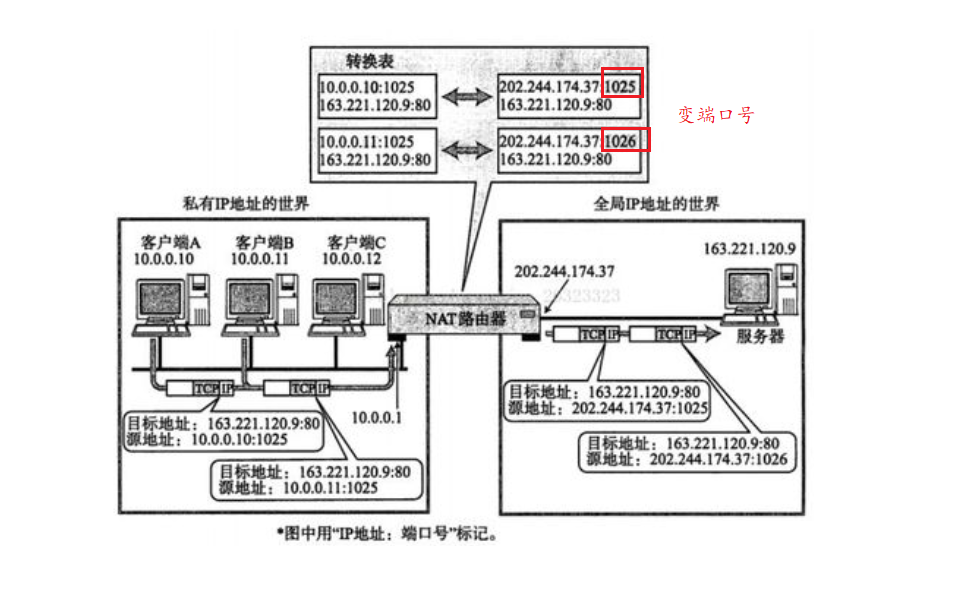
【Hello Network】DNS协议 NAT技术 代理服务器
本篇博客简介:介绍DNS协议 NAT技术和代理服务器 网络各协议补充 DNSDNS背景DNS介绍DNS总结域名简介 NAT技术NAT技术背景NAT IP转换过程NAPTNAT技术缺陷NAT和代理服务器 网络协议总结应用层传输层网络层数据链路层 DNS DNS是一整套从域名映射到IP的系统 DNS背景 为…...
Android 使用模拟器模拟Linux操作系统
1. 简介 在Android手机上使用模拟器模拟ubuntu等操作系统,便于测试 2. 软件准备 Termux:是一款 Android 终端模拟器和 Linux 环境应用程序,无需 root 或设置即可直接运行。虽然酷安和谷歌菜市场都能下载,但这些渠道都很久没更新…...

机器学习基础之《分类算法(5)—朴素贝叶斯算法原理》
一、朴素贝叶斯算法 1、什么是朴素贝叶斯分类方法 之前用KNN算法,分类完直接有个结果,但是朴素贝叶斯分完之后会出现一些概率值,比如: 这六个类别,它都有一定的可能性 再比如,对文章进行分类:…...

# Go学习-Day6
文章目录 Go学习-Day6封装继承接口 Go学习-Day6 个人博客:CSDN博客 封装 类似java的类的封装,这里我们利用大小写和工厂模式来实现封装的功能略过 继承 相似的类具有相似的方法,反复绑定相同的方法,代码冗余,所以引…...
分布式 - 服务器Nginx:一小时入门系列之 HTTPS协议配置
文章目录 1. HTTPS 协议2. 生成 SSL 证书和私钥文件3. 配置 SSL 证书和私钥文件4. HTTPS 协议优化 1. HTTPS 协议 HTTPS 是一种通过计算机网络进行安全通信的协议。它是HTTP的安全版本,通过使用 SSL 或 TLS 协议来加密和保护数据传输。HTTPS的主要目的是确保在客户…...

探秘Linux系统性能监控神器!Linux和Python技术持续学习者必看!
引言 作为Linux运维工程师,我们经常需要对服务器的性能进行监控和调优。而Python作为一门强大的脚本语言,可以帮助我们轻松实现各种系统性能监控任务。本文将介绍几个实用的Python库和工具,帮助我们监控Linux系统的CPU、内存、磁盘和网络等性…...

文心一言续写太监小说《名侦探世界的巫师》
《名侦探世界的巫师》是我的童年回忆,总是想着续写一下,但是又没有时间和文笔,文心一言出了,由于目前大模型貌似可以联网,可以尝试搞一波~ 目录 文章1【前六个故事还能看,后面就是在重复】故事2【辣眼睛】…...
)
Solidity 合约安全,常见漏洞(第三篇)
Solidity 合约安全,常见漏洞(第三篇) ERC20 代币问题 如果你只处理受信任的 ERC20 代币,这些问题大多不适用。然而,当与任意的或部分不受信任的 ERC20 代币交互时,就有一些需要注意的地方。 ERC20&#…...
Linux安装Redis数据库,无需公网IP实现远程连接
文章目录 1. Linux(centos8)安装redis数据库2. 配置redis数据库3. 内网穿透3.1 安装cpolar内网穿透3.2 创建隧道映射本地端口 4. 配置固定TCP端口地址4.1 保留一个固定tcp地址4.2 配置固定TCP地址4.3 使用固定的tcp地址连接 Redis作为一款高速缓存的key value键值对的数据库,在…...

智慧政务,长远布局——AIGC引领,加速推进数字化政府建设
在人工智能、虚拟现实等领域迅猛发展且日益成熟的背景下,AI行业正迈向蓬勃发展的全新阶段,市场规模持续扩张。与此同时,数字服务也正在蓬勃兴起,新一代信息技术为数字政府构建了坚实支撑,重塑了政务信息化管理、业务架…...
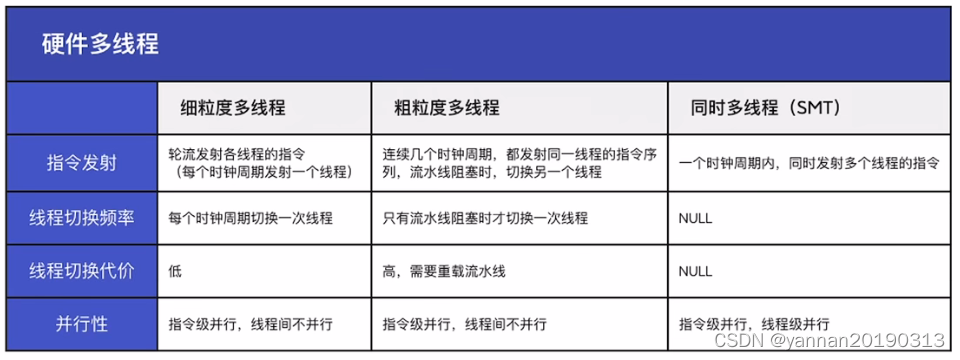
中央处理器(CPU):组成、指令周期、数据通路、控制方式、控制器、指令流水线,补充(多处理器系统、硬件多线程)
中央处理器(CPU,Central Processing Unit),计算机控制和运算的核心,是信息处理和程序运行的执行单元。 CPU主要功能:处理指令、执行操作、控制时间、处理中断、处理数据。 其中,处理指令、执行…...

开源微服务如何选型?Spring Cloud、Dubbo、gRPC、Istio 详细对比
作者:刘军 不论您是一名开发者、架构师、CTO, 如果您曾深度参与在微服务开发中,那么相信您一定有过开源微服务框架或体系选型的疑问:Apache Dubbo、Spring Cloud、gRPC 以及 Service Mesh 体系产品如 Istio,到底应该选…...

Nginx的HTTPS部署与安全性能优化
Nginx作为一款高性能的Web服务器和反向代理服务器,被广泛用于应用部署和负载均衡。在安全环保意识的逐渐提高下,HTTPS也成为现代Web应用中必不可少的一环。本篇文章将重点介绍Nginx的HTTPS部署和安全性能优化。 一、Nginx的HTTPS部署 证书申请 首先需要去…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
