激活函数总结(二十):激活函数补充(SQNL、PLU)
激活函数总结(二十):激活函数补充
- 1 引言
- 2 激活函数
- 2.1 Square nonlinearity (SQNL)激活函数
- 2.2 Piecewise Linear Unit (PLU)激活函数
- 3. 总结
1 引言
在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、Leaky ReLU、PReLU、Swish、ELU、SELU、GELU、Softmax、Softplus、Mish、Maxout、HardSigmoid、HardTanh、Hardswish、HardShrink、SoftShrink、TanhShrink、RReLU、CELU、ReLU6、GLU、SwiGLU、GTU、Bilinear、ReGLU、GEGLU、Softmin、Softmax2d、Logsoftmax、Identity、LogSigmoid、Bent Identity、Absolute、Bipolar、Bipolar Sigmoid、Sinusoid、Cosine、Arcsinh、Arccosh、Arctanh、LeCun Tanh、TanhExp、Gaussian 、GCU、ASU、SQU、NCU、DSU、SSU、SReLU、BReLU、PELU、Phish、RBF、SQ-RBF、ISRU、ISRLU)。在这篇文章中,会接着上文提到的众多激活函数继续进行介绍,给大家带来更多不常见的激活函数的介绍。这里放一张激活函数的机理图:

2 激活函数
2.1 Square nonlinearity (SQNL)激活函数
Square nonlinearity(SQNL)一种新的计算高效激活函数。由于其固有的平方运算,该函数被命名为平方律非线性(SQNL)函数。其数学表达式和数学图像分别如下所示:
S Q N L ( x ) = { 1 , if x > 2 x − x 2 4 , if 0 ≤ x ≤ 2 x + x 2 4 , if − 2 ≤ x < 0 − 1 , if x < − 2 SQNL(x) = \begin{cases} 1, & \text{if } x > 2 \\ x - \frac{x^2}{4}, & \text{if } 0 \leq x \leq 2 \\ x + \frac{x^2}{4}, & \text{if } -2 \leq x < 0 \\ -1, & \text{if } x < -2 \\ \end{cases} SQNL(x)=⎩ ⎨ ⎧1,x−4x2,x+4x2,−1,if x>2if 0≤x≤2if −2≤x<0if x<−2
优点:
- 简单非线性:
平方运算,一个最简单的非线性操作。 - 对称和连续:它在
零附近是对称的,在−∞和+∞之间是连续的。 - 线性微分:SQNL的
导数是线性的。
缺点:
- 可解释性: SQNL不是一个
广泛使用的激活函数,因此可能需要更多的背景知识来解释其作用和效果。 - 过于简单:很难用于处理
复杂问题,提取复杂问题中的关键特征。
SQNL是一个用于数字电路的激活函数,在FPGA中有所用到。。。但是在深度学习中很少出现。。。。
2.2 Piecewise Linear Unit (PLU)激活函数
论文链接:https://arxiv.org/pdf/1809.09534v1.pdf
PLU是一种类似于 ReLU 的激活函数,但在负半部分采用了分段线性变换,以引入更多的非线性性质。其数学表达式和数学图像分别如下所示:
P L U ( x ) = m a x ( α ( x + c ) − c , m i n ( α ( x + c ) + c , x ) ) PLU(x)=max(\alpha (x+c)-c, min(\alpha (x+c)+c, x)) PLU(x)=max(α(x+c)−c,min(α(x+c)+c,x))
优点:
- 非线性性质: PLU 引入了
非线性性质,有助于神经网络捕捉数据中的复杂模式,使其在处理非线性问题时表现更好。 - 平滑性: 在输入范围内,PLU 是
分段线性的,有助于梯度计算的稳定性,减少了梯度突变可能引发的问题。 - 参数调节: 通过
调整参数 α 和 c,可以控制 PLU 激活函数的斜率和平移,使其适应不同任务和数据分布。
缺点:
- 参数设置: 需要仔细调整参数 α 和 c 才能获得
最佳性能,这可能需要一些实验和调试。 - 可解释性: PLU 不是最
常见的激活函数之一,可能需要更多的背景知识来理解其作用和效果。
总之,PLU 激活函数通过引入分段线性特性,同时保持一定的平滑性,旨在增加神经网络的非线性能力。但是,这是这种不常见的性质导致其并不常使用。。。。。
3. 总结
到此,使用 激活函数总结(二十) 已经介绍完毕了!!! 如果有什么疑问欢迎在评论区提出,对于共性问题可能会后续添加到文章介绍中。如果存在没有提及的激活函数也可以在评论区提出,后续会对其进行添加!!!!
如果觉得这篇文章对你有用,记得点赞、收藏并分享给你的小伙伴们哦😄。
相关文章:

激活函数总结(二十):激活函数补充(SQNL、PLU)
激活函数总结(二十):激活函数补充 1 引言2 激活函数2.1 Square nonlinearity (SQNL)激活函数2.2 Piecewise Linear Unit (PLU)激活函数 3. 总结 1 引言 在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、Leaky ReLU、PR…...
使用说明分享)
Docker【部署 04】Docker Compose下载安装及实例Milvus Docker compose(CPU)使用说明分享
Docker Compose 下载安装使用说明 1.Compose说明1.1 Overview of installing Docker Compose1.2 Installation scenarios1.2.1 Scenario one: Install Docker Desktop1.2.2 Scenario two: Install the Compose plugin1.2.3 Scenario three: Install the Compose standalone 2.C…...

23种设计模式-7种结构模式
结构型模式简述 把类或对象结合在一起形成一个更大的结构。 装饰器模式:动态的给对象添加新的功能。 代理模式:为其它对象提供一个代理以便控制这个对象的访问。 桥接模式:将抽象部分和它的实现部分分离,使它们都可以独立的变…...

大数据Flink(六十七):SQL Table 简介及运行环境
文章目录 SQL & Table 简介及运行环境 一、简介 二、案例...

WPF使用依赖注入
现在依赖注入在.Net里面已经普及,自己常写一些简单的demo倒是无所谓,但偶尔写一点正式的工程,也免不了要使用一下,于是总结了一下在WPF里面使用依赖注入。 在写简单Demo时候,通常是在MainWindow的构造函数里面直接做初…...
玩转科技|了解AI平台桌面客户端—ChatBox
目录 前言 特性 编辑 为什么需要 ChatBox? ChatGPT Plus 平替? 下载 支持系统 功能图 使用教程 感受 展示 前言 今天小编又来了,推荐给大家一款开源的OpenAI API桌面客户端ChatBox,它支持 Windows、Mac 和 Linux。…...

visual studio 2022.NET Core 3.1 未显示在目标框架下拉列表中
问题描述 在Visual Studio 2022我已经安装了 .NET core 3.1 并验证可以运行 .NET core 3.1 应用程序,但当创建一个新项目时,目标框架的下拉列表只允许 .NET 6.0和7.0。而我在之前用的 Visual Studio 2019,可以正确地添加 .NET 核心项目。 …...

人工智能项目集合推荐(数据集 模型训练 C++和Android部署)
人工智能项目集合推荐(数据集 模型训练 C和Android部署) 目录 人工智能项目集合推荐(数据集 模型训练 C和Android部署) 1.三维重建项目集合 ★双目三维重建 ★结构光三维重建 2.AI CV项目集合 ★人脸检测和人体检测 ★人体姿态估计(人体关键点检测) ★头部朝向估计 …...

C# 服务HTTPS 对 请求被中止: 未能创建 SSL/TLS 安全通道报错
1.如果windows支持HTTPS的TLS协议,则可以直接跳过 (Tls12) [WebMethod(Description "获取HttpsPost加密服务.")] public string HTTPSPOST(String input,String sUrl) { Log.Add("ReceiveNotice", &qu…...
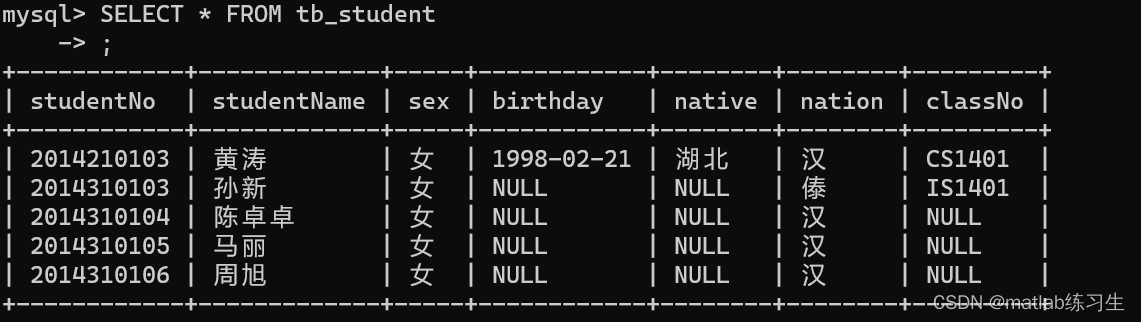
二级MySQL(七)——表格数据修改
1、修改表格中部分数据 将表格某一行的数据修改,这里用的UPDATE语句: UPDATE tb_student SET studentName 黄涛,native湖北,nation汉 WHERE studentNo 2014210103; 结果: 2、修改表格某一列全部数据 比如性别全部设置为‘女’ UPDATE…...

【日常积累】Linux下sftp搭建
概述 SFTP是Secure File Transfer Protocol的缩写,是安全文件传送协议。可以为传输文件提供一种安全的加密方法。跟ftp几乎语法功能一样。 SFTP是SSH的一部分,是一种传输档案至Blogger伺服器的安全方式。它本身没有单独的守护进程,必须使用s…...

【深入浅出C#】章节 9: C#高级主题:多线程编程和并发处理
多线程编程和并发处理的重要性和背景 在计算机科学领域,多线程编程和并发处理是一种关键技术,旨在充分利用现代计算机系统中的多核处理器和多任务能力。随着计算机硬件的发展,单一的中央处理单元(CPU)已经不再是主流&a…...

Windows Server服务器安全加固基线配置
一、账户管理、认证授权 一、账户 1、管理缺省账户 安全基线项说明:对于管理员账号,要求更改缺省账户名称;禁用Guest(来宾)账户。 操作步骤:进入控制面板-->管理工具-->计算机管理,在系统工具-->本地用户和组…...
)
基于NXP i.MX 6ULL核心板的物联网模块开发案例(4)
目录 5 4G模块测试 5.1 网络功能测试 5.2 短信功能测试 5.3 通话功能测试 5.4 GPS定位功能测试 5.5 程序编译 前言 本文主要介绍基于创龙科技TLIMX6U-EVM评估板的物联网模块开发案例,适用开发环境: Windows开发环境:Windows 7 64bit、Windows 10 64bit 虚拟机:VMware15.…...

英语——强调
强调句是英语中常用的一个重点句型,其基本结构是:It+be+被强调部分+that+句子其余部分。 第一节 强调句的基本用法 一、被强调的句子成分 在强调句型中,能够被强调的句子成分通常为主语、宾语、状语等,不能用来强调谓语动词、表语、补语、让步状语、条件状语等。当被强调…...
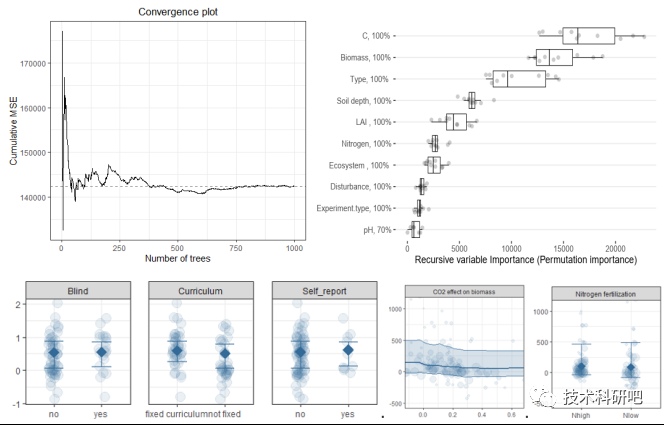
全流程R语言Meta分析核心技术教程
详情点击链接:全流程R语言Meta分析核心技术教程 一,Meta分析的选题与检索 1、Meta分析的选题与文献检索 1)什么是Meta分析? 2)Meta分析的选题策略 3)精确检索策略,如何检索全、检索准 4)文献的管理与清洗,如何制定文…...
【C++精华铺】9.STL string
目录 1. string类的优势 2. string类的常用接口 2.1 常用构造 1. 空串构造:string(); 2. C串构造:string(const char* s); 3. 拷贝构造:string(const string& str); 4. 字符填充构造:string(size_t n, char c); 5. 迭代…...

【PACS】医学影像管理系统源码带三维重建后处理技术
PACS系统,意为影像归档和通信系统。它是应用在医院影像科室的系统,主要的任务就是把日常产生的各种医学影像(包括核磁,CT,超声,各种X光机,各种红外仪、显微仪等设备产生的图像)通过各…...

从0开始学go 第一天
今天是开始学go的第x天,前些日子看了看语言,今天找一个web开发来跟着学,记录一下遇到的问题,方便以后复习查阅。 视频看的是https://www.bilibili.com/video/BV1gJ411p7xC?p3&vd_sourceab5bdbd04f4142027c66d604d5285204 视…...

Spring Cloud Nacos详解
目录 1、Spring Cloud Nacos详细介绍2、Spring Cloud Nacos具体案列 Spring Cloud Nacos 是一个由阿里巴巴集团开发的开源分布式系统服务发现、配置管理和服务管理的平台。Nacos 支持多种服务发现方式,包括 DNS 方式、HTTP 和 RPC 方式,同时提供了灵活的…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
