概率论作业啊啊啊
1 数据位置 (Measures of location)
对于数据集: 7 , 9 , 9 , 10 , 10 , 11 , 11 , 12 , 12 , 12 , 13 , 14 , 14 , 15 , 16 7,9,9,10,10,11,11,12,12,12,13,14,14,15,16 7,9,9,10,10,11,11,12,12,12,13,14,14,15,16
- 计算加权平均数,其中权重为: 2 , 1 , 3 , 2 , 1 , 1 , 2 , 2 , 1 , 3 , 2 , 1 , 1 , 1 , 1 2,1,3,2,1,1,2,2,1,3,2,1,1,1,1 2,1,3,2,1,1,2,2,1,3,2,1,1,1,1
- 计算截断均值, 去除最高和最低的两个值。
- 计算众数,中位数
2 数据散布(Measures of spread/dispersion)
使用上述数据集,计算四分位差
3 随机变量的类型和概率分布
考虑一个实验,其中一个包包含 5 个红球和 3 个绿球。随机从中抽取 2 个球,不放回。定义一 个随机变量 X X X 为抽取的红球数量。列出 X X X 的所有可能值,并为每个值计算概率。
4 理论概率分布之常见的离散型分布
一个生产线上,产品的不合格率为 0.05 。现在从生产线上随机选择10个产品。使用二项分布 计算恰好有 2 个不合格产品的概率。
5 假设学生的智商(IQ)分数分布是标准正态分布,平均值为100,标准差为15。计算以下情况的概率:
一个随机选择的学生的IQ分数高于125的概率。
一个随机选择的学生的IQ分数在85到115之间的概率。
一个随机选择的学生的IQ分数低于70或高于130的概率。
答案
- 数据位置 (Measures of location)
答案:
- 加权平均数 = 11.25 =11.25 =11.25
- 截断均值 = 11.69 =11.69 =11.69
- 数据散布 (Measures of spread/dispersion)
答案:
- 四分位差 = 3.5 =3.5 =3.5
- 方差 = 5.69 =5.69 =5.69
- 标准差 = 2.39 =2.39 =2.39
- 众数为 = 12 =12 =12,中位数也为 = 12 =12 =12。
- 随机变量的类型和概率分布
考虑这样一个实验,从一个包含 5 个红球和 3 个绿球的袋子中随机抽取 2 个球,并不放回。我们 定义一个随机变量 X X X 来表示抽取的红球数量。我们可以为 X X X 的每个可能值计算概率。
P ( X = 0 ) P(X=0) P(X=0) : 抽取两个球都是绿色的。
这个概率可以这样计算:
首先,第一个球是绿色的概率是 3 8 \frac{3}{8} 83 。
接着,第二个球也是绿色的概率是 2 7 \frac{2}{7} 72 (因为已经有一个绿球被抽出,所以只剩下 2 个绿球和 7 个球总数)。
因此,两次事件的联合概率为: P ( X = 0 ) = 3 8 × 2 7 = 6 56 P(X=0)=\frac{3}{8} \times \frac{2}{7}=\frac{6}{56} P(X=0)=83×72=566 。
P ( X = 1 ) P(X=1) P(X=1) : 抽取的其中一个球是红色,另一个是绿色。
这个概率可以分为两种情况:
第一种情况是首先抽到一个红球,然后抽到一个绿球。概率为 5 8 × 3 7 \frac{5}{8} \times \frac{3}{7} 85×73 。
第二种情况是首先抽到一个绿球,然后抽到一个红球。概率为 3 8 × 5 7 \frac{3}{8} \times \frac{5}{7} 83×75 。
把这两种情况的概率加起来,我们得到: P ( X = 1 ) = 5 8 × 3 7 + 3 8 × 5 7 = 30 56 P(X=1)=\frac{5}{8} \times \frac{3}{7}+\frac{3}{8} \times \frac{5}{7}=\frac{30}{56} P(X=1)=85×73+83×75=5630 。
P ( X = 2 ) P(X=2) P(X=2) : 抽取两个球都是红色的。
这个概率可以这样计算:
首先,第一个球是红色的概率是 5 8 \frac{5}{8} 85 。
接着,第二个球也是红色的概率是 4 7 \frac{4}{7} 74 (因为已经有一个红球被抽出,所以只剩下 4 个红球和 7 个球总数)。
因此,两次事件的联合概率为: P ( X = 2 ) = 5 8 × 4 7 = 20 56 P(X=2)=\frac{5}{8} \times \frac{4}{7}=\frac{20}{56} P(X=2)=85×74=5620 。
- 二项分布
假设我们在生产线上随机选择了10个产品,而每个产品都是独立检查的。因此,每个产品不 合格的概率都是 0.05 ,合格的概率则是 0.95 。
现在,我们想要知道恰好有 2 个产品不合格的概率。我们可以使用二项分布公式来计算这一概 率:
P ( X = k ) = ( n k ) p k ( 1 − p ) n − k P(X=k)=\left(\begin{array}{l} n \\ k \end{array}\right) p^k(1-p)^{n-k} P(X=k)=(nk)pk(1−p)n−k
其中:
- ( n k ) \left(\begin{array}{l}n \\ k\end{array}\right) (nk) 是组合公式,表示从 n \mathrm{n} n 个中选择 k \mathrm{k} k 个的方法数。它的公式是:
( n k ) = n ! k ! ( n − k ) ! \left(\begin{array}{l} n \\ k \end{array}\right)=\frac{n !}{k !(n-k) !} (nk)=k!(n−k)!n! - n n n 是试验次数,此处为 10 。
- k k k 是成功的次数,此处为 2 。
- p p p 是一次试验成功的概率,此处为 0.05 。
将上述值代入公式,我们可以计算得到恰好有 2 个不合格产品的概率。
- 正态分布
对于正态分布的随机变量 X X X ,我们通常使用以下的公式来计算其概率:
P ( a ≤ X ≤ b ) = P ( X ≤ b ) − P ( X ≤ a ) P(a \leq X \leq b)=P(X \leq b)-P(X \leq a) P(a≤X≤b)=P(X≤b)−P(X≤a)
其中, P ( X ≤ b ) P(X \leq b) P(X≤b) 和 P ( X ≤ a ) P(X \leq a) P(X≤a) 可以从正态分布的累积分布函数 (CDF) 中查找。
对于标准正态分布,均值 μ = 0 \mu=0 μ=0 ,标准差 σ = 1 \sigma=1 σ=1 。但在这个例子中,我们的分布不是标准 的,所以我们需要先将其转换为标准正态分布。这可以通过以下的公式实现:
Z = X − μ σ Z=\frac{X-\mu}{\sigma} Z=σX−μ
其中 Z Z Z 是标准正态分布的随机变量。
计算一个随机选择的学生的IQ分数高于125的概率:
首先, 我们将 I Q = 125 I Q=125 IQ=125 转换为标准正态变量:
Z = 125 − 100 15 Z=\frac{125-100}{15} Z=15125−100
接着,我们查找标准正态分布表 (或使用计算工具) 来找到 Z Z Z 对应的概率 P ( Z ) P(Z) P(Z) 。 最后,我们使用 P ( X > 125 ) = 1 − P ( Z ) P(X>125)=1-P(Z) P(X>125)=1−P(Z) 来得到所求的概率。
计算一个随机选择的学生的IQ分数在85到115之间的概率:
我们首先将 ∣ Q = 85 \mid Q=85 ∣Q=85 和 ∣ Q = 115 \mid \mathrm{Q}=115 ∣Q=115 都转换为标准正态变量:
Z 1 = 85 − 100 15 Z 2 = 115 − 100 15 \begin{aligned} & Z_1=\frac{85-100}{15} \\ & Z_2=\frac{115-100}{15} \end{aligned} Z1=1585−100Z2=15115−100
然后,我们查找标准正态分布表来找到 Z 1 Z_1 Z1 和 Z 2 Z_2 Z2 对应的概率 P ( Z 1 ) P\left(Z_1\right) P(Z1) 和 P ( Z 2 ) P\left(Z_2\right) P(Z2) 。 最后,我们使用上面的公式来计算 P ( 85 ≤ X ≤ 115 ) = P ( Z 2 ) − P ( Z 1 ) P(85 \leq X \leq 115)=P\left(Z_2\right)-P\left(Z_1\right) P(85≤X≤115)=P(Z2)−P(Z1) 。
计算一个随机选择的学生的IQ分数低于70或高于 130 的概率:
我们首先将 1 Q = 70 1 \mathrm{Q}=70 1Q=70 和 ∣ Q = 130 \mid \mathrm{Q}=130 ∣Q=130 都转换为标准正态变量:
Z 1 = 70 − 100 15 Z 2 = 130 − 100 15 \begin{aligned} & Z_1=\frac{70-100}{15} \\ & Z_2=\frac{130-100}{15} \end{aligned} Z1=1570−100Z2=15130−100
然后,我们查找标准正态分布表来找到 Z 1 Z_1 Z1 和 Z 2 Z_2 Z2 对应的概率 P ( Z 1 ) P\left(Z_1\right) P(Z1) 和 P ( Z 2 ) P\left(Z_2\right) P(Z2) 。 最后,我们使用以下的公式来得到所求的概率:
P ( X < 70 or X > 130 ) = P ( Z 1 ) + ( 1 − P ( Z 2 ) ) P(X<70 \text { or } X>130)=P\left(Z_1\right)+\left(1-P\left(Z_2\right)\right) P(X<70 or X>130)=P(Z1)+(1−P(Z2))
基于正态分布的计算结果如下:
一个随机选择的学生的IQ分数高于125的概率是 0.0478 (保留四位小数)。
一个随机选择的学生的IQ分数在85到115之间的概率是 0.6827。
一个随机选择的学生的IQ分数低于70或高于130的概率是 0.0455。
相关文章:

概率论作业啊啊啊
1 数据位置 (Measures of location) 对于数据集: 7 , 9 , 9 , 10 , 10 , 11 , 11 , 12 , 12 , 12 , 13 , 14 , 14 , 15 , 16 7,9,9,10,10,11,11,12,12,12,13,14,14,15,16 7,9,9,10,10,11,11,12,12,12,13,14,14,15,16 计算加权平均数,其中权重为: 2 , 1 , 3 , 2 ,…...

React re-render
What is? react的渲染分为两个阶段: render,组件第一次出现在屏幕上的时候触发re-render, 组件第一次渲染之后的渲染 当app的数据更新时(用户手动更新、或异步请求)。 When? re-render发生有四种可能: state改变…...
从零开始配置Jenkins与GitLab集成:一步步实现持续集成
在软件开发中,持续集成是确保高效协作和可靠交付的核心实践。以下是在CentOS上安装配置Jenkins与GitLab集成的详细步骤: 1.安装JDK 解压JDK安装包并设置环境变量: JDK下载网址 Java Downloads | Oracle 台灣 tar zxvf jdk-11.0.5_linux-x64_b…...
高效多用的群集-Haproxy搭建Web集群
Haproxy搭建 Web 群集 一、Haproxy前言 HAProxy是一个使用c语言编写的自由及开放源代码软件,其提供高可用性、负载均衡,以及基于TcP和HrrP的应用程序代理。HAProxy特别适用于那些负载特大的web站点,这些站点通常又需要会话保持或七层处理。…...

aws的s3匿名公开访问
点击桶权限 ,添加策略 {"Version": "2012-10-17","Statement": [{"Sid": "AddPerm","Effect": "Allow","Principal": "*","Action": "s3:GetObject&qu…...
2023科隆游戏展:虚幻5游戏百花齐放,云渲染助力虚幻5高速渲染
8月23日,欧洲权威级游戏展示会——科隆游戏展拉开帷幕。今年的参展游戏也相当给力,数十款游戏新预告片在展会上公布,其中有不少游戏使用虚幻5引擎制作,开创了游戏开发新纪元。 虚幻5游戏百花齐放,渲染堪比电影级效果 …...

Spark大数据分析与实战笔记(第一章 Scala语言基础-2)
文章目录 章节概要1.2 Scala的基础语法1.2.1 声明值和变量1.2.2 数据类型1.2.3 算术和操作符重载1.2.4 控制结构语句1.2.5 方法和函数 章节概要 Spark是专为大规模数据处理而设计的快速通用的计算引擎,它是由Scala语言开发实现的,关于大数据技术…...

Linux 下 Mysql 的使用(Ubuntu20.04)
文章目录 一、安装二、使用2.1 登录2.2 数据库操作2.2.1 创建数据库2.2.2 删除数据库2.2.3 创建数据表 参考文档 一、安装 Linux 下 Mysql 的安装非常简单,一个命令即可: sudo apt install mysql-server检查安装是否成功,输入: …...
牛客练习赛114
A.最后有0得数肯定是10得倍数,然后直接排序即可 #include<bits/stdc.h> using namespace std; const int N 1e610,mod1e97; int n; void solve(){cin>>n;vector<int> a(n);for(auto&i:a) cin>>i;sort(a.begin(),a.end(),greater<&g…...

Http与Https
1.简单介绍 HTTP:最广泛应用的网络通信协议,基于TCP,数据传输简单高效,数据是明文。 HTTPS:是HTTP的加强版,是HTTPSSL。在HTTP的基础上加了安全机制,一方面保证数据的安全传输,另一…...
前端通信(渲染、http、缓存、异步、跨域)自用笔记
SSR/CSR:HTML拼接?网页源码?SEO/交互性 SSR (server side render)服务端渲染,是指由服务侧(server side)完成页面的DOM结构拼接,然后发送到浏览器,为其绑定状…...

43.227.198.x怎么检查服务器里是否中毒情况?
要检查43.227.198.1服务器是否中毒,可以执行以下步骤: 运行杀毒软件:运行已安装的杀毒软件进行全盘扫描,查看是否有病毒或恶意软件。如果发现病毒或恶意软件,立即将其删除或隔离。 检查系统文件:检查服务器…...
Sentinel dashboard无法查询到应用的限流配置问题以及解决
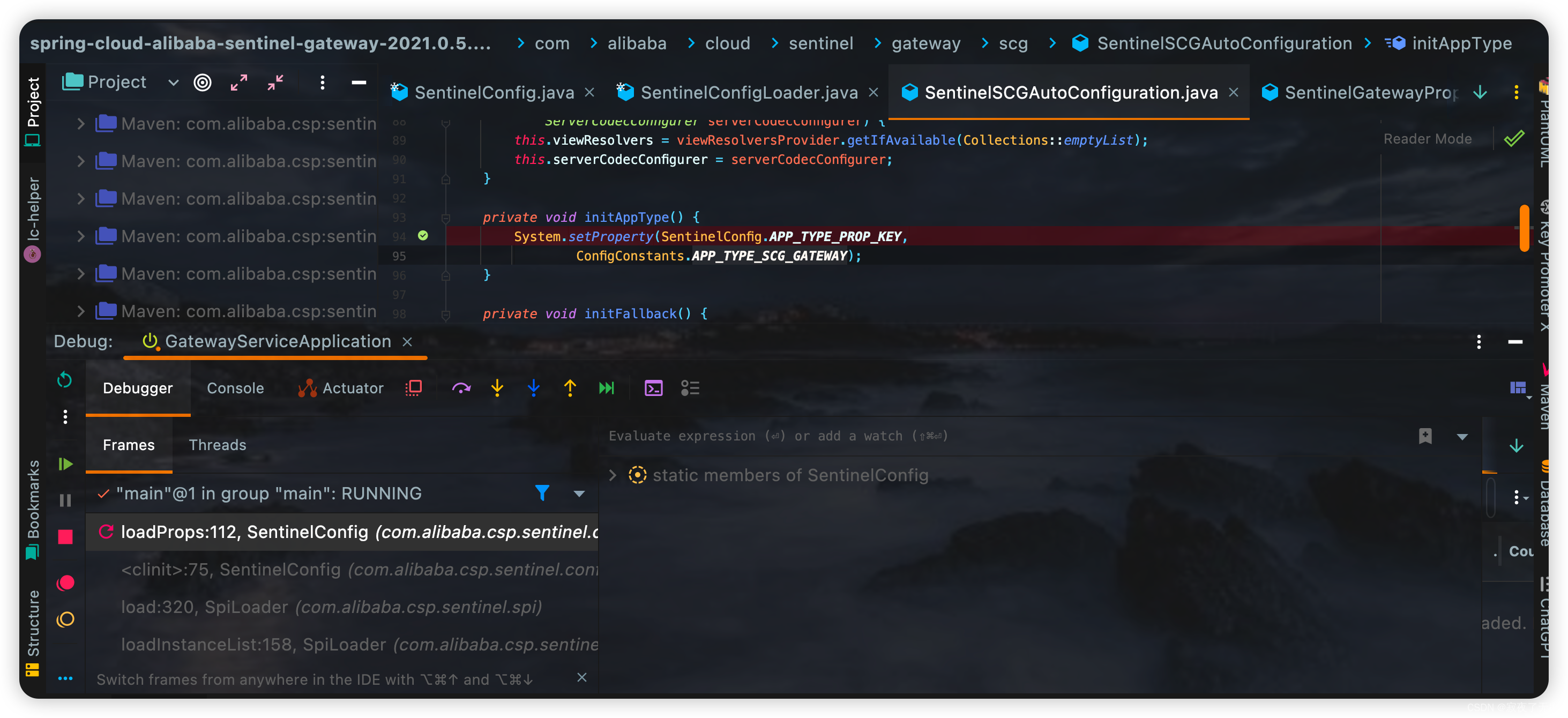
一。问题引入 使用sentinle-dashboard控制台 项目整体升级后,发现控制台上无法看到流控规则了 之前的问题是无法注册上来 现在是注册上来了。结果看不到流控规则配置了。 关于注册不上来的问题,可以看另一篇文章 https://blog.csdn.net/a15835774652/…...

【Spring Boot】社交网站中验证用户登录的checkUser方法
public boolean checkUser(User user) {User userInDb userRepository.findByUsername(user.getUsername());if (userInDb ! null && userInDb.getPassword().equals(user.getPassword())) {return true;} else {return false;}} } 这段代码是UserService类中的checkU…...
edge浏览器进行qq截图过保爆决过程
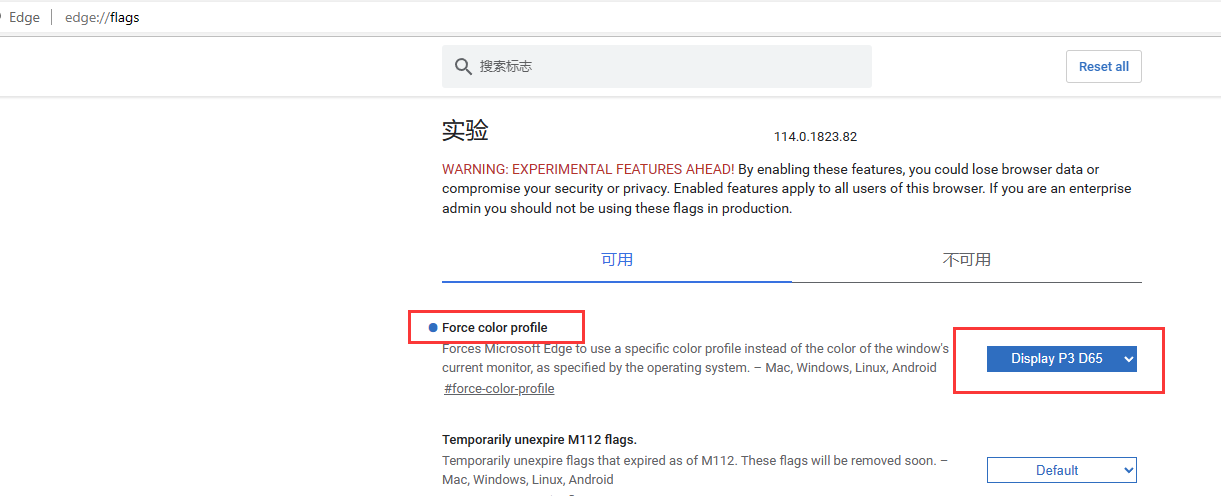
edge浏览器进行qq截图过保解决过程 参考:电脑截屏曝光特别高怎么解决? - 知乎 问题展示 饱和度过高,刺眼 1. 在chrome地址栏输入chrome://flags/ 2. 在页面的搜索栏搜索force color profile 3. 在选项中选择所对应的颜色管理。(…...

【Linux】Linux在防火墙firewall中开放或删除某端口
在生产中往往是不能关闭防火墙firewall的(以下操作是在linux中执行的) #补充一下查看防火墙的命令 #查看防火墙状态 systemctl status firewalld #关闭防火墙 systemctl stop firewalld #重启防火墙 systemctl restart firewalld #启动防火墙 systemctl …...
C++构造函数初始化列表
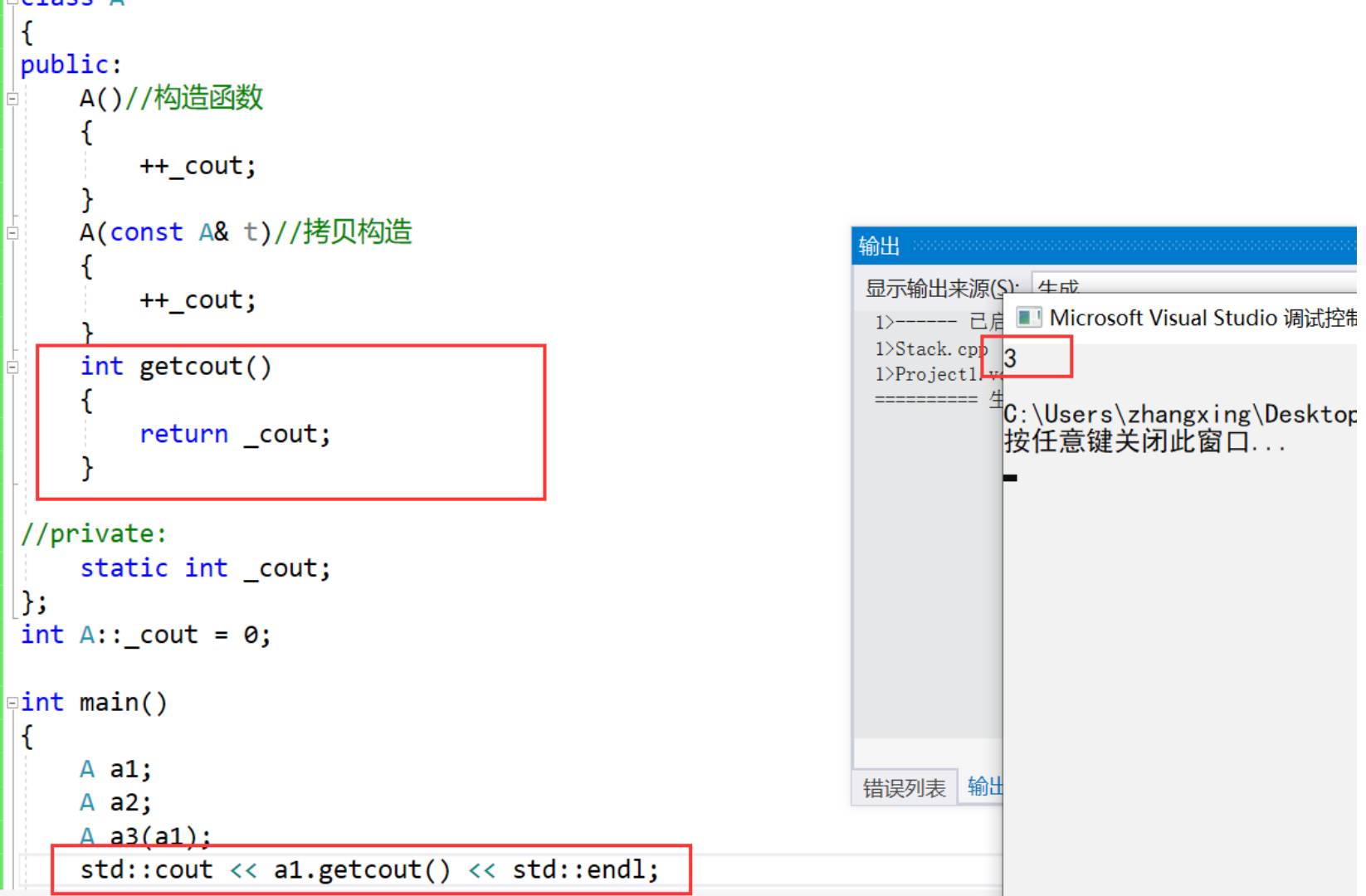
构造函数的一项重要功能是对成员变量进行初始化,为了达到这个目的,可以在构造函数的函数体中对成员变量一一赋值,还可以采用初始化列表。 C构造函数的初始化列表使得代码更加简洁,请看下面的例子: #include <iostre…...

c语言调用mciSendString播放音乐
如下所示,这是一个使用c语言调用系统方法mciSendString(),让系统播放音乐的示例: baihuaxiang 代码: #include <graphics.h> #include <Windows.h> #include <mmsystem.h>#pragma comment(lib,"WINMM.LIB…...

Qt:qRegisterMetaType为Qt信号和槽添加自定义参数类型
背景 qt信号和槽之间的参数传递默认只能传递qt内部已有的类型,例如QString等,若我们自定义类型作为参数时,虽然编译不会报错,但运行时会提示connect无效,无法识别自定义的类。 此时需要我们将自定义类进行注册&#…...

ffmpeg rtp发送video和audio并播放
发送h264 video ffmpeg -re -stream_loop -1 -i h264.mp4 -vcodec h264 -f rtp rtp://127.0.0.1:5006SDP: v0 o- 0 0 IN IP4 127.0.0.1 sNo Name cIN IP4 127.0.0.1 t0 0 atool:libavformat LIBAVFORMAT_VERSION mvideo 5006 RTP/AVP 96 artpmap:96 H264/90000 afmtp:96 packe…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
