弯道超车必做好题集锦二(C语言选择题)
前言:
编程想要学的好,刷题少不了,我们不仅要多刷题,还要刷好题!为此我开启了一个弯道超车必做好题锦集的系列,每篇大约10题左右。此为第二篇选择题篇,该系列会不定期更新,后续还会开编程题的系列。敬请期待!
int main (){char str [] = "Geneius" ;print ( str );return 0 ;}print ( char * s ){if ( * s ){print ( ++ s );printf ( "%c" , * s );}}
A: suiene B: neius C: run-time error D: suieneG
正确答案: A代码实现了递归倒序打印字符串的功能,但是 ++s 使得 s 的值发生了变化,回不到 'G' 的位置上,故而没有打印 'G'
正确答案: D本题主要考虑数组越界访问的情况,二维数组的行和列都是从 0 开始的,对于 a 数组来说,行下标最大是 1 ,列下标最大是 2 ,D选项中 1>2 表达式的值是 0 ,是正确的,其他选项行和列都可能存在越界, A 是行越界, B 是行和列都越界, C 是列越界。
正确答案: Asizeof是C 语言中的一个操作符,不是函数调用,简单的说其作用就是返回一个对象或者类型所占的内存字节数,结果是无符号整数,因此可以把它看作是整型表达式。所以选择A
4.二维数组X按行顺序存储,其中每个元素占1个存储单元。若 X[4][4] 的存储地址为 Oxf8b82140 , X[9][9] 的存储地 址为 Oxf8b8221c ,则 X[7][7] 的存储地址为( )
正确答案: A假设每行有 n个元素:即X[4][4]只需要加上5就可以得到X[4][9]了,而得到的位置和X[9][9]相差5行, 那x[9][9] 元素的地址 - x[4][4] 元素的地址 = 0x21c-0x140=5n+5(21c 和 140 是地址末三位的十六进制 数) ,这里 n 是 43 ,假设 x[7][7] 的地址是 z,x[7][7] 元素的地址 - x[4][4] 元素的地址 = z-0x140 = 3n+3 , z = 3n+3+140 = 3*43+3+0x140 = 0x84+0x140 = 0x1c4,看地址的尾数,选择 A
int func ( int x ){int count = 0 ;while ( x ){count ++ ;x = x & ( x - 1 ); // 与运算}return count ;}
正确答案: Cx=x&(x-1)这个表达式执行一次就会将x的2进制中最右边的1 去掉,在 x 变成 0 之前,表达式能执行几次,就去掉几个 1 ,所以这 个代码实现了求一个有符号整数二进制补码中1 的个数的功能,我们知道 -1 的补码是全 1 ,而 int 类型 4 个字节 32 位,选 C
6.读代码选结果( )
int count = 0 ;int x = - 1 ;while ( x ){count ++ ;x = x >> 1 ;}printf ( "%d" , count );
1. 左移 << : 最左侧位不要了 , 最右侧补 0。
2. 右移 >> : 最右侧位不要了 , 最左侧补符号位 ( 正数补 0, 负数补1)。
3. 无符号右移 >>>: 最右侧位不要了 , 最左侧补 0.(c语言没有,java有)
正确答案: D此题一个关键,有符号数右移运算高位是补符号位的,负数的符号位是 1 ,所以 x 永远不会变为 0 ,是个死循环
7.下述赋值语句错误的是( )
正确答案: CC 选项中 a/b 是表达式,表达式计算的结果是一个值不能做左值
8.以下程序运行后的输出结果是()
int main (){int a = 1 , b = 2 , m = 0 , n = 0 , k ;k = ( n = b < a ) && ( m = a );printf ( "%d,%d\n" , k , m );return 0 ;}
正确答案: Ak=(n=b<a)&&(m=a); 这部分的执行顺序如下:先执行 n=b<a 部分,其中,关系运算符优先级高于赋值运算符,所以先算 b<a ,得到0 , n=0 赋值运算的结果将作为括号内表达式的结果,即 (n=b<a)&&(m=a) 转换成 (0)&&(m=a),&&运算前表达式为假,则后面的括号(m=a)不运算,m值还是0,最后,&&的结果是0,即k=0
9.下面函数的输出结果是( )
int main (){int k = 1 ^ ( 1 << 31 >> 31 );printf ( "%d\n" , k );}
A: 0 B: -1 C: -2 D: 1
正确答案: C(1<<31); 左移 31 位,并在右侧填充 0 ,得到 0x80000000 ,即符号位为 1 ,其他为 0 ,即 -2147483648 int k =1^(1<<31>>31);注意,这里在右移的时候,符号位保持为 1 ,右移后填充 1 ,结果为 0xFFFFFFFF ,即 -1 ,0x00000001^0xFFFFFFFF,即 0xFFFFFFFE(-2)
10.如下代码的输出结果是( )
#include <stdio.h>int main (){int i = 1 ;sizeof ( i ++ );printf ( "%d\n" , i );return 0 ;}
A: 1 B: 4 C: 2 D: 8
正确答案: A一般表达式的运算是在运行时执行的,而 sizeof 是一个编译阶段就执行的运算符,在其内的任何运算都不执行,只推测出其中表达式结果的类型求其大小,故前后i 的值不变。
以上为我个人的小分享,如有问题,欢迎讨论!!!
都看到这了,不如关注一下,给个免费的赞 ![]()

相关文章:

弯道超车必做好题集锦二(C语言选择题)
前言: 编程想要学的好,刷题少不了,我们不仅要多刷题,还要刷好题!为此我开启了一个弯道超车必做好题锦集的系列,每篇大约10题左右。此为第二篇选择题篇,该系列会不定期更新,后续还会…...
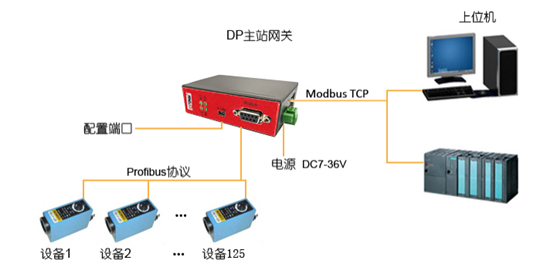
PROFIBUS主站转MODBUS TCP网关
1.产品功能 YC-DPM-TCP网关在Profibus总线侧实现主站功能,在以太网侧实现ModbusTcp服务器功能。可将Profibus DP从站接入到ModbusTcp网络;通过增加DP/PA耦合器,也可将Profibus PA从站接入ModbusTcp网络。YC-DPM-TCP网关最多支持125个Profibu…...
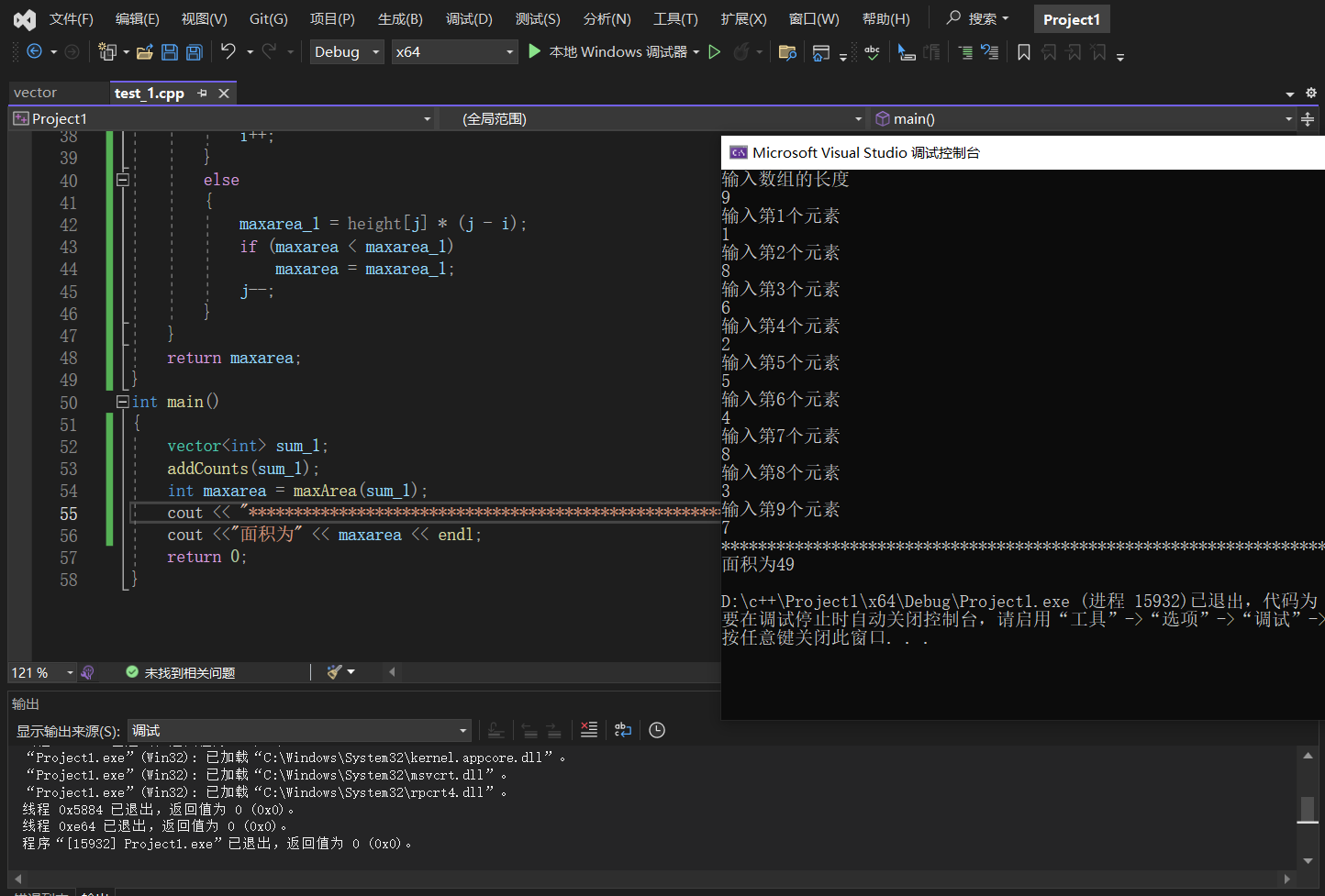
【力扣】盛最多水的容器
目录 题目 题目初步解析 水桶效应 代码实现逻辑 第一步 第二步 第三步 代码具体实现 注意 添加容器元素的函数 计算迭代并且判断面积是否是最大值 总代码 运行结果 总结 题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是…...
【SQL应知应会】索引(三)• MySQL版:聚簇索引与非聚簇索引;查看索引与删除索引;索引方法
欢迎来到爱书不爱输的程序猿的博客, 本博客致力于知识分享,与更多的人进行学习交流 本文收录于SQL应知应会专栏,本专栏主要用于记录对于数据库的一些学习,有基础也有进阶,有MySQL也有Oracle 索引 • MySQL版 前言一、索引1.简介2.索引类型之逻…...
rtmp直播
技术要求:nginxnginx-rtmpffmpegVLC 跟着大佬走的: 传送门 准备工作: 首先需要一台公网ip的服务器 这是使用天翼云的弹性云主机:免费试用1个月 天翼云官网 点击关机,更多里面选择重置密码, 默认用户名为…...

4.14 tcp_tw_reuse 为什么默认是关闭的?
开启 tcp_tw_reuse 参数可以快速复用处于 TIME_WAIT 状态的 TCP 连接时,相当于缩短了 TIME_WAIT 状态的持续时间。 tcp_tw_reuse 是什么? TIME_WAIT 状态的持续时间是 60 秒,这意味着这 60 秒内,客户端一直会占用着这个端口。端…...

Python数据分析和爬虫:解析数据的强大工具
引言: 在当今数据爆炸的时代,数据分析和数据提取变得越来越重要。作为一种简洁而强大的编程语言,Python在数据分析和爬虫领域有着广泛的应用。本文将详细介绍Python在数据分析和爬虫中的常用库和技术,并探讨其在实际应用中的优势…...
)
机器学习之SGD(Stochastic Gradient Descent,随机梯度下降)
SGD(Stochastic Gradient Descent,随机梯度下降)是深度学习中最基本的优化算法之一。它是一种迭代式的优化方法,用于训练神经网络和其他机器学习模型。以下是关于SGD优化器的重要信息: 基本原理:SGD的基本思…...

leetcode做题笔记100. 相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。 思路一: bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p NULL &…...

【Hadoop】Hadoop入门概念简介
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_Linux,Java基础学习,大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的…...
)
前端监控之异常监控(一)
前言 当我们的项目中假设出现了下面几种场景: 点击按钮后,页面无响应页面跳转后显示白屏页面卡顿...... 这些情况都是非常影响用户体验的,对于用户来说,是难以接受的,用户可能就此流失掉了。 因此前端非常有必要针对…...

sql server 、mysql CTE 公用表表达式
sql server 详细 mysql CTE CTE 是一个命名的临时结果集,作用范围是当前语句。CTE可以理解成一个可以复用的子查询,当然跟子查询还是有点区别的,CTE可以引用其他CTE,但子查询不能引用其它子查询。所以,开发中建议…...

Oracle dataguard 和Oracle rac的区别和联系
RAC服务器共用一套存储,同时提供服务,没有主备之分.宕一个其它的可以继续服务. 双机热备,共用一套存储,一个提供服务一个备份,主机宕了切换到备份服务器提供服务. data guard 完全两套系统,存储是单独的,用日志同步. RAC: 实例层冗余 DG :数据库层冗…...

JUC工具类-LockSupport概述
前言 多线程并发场景中,时常需要线程协同,故而需要对当前线程进行阻塞,并唤醒需要协同的线程来一起完成任务。 通常处理方式有三种: 1)Synchronized加锁的线程 使用Object类下所提供的方法: wai…...

大数据:AI大模型对数据分析领域的颠覆(文末送书)
随着数字化时代的到来,大数据已经成为了各行各业中不可或缺的资源。然而,有效地分析和利用大数据仍然是一个挑战。在这个背景下,OpenAI推出的Code Interpreter正在对数据分析领域进行颠覆性的影响。 如何颠覆数据分析领域?带着这…...
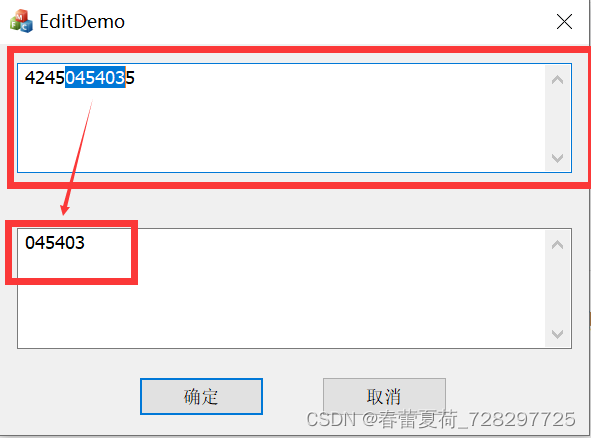
CEdit 选中文字实时更新到另一个控件中
有时候,我们会遇到需求,软件中需要让选中一个CEdit控件中的文字实时更新到另一个控件中,实现效果如下所示: 代码如下: BOOL CEditDemoDlg::PreTranslateMessage(MSG* pMsg) { CEdit* pOldEdit (CEdit*)GetDlgIte…...

Word导出创建Adobe PDF其中emf图片公式马赛克化及文字缺失
软件版本 Word 2021 Visio 2019 Adobe Acrobat Pro 2020 问题描述 公式马赛克化,是指在Word中使用MathType编辑的公式,然后在Visio中使用图片(增强型图元文件)形式得到的粘贴对象,效果如下 文字缺失,是指Word导出→创建Adobe P…...
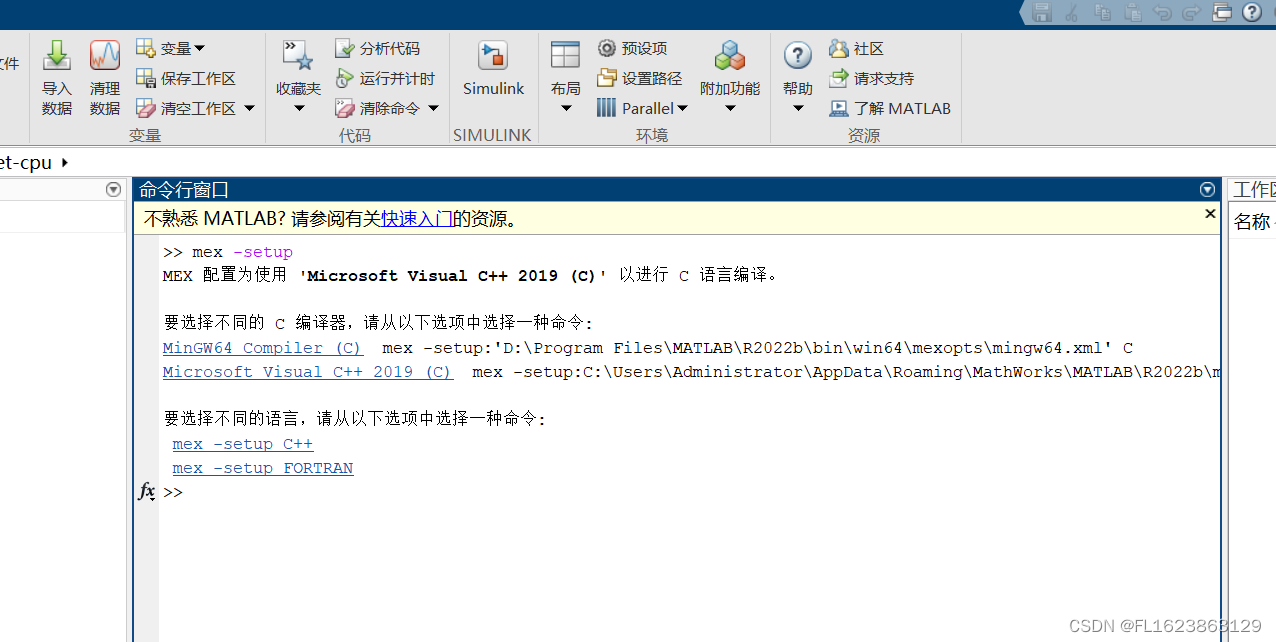
[matlab]matlab配置mingw64编译器
第一步:下载官方绿色版本mingw64编译器然后解压放到一个非中文空格路径下面 比如我mingw64-win是我随便改的文件名,然后添加环境变量,选择用户或者系统环境变量添加下面的变量 变量名: MW_MINGW64_LOC 变量值:自己的m…...

华为OD-非严格递增连续数字序列
题目描述 输入一个字符串仅包含大小写字母和数字 求字符串中包含的最长的非严格递增连续数字序列长度 比如: 12234属于非严格递增数字序列 输入描述 输入一个字符串仅包含大小写字母和数字 输出描述 输出字符串中包含的最长的非严格递增连续数字序列长度 示例…...
css滚动条样式这样修改下很漂亮
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>滚动条样式修改下很漂亮(不支持IE)</title> <style type"text/css"> * { margin: 0; padding: 0; } .box { width: 300px; height: 100px; margin…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
