P1052 [NOIP2005 提高组] 过河
[P1052 NOIP2005 提高组] 过河 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
问题描述:给定长度L,和一次可以跳动的长度 s 到 t,给定m个石头的位置,求最少经过多少个石头可以超过L。
思路:如果L很小的话,就是简单dp。
i f i 有石头 F ( i ) = m i n ( F ( i ) , F ( i − j ) + 1 ) j ∈ [ s , t ] e l s e F ( i ) = m i n ( F ( i ) , F ( i − j ) ) j ∈ [ s , t ] if \quad i有石头 \quad F(i) = min(F(i), F(i - j) + 1) \quad j \in [s,t] \\ else \quad F(i) = min(F(i), F(i-j)) \quad j \in [s,t] ifi有石头F(i)=min(F(i),F(i−j)+1)j∈[s,t]elseF(i)=min(F(i),F(i−j))j∈[s,t]
但是发现,L特别大,但是石头个数却特别小,同时也发现s和t也很小,就算m * t * s最大也才1000。如果将石头距离进行缩小就可以过。
对于 两个石头距离大于s * t的来说,对于区间[s * t, 两个石头之间的距离]都是可以经过跳[s, t]这些个数给到达的。因此,可以将两个石头距离大于s * t的缩小为s * t,这样就可以用上面的状态转移方程。
缩点
int st = s * t;rep(i,1,m) {int dist = a[i] - a[i-1];if(dist >= st) dist = st;ph[i] = ph[i-1] + dist;// 将石头所在的那个点进行赋值为 truevis[ph[i]] = 1;}
状态转移方程
int len = ph[m] + st; memset(f, 0x3f, sizeof(f));f[0] = 0;rep(i,1,len) {rep(j,s,t) {if(i - j >= 0) {if(vis[i]) f[i] = min(f[i-j] + 1, f[i]);else f[i] = min(f[i-j], f[i]);}}}
求答案
int ans = INF;rep(i,ph[m],len) {ans = min(ans, f[i]);}
对s == t进行特判
if(s == t) { // 特判 s == tint cnt = 0;rep(i,1,m) if(a[i] % s == 0) cnt++;cout<<cnt;return ;}
AC代码
const int N = 2e5 + 21;
int a[N], f[N],ph[N];
bool vis[N];
void solve() {int L,s,t,m; cin>>L>>s>>t>>m;rep(i,1,m) cin>>a[i];// 需要进行排序,石头位置初始是无序的sort(a+1, a+m+1);if(s == t) { // 特判 s == tint cnt = 0;rep(i,1,m) if(a[i] % s == 0) cnt++;cout<<cnt;return ;}// 如果 两个石头之间的距离大于等于 s * t,进行缩点/*** 因为,假设 两个石头距离为 len* 如果 len > s * t,则在 [s*t, len] 这个区间内的每一个点都可以访问到*/int st = s * t;rep(i,1,m) {int dist = a[i] - a[i-1];if(dist >= st) dist = st;ph[i] = ph[i-1] + dist;// 将石头所在的那个点进行赋值为 truevis[ph[i]] = 1;}// 因为是大于L就行,因此可能有超过L,但是是最小次数的情况int len = ph[m] + st; memset(f, 0x3f, sizeof(f));f[0] = 0;rep(i,1,len) {rep(j,s,t) {if(i - j >= 0) {if(vis[i]) f[i] = min(f[i-j] + 1, f[i]);else f[i] = min(f[i-j], f[i]);}}}int ans = INF;rep(i,ph[m],len) {ans = min(ans, f[i]);}cout<<ans;
}
相关文章:

P1052 [NOIP2005 提高组] 过河
[P1052 NOIP2005 提高组] 过河 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 问题描述:给定长度L,和一次可以跳动的长度 s 到 t,给定m个石头的位置,求最少经过多少个石头可以超过L。 思路:如果L很小的话࿰…...

ArrayList和Vector及LinkedList的区别
1.ArrayList和Vector的区别 第一句话:ArrayList和Vector底层都是数组实现的,初始容量都为10;在ArrayList的底层,是通过定义一个DEFAULT_CAPACITY的常量来指定的,而Vector的底层,是直接在空参构造中&#x…...

HVV爆火漏洞:最新 WPS RCE (远程命令执行) 复现
最近HVV爆出的很火的WPS命令执行漏洞,其实并不是0DAY,早在2019年就出现了,只不过最近EXP才公开。接下来我们来复现一遍。 0x00 影响版本 WPS Office 2023 个人版 < 11.1.0.15120WPS Office 2019 企业版 < 11.8.2.12085 0x01 环境配置…...
我的128天创作纪念日-东离与糖宝
文章目录 机缘收获日常成就憧憬 不知不觉我也迎来了自己的128天创作纪念日,一起来看看我有什么想对大家说的吧 机缘 我的写博客之旅始于参加了代码随想录算法训练营。在训练营期间,代码随想录作者卡尔建议我们坚持每天写博客记录刷题学习的进度和心得体…...

卷积神经网络——下篇【深度学习】【PyTorch】【d2l】
文章目录 5、卷积神经网络5.10、⭐批量归一化5.10.1、理论部分5.10.2、代码部分 5.11、⭐残差网络(ResNet)5.11.1、理论部分5.11.2、代码部分 话题闲谈 5、卷积神经网络 5.10、⭐批量归一化 5.10.1、理论部分 批量归一化可以解决深层网络中梯度消失和…...

cas md5加密
CAS Authentication Credentials #cas.authn.accept.userscasuser::Mellon 查询账号密码SQL,必须包含密码字段 cas.authn.jdbc.query[0].sqlselect * from ca_user where username? 指定上面的SQL查询字段名(必须) cas.authn.jdbc.query…...

[管理与领导-51]:IT基层管理者 - 8项核心技能 - 6 - 流程
前言: 管理者存在的价值就是制定目标,即目标管理、通过团队(他人)拿到结果。 要想通过他人拿到结果: (1)目标:制定符合SMART原则的符合业务需求的目标,团队跳一跳就可以…...

天翼物联、汕头电信与汕头大学共建新一代信息技术与数字创新(物联网)联合实验室
近日,在工业和信息化部和广东省人民政府共同主办的2023中国数字经济创新发展大会上,天翼物联、汕头电信与汕头大学共建“新一代信息技术与数字创新(物联网)”联合实验室签约仪式举行。汕头大学校长郝志峰、中国电信广东公司总经理…...
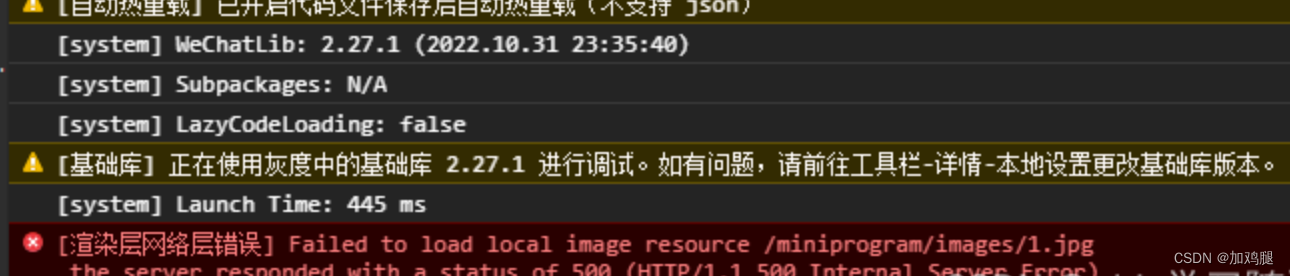
Failed to load local image resource/images/1.jpg无法加载本地图片资源
微信小程序开发无法加载本地图片 先放报错图片 绝对路径不行, <image src"../../images/1.jpg" mode"heightFix"></image>使用相对路径就可以了 <image src"../../images/1.jpg" mode"heightFix"><…...

Go和Java实现责任链模式
Go和Java实现责任链模式 下面通过一个审批流程的案例来说明责任链模式的使用。 1、责任链模式 责任链模式为请求创建了一个接收者对象的链。这种模式给予请求的类型,对请求的发送者和接收者进行解耦。这 种类型的设计模式属于行为型模式。 在这种模式中&#x…...

C#+GDAL影像处理笔记08:生成DEM的图阔范围线
目录 1 实现思路 2 源码及解析 1 实现思路 首先获取DEM数据的转换参数信息,这个信息记录了DEM的放射变换参数,包括左上角X,X方向分辨率、0、左上角Y、0、Y方向的分辨率【负值】等信息。接着是根据转换参数,计算DEM分幅数据的四至范围坐标;主要用到上一步得到的转换参数信…...
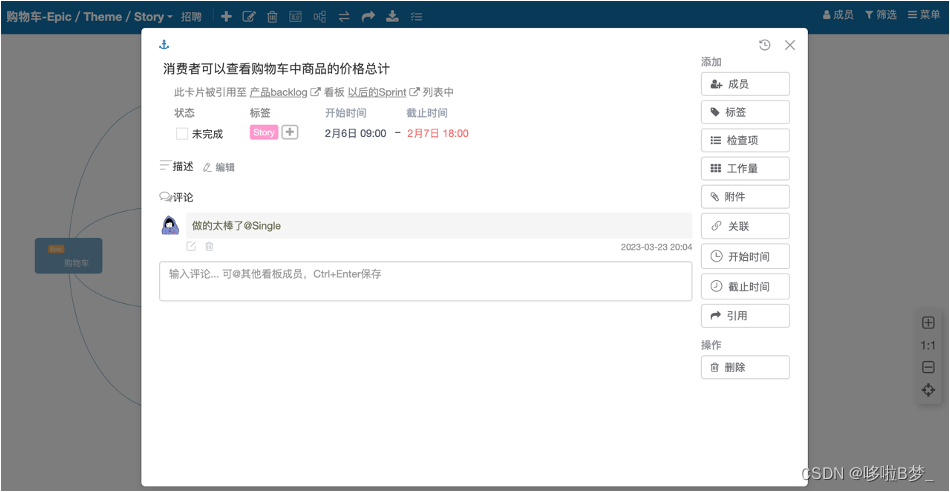
敏捷研发管理软件及敏捷管理流程
Scrum中非常强调公开、透明、直接有效的沟通,这也是“可视化的管理工具”在敏捷开发中如此重要的原因之一。通过“可视化的管理工具”让所有人直观的看到需求,故事,任务之间的流转状态,可以使团队成员更加快速适应敏捷开发流程。 …...
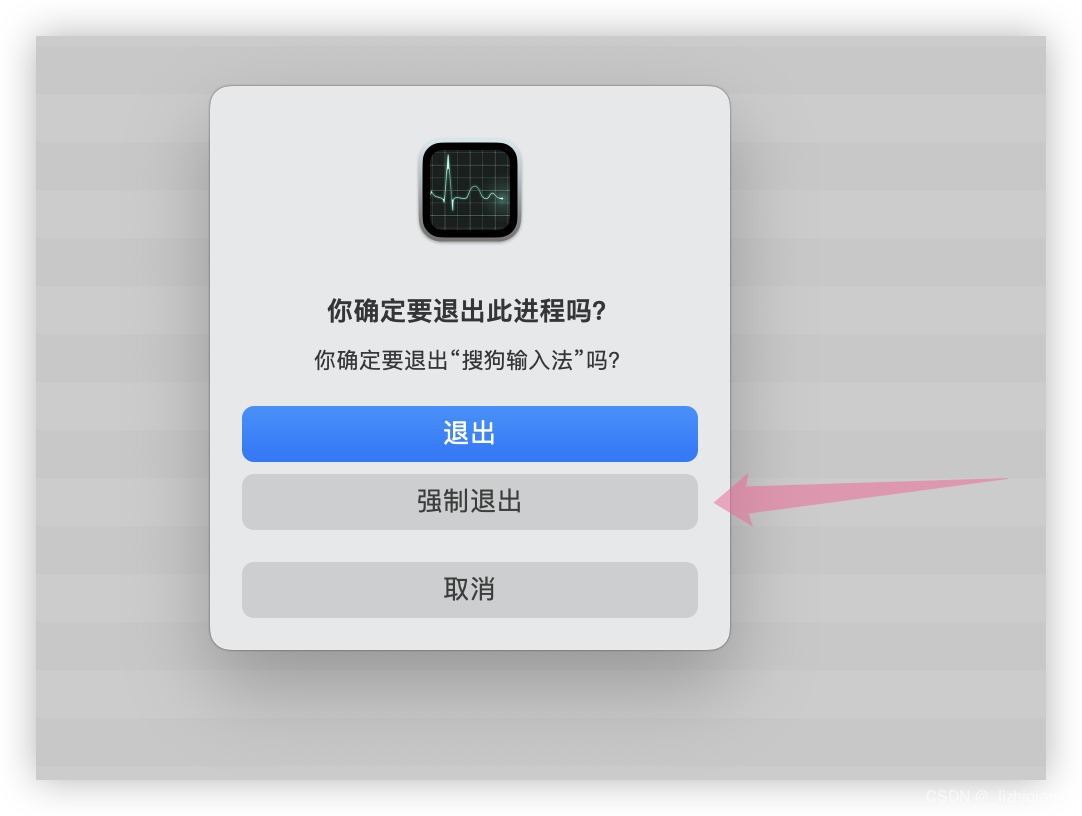
Mac OS 13.4.1 搜狗输入法导致的卡顿问题
一、Mac OS 系统版本 搜狗输入法已经更新到最新 二、解决方案 解决方案一 在我的电脑上面需要关闭 VSCode 和 Chrmoe 以后,搜狗输入法回复正常。 解决方案二 强制重启一下搜狗输入法。 可以用 unix 定时任务去隔 2个小时自动 kill 掉一次进程 # kill 掉 mac …...
vue 简单实验 自定义组件 局部注册
1.概要 2.代码 <html> </html> <script src"https://unpkg.com/vuenext" rel"external nofollow" ></script> <body><div id"counter"><component-a></component-a></div> </body&g…...
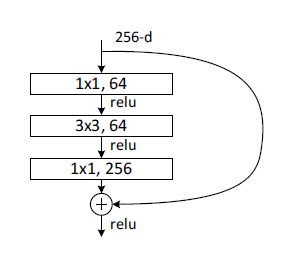
Resnet模型详解
1、Resnet是什么? Resnet是一种深度神经网络架构,被广泛用于计算机视觉任务,特别是图像分类。它是由微软研究院的研究员于2015年提出的,是深度学习领域的重要里程碑之一。 2、网络退化问题 理论上来讲,随着网络的层…...

AI 绘画Stable Diffusion 研究(十六)SD Hypernetwork详解
大家好,我是风雨无阻。 本期内容: 什么是 Hypernetwork?Hypernetwork 与其他模型的区别?Hypernetwork 原理Hypernetwork 如何下载安装?Hypernetwork 如何使用? 在上一篇文章中,我们详细介绍了 …...
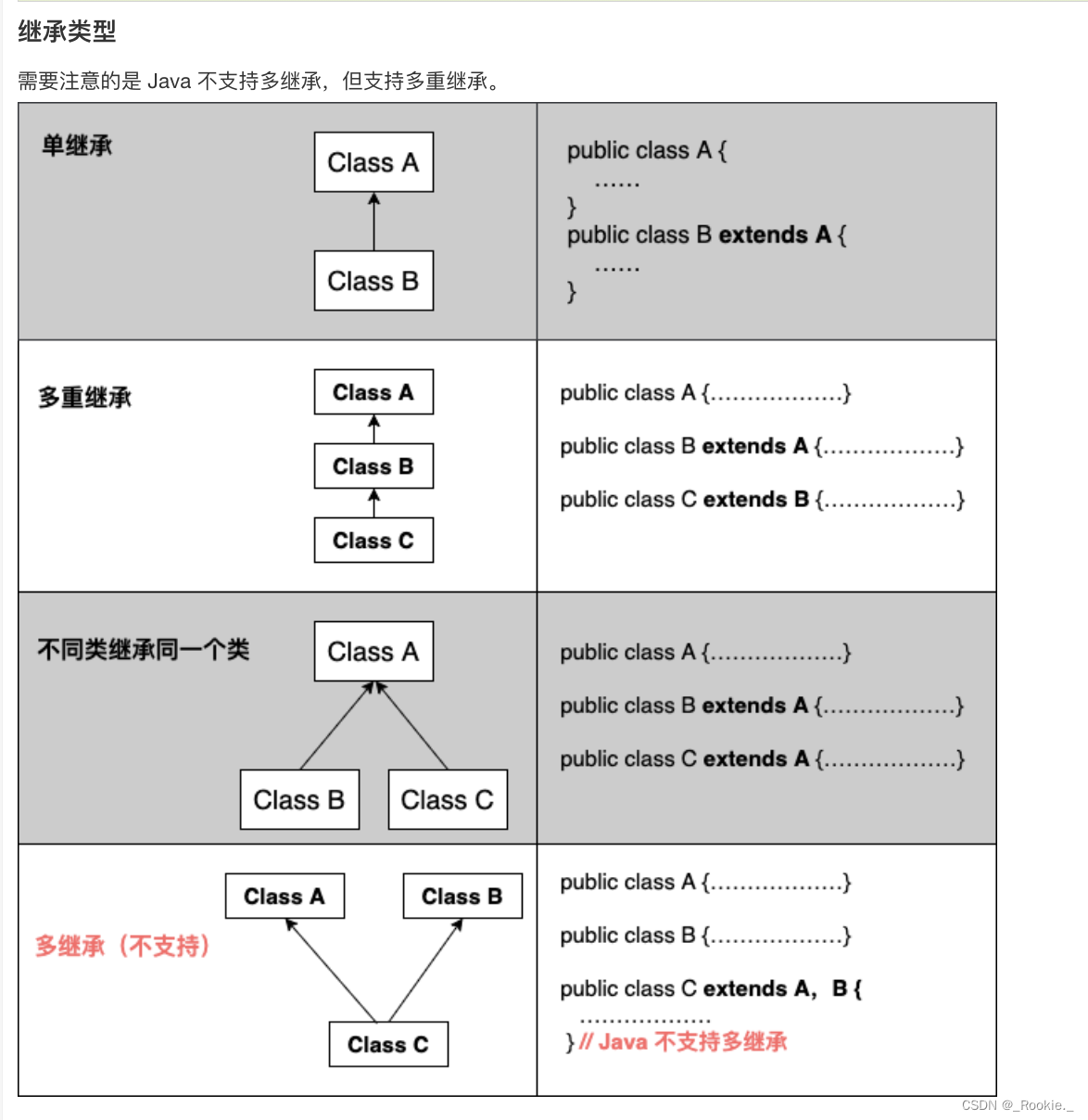
2023.8 -java - 继承
继承就是子类继承父类的特征和行为,使得子类对象(实例)具有父类的实例域和方法,或子类从父类继承方法,使得子类具有父类相同的行为。 继承的特性 子类拥有父类非 private 的属性、方法。 子类可以拥有自己的属性和方法…...

前端面试:【移动端开发】PWA、Hybrid App和Native App的比较
在移动端开发中,开发者有多种选择,包括渐进式Web应用(PWA),混合应用(Hybrid App)和原生应用(Native App)。每种方法都有其独特的优势和适用场景。本文将对它们进行比较&a…...
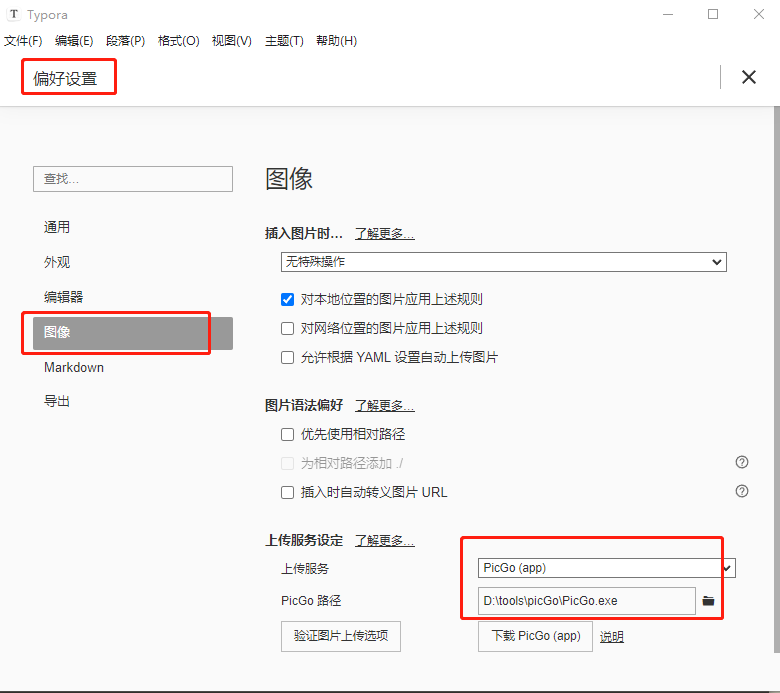
picGo+gitee+typora设置图床
picGogiteetypora设置图床 picGogitee设置图床下载picGo软件安装picGo软件gitee操作在gitee中创建仓库在gitee中配置私人令牌 配置picGo在插件设置中搜索gitee插件并进行下载 TyporapicGo设置Typora 下载Typora进行图像设置 picGogitee设置图床 当我了解picGogitee可以设置图床…...
[JavaWeb]【十三】web后端开发-原理篇
目录 一、SpringBoot配置优先级 1.1 配置优先级比较 1.2 java系统属性和命令行参数 1.3 打包运行jar 1.4 综合优先级编辑 二、Bean管理 2.1 获取bean 2.2 bean作用域 2.2.1 五种作用域 2.2.2 配置作用域 2.3 第三方bean 2.3.1 编写公共配置类 三、SpringBoot原理 …...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
