Fortran 微分方程求解 --ODEPACK
最近涉及到使用Fortran对微分方程求解,我们知道MATLAB已有内置的函数,比如ode家族,ode15s,对应着不同的求解办法。通过查看odepack的官方文档,我尝试使用了dlsode求解刚性和非刚性常微分方程组。
首先是github网址:https://github.com/jacobwilliams/odepack
具体使用办法:
1.我使用的是vs2022,比较简单的用法就是把,src文件夹所有的文件复制到和项目一个文件夹即可,将M_odepack.f90文件放入到项目中,这样就可以用了。
2.在使用前要use m_odepack
3.这里以官方文档中的例子为例:
program dlsode_ex
use m_odepack
implicit none
external fex
external jexinteger,parameter :: dp=kind(0.0d0)
real(kind=dp),dimension(3) :: atol,y
integer :: iopt,iout,istate,itask,itol,liw,lrw,mf,neq
integer,dimension(23) :: iwork
real(kind=dp) :: rtol,t,tout
real(kind=dp),dimension(58) :: rworkneq = 3y(1) = 1.D0y(2) = 0.D0y(3) = 0.D0t = 0.D0tout = .4D0itol = 2rtol = 1.D-4atol(1) = 1.D-6atol(2) = 1.D-10atol(3) = 1.D-6itask = 1istate = 1iopt = 0lrw = 58liw = 23mf = 21do iout = 1,12call dlsode(fex,[neq],y,t,tout,itol,[rtol],atol,itask,istate,iopt, && rwork,lrw,iwork,liw,jex,mf)write (6,99010) t,y(1),y(2),y(3)99010 format (' At t =',d12.4,' y =',3D14.6)if ( istate<0 ) thenwrite (6,99020) istate99020 format (///' Error halt.. ISTATE =',i3)stop 1elsetout = tout*10.D0endifenddowrite (6,99030) iwork(11),iwork(12),iwork(13)99030 format (/' No. steps =',i4,', No. f-s =',i4,', No. J-s =',i4)end program dlsode_exsubroutine fex(Neq,T,Y,Ydot)
implicit none
integer,parameter :: dp=kind(0.0d0)integer :: Neq
real(kind=dp) :: T
real(kind=dp),intent(in),dimension(3) :: Y
real(kind=dp),intent(inout),dimension(3) :: YdotYdot(1) = -.04D0*Y(1) + 1.D4*Y(2)*Y(3)Ydot(3) = 3.D7*Y(2)*Y(2)Ydot(2) = -Ydot(1) - Ydot(3)
end subroutine fexsubroutine jex(Neq,T,Y,Ml,Mu,Pd,Nrpd)
implicit noneinteger,parameter :: dp=kind(0.0d0)
integer :: Neq
real(kind=dp) :: T
real(kind=dp),intent(in),dimension(3) :: Y
integer :: Ml
integer :: Mu
real(kind=dp),intent(inout),dimension(Nrpd,3) :: Pd
integer,intent(in) :: NrpdPd(1,1) = -.04D0Pd(1,2) = 1.D4*Y(3)Pd(1,3) = 1.D4*Y(2)Pd(2,1) = .04D0Pd(2,3) = -Pd(1,3)Pd(3,2) = 6.D7*Y(2)Pd(2,2) = -Pd(1,2) - Pd(3,2)
end subroutine jex一些变量意义具体看文档说明:https://jacobwilliams.github.io/odepack/proc/dlsode.html
其中,假设n是方程个数,
y:是初值,数组,y(n)
atol:每个方程的绝对误差,数组,atol(n)
t:输入的初始点,tout是下一个点。
mf:是求解方法,其中如果等于21,24需要使用者自己提供雅各比矩阵,如示例代码中jex函数中那样,如果等于10,22,25则不需要自己写,但是jex函数还是需要定义,就是函数框架,函数名,变量声明就可。
fex函数:写的就是你的微分方程组
另外,

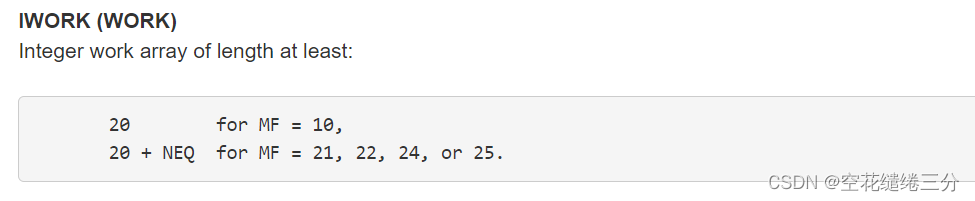
rwork,iwork也是两个一维数组,大小如图所示。
以及,
lrw = 22 + 9*NEQ + NEQ**2
liw = 20 + NEQ
整体使用的逻辑就是先设置t值,然后设置循环,tout不断累加,下次循环就使用上次计算得到的新y值以及tout进行迭代计算。
istate是用于输入和输出以指定计算状态的索引,要注意的是如果istate选择2,或3需要在第一次循环中等于1,初始化,到了第二次循环开始才赋值为2或3。
相关文章:

Fortran 微分方程求解 --ODEPACK
最近涉及到使用Fortran对微分方程求解,我们知道MATLAB已有内置的函数,比如ode家族,ode15s,对应着不同的求解办法。通过查看odepack的官方文档,我尝试使用了dlsode求解刚性和非刚性常微分方程组。 首先是github网址&am…...
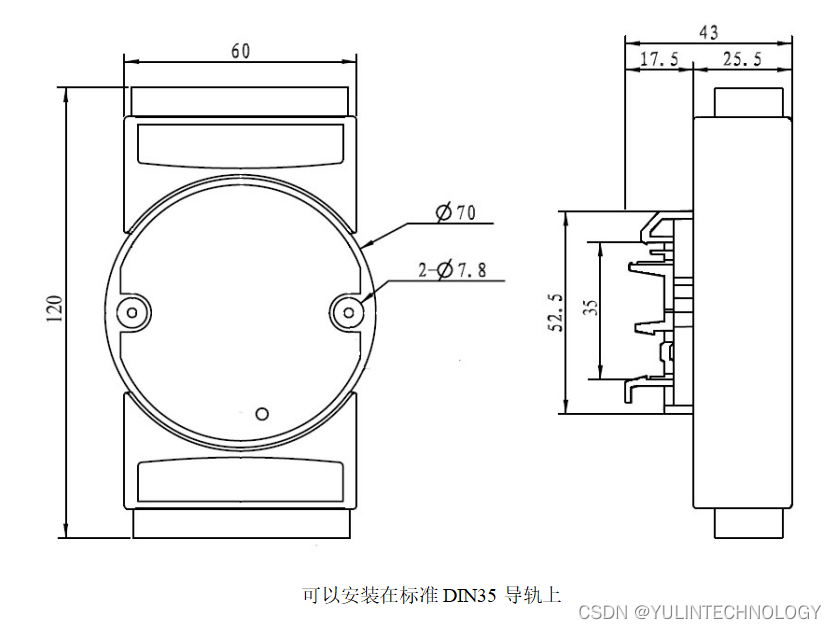
8路光栅尺磁栅尺编码器或16路高速DI脉冲信号转Modbus TCP网络模块 YL99-RJ45
特点: ● 光栅尺磁栅尺解码转换成标准Modbus TCP协议 ● 高速光栅尺磁栅尺4倍频计数,频率可达5MHz ● 模块可以输出5V的电源给光栅尺或传感器供电 ● 支持8个光栅尺同时计数,可识别正反转 ● 可以设置作为16路独立DI高速计数器 ● 可网…...

【Python】函数
None类型 思考:若函数没有使用return语句返回数据,那么函数有返回值吗? 答:实际上是有的,Python中有一个特殊的字面量None,其类型是<class ‘NoneType’>,无返回值的函数,实…...
centos安装MySQL 解压版完整教程(按步骤傻瓜式安装
一、卸载系统自带的 Mariadb 查看: rpm -qa|grep mariadb 卸载: rpm -e --nodeps mariadb-libs-5.5.68-1.el7.x86_64 二、卸载 etc 目录下的 my.cnf 文件 rm -rf /etc/my.cnf 三、检查MySQL是否存在 有则先删除 #卸载mysql服务以及删除所有mysql目录 #没…...
【后端速成 Vue】第一个 Vue 程序
1、为什么要学习 Vue? 为什么使用 Vue? 回想之前,前后端交互的时候,前端收到后端响应的数据,接着将数据渲染到页面上,之前使用的是 JavaScript 或者 基于 JavaScript 的 Jquery,但是这两个用起来还是不太…...

Macbook pro M1 安装Ubuntu教程
先讲下心路历程 由于版主最近刚切换到Mac,所以在安装的时候一上手就选择了virutalbox,结果报错“The installer has detected an unsupported architecture. VirtualBox only runs on the amd64 architecture.” 后来去Reddit论坛上一看,才知…...
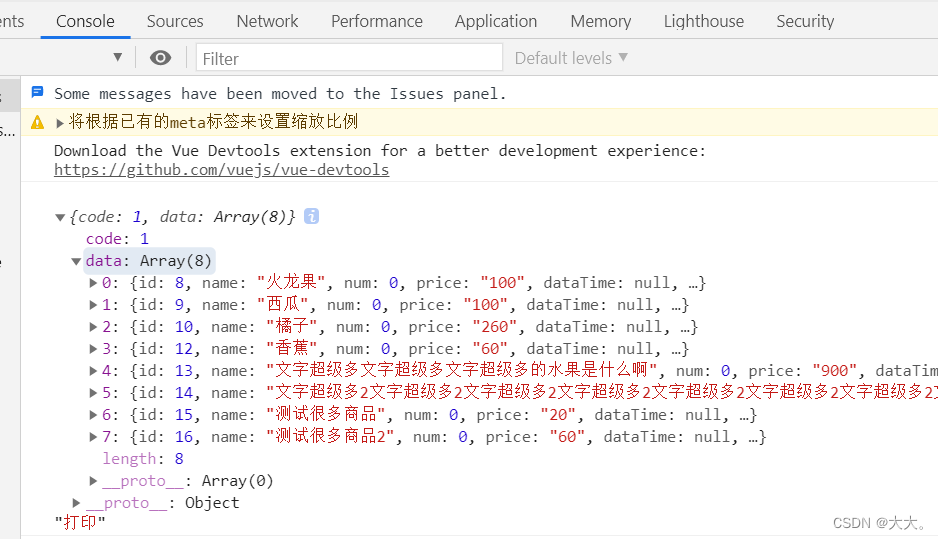
前端console.log打印内容与后端请求返回数据不一致
后端传值num0 前端打印num1 ,如图,console.log后台显示的数据与展开后不一致 造成该问题原因是深拷贝与浅拷贝的问题。 var obj JSON.parse(JSON.stringify(res)) 修改后打印 正常...

SQL入门:多表查询
SQL,或者说结构化查询语言(Structured Query Language),是用于管理和操作关系型数据库的标准语言。在本篇文章中,我们将重点介绍SQL中的多表查询,这是一种强大的工具,可以帮助我们从多个相关的表格中获取数据。 数据库…...
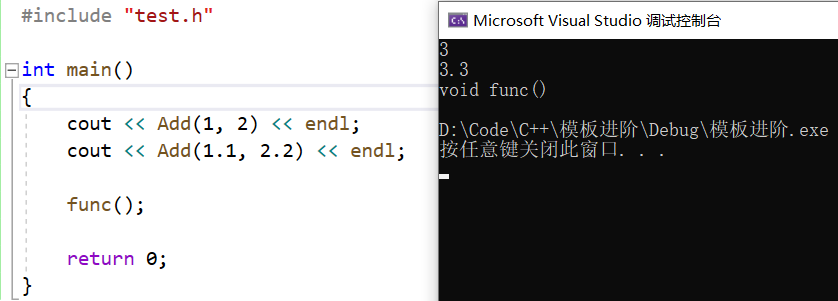
【C++】进一步认识模板
🏖️作者:malloc不出对象 ⛺专栏:C的学习之路 👦个人简介:一名双非本科院校大二在读的科班编程菜鸟,努力编程只为赶上各位大佬的步伐🙈🙈 目录 前言一、非类型模板参数二、模板的特…...

Mysql Oracle 区别
1. oracle select *, id需要在星号前加别名,mysql则不需要 mysql语法: select *, id from xin_student_t;oracle语法: select st.*, st.id from xin_student_t st;2. oracle表定义了别名,在查询时可以不用别名指定字段…...
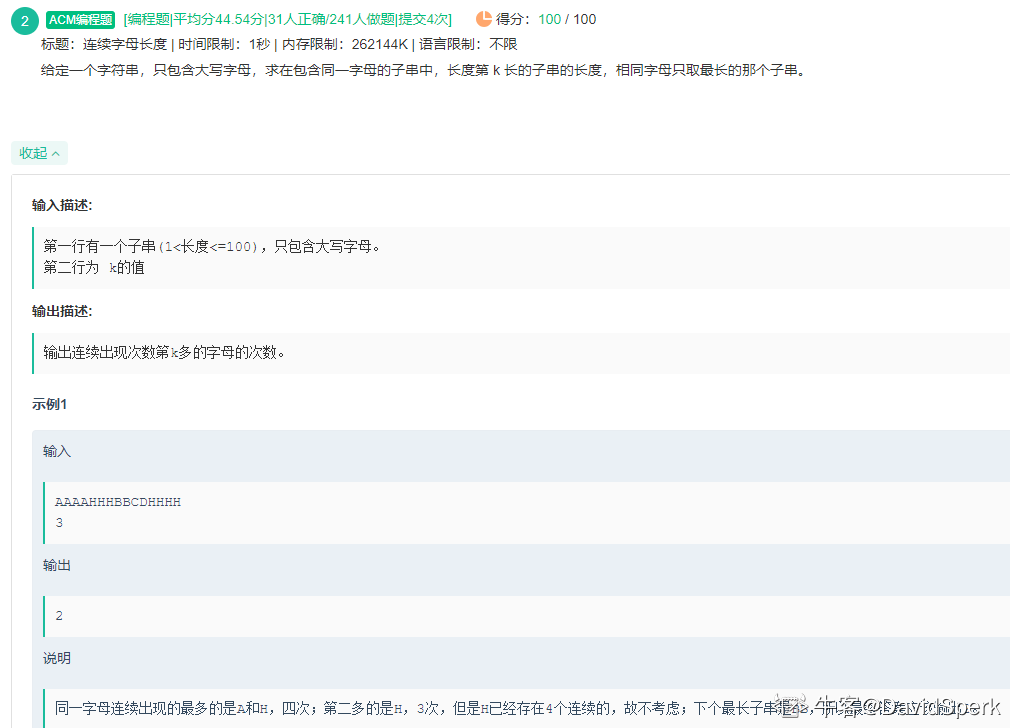
华为OD-第K长的连续字母字符串长度
题目描述 给定一个字符串,只包含大写字母,求在包含同一字母的子串中,长度第 k 长的子串的长度,相同字母只取最长的那个子串。 代码实现 # coding:utf-8 # 第K长的连续字母字符串长度 # https://www.nowcoder.com/discuss/353150…...

【编程题】有效三角形的个数
文章目录 一、题目二、算法讲解三、题目链接四、补充 一、题目 给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。 示例1: 输入: nums [2,2,3,4] 输出: 3 **解释:**有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 …...

【mysql是怎样运行的】-EXPLAIN详解
文章目录 1.基本语法2. EXPLAIN各列作用1. table2. id3. select_type4. partitions5. type 1.基本语法 EXPLAIN SELECT select_options #或者 DESCRIBE SELECT select_optionsEXPLAIN 语句输出的各个列的作用如下: 列名描述id在一个大的查询语句中每个SELECT关键…...

数据结构例题代码及其讲解-链表
链表 单链表的结构体定义及其初始化。 typedef struct LNode {int data;struct LNode* next; }LNode, *LinkList;①强调结点 LNode *p; ②强调链表 LinkList p; //初始化 LNode* initList() {//定义头结点LNode* L (LNode*)malloc(sizeof(LNode));L->next NULL;return …...
[Open-source tool] 可搭配PHP和SQL的表單開源工具_Form tools(1):簡介和建置
Form tools是一套可搭配PHP和SQL的表單開源工具,可讓開發者靈活運用,同時其有數個表單模板和應用模組供挑選,方便且彈性。Form tools已開發超過20年,為不同領域的需求者或開發者提供一個自由和開放的平台,使他們可建構…...

移动数据业务价值链的整合
3G 时代移动数据业务开发体系的建立和发展,要求运营商从封闭、统一的业 务形态、单一提供业务,向开放的、个性化多元化的业务体系以及多方合作参与提 供业务的方向发展,不可避免的使通信价值链不断延长和升级,内容提供商、服务 …...
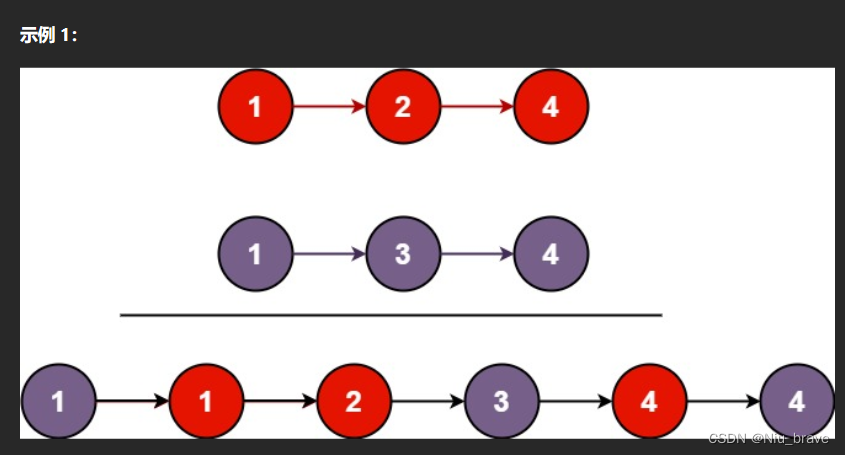
合并两个链表
题目描述 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 比如以下例子: 题目接口: /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListN…...
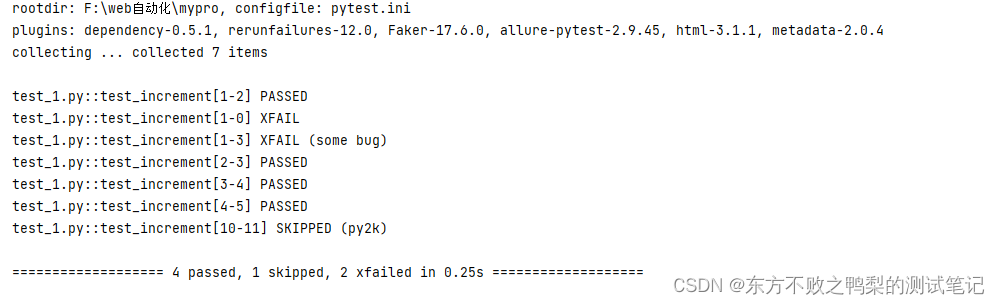
测试框架pytest教程(9)跳过测试skip和xfail
skip无条件跳过 使用装饰器 pytest.mark.skip(reason"no way of currently testing this") def test_example(faker):print("nihao")print(faker.words()) 方法内部调用 满足条件时跳过 def test_example():a1if a>0:pytest.skip("unsupported …...

HTML <textarea> 标签
实例 <textarea rows="3" cols="20"> 收拾收拾 </textarea>定义和用法 <textarea> 标签定义多行的文本输入控件。 文本区中可容纳无限数量的文本,其中的文本的默认字体是等宽字体(通常是 Courier)。 可以通过 cols 和 rows 属性来…...

探索图结构:从基础到算法应用
文章目录 理解图的基本概念学习图的遍历算法学习最短路径算法案例分析:使用 Dijkstra 算法找出最短路径结论 🎉欢迎来到数据结构学习专栏~探索图结构:从基础到算法应用 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:I…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
