Xamarin.Android中的Fragment
目录
- 1、Activity中使用Fragment
- 2、Fragment与Activity通信
- 3、Fragment与其他的Fragment通信
1、Activity中使用Fragment
一般而言,会在activity中添加一个加载fragment的方法。通过点击菜单的按钮,加载不同的fragment。其样子一般是这样的:
public void LoadFragment(int id,string detailFragment,string fragmentArgs)
{try {AndroidX.Fragment.App.Fragment fragment = null;switch (id){case Resource.Id.menu_workspace:fragment = WorkspaceMainFragment.NewInstance(id);//传入某个/些参数break;case Resource.Id.menu_hospital:fragment = HospitalFragment.NewInstance();break;case Resource.Id.menu_mine:fragment = LoginFragment.NewInstance();break;default:break;}if (fragment == null)return;SupportFragmentManager.BeginTransaction().Replace(Resource.Id.content_frame, fragment).AddToBackStack(null) //支持回退.Commit();}catch(Exception ex){Toast.MakeText(this, "发生异常!异常信息如下:LoadFragment" + ex.Message, ToastLength.Long).Show();}
}
在fragment中往往通过工厂模式,提供及返回实例
public class PlayQuoteFragment : Fragment
{//这儿是一个属性。通过Arguments获取数据public int PlayId => Arguments.GetInt("current_play_id", 0);//这儿是通过工厂模式,提供fragment的实例public static PlayQuoteFragment NewInstance(int playId){//Bundle其实放在这儿,或者放到activity的LoadFragment方法中都是可以的//但放在这儿会更好。若放在activity中,则需要命名不同的Bundle//放在这儿,可以实现对外,只是一个工厂方法和参数即可。外界不需要知道内部的具体事务var bundle = new Bundle();bundle.PutInt("current_play_id", playId);return new PlayQuoteFragment {Arguments = bundle};}public override View OnCreateView(LayoutInflater inflater, ViewGroup container, Bundle savedInstanceState){if (container == null){return null;}var textView = new TextView(Activity);var padding = Convert.ToInt32(TypedValue.ApplyDimension(ComplexUnitType.Dip, 4, Activity.Resources.DisplayMetrics));textView.SetPadding(padding, padding, padding, padding);textView.TextSize = 24;textView.Text = Shakespeare.Dialogue[PlayId];var scroller = new ScrollView(Activity);scroller.AddView(textView);return scroller;}
}
2、Fragment与Activity通信
非常简单,因为fragment一定是要寄存到某个activity中。因此直接使用如下代码:
var myActivity = (MyActivity) this.Activity;
myActivity.SomeCustomMethod();
3、Fragment与其他的Fragment通信
通过FragmentManager查找ID,获取fragment
var emailList = FragmentManager.FindFragmentById<EmailListFragment>(Resource.Id.email_list_fragment);
emailList.SomeCustomMethod(parameter1, parameter2);
相关文章:

Xamarin.Android中的Fragment
目录 1、Activity中使用Fragment2、Fragment与Activity通信3、Fragment与其他的Fragment通信 1、Activity中使用Fragment 一般而言,会在activity中添加一个加载fragment的方法。通过点击菜单的按钮,加载不同的fragment。其样子一般是这样的:…...
portainer初体验
官方文档 安装 docker 这里采用的的是国内汉化的一个镜像,版本号2.16.2。 地址 docker run -d --restartalways --name"portainer" -p 9000:9000 -v /var/run/docker.sock:/var/run/docker.sock 6053537/portainer-ce体验 访问9000端口。 尝试&#x…...
)
4G数传方案(合宙cat1模块)
一. 合宙Cat1简介 合宙 Air724 模组推出的低功耗,超小体积,高性能嵌入式 4G Cat1 核心版,标准的 2.54 排针、最小成本的进项 2G、4G Cat4 切换;主要功能如下: 实际测试工作环境为-35℃-75℃; 支持 5-12V 供电或者 3.7…...

ElasticSearch - 海量数据索引拆分的一些思考
文章目录 困难解决方案初始方案及存在的问题segment merge引入预排序 拆分方案设计考量点如何去除冗余数据按什么维度拆分,拆多少个最终的索引拆分模型演进历程整体迁移流程全量迁移流程流量回放比对验证异步转同步多索引联查优化效果 总结与思考参考 困难 索引数据…...

【SA8295P 源码分析】83 - SA8295P HQNX + Android 完整源代码下载方法介绍
【SA8295P 源码分析】83 - SA8295P HQNX + Android 完整源代码下载方法介绍 一、高通官网 Chipcode 下载步骤介绍1.1 高通Chipcode 下载步骤1.2 高通 ReleaseNote 下载方法二、高通 HQX 代码介绍2.1 完整的 HQX 代码结构:sa8295p-hqx-4-2-4-0_hlos_dev_qnx.tar.gz2.2 sa8295p-…...

【设计模式--原型模式(Prototype Pattern)
一、什么是原型模式 原型模式(Prototype Pattern)是一种创建型设计模式,它的主要目的是通过复制现有对象来创建新的对象,而无需显式地使用构造函数或工厂方法。这种模式允许我们创建一个可定制的原型对象,然后通过复制…...
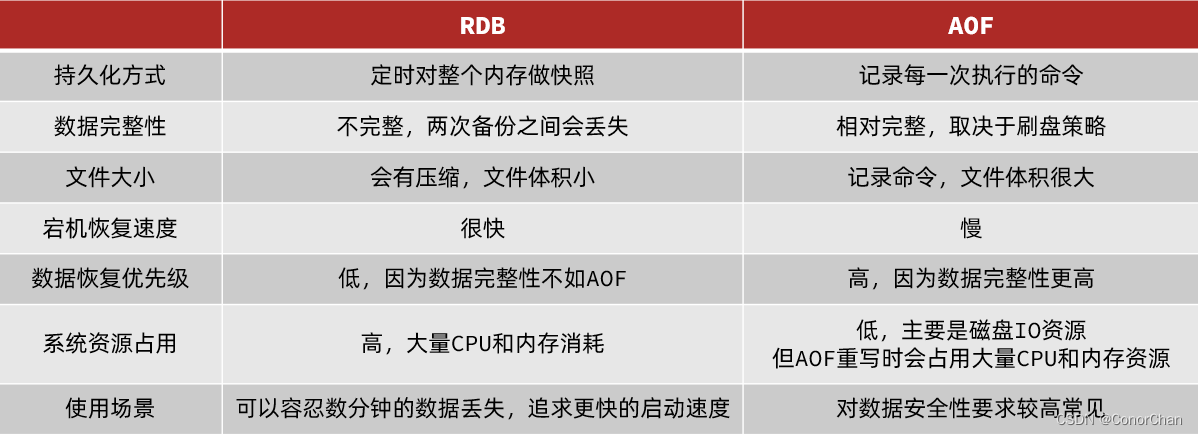
初识 Redis
初识 Redis 1 认识NoSQL1.1 结构化与非结构化1.2 关联和非关联1.3 查询方式1.4. 事务1.5 总结 2 Redis 概述2.1 应用场景2.2 特性 3 Resis 全局命令4 Redis 基本数据类型4.1 String4.1.1 常用命令4.1.2 命令的时间复杂度4.1.3 使用场景 4.2 Hash4.2.1 常用命令4.2.2 命令的时间…...

php灵异事件,啥都没干数据变了?
这篇文章也可以在我的博客查看 搞WordPress,难免跟php打交道 然而这弱类型语言实在坑有点多 这不今儿又踩了个大坑直接时间-1😅 问题 话不多说直接上代码 <?php $items [1,2];foreach ($items as &$item) {/*empty loop*/} print_r($items)…...
)
【ffmpeg】基于需要使用videocapture的opencv编译配置(C++)
目录 配置简介ffmpeg源码编译方法记录gstreamer命令行安装方法opencv的编译项记录 配置简介 opencv使用videocapture读取视频流时,需要借助底层的ffmpeg库。如果不能正确编译,会报错,现记录正确编译配置方法。 ffmpeg源码编译方法记录 ope…...
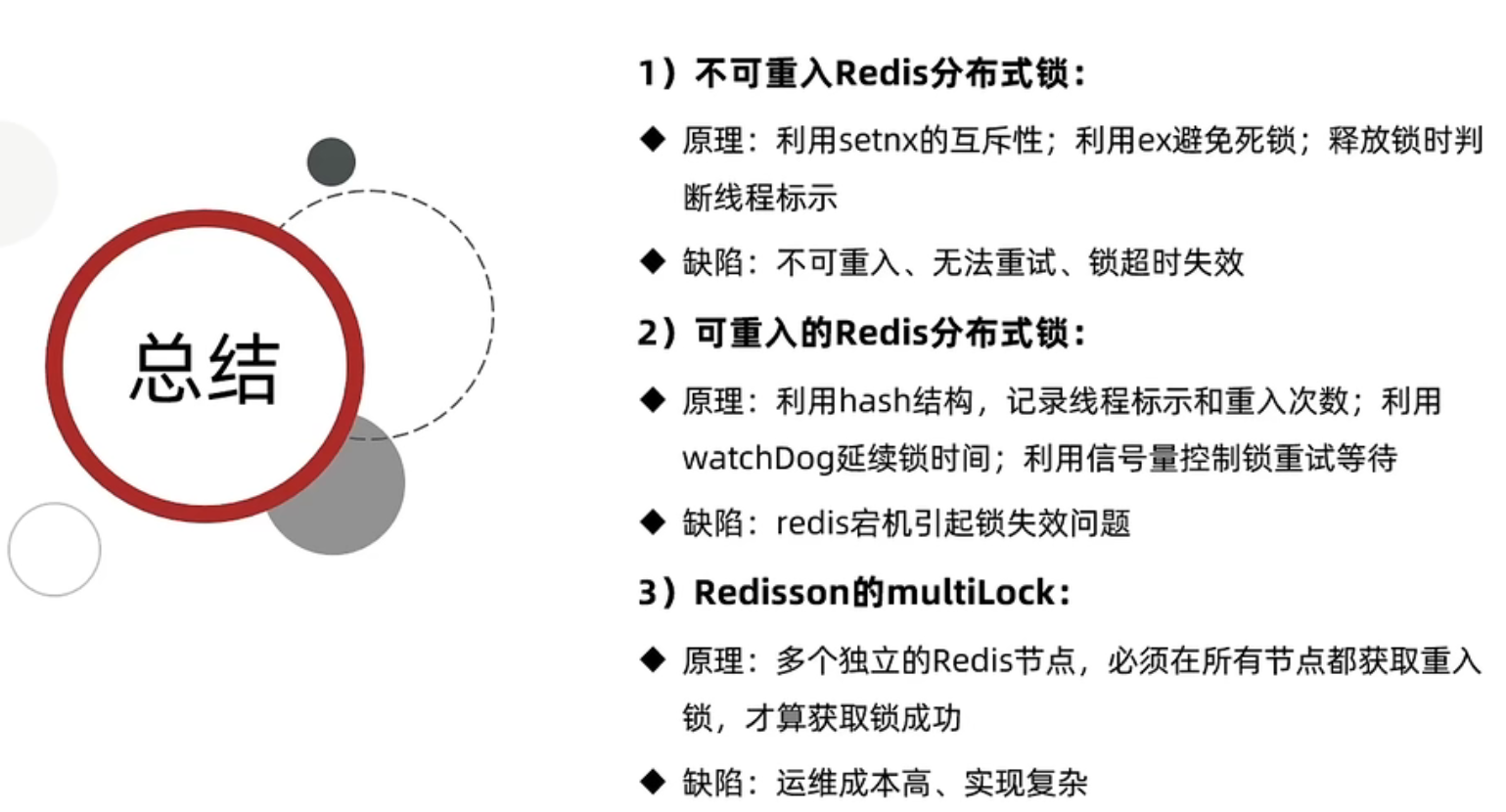
Redisson分布式锁 原理源码 分析
# 基于setnx实现的分布式锁存在的问题: # 为了解决上面的问题,可以用Redisson # Redisson入门 # Redisson可重入锁原理 获取锁的Lua脚本: 释放锁的Lua脚本: # 锁重试原理分析 tryLock()底层代码分析 tim…...

Cocos独立游戏开发框架中的事件管理器
引言 本系列是《8年主程手把手打造Cocos独立游戏开发框架》,欢迎大家关注分享收藏订阅。在独立游戏开发中,事件管理器是一个不可或缺的组件。它为开发者提供了一种灵活的方式来处理游戏内部各种状态变化和用户交互,实现模块之间的解耦和通信…...

keepalived+haproxy 搭建高可用高负载高性能rabbitmq集群
一、环境准备 1. 我这里准备了三台centos7 虚拟机 主机名主机地址软件node-01192.168.157.133rabbitmq、erlang、haproxy、keepalivednode-02192.168.157.134rabbitmq、erlang、haproxy、keepalivednode-03192.168.157.135rabbitmq、erlang 2. 关闭三台机器的防火墙 # 关闭…...

网络安全(黑客)零基础自学
网络安全是什么? 网络安全,顾名思义,网络上的信息安全。 随着信息技术的飞速发展和网络边界的逐渐模糊,关键信息基础设施、重要数据和个人隐私都面临新的威胁和风险。 网络安全工程师要做的,就是保护网络上的信息安…...

如何把本地项目上传github
一、在gitHub上创建新项目 【1】点击添加()-->New repository 【2】填写新项目的配置项 Repository name:项目名称 Description :项目的描述 Choose a license:license 【3】点击确定,项目已在githu…...

跳跃游戏【贪心算法】
跳跃游戏 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。在这里插入图片…...

vue2+element-ui 实现下拉框滚动加载
一、自定义滚动指令。 VUE.directive( el-select-loadmore: { bind(el, binding) { const SELECTWRAP_DOM el.querySelector(.el-select-dropdown .el-select-dropdown__wrap) SELECTWRAP_DOM.addEventListener(scroll, function () { /*…...

探索AIGC人工智能(Midjourney篇)(二)
文章目录 利用Midjourney进行LOGO设计 用ChatGPT和Midjourney的AI绘画,制作儿童绘本故事 探索Midjourney换脸艺术 添加InsightFaceSwap机器人 Midjourney打造专属动漫头像 ChatGPT Midjourney画一幅水墨画 Midjourney包装设计之美 Midjourney24节气海报插画…...
01-Flask-简介及环境准备
Flask-简介及环境准备 前言简介特点Flask 与 Django 的比较环境准备 前言 本篇来介绍下Python的web框架–Flask。 简介 Flask 是一个轻量级的 Web 框架,使用 Python 语言编写,较其他同类型框架更为灵活、轻便且容易上手,小型团队在短时间内…...
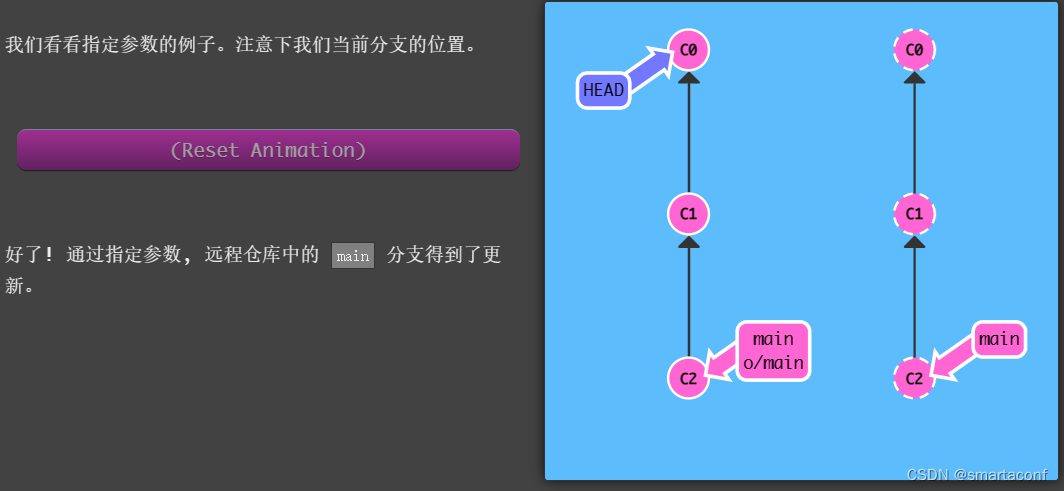
【Git游戏】远程分支
origin/<branch> 远程分支在本地以 origin/<branch>格式存在,他指向上次和远程分支通过时的记录 git checkout origin/<branch> 会出现HEAD分离的情况 与远程通讯 git fetch —— 从远端获取数据(实际上将本地仓库中的远程分支更新…...

Day07-ElementUI
Day02-ElementUI 一 菜单设计 1 静态菜单 a 在components文件夹中新建一个组件Menu.vue <template><div class="menu-wrap"><el-menuclass="el-menu-vertical-demo"background-color="#031627"text-color="#fff"ac…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...
