自然语言处理(一):词嵌入
词嵌入
词嵌入(Word Embedding)是自然语言处理(NLP)中的一种技术,用于将文本中的单词映射到一个低维向量空间中。它是将文本中的单词表示为实数值向量的一种方式。
在传统的文本处理中,通常使用独热编码(One-Hot Encoding)来表示单词,即将每个单词表示为一个稀疏的高维向量,向量中只有一个位置为1,其余位置为0。这种表示方式无法捕捉到单词之间的语义关系和相似性。
而词嵌入通过将单词映射到一个连续的向量空间中,使得具有相似语义的单词在向量空间中的距离更近。这样的表示方式可以更好地表达单词之间的语义关系,并且可以用于计算单词的相似度、聚类、分类等任务。
词嵌入模型通常是通过无监督学习的方式从大规模的文本语料库中学习得到的。一种常用的词嵌入模型是Word2Vec,它使用了神经网络模型来训练词嵌入向量。其他常见的词嵌入模型还包括GloVe、FastText等。
使用预训练的词嵌入模型,可以将文本中的单词转换为对应的词嵌入向量,从而为文本数据提供更丰富的表示。这对于各种NLP任务,如文本分类、命名实体识别、情感分析等,都具有重要的作用,并且可以提升模型的性能和效果。
文章内容来自李沐大神的《动手学深度学习》并加以我的理解,感兴趣可以去https://zh-v2.d2l.ai/查看完整书籍
文章目录
- 词嵌入
- 为什么独热向量是一个糟糕的选择
- 自监督的word2vec
- 跳元模型(Skip-Gram)
- 定义
- 训练
- 连续词袋(CBOW)模型
- 定义
- 训练
为什么独热向量是一个糟糕的选择
-
维度灾难
独热向量需要为每个可能的取值创建一个维度,这样会导致数据集在高维空间中变得非常稀疏。对于具有大量类别或取值的特征,独热编码会导致高维度的输入空间,这会增加模型的复杂性和计算开销。 -
信息损失
独热向量将每个取值都视为独立的特征,忽略了它们之间的相关性。这可能会导致丢失一些重要的信息。
我们一般使用余弦相似度来描述两个向量之间的相关性:
x T y ∣ ∣ x ∣ ∣ ∣ ∣ y ∣ ∣ ∈ [ − 1 , 1 ] \frac{x^Ty}{||x||||y||}\in [-1,1] ∣∣x∣∣∣∣y∣∣xTy∈[−1,1]
若我们使用独热编码,任意两个向量之间的余弦相似度为0. -
统计效率低:独热向量会引入大量的零值,这对于统计建模来说可能是低效的。在数据集中存在大量零值的情况下,计算和存储这些稀疏向量的开销将会增加。
-
增加模型复杂性:独热向量会引入大量的特征维度,这可能导致模型的复杂性增加。对于某些机器学习算法,如决策树和神经网络,高维度的输入空间可能会导致模型过拟合的问题。
自监督的word2vec
为了解决独热编码的问题,我们引入word2vec方法。
Word2Vec 是一种用于将词汇映射到连续向量空间的技术,它是由 Google 在 2013 年开发的一种词嵌入(Word Embedding)方法。Word2Vec 通过学习大规模文本语料库中的上下文信息,将每个单词表示为一个稠密的向量,以便在计算机中更好地处理和理解自然语言。
Word2Vec 有两种主要的模型架构:连续词袋模型(Continuous Bag of Words, CBOW)和跳字模型(Skip-gram)。这两种模型都基于相同的原理:根据上下文单词的共现关系来学习词向量。
-
连续词袋模型(CBOW):CBOW 模型的目标是根据上下文单词来预测目标单词。它将上下文中的单词作为输入,通过一个浅层神经网络模型来学习目标单词的向量表示。
-
跳字模型(Skip-gram):Skip-gram 模型与 CBOW 模型相反,它的目标是根据目标单词来预测上下文单词。它通过训练来学习目标单词和上下文单词之间的关系,以得到每个单词的向量表示。
Word2Vec 使用的核心思想是“共现性”,即假设在语料库中,经常在相似的上下文中出现的单词也具有相似的语义含义。通过学习这种共现关系,Word2Vec 可以生成具有语义信息的词向量。这些词向量可以用于各种自然语言处理任务,如文本分类、命名实体识别、机器翻译等。
Word2Vec 的优点包括:
- 将离散的词汇表示为连续向量,使得单词更容易用数学方式进行处理和计算。
- 通过捕捉上下文关系,生成的词向量可以表达单词的语义和语法信息。
- 可以从大规模的未标记文本数据中自动学习词向量,无需人工标注数据。
- 生成的词向量可以在各种自然语言处理任务中作为特征输入,提高模型的性能。
需要注意的是,Word2Vec 也有一些限制和注意事项,例如对于罕见的单词可能无法得到很好的向量表示,以及在处理多义词时可能存在一定的歧义。此外,对于特定任务,可能需要对生成的词向量进行进一步微调或调整。
总体而言,Word2Vec 是一种非常有用且广泛应用的词嵌入技术,对于许多自然语言处理应用具有重要作用。
跳元模型(Skip-Gram)
定义
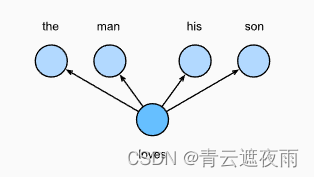
简单来说,跳元模型就是通过假设一个词可以用来在文本序列中生成其周围的单词。以文本序列“the”“man”“loves”“his”“son”为例。假设中心词选择“loves”,并将上下文窗口设置为2,如图所示,给定中心词“loves”,跳元模型考虑生成上下文词“the”“man”“him”“son”的条件概率:
P ( " t h e " , " m a n " , " h i s " , " s o n " ∣ " l o v e " ) P("the","man","his","son"|"love") P("the","man","his","son"∣"love")
若假设上下文词是在给定中心词的情况下独立生成的(即条件独立性)。在这种情况下,上述条件概率可以重写为:
P ( " t h e " ∣ " l o v e " ) ⋅ P ( " m a n " ∣ " l o v e " ) ⋅ P ( " h i s " ∣ " l o v e " ) ⋅ P ( " s o n " ∣ " l o v e " ) P("the"|"love")\cdot P("man"|"love")\cdot P("his"|"love")\cdot P("son"|"love") P("the"∣"love")⋅P("man"∣"love")⋅P("his"∣"love")⋅P("son"∣"love")
在跳元模型中,每个词都有两个 d d d维向量表示,用于计算条件概率。更具体地说,对于词典中索引为 i i i的任何词,分别用 v i ∈ R d v_i\in R^d vi∈Rd和 u i ∈ R d u_i\in R^d ui∈Rd表示其用作中心词和上下文词时的两个向量。给定中心词 w c w_c wc(词典中的索引 c c c),生成任何上下文词 w o w_o wo(词典中的索引 o o o)的条件概率可以通过对向量点积的softmax操作来建模:
P ( w o ∣ w c ) = e x p ( u o T v c ) ∑ i ∈ V e x p ( u i T v c ) P(w_o|w_c)=\frac{exp(u_o^Tv_c)}{\sum_{i\in V}exp(u_i^Tv_c)} P(wo∣wc)=∑i∈Vexp(uiTvc)exp(uoTvc)
其中词表索引集 V = 0 , 1 , . . . , ∣ V ∣ − 1 V={0,1,...,|V|-1} V=0,1,...,∣V∣−1,给定长度为 T T T的文本序列,其中时间步 t t t处的词表示为 w t w^{t} wt。假设上下文词是在给定任何中心词的情况下独立生成的。对于上下文窗口 m m m,跳元模型的似然函数是在给定任何中心词的情况下生成所有上下文词的概率:
∏ t = 1 T ∏ − m ≤ j ≤ m , j ≠ 0 P ( w t + j ∣ w t ) \prod_{t=1}^{T} \prod_{-m\leq j \leq m,j\neq0}P(w^{t+j}|w^{t}) t=1∏T−m≤j≤m,j=0∏P(wt+j∣wt)
其中可以省略小于 1 1 1或大于 t t t的任何时间步。
训练
跳元模型参数是词表中每个词的中心词向量和上下文词向量。在训练中,我们通过最大化似然函数(即极大似然估计)来学习模型参数。这相当于最小化以下损失函数:
− ∑ t = 1 T ∑ − m ≤ j ≤ m , j ≠ 0 l o g P ( w ( t + j ) ∣ w ( t ) ) -\sum_{t=1}^{T}\sum_{-m\leq j \leq m,j\neq0}logP(w^{(t+j)}|w^{(t)}) −t=1∑T−m≤j≤m,j=0∑logP(w(t+j)∣w(t))
当使用随机梯度下降来最小化损失时,在每次迭代中可以随机抽样一个较短的子序列来计算该子序列的(随机)梯度,以更新模型参数。为了计算该(随机)梯度,我们需要获得对数条件概率关于中心词向量和上下文词向量的梯度。通常,涉及中心词 w c w_c wc和上下文词 w o w_o wo的对数条件概率为:
l o g P ( w o ∣ w c ) = u o T v c − l o g ( ∑ i ∈ V e x p ( u i T v c ) ) logP(w_o|w_c)=u_o^Tv_c-log(\sum_{i\in V}exp(u_i^Tv_c)) logP(wo∣wc)=uoTvc−log(i∈V∑exp(uiTvc))
通过微分,我们可以获得其相对于中心词向量 v c v_c vc的梯度为
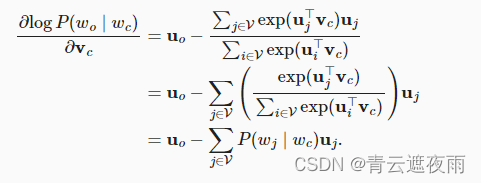
注意, 上式中的计算需要词典中以 w c w_c wc为中心词的所有词的条件概率。其他词向量的梯度可以以相同的方式获得。
对词典中索引为 i i i的词进行训练后,得到 v i v_i vi(作为中心词)和 u i u_i ui(作为上下文词)两个词向量。在自然语言处理应用中,跳元模型的中心词向量通常用作词表示。
对于如何具体使用和训练跳元模型,我将在后面的博客中给出
连续词袋(CBOW)模型
定义
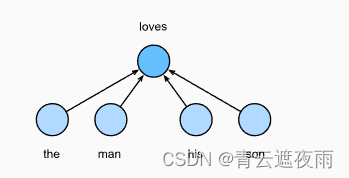
连续词袋(CBOW)模型类似于跳元模型。与跳元模型的主要区别在于,连续词袋模型假设中心词是基于其在文本序列中的周围上下文词生成的。例如,在文本序列“the”“man”“loves”“his”“son”中,在“loves”为中心词且上下文窗口为2的情况下,连续词袋模型考虑基于上下文词“the”“man”“him”“son”(如下图所示)生成中心词“loves”的条件概率,即:
P ( " l o v e " ∣ " t h e " , " m a n " , " h i s " , " s o n " ) P("love"|"the","man","his","son") P("love"∣"the","man","his","son")
由于连续词袋模型中存在多个上下文词,因此在计算条件概率时对这些上下文词向量进行平均。具体地说,对于字典中索引 i i i的任意词,分别用 v i ∈ R d v_i\in R^d vi∈Rd和 u i ∈ R d u_i\in R^d ui∈Rd表示用作上下文词和中心词的两个向量(符号与跳元模型中相反)。给定上下文词 w o 1 , . . . , w o 2 m w_{o1},...,w_{o2m} wo1,...,wo2m(在词表中索引是 o 1 , . . . , o 2 m o1,...,o2m o1,...,o2m)生成任意中心词 w c w_c wc(在词表中索引是 c c c)的条件概率可以由以下公式建模:
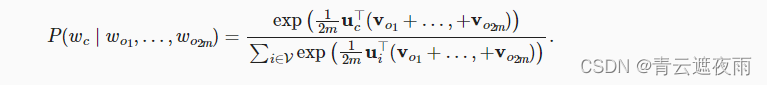
为了简洁起见,我们设为 W o = o 1 , . . , o 2 m W_o={o1,..,o2m} Wo=o1,..,o2m和 v ˉ = ( v o 1 + v o 2 + . . . + v o 2 m ) / ( 2 m ) \bar{v}=(v_o1+v_o2+...+v_{o2m})/(2m) vˉ=(vo1+vo2+...+vo2m)/(2m),那么上述式子可以化简为:
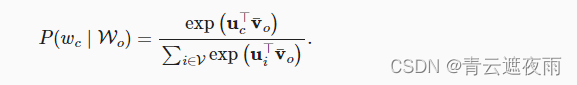
给定长度为 T T T的文本序列,其中时间步 t t t处的词表示为 w t w^{t} wt。对于上下文窗口 m m m,连续词袋模型的似然函数是在给定其上下文词的情况下生成所有中心词的概率:
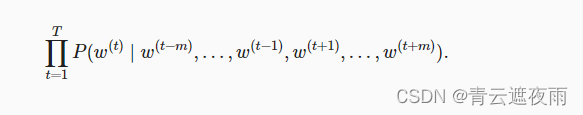
训练
训练连续词袋模型与训练跳元模型几乎是一样的。连续词袋模型的最大似然估计等价于最小化以下损失函数:
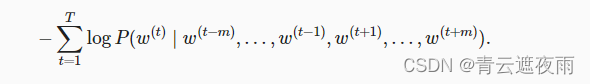
请注意,
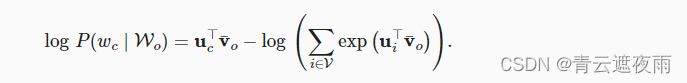
通过微分,我们可以获得其关于任意上下文词向量 v o i v_{oi} voi( i = 1 , 2 , . . . , 2 m i=1,2,...,2m i=1,2,...,2m)的梯度,如下:
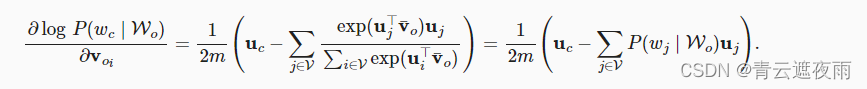
其他词向量的梯度可以以相同的方式获得。与跳元模型不同,连续词袋模型通常使用上下文词向量作为词表示。
相关文章:
自然语言处理(一):词嵌入
词嵌入 词嵌入(Word Embedding)是自然语言处理(NLP)中的一种技术,用于将文本中的单词映射到一个低维向量空间中。它是将文本中的单词表示为实数值向量的一种方式。 在传统的文本处理中,通常使用独热编码&…...
【HSPCIE仿真】HSPICE仿真基础
HSPICE概述 1. HSPICE简介3. 标准输入文件4. 标准输出文件3. HSPCIE仿真过程 1. HSPICE简介 SPICE (Simulation Program with IC Emphasis)是1972 年美国加利福尼亚大学柏克莱分校电机工程和计算机科学系开发 的用于集成电路性能分析的电路模拟程序。 …...
二、前端监控之方案调研
前端监控体系 一个完整的前端监控体系包括了日志采集、日志上报、日志存储、日志切分&计算、数据分析、告警等流程。 对于一名前端开发工程师来说,也就意味着工作不再局限于前端业务的开发工作,需要有Nginx服务运维能力、实时/离线分析能力、Node应…...

npm 创建 node.js 项目
package.json重要说明 package.json是创建任何node.js项目必须要有的一个文件。 因为在package.json文件中,有详细的项目描述, 包括: (1)项目名称:name (2)版本:version (3)依赖文件:dependencies 等…...

JMeter性能测试(上)
一、基础简介 界面 打开方式 双击 jmeter.bat双击 ApacheJMeter.jsr命令行输入 java -jar ApacheJMeter.jar 目录 BIN 目录:存放可执行文件和配置文件 docs目录:api文档,用于开发扩展组件 printable-docs目录:用户帮助手册 li…...

自定义date工具类 DateUtils.java
自定义date工具类 DateUtils.java 简介 Date日期类型的工具类。 api 日期格式化 format(Date date);日期格式化 format(Date date, String pattern);计算距离现在多久,非精确 getTimeBefore(Date date);计算距离现在多久,精确…...
Linux(Ubuntu)安装docker
2017年的3月1号之后,Docker 的版本命名开始发生变化,同时将 CE 版本和 EE 版本进行分开。 Docker社区版(CE):为了开发人员或小团队创建基于容器的应用,与团队成员分享和自动化的开发管道。docker-ce 提供了简单的安装…...
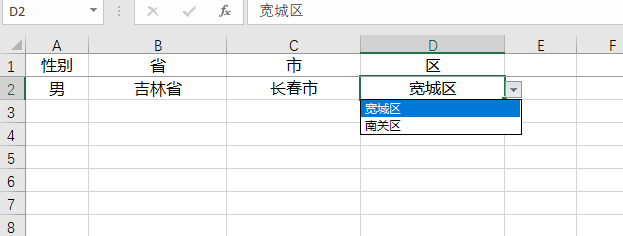
Apache Poi 实现Excel多级联动下拉框
由于最近做的功能,需要将接口返回的数据列表,输出到excel中,以供后续导入,且网上现有的封装,使用起来都较为麻烦,故参考已有做法封装了工具类。 使用apache poi实现excel联动下拉框思路 创建隐藏单元格&a…...

常见的 HTML<meta> 标签的 name 属性及其作用
HTML中的 <meta> 标签可以通过 name 属性提供元数据,这些元数据可以用于指定有关文档的信息,以及控制浏览器和搜索引擎的行为。name 属性通常与其他属性一起使用,如 content、charset、http-equiv 等,以提供更具体的元数据信…...
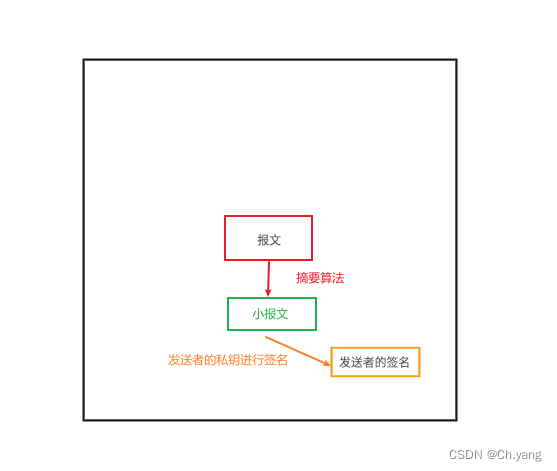
【网络安全】理解报文加密、数字签名能解决的实际问题
文章目录 前言1. 防止报文泄露 —— 加密体系的出现1.1 理解非对称加密体系的实施难点1.2 加密体系的实际应用 2. 防止报文被篡改 —— 数字签名的出现2.1 数字签名的原理2.2 数字签名的实施难点2.2 数字签名的实际应用 —— 引入摘要算法 3. 实体鉴别 —— CA证书 后记 前言 …...

linux中安装nodejs,卸载nodejs,更新nodejs
卸载nodejs 卸载node sudo apt-get remove nodejs清理掉自动安装的并且不需要软件包 sudo apt autoremove查看node相关的文件 sudo whereis node如果有文件需要手动删除文件 删除该文件命令 sudo rm -rf /usr/local/bin/node在此查看node -v 是未找到,说明你已经…...

浅谈Python网络爬虫应对反爬虫的技术对抗
在当今信息时代,数据是非常宝贵的资源。而作为一名专业的 Python 网络爬虫程序猿,在进行网页数据采集时经常会遭遇到各种针对爬虫行为的阻碍和限制,这就需要我们掌握一些应对反爬机制的技术手段。本文将从不同层面介绍如何使用 Python 进行网…...

代理池在过程中一直运行
Hey,爬虫达人们!在爬虫的过程中,要保持代理池的稳定性可不容易。今天就来和大家分享一些实用经验,教你如何让代理池在爬虫过程中一直运行!方法简单易行,让你的爬虫工作更顺畅. 在进行爬虫工作时࿰…...
基于Java+SpringBoot+Vue前后端分离党员教育和管理系统设计和实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...

【flutter直接上传图片到阿里云OSS】
flutter直接上传文件到阿里云需要获取凭证,通过调用阿里云获取凭证的接口能拿到下面这些参数 {"StatusCode": 200,"AccessKeyId": "STS.NSsrKZes4cqm.....","AccessKeySecret": "7eGnLZaEFsRCGYJAnrtdE9n....."…...
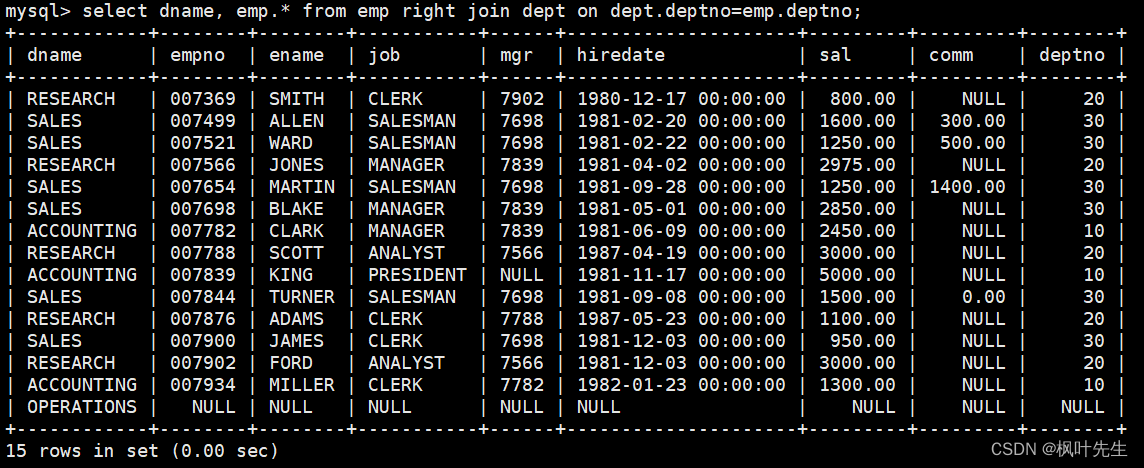
【MySQL系列】表的内连接和外连接学习
「前言」文章内容大致是对MySQL表的内连接和外连接。 「归属专栏」MySQL 「主页链接」个人主页 「笔者」枫叶先生(fy) 目录 一、内连接二、外连接2.1 左外连接2.2 右外连接 一、内连接 内连接实际上就是利用where子句对两种表形成的笛卡儿积进行筛选,前面篇章学习的…...

C语言日常刷题 3
文章目录 题目答案与解析1234、5、6、 题目 1.已知函数的原型是: int fun(char b[10], int *a); ,设定义: char c[10];int d; ,正确的调用语句是( ) A: fun(c,&d); B: fun(c,d); C: fun(&c,&d…...

.net6中, 用数据属性事件触发 用httpclient向服务器提交Mes工单
MES开发中, 客户往往会要求 工单开始时记录工艺数据, 工单结束时将这些工艺数据回传到更上一级的WES系统中. 因为MES系统和PLC 是多线程读取, 所以加锁, 事件触发是常用手段. using MyWebApiTest.PLC; using MyWebApiTest.Service; using MyWebApiTest.Service.Entry; using M…...
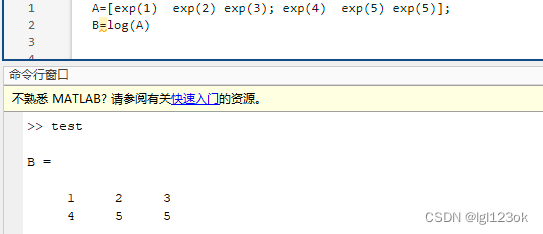
sin(A)的意义
若存在矩阵A,则sin(A)表示对于矩阵A的每一个元素,进行对应的函数运算。 如:...
ctfshow-web14
0x00 前言 CTF 加解密合集CTF Web合集 0x01 题目 0x02 Write Up 首先看到这个,swith,那么直接输入4,则会打印$url的值 然后访问一下 查看一下,发现完整的请求是http://c7ff9ed6-dccd-4d01-907a-f1c61c016c15.challenge.ctf.sho…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
