【算法系列总结之分组循环篇】
【算法系列总结之分组循环篇】
- 分组循环
- 1446.连续字符
- 1869.哪种连续子字符串更长
- 1957.删除字符使字符串变好
- 2038.如果相邻两个颜色均相同则删除当前颜色
- 1759.统计同质子字符串的数目
- 2110.股票平滑下跌阶段的数目
- 1578.使绳子变成彩色的最短时间
- 1839.所有元音按顺序排布的最长子字符串
- 2760.最长奇偶子数组
- 2765.最长交替子序列
- 228.汇总区间
分组循环
分组循环指的是将整个数组或者字符串分为很多片段,这些片段的判断处理逻辑是一样的。分组循环需要使用同向双指针,但是与滑动窗口不同的是,滑动窗口是收集左右区间内连续数组或者字符串,当不满足收集要求时移动右指针,而当满足后移动左指针,此时左指针移动到原来左指针的下一位,而分组循环是左指针移动到右指针下一位。
// 模板 l、r分别表示左右指针int l=0,r=0;while(r<n){// 每一次求新区间则重新赋值ll=r;// r表示最长连续区间最后一个while(r<n-1&&s[r]==s[r+1])r++;// 求完区间后收集结果res=max(r-l+1,res);// 并移动r到下一个r++;}
1446.连续字符
思路:分组循环,相当于把字符串分为多个连续相同字符片段,利用左右端点l、r求解最长连续相同字符片段长度。
class Solution {
public:int maxPower(string s) {int n=s.size();int l=0,r=0;int res=0;while(r<n){// 每一次求新区间则重新赋值ll=r;// r表示最长连续区间最后一个while(r<n-1&&s[r]==s[r+1])r++;// 求完区间后收集结果res=max(r-l+1,res);// 并移动r到下一个r++;}return res;}
};
1869.哪种连续子字符串更长
思路:分组循环,相当于把字符串分为多个连续1或者0字符片段,利用左右端点l、r和元素s[l]求解最长连续1或者0字符片段长度,再根据条件返回对应结果。
class Solution {
public:bool checkZeroOnes(string s) {// 分别记录最长1、最长0长度int num1=0,num0=0;int n=s.size();// 区间左右端点int l=0,r=0;while(r<n){// l表示每轮左区间l=r;// r表示当前符合条件区间右端点while(r<n-1&&s[r]==s[r+1])r++;// 收集0或者1长度if(s[l]=='0')num0=max(num0,r-l+1);elsenum1=max(num1,r-l+1);r++;}return num1>num0;}
};
1957.删除字符使字符串变好
思路:分组循环,相当于把字符串分为多个连续相同片段,利用左右端点l、r求解每一个连续相同片段长度,如果长度小于3则直接将该片段加入结果,反之则只加入两个字符即可。
class Solution {
public:string makeFancyString(string s) {string res;int n=s.size();int l=0,r=0;while(r<n){l=r;while(r<n-1&&s[r]==s[r+1])r++;if(r-l+1<3)res+=s.substr(l,r-l+1);else {// 加入两次res.push_back(s[l]);res.push_back(s[l]);}r++;}return res;}
};
2038.如果相邻两个颜色均相同则删除当前颜色
思路:分组循环,相当于把字符串分为多个连续A或者B字符片段,利用左右端点l、r和元素colors[l]求解最长连续A或者B字符片段可选择的次数,再根据条件返回对应结果。注意,最长连续A或者B字符片段可选择的次数为在保留左右两边字符的情况下中间所有剩余字符,即一旦长度大于等于3则为长度减去2,反之则为0,由于A是先手,故A必须严格大于B。
class Solution {
public:bool winnerOfGame(string colors) {int n=colors.size();// 转换为次数int numA=0,numB=0;int l=0,r=0;while(r<n){l=r;while(r<n-1&&colors[r]==colors[r+1])r++;// 一旦>=3 则可移动的为长度减去左右两边2if(colors[l]=='A')numA+=(r-l+1)>=3?(r-l+1)-2:0;elsenumB+=(r-l+1)>=3?(r-l+1)-2:0;r++;}return numA>numB;}
};
1759.统计同质子字符串的数目
思路:分组循环,相当于把字符串分为多个连续相同片段,利用左右端点l、r求解每一个连续相同片段长度,然后利用1、3、6、10、15…规律根据长度n求出方案数n*(n+1)/2,最后累计方案数即可。
class Solution {
public:const long long NUM=1e9+7;int countHomogenous(string s) {// 1 3 6 10 15 n*(n+1)/2int n=s.size();int l=0,r=0;// long long 避免精度不够long long res=0;while(r<n){l=r;while(r<n-1&&s[r]==s[r+1])r++;int len=r-l+1;// 注意取模res+=(long long)(len+1)*len/2;r++;}// 取模return res%NUM;}
};
2110.股票平滑下跌阶段的数目
思路:分组循环,相当于把数组分为多个连续公差为1的递减片段,利用左右端点l、r求解每一个连续公差为1的递减片段长度,然后利用1、3、6、10、15…规律根据长度n求出方案数n*(n+1)/2,最后累计方案数即可。
class Solution {
public:long long getDescentPeriods(vector<int>& prices) {int n=prices.size();int l=0,r=0;long long res=0;while(r<n){l=r;// 当前日比前一日股价少一while(r<n-1&&prices[r]==prices[r+1]+1)r++;long long len=r-l+1;res+=len*(len+1)/2;r++;}return res;}
};
1578.使绳子变成彩色的最短时间
思路:分组循环,相当于把绳子分为多个连续相同气球片段,利用左右端点l、r求解每一个连续相同气球片段,并对每个大于1的片段求解总时间和最大时间从而得到最小时间,对这些时间累加即可得到结果。
class Solution {
public:int minCost(string colors, vector<int>& neededTime) {int n=colors.size();int l=0,r=0;int res=0;while(r<n){l=r;while(r<n-1&&colors[r]==colors[r+1])r++;if(l!=r){int maxn=0;for(int i=l;i<=r;i++){maxn=max(neededTime[i],maxn);res+=neededTime[i];}res-=maxn;}r++;}return res;}
};
1839.所有元音按顺序排布的最长子字符串
思路:分组循环,相当于把字符串分为多个按照元音字母递增的至少含有所有元音字母各一个的字符串,与前面几题不同的是,该题需要在记录符合区间的同时,也使用uset来记录元音字母个数,从而便于后序收集结果条件各个元音字母至少一个的判断。
class Solution {
public:int longestBeautifulSubstring(string word) {int n=word.size();int l=0,r=0;int res=0;while(r<n){l=r;// 存储次数 保证各个字母至少出现一次unordered_set<int> uset;// 按照 a e i o u顺序while(r<n-1&&word[r+1]>=word[r]){uset.emplace(word[r]);r++;}// 加入最后一个 前几题都是只需r++ 不需额外处理uset.emplace(word[r]);// cout<<uset.size()<<endl;if(uset.size()==5)res=max(res,r-l+1);r++;}return res;}
};
2760.最长奇偶子数组
思路:分组循环,相当于把数组分为多个[l,r]区间,其中求出满足题目要求的长度最长的[l,r]区间。该题与上述题目不同的地方在于,该题中存在l、[l,r-1]、[l,r]三个判断,由于此处的差异就会导致在处理判断边界条件时可能会出现些许差异和错误。此处首先对于l不满足的情况进行特殊处理,由于已经处理过l,那么后续就是在l满足条件的情况下进行,此时将r加一,相当于比较r和r-1,而不是原先的r和r+1,那么相应的此处得到的r就是第一个不满足的,对应的长度变为r-l,同时也不需要继续对r++啦。(注意细节)
class Solution {
public:int longestAlternatingSubarray(vector<int>& nums, int threshold) {int n=nums.size();int l=0,r=0;int res=0;while(r<n){// 左区间都不满足情况直接下一个if(nums[r]%2!=0||nums[r]>threshold){// continue之前记得r++啊否则区间不动r++;continue;}// 此处才更新左区间l=r;// 左区间已经满足 此时r+1r+=1;// r是第一个不满足的 故此时长度为r-l 并且后续不需要r++while(r<n&&nums[r]<=threshold&&(nums[r]%2!=nums[r-1]%2))r++;res=max(res,r-l);}return res;}
};
2765.最长交替子序列
思路:分组循环,相当于把数组分为多个[l,r]区间,其中求出满足题目要求的长度最长的[l,r]区间。该题与2760不同的地方在于,该题所分得的区间可能重叠喔,比如2 3 4 3 4,其中2 3和3 4 3 4其重叠一个,但是其最多也只会重叠一个,故我们找到第一个不满足的r后回退1即可。建议在分组循环类别的题目中,遇到给区间[l,r]设置条件时先对首部条件进行不合法判断处理再继续喔!
class Solution {
public:int alternatingSubarray(vector<int>& nums) {int n=nums.size();int l=0,r=0;int res=-1;// 数组长度至少为2!!!while(r+1<n){// 排除s1!=s0+1的情况if(nums[r+1]-nums[r]!=1){r++;continue;}// 记录左端点l=r;r+=1; // 右端点加一 至少长度为2int m=1;// r是第一个不满足的while(r<n&&nums[r]-nums[r-1]==m){r++;m*=-1;}res=max(res,r-l);// 2 3 4 3 4 // 2 3和3 4 3 4重合一个 为什么能保证最多重复一个r-=1; // 所以r需要回退一个}return res;}
};
总结:灵老师的nums[i]==nums[i0+(i-i0)%2]也很灵性!!!
228.汇总区间
思路:分组循环,相当于把字符串分为多个连续公差为1的递增片段,利用左右端点l、r求解每一个连续公差为1的递增片段两端,并按照要求格式加入结果。
class Solution {
public:vector<string> summaryRanges(vector<int>& nums) {int n=nums.size();int r=0,l;string tmp;vector<string> res;// l 左端點 r右端點 同向雙指針while(r<n){l=r;while(r<n-1&&nums[r]+1==nums[r+1])r++;tmp=to_string(nums[l]);if(l<r)tmp+="->"+to_string(nums[r]);res.push_back(tmp);r++;}return res;}
};
有一说一,虽然现在力扣刷了四百多题,牛客刷了两百多题,包括前端和算法,但还是觉得遇到一些脑筋急转弯的简单或者中等题还是不会,对于一些题型也没有形成自己的解题思路逻辑,遇到困难题也是要看题解才行,除非自己刷过几次,感觉好挫败啊呜呜呜呜呜呜呜呜,要怎么办!!!
相关文章:

【算法系列总结之分组循环篇】
【算法系列总结之分组循环篇】 分组循环1446.连续字符1869.哪种连续子字符串更长1957.删除字符使字符串变好2038.如果相邻两个颜色均相同则删除当前颜色1759.统计同质子字符串的数目2110.股票平滑下跌阶段的数目1578.使绳子变成彩色的最短时间1839.所有元音按顺序排布的最长子字…...
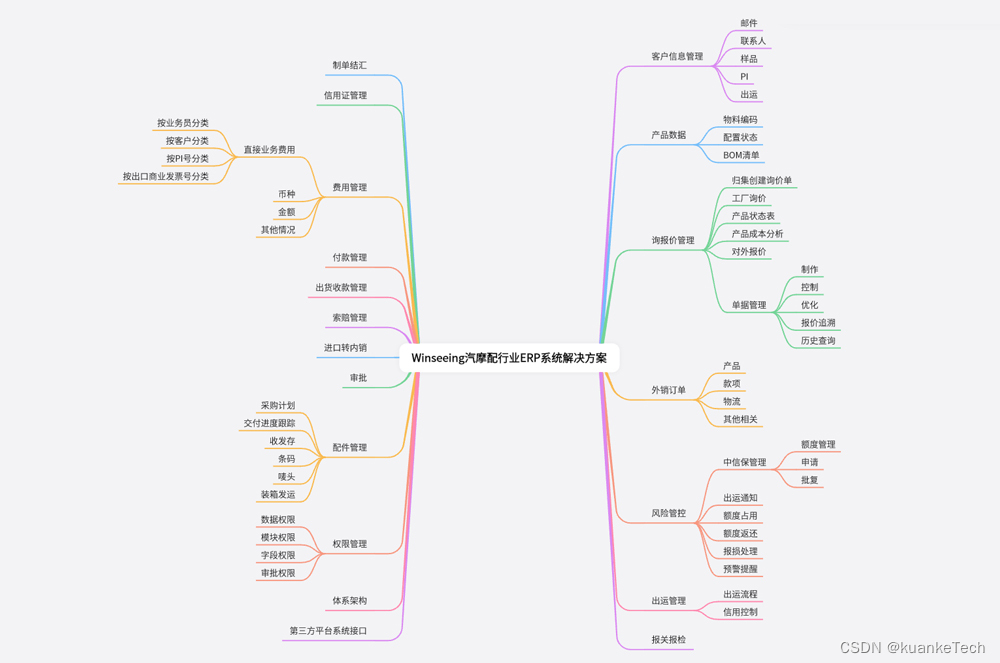
汽车摩托车零部件出口管理ERP解决方案
近年来,随着全球经济的发展,人们对交通工具的需求增加,国内汽车、摩托车市场的不断扩大,以及国内制造技术的不断提高,中国汽车、摩托车零部件出口业务迎来了广阔的发展前景,带动了汽车配件和摩托车配件市场…...

NPM 管理组织包
目录 1、关于组织范围和包 1.1 管理无作用域的包 2、使用组织设置配置npm客户端 2.1 配置您的npm客户端以使用您组织的范围 为所有新包设置组织范围 为单个包设置组织范围 2.2 将默认包可见性更改为public 将单个包的包可见性设置为public 将所有包的包可见性设置为pu…...
)
蓝桥杯上岸每日N题 (修剪灌木)
大家好 我是寸铁 希望这篇题解对你有用,麻烦动动手指点个赞或关注,感谢您的关注 不清楚蓝桥杯考什么的点点下方👇 考点秘籍 想背纯享模版的伙伴们点点下方👇 蓝桥杯省一你一定不能错过的模板大全(第一期) 蓝桥杯省一你一定不…...
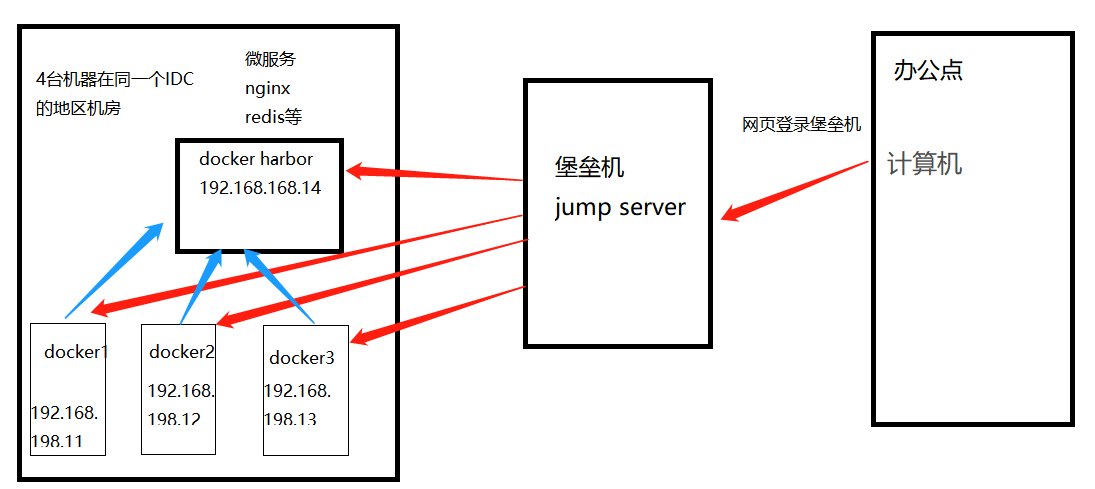
docker harbor私有库
目录 一.Harbor介绍 二.Harbor的特性 三.Harbor的构成 四.Harbor构建Docker私有仓库 4.2在Server主机上部署Harbor服务(192.168.158.25) 4.2.1 这时候这边就可以去查看192.168.158.25网页 4.3此时可真机访问serverIP 4.4通过127.0.0.1来登陆和推送镜…...

strcmp 的使用和模拟
目录 函数介绍: 头文件: 语法: 代码演示: 函数模拟: 函数介绍: strcmp是比较大小的函数。从字符串开始进行比较,如果两个相同位置的字符相同,那么继续往下进行比较,…...

军用加固计算机
军用加固计算机是为满足军事应用需求而设计的一种高性能、高安全性的计算机。与普通计算机相比,它具有以下特点: 加固材料:军用加固计算机通常采用钢板、铝合金等材料进行加固,能够承受较大的冲击和振动,保证在恶劣环境…...

block层:5. 请求分配
请求相关 源码基于5.10 1. 分配请求 static struct request *__blk_mq_alloc_request(struct blk_mq_alloc_data *data) {// 请求队列struct request_queue *q data->q;// 电梯struct elevator_queue *e q->elevator;u64 alloc_time_ns 0;unsigned int tag;// 判断…...
 测试点全过)
L1-038 新世界(Python实现) 测试点全过
题目 这道超级简单的题目没有任何输入。 你只需要在第一行中输出程序员钦定名言“Hello World”,并且在第二行中输出更新版的“Hello New World”就可以了。 输入样例: 无输出样例: Hello World Hello New World题解 """…...
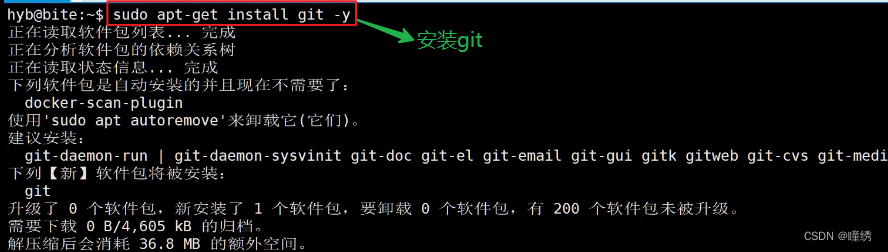
【hello git】初识Git
目录 一、简述Git 二、Linux 下 Git 的安装:CentOS 2.1 基本命令 2.2 示例: 三、Linux 下 Git 的安装:ubuntu 3.1 基本命令 3.2 示例: 一、简述Git Git :版本控制器,记录每次的修改以及版本迭代的一个管…...

Vueelementui动态渲染Radio,Checkbox,笔记
<div id"app"><el-card style"width: 300px"><el-form label-position"top" size"mini"><el-form-item label"标题"><el-input></el-input></el-form-item><el-form-item v-f…...
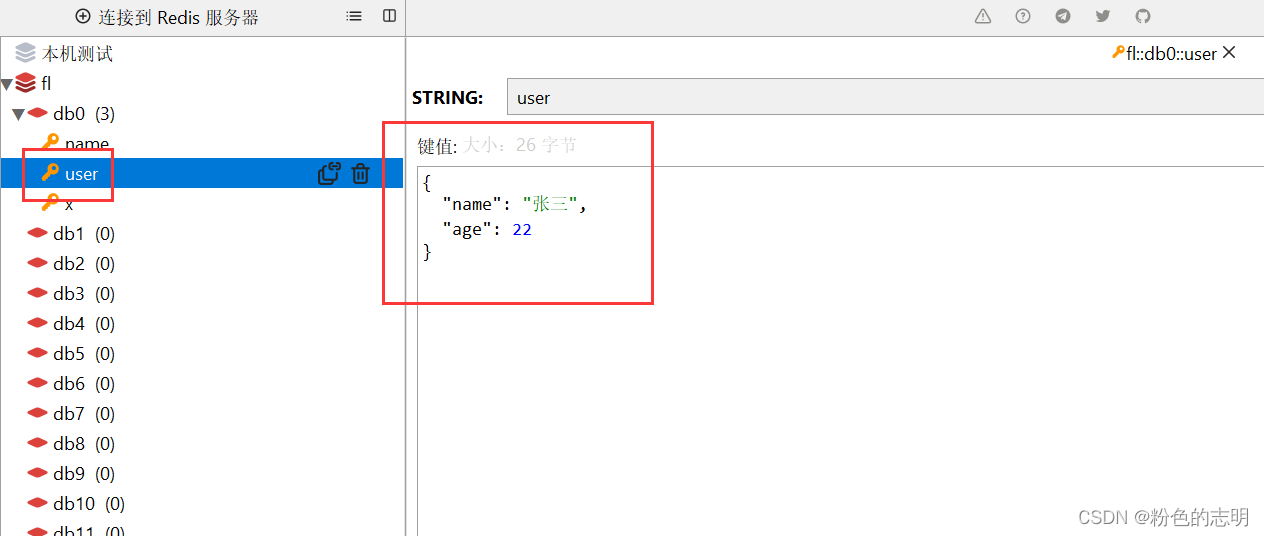
SpringDataRedis 使用
1. SpringDataRedis 特点2. 使用 SpringDataRedis 步骤3. 自定义 RedisTemplate 序列化4. SpringDataRedis 操作对象 1. SpringDataRedis 特点 提供了对不同 Redis 客户端的整合(Lettuce 和 Jedis)提供了 RedisTemplate 统一 API 来操作 Redis支持 Redi…...
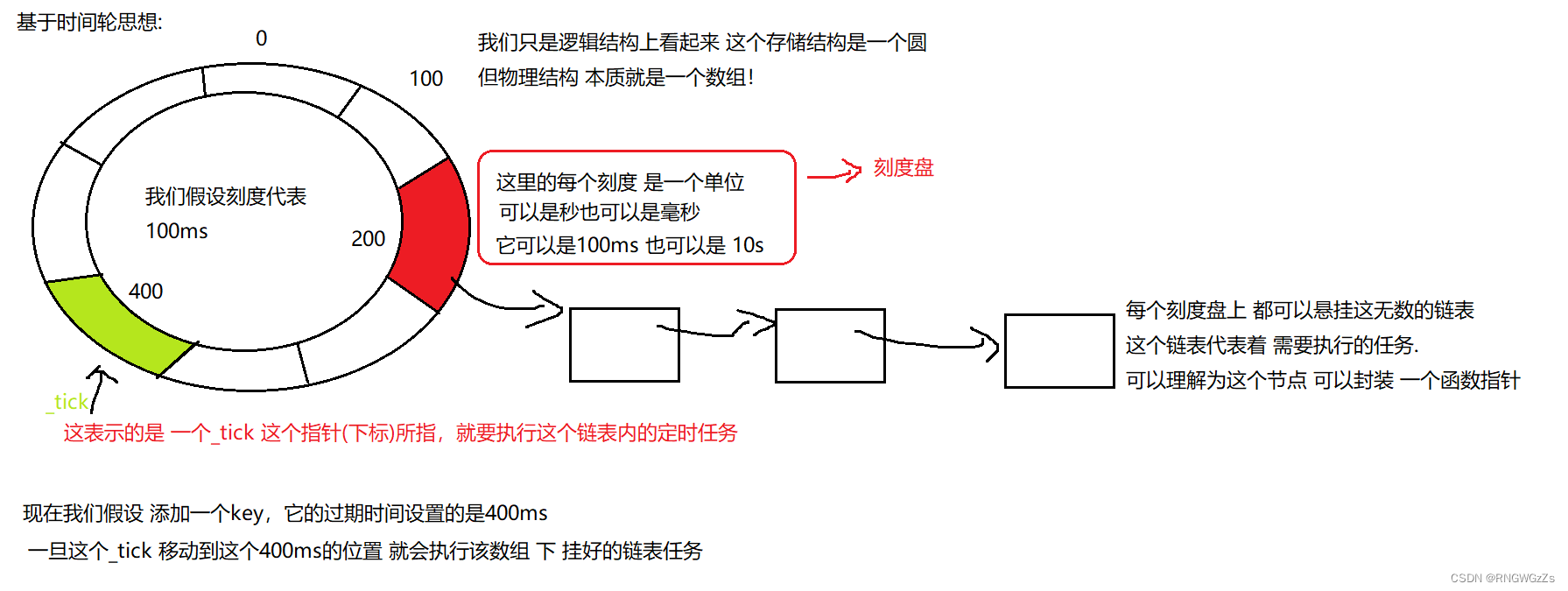
Redis全局命令与数据结构
"那篝火在银河尽头~" Redis-cli命令启动 现如今,我们已经启动了Redis服务,下⾯将介绍如何使⽤redis-cli连接、操作Redis服务。客户端与服务端交互的方式有两种: ● 第⼀种是交互式⽅式: 后续所有的操作都是通过交互式的⽅式实现,…...
LibreOffice新一代的办公软件for Mac/Windows免费版
LibreOffice是一款免费、开源的办公软件套件,可在多个操作系统上运行,包括Windows、Mac和Linux。它提供了一系列功能强大的办公工具,包括文档处理、电子表格、演示文稿、数据库管理等。 LibreOffice的界面简洁直观,与其他流行的办…...
)
Python|OpenCV-读取视频,显示视频并保存视频(3)
前言 本文是该专栏的第3篇,后面将持续分享OpenCV计算机视觉的干货知识,记得关注。 在使用OpenCV处理视频的时候,不论是摄像头画面还是视频文件,通常情况下都要使用VideoCapture类来进行每一帧图像的处理。对于OpenCV而言,只要使用视频文件作为参数,它就可以打开视频文件…...
上传WSL项目到gitlab
上传WSL项目到gitlab 设置ssh将SSH公钥添加到Gitlab 将WSL上的代码上传到gitlab确保在WSL环境中安装了git下面是上传代码到GitLab的具体步骤: 可能遇到的各种错误 设置ssh Gitlab添加SSH KEY 什么是SSH ? SSH 是一种网络协议,具备协议级别的认证及会话…...

从0开始做yolov5模型剪枝
文章目录 从0开始做yolov5模型剪枝 ****1 前言2 GitHub取源码3 原理3.1 原理3.2 network slimming过程 4 具体实施步骤4.1 安装虚拟环境4.2 配置参数4.2.1 数据集参数4.2.2 模型结构参数4.2.3 train.py中的参数 4.3 正常训练4.3.1 准备4.3.2 训练及问题解决 4.4 稀疏化训练4.4.…...
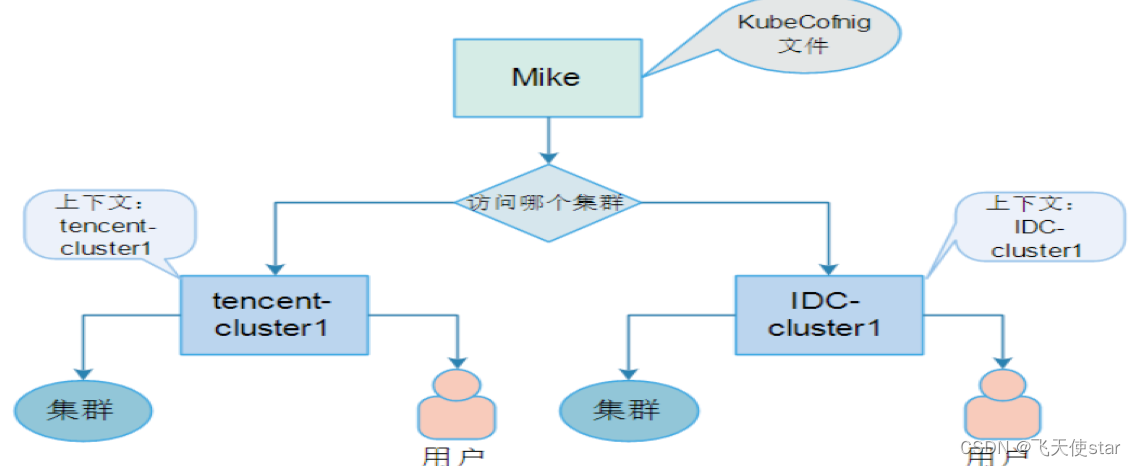
飞天使-k8s基础组件分析-安全
文章目录 名称空间解释访问kubernetes API的控制RBAC的介绍 kubeconfig用户的创建集群默认角色 给组创建授权针对pod配置服务账户参考文档 名称空间解释 名字是啥? 答:集群中每个对象的名称对于该类型的资源都是唯一的。并且每一个对象在整个集群中也有…...
Mysql安装使用
Mysql下载: MySQL :: Download MySQL Community Server Mysql解压: 解压后在根目录新建data文件夹和新建my.ini文件 my.ini文件内容如下: 注意:记得修改目录位置 [mysqld] # 设置3306端口 port3306 # 设置mysql的安装目录 basedirD:\\mysql-5.7.30…...

聚类分析 | MATLAB实现基于LP拉普拉斯映射的聚类可视化
聚类分析 | MATLAB实现基于LP拉普拉斯映射的聚类可视化 目录 聚类分析 | MATLAB实现基于LP拉普拉斯映射的聚类可视化效果一览基本介绍程序设计参考资料 效果一览 基本介绍 聚类分析 | MATLAB实现基于LP拉普拉斯映射的聚类可视化,聚类结果可视化,MATLAB程…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
