⌈算法进阶⌋图论::拓扑排序(Topological Sorting)——快速理解到熟练运用
目录
一、原理
1. 引例:207.课程表
2. 应用场景
3. 代码思路
二、代码模板
三、练习
1、210.课程表Ⅱ🟢
2、2392.给定条件下构造举证🟡
3、310.最小高度树 🟡
一、原理
1. 引例:207.课程表
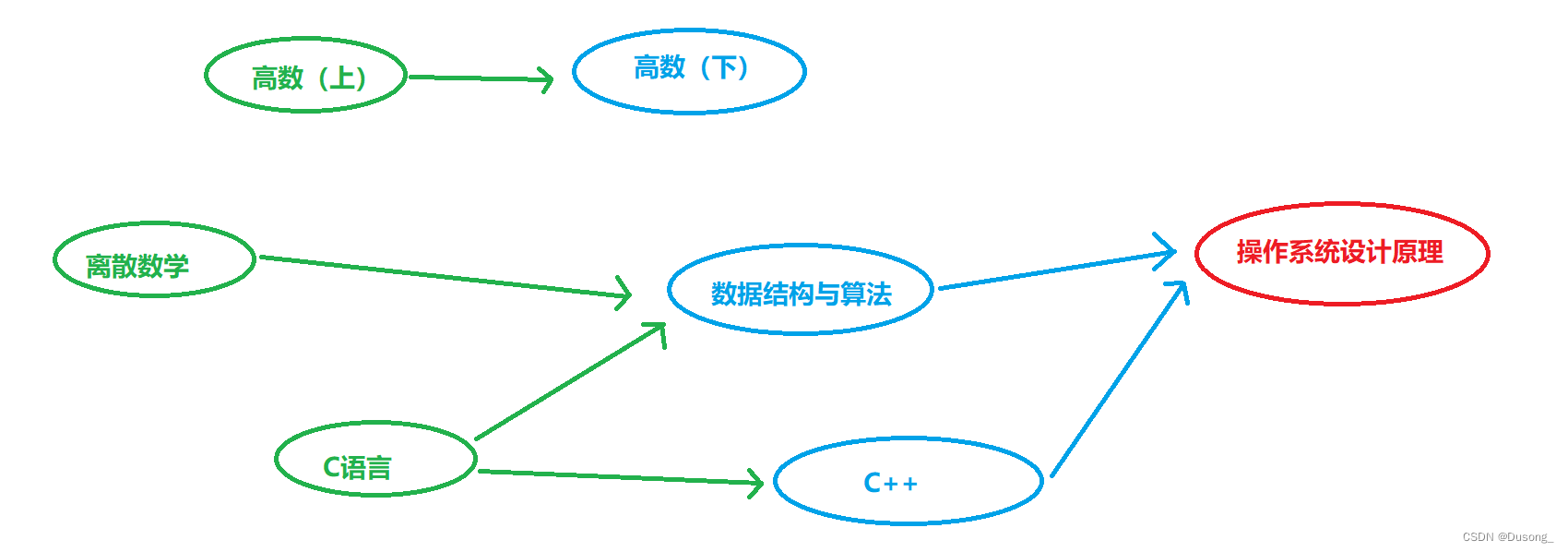
就如大学课程安排一样,如果要学习数据结构与算法、机器学习这类课程,肯定要先学习C语言、Python、离散数学、概率论等等,我们将类似的“推导”关系建如下有向简单图⬇️
2. 应用场景
根据节点的入度大小,拓扑排序主要用于处理先后问题(拓扑序列),以及判断图中是否有环的问题;
3. 代码思路
用大小为节点个数的数组记录每个节点的入度,用队列存放入度为0的节点,遍历这些节点,将这些节点指向的节点的入度-1,最后在记录入度减为0的节点,重复上述步骤;
①拓扑序列:在循环过程中向一数组中push入度为0的节点,排在数组前的节点即为入度先被减为0的节点;
②是否存在环:若拓扑序列数组大小等于节点总个数则说明图中无环;反之,这说明图有环
二、代码模板
/*这里用课程表一题的代码当作模板*/
class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {vector<vector<int>> g(numCourses);int in_degree[numCourses]; //记录节点的入度memset(in_degree, 0, sizeof(in_degree));for (auto& e : prerequisites) {int x = e[0], y = e[1]; //建图g[x].push_back(y);in_degree[y]++; // x -> y ,则y节点入度+1}vector<int> order;queue<int> q;for(int i = 0; i < numCourses; i++) if (in_degree[i] == 0) q.push(i); //将入度为0的节点加入到队列中while (!q.empty()) {int x = q.front();q.pop();order.push_back(x); //push到拓扑序列中for (auto y : g[x]) {in_degree[y]--; //x -> y , 即将y入度-1if (in_degree[y] == 0) q.push(y);}}return order.size() == numCourses; //判断是否有环}
};
三、练习
1、210.课程表Ⅱ🟢
现在你总共有
numCourses门课需要选,记为0到numCourses - 1。给你一个数组prerequisites,其中prerequisites[i] = [ai, bi],表示在选修课程ai前 必须 先选修bi。
- 例如,想要学习课程
0,你需要先完成课程1,我们用一个匹配来表示:[0,1]。返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
示例:
输入:numCourses = 2, prerequisites = [[1,0]] 输出:[0,1] 解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为[0,1] 。
解题思路: 与课程表Ⅰ思路基本一样,依次取出入度为0的节点加入到答案数组中,若数组大小与总结点个数不相同,则说明图中有环,返回空数组。
class Solution {
public:vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {vector<vector<int>> g(numCourses);int in_degree[numCourses];memset(in_degree, 0, sizeof(in_degree));for (auto& e : prerequisites) {int x = e[1], y = e[0];g[x].push_back(y);in_degree[y]++;}vector<int> order;queue<int> q;for(int i = 0; i < numCourses; i++) if (in_degree[i] == 0) q.push(i);while (!q.empty()) {int x = q.front();q.pop();order.push_back(x);for (auto y : g[x]) {in_degree[y]--;if (in_degree[y] == 0) q.push(y);}}return order.size() == numCourses ? order : vector<int>();}
};2、2392.给定条件下构造举证🟡
给你一个 正 整数
k,同时给你:
- 一个大小为
n的二维整数数组rowConditions,其中rowConditions[i] = [abovei, belowi]- 一个大小为
m的二维整数数组colConditions,其中colConditions[i] = [lefti, righti]。两个数组里的整数都是
1到k之间的数字。你需要构造一个
k x k的矩阵,1到k每个数字需要 恰好出现一次 。剩余的数字都是0。矩阵还需要满足以下条件:
- 对于所有
0到n - 1之间的下标i,数字abovei所在的 行 必须在数字belowi所在行的上面。- 对于所有
0到m - 1之间的下标i,数字lefti所在的 列 必须在数字righti所在列的左边。返回满足上述要求的 任意 矩阵。如果不存在答案,返回一个空的矩阵。
示例:
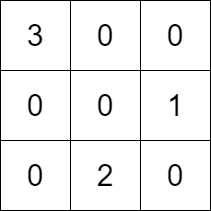
输入:k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]] 输出:[[3,0,0],[0,0,1],[0,2,0]] 解释:上图为一个符合所有条件的矩阵。 行要求如下: - 数字 1 在第 1 行,数字 2 在第 2 行,1 在 2 的上面。 - 数字 3 在第 0 行,数字 2 在第 2 行,3 在 2 的上面。 列要求如下: - 数字 2 在第 1 列,数字 1 在第 2 列,2 在 1 的左边。 - 数字 3 在第 0 列,数字 2 在第 1 列,3 在 2 的左边。 注意,可能有多种正确的答案。
解题思路:该题很明显是处理先后的问题,我们分别处理行与列,分别得到行与列拓扑序列,最后通过一个数组转换,将下标作为节点,对应的值作为该节点位于行/列的位置;
class Solution {
public:vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {vector<int> roworder, colorder;function<bool(vector<vector<int>>&, vector<int>&)> topo_sort = [&](vector<vector<int>>& edge, vector<int>& order) -> bool{vector<vector<int>> g(k);int in_deg[k];memset(left, 0, sizeof(left));for (auto& e : edge) {int x = e[0]-1, y = e[1] - 1;g[x].push_back(y);in_deg[y]++;}queue<int> q;for(int i = 0; i < k; i++) if (in_deg[i] == 0) q.push(i);while (!q.empty()) {int x = q.front();q.pop();order.push_back(x);for (auto y : g[x]) {in_deg[y]--;if (in_deg[y] == 0) q.push(y);}}return order.size() == k;};vector<vector<int>> ans(k, vector<int>(k, 0));if (!topo_sort(rowConditions, roworder) || !topo_sort(colConditions, colorder)) return {};int row[k], col[k];for (int i = 0; i < k; i++) {row[roworder[i]] = i;col[colorder[i]] = i;}for (int i = 0; i < k; i++) {ans[row[i]][col[i]] = i + 1;}return ans;}
};3、310.最小高度树🟡
树是一个无向图,其中任何两个顶点只通过一条路径连接。 换句话说,一个任何没有简单环路的连通图都是一棵树。
给你一棵包含
n个节点的树,标记为0到n - 1。给定数字n和一个有n - 1条无向边的edges列表(每一个边都是一对标签),其中edges[i] = [ai, bi]表示树中节点ai和bi之间存在一条无向边。可选择树中任何一个节点作为根。当选择节点
x作为根节点时,设结果树的高度为h。在所有可能的树中,具有最小高度的树(即,min(h))被称为 最小高度树 。请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。
树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。
示例:
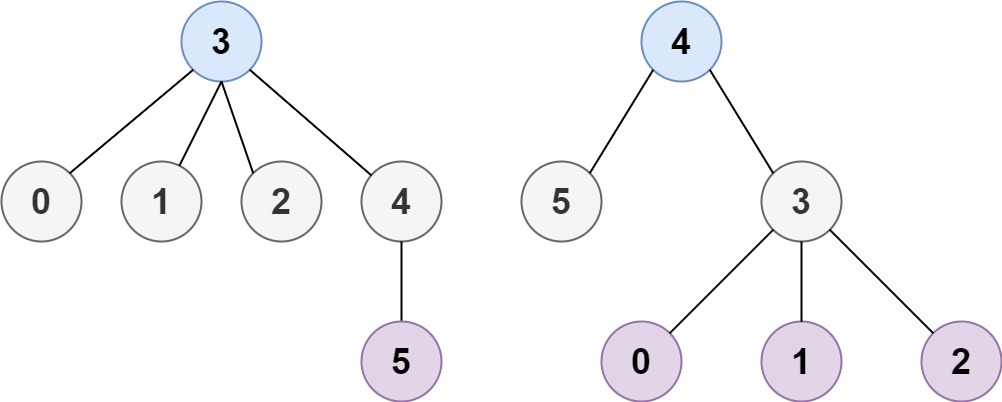
输入:n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]] 输出:[3,4]
解题思路: 本题思路较为复杂,可以大致理解为贪心,证明过程可以参考力扣官方答案。每次去掉节点入度最小的节点,到最后剩余1-2个节点即为可以作为最小高度树的根节点
class Solution {
public:vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {if (n == 1) return {0};unordered_map<int, vector<int>> g;vector<int> degree(n);for (auto& e : edges) {int x = e[0], y = e[1];g[x].push_back(y);g[y].push_back(x);degree[x]++;degree[y]++;} vector<int> ans;queue<int> q;for (int i = 0; i < n; i++) if (degree[i] == 1) q.push(i);while(!q.empty()) {vector<int> tmp;int size = q.size();while(size--) {int x = q.front();q.pop();tmp.push_back(x);for(auto y : g[x]) {if (--degree[y] == 1) q.push(y);}}ans = move(tmp);}return ans;}
};相关文章:
⌈算法进阶⌋图论::拓扑排序(Topological Sorting)——快速理解到熟练运用
目录 一、原理 1. 引例:207.课程表 2. 应用场景 3. 代码思路 二、代码模板 三、练习 1、210.课程表Ⅱ🟢 2、2392.给定条件下构造举证🟡 3、310.最小高度树 🟡 一、原理 1. 引例:207.课程表 就如大学课程安排一样&…...

【Python】【数据结构和算法】保留最后N个元素
使用deque,指定maxlen参数的值为N,例如: >>> from collections import deque >>> dq deque(maxlen3) >>> dq.append(1) >>> dq.append(2) >>> dq.append(3) >>> dq.append(4) >&…...

wireshark 基本使用
在Wireshark中,你可以使用过滤器来根据接口名称定位到特定的包。下面是一些常见的过滤器示例: 根据源或目的IP地址过滤: ip.src 192.168.0.1:过滤源IP地址为192.168.0.1的包。ip.dst 192.168.0.1:过滤目的IP地址为…...

2、结构型设计模式
结构型设计模式 目录 结构型设计模式1. 代理模式1.1 概述1.2 结构1.3 静态代理1)抽象主题类 SellTickets2)真实主题类 TrainStation3)代理类 ProxyPoint4)客户端类1.4 JDK 动态代理1)代理工厂类:ProxyFactory2)客户端类3)JDK 动态代理原理4)动态代理的执行流程是什么样…...
JavaScript下载excel文件
文章目录 通过链接下载a标签下载方法注意 获取文件流请求体配置下载文件流 总结 通过链接下载 a标签 对于已知地址的目标文件,前端可以使用 a标签 来直接下载,使用a标签下载使用到两个属性 download:下载文件名href:目标文件下…...

研磨设计模式day12命令模式
目录 定义 几个参数 场景描述 代码示例 参数化设置 命令模式的优点 本质 何时选用 定义 几个参数 Command:定义命令的接口。 ConcreteCommand:命令接口的实现对象。但不是真正实现,是通过接收者的功能来完成命令要执行的操作 Receiver&#x…...

设计模式 06 适配器模式
适配器模式(Adapter Pattern)属于结构型模式 概述 结构型模式关注如何将现有的类或对象组织在一起形成更加强大的结构。 在生活中,我们经常遇到这样的一个问题:轻薄笔记本通常只有 type-c 或者 usb-a 接口,没有网口。…...
UE4/5Niagara粒子特效之Niagara_Particles官方案例:3.3->4.3
目录 3.3 Visibility Tag 左边的发射器: 发射器更新 粒子生成 粒子更新 右边的发射器 和左边发射器不同的地方 3.4 Texture Sampling 发射器更新 粒子生成 粒子更新 4.1Play Audio Per Particle 系统 第三个发射器 发射器更新 粒子生成 粒子更新 第二个…...
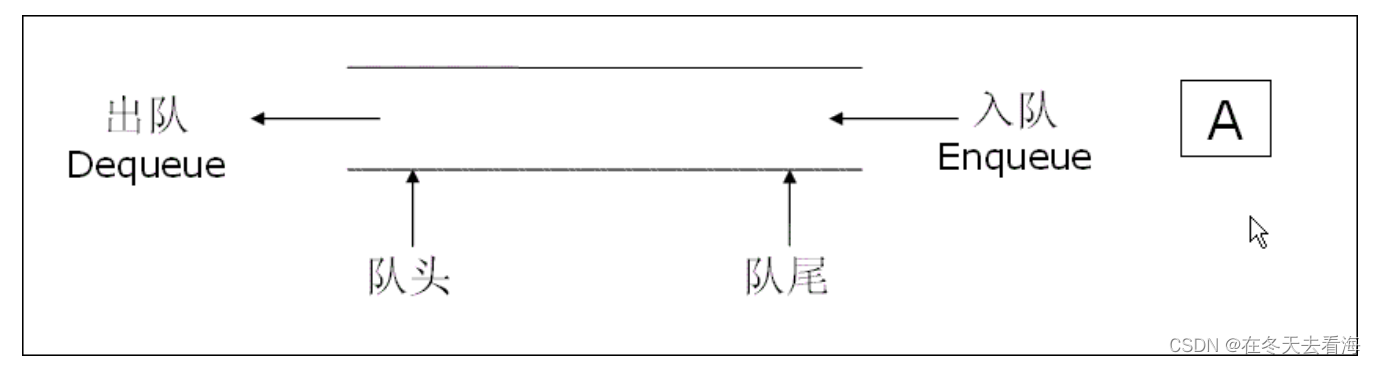
数据结构队列的实现
本章介绍数据结构队列的内容,我们会从队列的定义以及使用和OJ题来了解队列,话不多说,我们来实现吧 队列 1。队列的概念及结构 队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,…...

Gti的基本介绍和使用方式
Git 是一种分布式版本控制系统, 主要用于管理软件开发过程中的代码变更。其基本概念包括: 仓库 (Repository): Git中存储代码的基本单位,即一个代码库。在仓库中可以存储多个分支、标签、提交记录等。 分支 (Branch): Git中的分支是代码的不同开发方向,…...

剑指Offer 24-反转链表
题目描述:定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。 示例: 输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL 解题思路: 这道题做过很多次,还是会…...
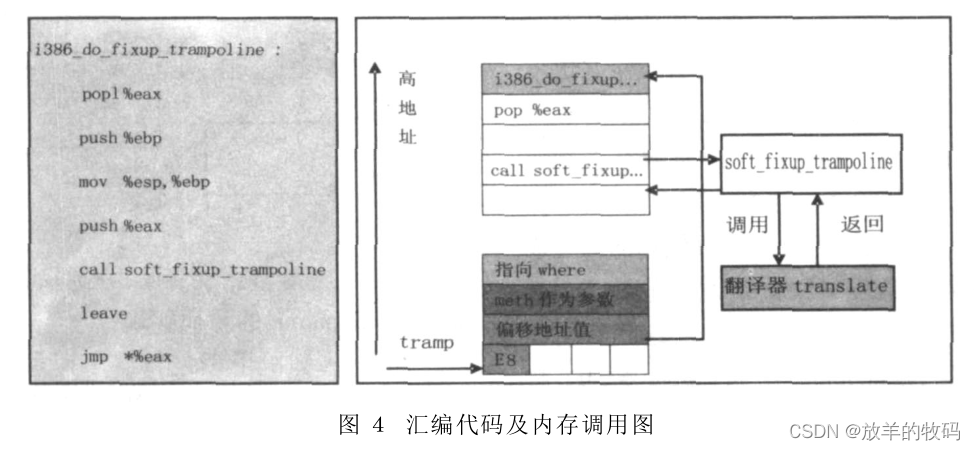
小研究 - Java虚拟机即时编译器的一种实现原理
深入分析了 Kaffe虚拟机的 JIT(Just-In-Ti…...

【LeetCode】416.分割等和子集
题目 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 示例 1: 输入:nums [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] 和 [11] 。 示…...
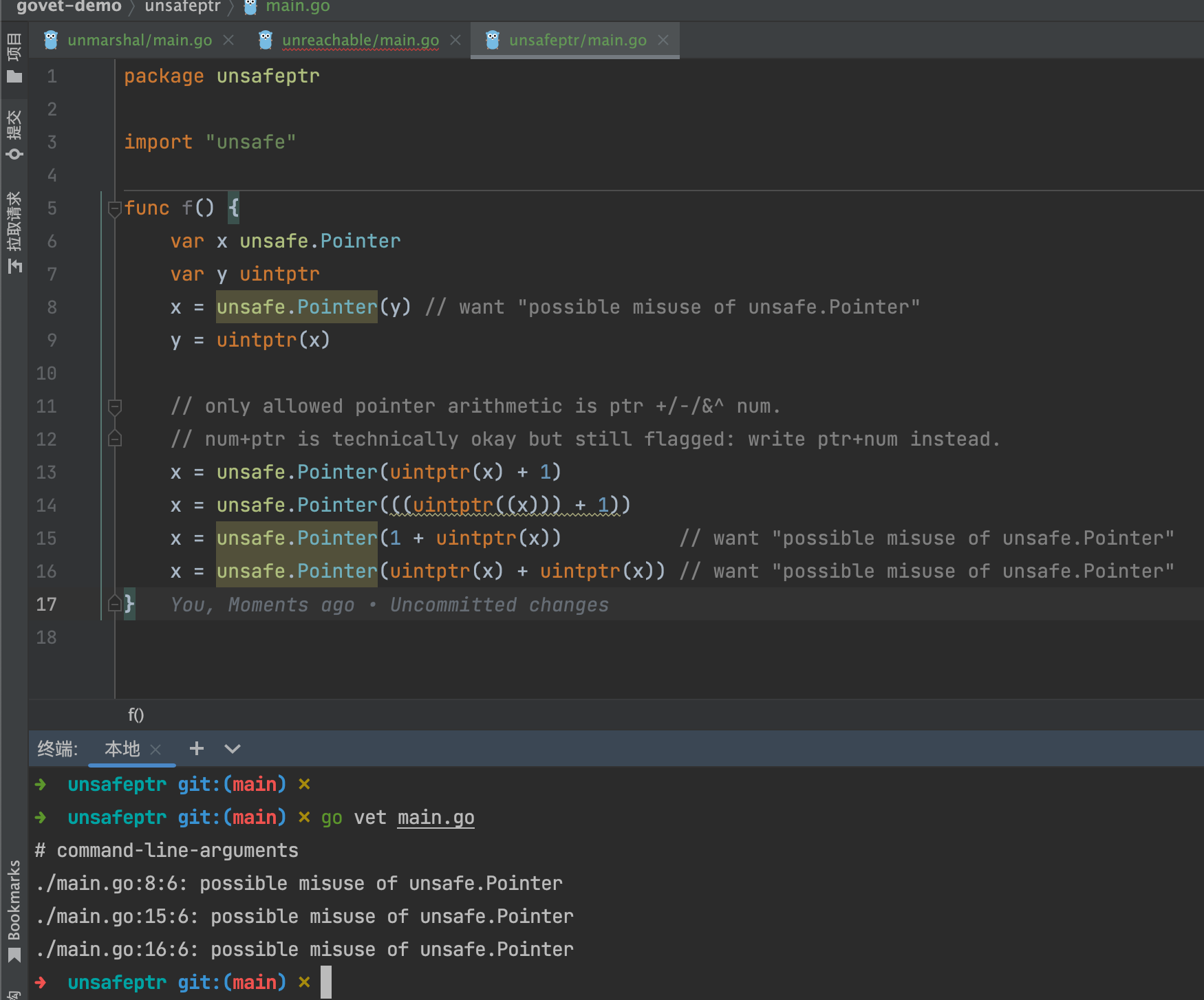
go vet中的那些检测项
go vet 是 Go 语言自带的一个工具,用于分析 Go 代码中的常见错误和潜在问题。它可以检查代码中可能存在的各种问题,例如: 未使用的变量、函数或包 可疑的函数调用 错误的函数签名 程序中的竞态条件 错误的类型转换等 本文意图指令当前go vet所…...

Qt 自定义菜单、右键菜单
在接触Qt这段时间以来,经常遇到菜单项的问题(右键菜单、托盘菜单、按钮菜单等),QMenu用于菜单栏,上下文菜单,弹出菜单等,利用QMenuQAction就可以达到效果! 右键菜单实现:通过重写contextMenuEv…...
VScode 编辑器报错: ‘HelloWorld‘ is declared but its value is never read.
.vue文件被标识红色波浪线;提示: HelloWorld is declared but its value is never read. 问题原因: 因为vue3已经不支持vetur插件。 1、在扩展里面进行搜索Vetur插件,进行禁用或卸载; 2、在 VScode扩展里面搜索并下载…...

如何使用LLM实现文本自动生成视频
推荐:使用 NSDT场景编辑器 助你快速搭建可二次编辑的3D应用场景 介绍 基于扩散的图像生成模型代表了计算机视觉领域的革命性突破。这些进步由Imagen,DallE和MidJourney等模型开创,展示了文本条件图像生成的卓越功能。有关这些模型内部工作的…...

Rust处理JSON
基本操作 Cargo.toml: [package]name "json"version "0.1.0"edition "2021"# See more keys and their definitions at https://doc.rust-lang.org/cargo/reference/manifest.html[dependencies]serde { version "1", features …...

Python如何操作网络爬虫
Python是一种非常强大的编程语言,用于网络爬虫操作也非常方便。Python提供了许多用于构建和操作网络爬虫的库和工具,如BeautifulSoup、Scrapy、Requests等。本文将详细介绍Python如何操作网络爬虫。 一、安装相关库 首先,我们需要安装Python…...

linux文件复制覆盖命令
目录 cp 命令参数2.cp -rf 出现复制不覆盖文件问题3.解决文件复制覆盖提示操作问题,以下四种方式,供大家参考使用。方法1:编写带cp的路径复制覆盖文件方法2:在CP命令前面加一个斜杠\,实现强制覆盖文件方法3:…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...