算法通过村第三关-数组黄金笔记|数组难解
文章目录
- 前言
- 数组中出现超过一半的数字
- 数组中只出现一次的数字
- 颜色的分类问题(荷兰国旗问题)
- 基于冒泡排序的双指针(快慢指针)
- 基于快排的双指针(对撞指针)
- 总结
前言
提示:苦不来自外在环境中的人、事、物,只是自内的妄想和执着。 --金惟纯
这里整理一些比较经典的题目,巩固一下数组的学习。
数组中出现超过一半的数字
题目介绍参考:剑指 Offer 39. 数组中出现次数超过一半的数字 - 力扣(LeetCode)
对于这种题目,如果没有思路的话,我们可以先把常见的数据结构和算法策略过一般,这里参考以前的文章巩固一下。算法通关村第一关-链表白银挑战笔记|公共子节点_师晓峰的博客-CSDN博客

我们想一下,查找统计出所有出现的个数,大于一半就可以,这不就是一种想法🥰,排序行不行呢,对数组进行排序,超过一半必定是中位数。
如果不了解中位数这个概念的:
🐟聪明回答:
在数学中,中位数指的是一组数字排序后的中间值,即将一组数字从小到大排列,中间的那个数就是中位数。如果一组数字有奇数个,那么中位数就是排序后的中间数;如果一组数字有偶数个,那么中位数是中间两个数的平均值。中位数可以用来表示一组数据的中心趋势,较为稳定而不易受极端值的影响。
但是如果你不放心的话可以在遍历一遍数组,确定这个数组是否超过一半,所以第二种方法就出来了。这种方法的时间复杂度取决于排序算法的时间复杂度,最快的话O(nlogn),排序的代价比较高,我们试想一下还有别的方法吗💡
我们使用Hash行不行呢?我们先创建一个HashMap的key是元素的值,value是已经出现的次数,然后遍历数组来统计所有元素出现的次数,最后在遍历一边Hash,找到次数超过一半的数字,这不又一种方法出来了。
我们展示一下代码:
/*** 方法1 基于Hash* @param array* @return*/public static int moreThanHalfNum(int[] array) {// 参数校验if (array == null || array.length == 0) {return 0;}HashMap<Integer, Integer> res = new HashMap<>();int len = array.length;for (int i = 0; i < len; i++) {res.put(array[i], res.getOrDefault(array[i], 0) + 1);if (res.get(array[i]) > len / 2){return array[i];}}return 0;}
当然采用Hash的方法可以解决,但是这里最多给70,着并不是最优的结果,那么有没有巧妙的方法呢?
拓展:采用上面你的算法时间复杂度为O(n),但是这是用空间复杂度O(n)换来的,那么有没有空间复杂度为O(1)且时间负责度为O(n)的呢?💡
你听说过摩尔投票法则吗?它用来解决多数问题(中位数)可以说是一把利刃。
🐟聪明的回答:
摩尔投票法(Moore’s Voting Algorithm)是一种用于在数组或列表中查找出现次数超过一半的元素的算法。该算法基于以下观察:如果一个元素出现次数超过一半,那么它在数列中出现的次数一定比其他所有元素出现次数之和还要多。
算法步骤如下:
- 初始化两个变量:候选元素(candidate)和计数器(count),候选元素用于保存当前被选中的元素,计数器用于统计候选元素的出现次数。
- 遍历整个数组或列表,对于每一个元素:
- 如果计数器为0,将当前元素设为候选元素,将计数器设为1。
- 否则,如果当前元素与候选元素相同,计数器加1;否则,计数器减1。
- 完成遍历后,最后留下的候选元素就是候选元素,但这并不代表它一定是超过一半的元素,只是候选元素的可能性更高。
- 最后,再次遍历整个数组或列表,统计候选元素的出现次数。如果它的出现次数确实超过一半,那么它就是超过一半的元素;否则,不存在超过一半的元素。
下面给出一个例子来解释摩尔投票法:
假设我们有一个数组:[2, 4, 5, 2, 2]。
- 遍历第一个元素2,将其设为候选元素,计数器为1。
- 遍历第二个元素4,与候选元素不同,计数器减1。
- 遍历第三个元素5,与候选元素不同,计数器减1。
- 遍历第四个元素2,与候选元素相同,计数器加1。
- 遍历第五个元素2,与候选元素相同,计数器加1。
此时,计数器为2,最后剩下的候选元素是2。
再次遍历整个数组,统计元素2的出现次数,发现它出现了3次,大于数组长度的一半,所以2就是超过一半的元素。
/*** 方法二:比较特殊的计数法** @param array* @return*/public static int moreThanHalfNum2(int[] array) {if (array == null || array.length == 0) {return 0;}int count = 0;Integer candidate = null;for (int num : array) {if (count == 0) {candidate = num;}count += (num == candidate) ? 1 : -1;}// check 记得在检查一边count = 0;int len = array.length;for (int num : array) {if (num == candidate) {count++;}if (count >= len / 2) {return candidate;}}return candidate;}
Q&A
Q : 这里问什么要在检查一边,可以不检查?会出现什么问题?
A :必须再检查一边,这里是确保candidate一定是超出一半的数,不检查投出的结果不一定正确[1,2,3],有结果,但是不符合要求。
数组中只出现一次的数字
参考题目介绍:136. 只出现一次的数字 - 力扣(LeetCode)

这个题用Set集合解决比较好,Set集合不存储重复元素,这个是该集合的特性。题目说明其他元素都是出现两次,我们刚好可以利用这个操作,当要添加元素的key与集合中已存在的数出现重复的时候,我们就不进行操作,并且将这个key一起删掉,确保只存在一个数,这样遍历一边就可以知道答案了。【注意:确保集合有元素 】
/*** 基于集合寻找** @param arr* @return*/public static Integer findOneNum(int[] arr) {// 校验参数if (arr == null || arr.length == 0){return null;}// 特殊处理if (arr.length == 1) {return arr[0];}HashSet<Integer> res = new HashSet<>();for(int i = 0; i < arr.length; i++){if (!res.add(arr[i])){res.remove(arr[i]);}}// check 确保set集合存在元素if (res.size() == 0){return null;}return (Integer) res.toArray()[0];}
当然这个方法也不是最优解,算法就是这么奇妙,有时后令人讨厌,有时候让你欣喜。提示一下,可以想一想位运算来解决:你知道异或这个操作吗?
🐟聪明回答:
计算机中的异或操作(XOR),也称为“排他性或”操作,是一种逻辑运算,用于比较两个值的不同之处。异或操作有以下几条规则:
- 同一个值与自身进行异或操作结果为0:A ⊕ A = 0
- 任意值与0进行异或操作结果不变:A ⊕ 0 = A
- 异或操作满足交换律:A ⊕ B = B ⊕ A
- 异或操作满足结合律:(A ⊕ B) ⊕ C = A ⊕ (B ⊕ C)
- 异或操作满足自反性:A ⊕ B ⊕ A = B
举例来说明:
- 与自身进行异或操作:7 ⊕ 7 = 0
- 与0进行异或操作:5 ⊕ 0 = 5
- 交换律:3 ⊕ 5 = 5 ⊕ 3
- 结合律:(2 ⊕ 4) ⊕ 6 = 2 ⊕ (4 ⊕ 6)
- 自反性:2 ⊕ 4 ⊕ 2 = 4
异或操作在计算机中有很多应用,其中一个常见的应用是用于交换两个变量的值。例如,假设有两个变量a和b,我们可以使用异或操作进行交换如下:
a = a ⊕ b;
b = a ⊕ b;
a = a ⊕ b;
在经过以上操作后,a和b的值就被交换了。
看到了吗?我们可以根据这个自反性质得到我们想要的答案,是不是非常简单😁。
遍历一边就能拿到想要的结果,代码展示:
/*** 基于位运算* 0 ^ * = ** A ^ B ^ A = B* @param arr* @return*/public static int findOneNum2(int[] arr) {int res = 0;for(int num : arr){res ^= num;}return res;}
颜色的分类问题(荷兰国旗问题)
参考题目介绍:75. 颜色分类 - 力扣(LeetCode)

那我们就来认识一下荷兰的国旗吧:

感兴趣的可以看看历史:荷兰和俄罗斯的国旗为什么高度相似?到底是谁抄袭谁? (baidu.com)
这个问题很典型,双指针问题,当然可以采用多种方式的双指针解决,我们研究第一种与冒泡类似的,第二种与快排类似。
基于冒泡排序的双指针(快慢指针)
冒泡排序我们都知道,就是根据大小逐步和后面的比较,慢慢调整到整体有序的状态,这种方法是比较稳定的排序方法。
当然我们可以这样考虑:
- 第一次遍历,我们将数组中所有0交换到数组的头部
- 第二次遍历,只需要处理1和2。
漂亮的双指针代码如下:
public static void sortColors(int[] nums) {// 定义快慢指针int n = nums.length;int left = 0;// 先处理 0 把0移到最左边for(int right = 0; right < n; right++) {if (nums[right] == 0){swap(nums,left,right);left++;}}// 接着处理1 把1移到次走遍for(int right = left; right < n; right++){if (nums[right] == 1){swap(nums,left,right);left++;}}}// 采用位运算的方式交换public static void swap(int[] nums, int left, int right) {nums[left] = nums[left] ^ nums[right];nums[right] = nums[left] ^ nums[right];nums[left] = nums[left] ^ nums[right];}
这里解决的话效果还是可以的,但是如果再进一步问你,可以一次遍历就解决吗?你就要考虑第二种方法了。
基于快排的双指针(对撞指针)
如果要求一次遍历就解决问题,我们要怎么想办法呢?隐约觉得需要使用三个指针才可以:
- left指针,表示left左侧的元素都是0
- right指针,便是right右侧的元素都是2
- index指针,从头到尾遍历数组,根据nums[index]是0还是2决定与left交换还是和right交换
index的位置上的元素代表我们将要处理的数字。index为1,我们不需要做什么,直接+ 1,如果是0,放在左边,如果是2,放在右边,当index == right的时候就可以停止了。
我们画图表示一下:
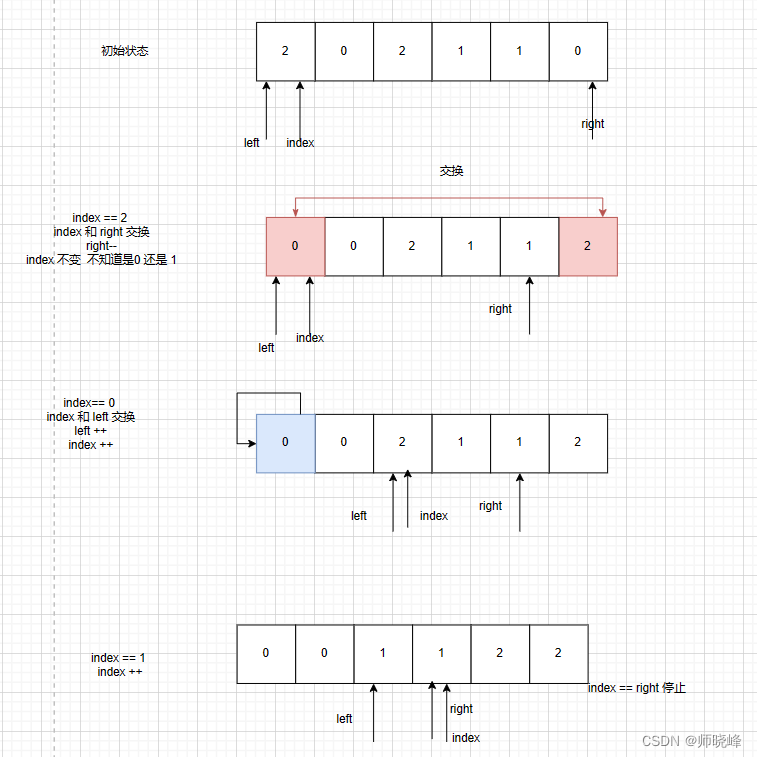
这里面的重点在于index的位置为2的时候进行交换后为right–,index不做处理,当然这里考虑到了,index 为 1的情况,所以先不动,1 比较特殊,跳过去就没法处理了。
那么问题来了,index 为0的时候执行交换的话index++,如果存在都会被交换到右边,这里只需要处理1和0的问题就可以了。
代码如下:
/*** 采用位运算的方式交换* @param nums* @param left* @param right*/public static void swap(int[] nums, int left, int right) {nums[left] = nums[left] ^ nums[right];nums[right] = nums[left] ^ nums[right];nums[left] = nums[left] ^ nums[right];}public static void sortColors(int[] nums) {// 定义快慢指针int left = 0 , index = 0,right = nums.length - 1;while(index <= right) {if (nums[index] == 2){swap(nums,index,right--);}else if (nums[index] == 0){swap(nums,index++,left++);}else {index++;}}}
总结
注意:双指针问题,边界和条件。
相关文章:

算法通过村第三关-数组黄金笔记|数组难解
文章目录 前言数组中出现超过一半的数字数组中只出现一次的数字颜色的分类问题(荷兰国旗问题)基于冒泡排序的双指针(快慢指针)基于快排的双指针(对撞指针) 总结 前言 提示:苦不来自外在环境中的人、事、物,…...

【2023】LeetCode HOT 100——矩阵
目录 1. 矩阵置零1.1 C++实现1.2 Python实现1.3 时空分析2. 螺旋矩阵2.1 C++实现2.2 Python实现2.3 时空分析3. 旋转图像3.1 C++实现3.2 Python实现3.3 时空分析4. 搜索二维矩阵 II4.1 C++实现4.2 Python实现4.3 时空分析1. 矩阵置零 🔗 原题链接:...
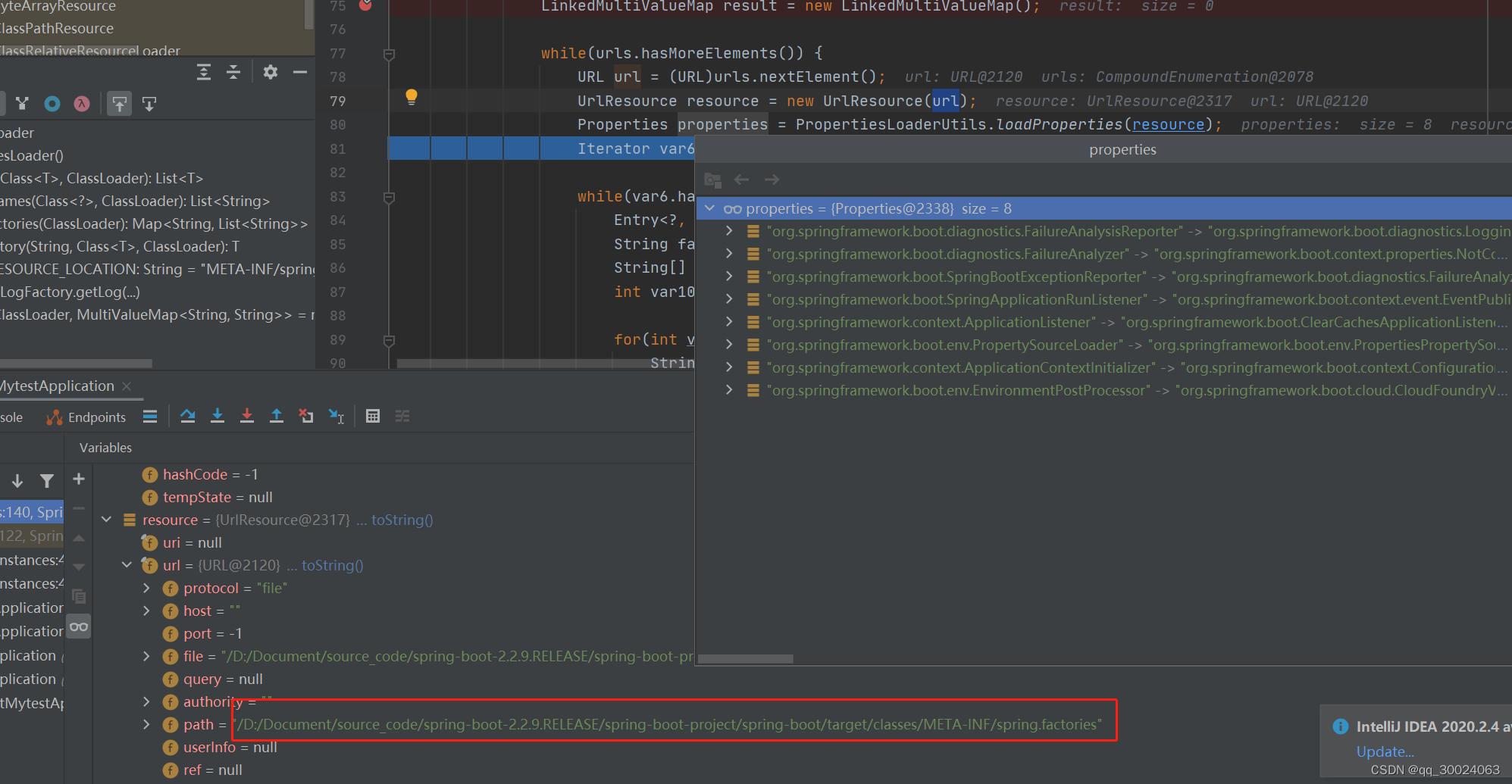
springboot源码方法
利用LinkedHashSet移除List重复的数据protected final <T> List<T> removeDuplicates(List<T> list) {return new ArrayList<>(new LinkedHashSet<>(list));} SpringFactoriesLoader#loadFactoryNames 加载配置文件...

基于java街球社区网站设计与实现
摘 要 本文主要讲述了基于SpringBootVue模式的街球社区网站的设计与实现。这里所谓的街球社区网站是通过类似于百度贴吧之类的网上论坛使得所有的街球爱好者有一个可以互相交流的平台,并使所有用户可以在社区进行教学视频的观看以及相关体育运动产品的选购,平台的盈利主要靠…...

定时产生不同频率方波
/*----------------------------------------------- 内容:通过定时产生不同频率方波 ------------------------------------------------*/ #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存器的定义 /*-…...
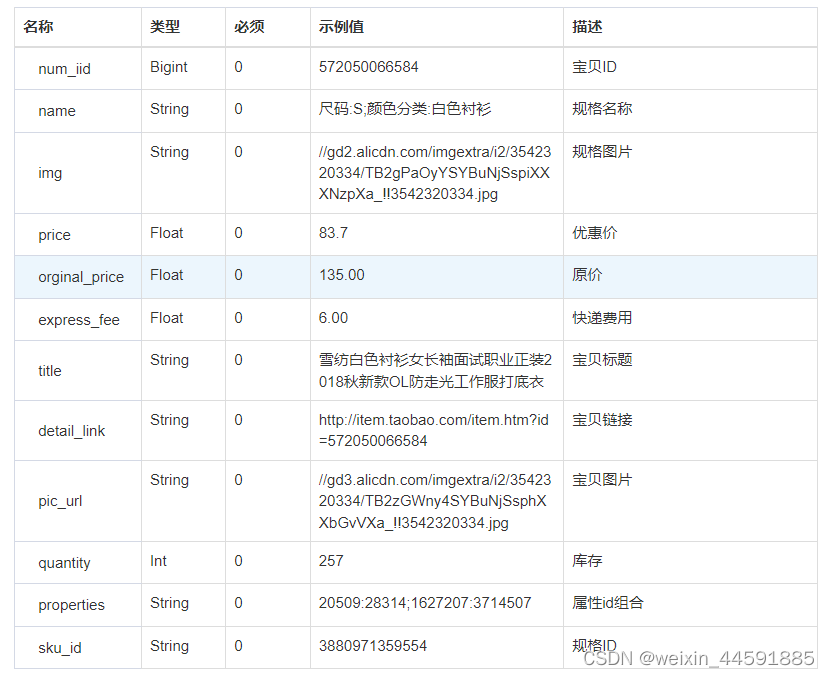
Java“牵手”天猫商品sku信息API接口数据,天猫API接口申请指南
天猫平台商品sku属性信息接口是开放平台提供的一种API接口,通过调用API接口,开发者可以获取天猫商品的标题、价格、库存、月销量、总销量、库存、详情描述、图片等详细信息 。 获取商品销量接口API是一种用于获取电商平台上商品sku属性数据的接口&#…...
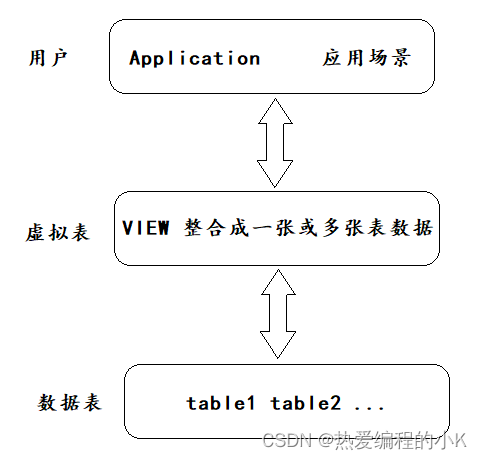
【⑮MySQL | 视图】概述 | 创建 | 查看 | 更新 | 修改 | 删除
前言 ✨欢迎来到小K的MySQL专栏,本节将为大家带来MySQL视图概述 | 创建 | 查看 | 更新 | 修改 | 删除的分享✨ 目录 前言1.视图概述2.创建视图3.查看视图4.更新视图数据5.修改视图6.删除视图总结 1.视图概述 1.1 为什么使用视图? 视图一方面可以帮我们使…...

Linux驱动开发一、RK3568把hello编译到Linux内核中运行。‘rk_vendor_read’未定义的引用
1、在字符设备目录下建立hello目录 ~/Linux/rk356x_linux/kernel/drivers/char/hello 2、进入hello目录,新建hello.c、Makefile、Kconfig三个文件 3、Kconfig是打开make menuconfig配置界面是后的选项,这Kconfig是在字符设备下的。 config HELLOtrist…...

enable_shared_from_this
用途: enable_shared_from_this 是一个基类模板,用于解决在类成员函数中获取类对象的 shared_ptr 的需求。它提供了一种机制,使类能够安全地从成员函数内部获得指向自身的 shared_ptr。 解决对象生命周期管理问题:在某些情况下&…...
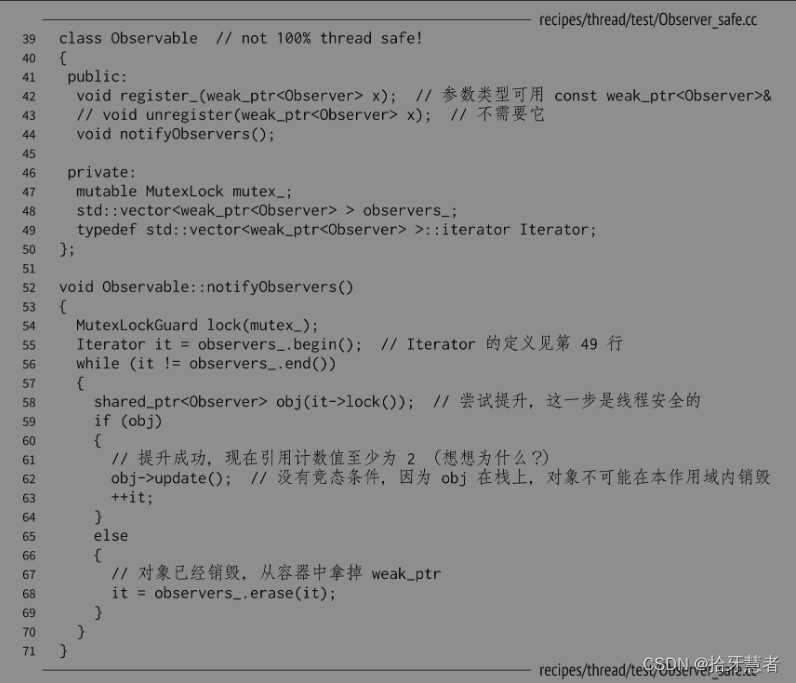
weak_ptr是怎么探知对象生死的
weak_ptr是C智能指针中的一种。它用于解决共享所有权的问题,并且可以避免因循环引用而导致的内存泄漏。 weak_ptr本身并不承担对象的所有权,它指向由shared_ptr管理的对象。与shared_ptr不同,weak_ptr并不会增加计数器来计算对象的引用次数。…...
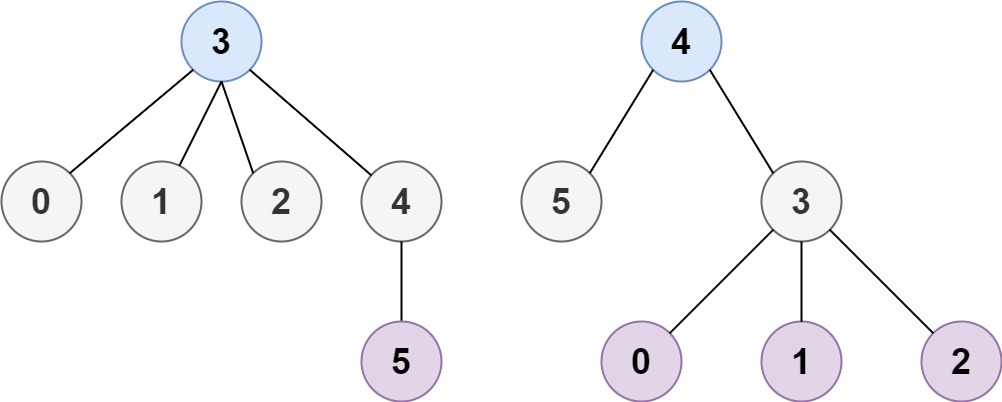
⌈算法进阶⌋图论::拓扑排序(Topological Sorting)——快速理解到熟练运用
目录 一、原理 1. 引例:207.课程表 2. 应用场景 3. 代码思路 二、代码模板 三、练习 1、210.课程表Ⅱ🟢 2、2392.给定条件下构造举证🟡 3、310.最小高度树 🟡 一、原理 1. 引例:207.课程表 就如大学课程安排一样&…...

【Python】【数据结构和算法】保留最后N个元素
使用deque,指定maxlen参数的值为N,例如: >>> from collections import deque >>> dq deque(maxlen3) >>> dq.append(1) >>> dq.append(2) >>> dq.append(3) >>> dq.append(4) >&…...

wireshark 基本使用
在Wireshark中,你可以使用过滤器来根据接口名称定位到特定的包。下面是一些常见的过滤器示例: 根据源或目的IP地址过滤: ip.src 192.168.0.1:过滤源IP地址为192.168.0.1的包。ip.dst 192.168.0.1:过滤目的IP地址为…...

2、结构型设计模式
结构型设计模式 目录 结构型设计模式1. 代理模式1.1 概述1.2 结构1.3 静态代理1)抽象主题类 SellTickets2)真实主题类 TrainStation3)代理类 ProxyPoint4)客户端类1.4 JDK 动态代理1)代理工厂类:ProxyFactory2)客户端类3)JDK 动态代理原理4)动态代理的执行流程是什么样…...
JavaScript下载excel文件
文章目录 通过链接下载a标签下载方法注意 获取文件流请求体配置下载文件流 总结 通过链接下载 a标签 对于已知地址的目标文件,前端可以使用 a标签 来直接下载,使用a标签下载使用到两个属性 download:下载文件名href:目标文件下…...

研磨设计模式day12命令模式
目录 定义 几个参数 场景描述 代码示例 参数化设置 命令模式的优点 本质 何时选用 定义 几个参数 Command:定义命令的接口。 ConcreteCommand:命令接口的实现对象。但不是真正实现,是通过接收者的功能来完成命令要执行的操作 Receiver&#x…...

设计模式 06 适配器模式
适配器模式(Adapter Pattern)属于结构型模式 概述 结构型模式关注如何将现有的类或对象组织在一起形成更加强大的结构。 在生活中,我们经常遇到这样的一个问题:轻薄笔记本通常只有 type-c 或者 usb-a 接口,没有网口。…...
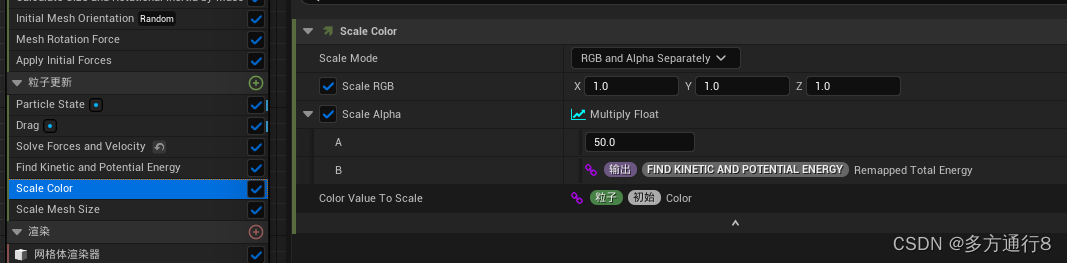
UE4/5Niagara粒子特效之Niagara_Particles官方案例:3.3->4.3
目录 3.3 Visibility Tag 左边的发射器: 发射器更新 粒子生成 粒子更新 右边的发射器 和左边发射器不同的地方 3.4 Texture Sampling 发射器更新 粒子生成 粒子更新 4.1Play Audio Per Particle 系统 第三个发射器 发射器更新 粒子生成 粒子更新 第二个…...
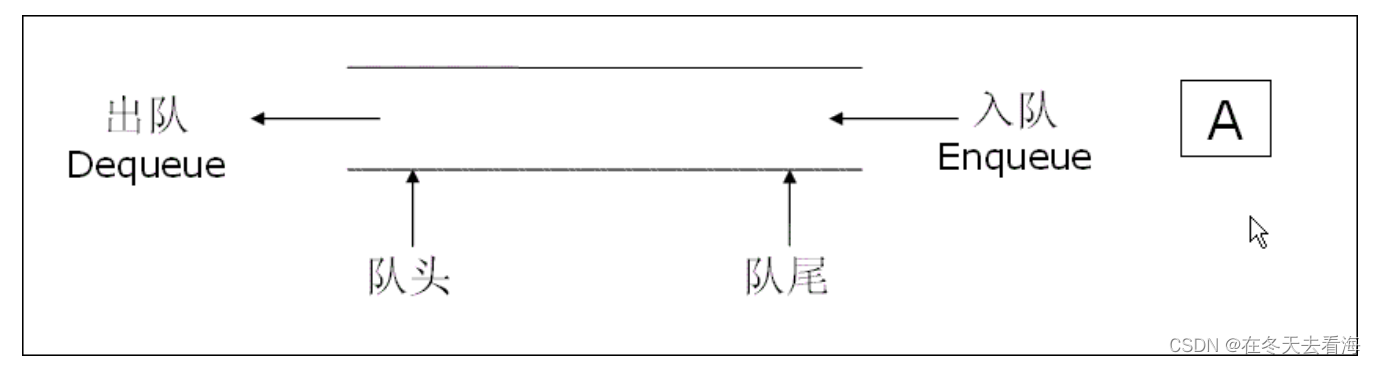
数据结构队列的实现
本章介绍数据结构队列的内容,我们会从队列的定义以及使用和OJ题来了解队列,话不多说,我们来实现吧 队列 1。队列的概念及结构 队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,…...

Gti的基本介绍和使用方式
Git 是一种分布式版本控制系统, 主要用于管理软件开发过程中的代码变更。其基本概念包括: 仓库 (Repository): Git中存储代码的基本单位,即一个代码库。在仓库中可以存储多个分支、标签、提交记录等。 分支 (Branch): Git中的分支是代码的不同开发方向,…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
