【基础算法】之 冒泡排序优化
冒泡排序思想
基本思想: 冒泡排序,类似于水中冒泡,较大的数沉下去,较小的数慢慢冒起来(假设从小到大),即为较大的数慢慢往后排,较小的数慢慢往前排。
直观表达,每一趟遍历,将一个最大的数移到序列末尾。
下图演示排序流程:
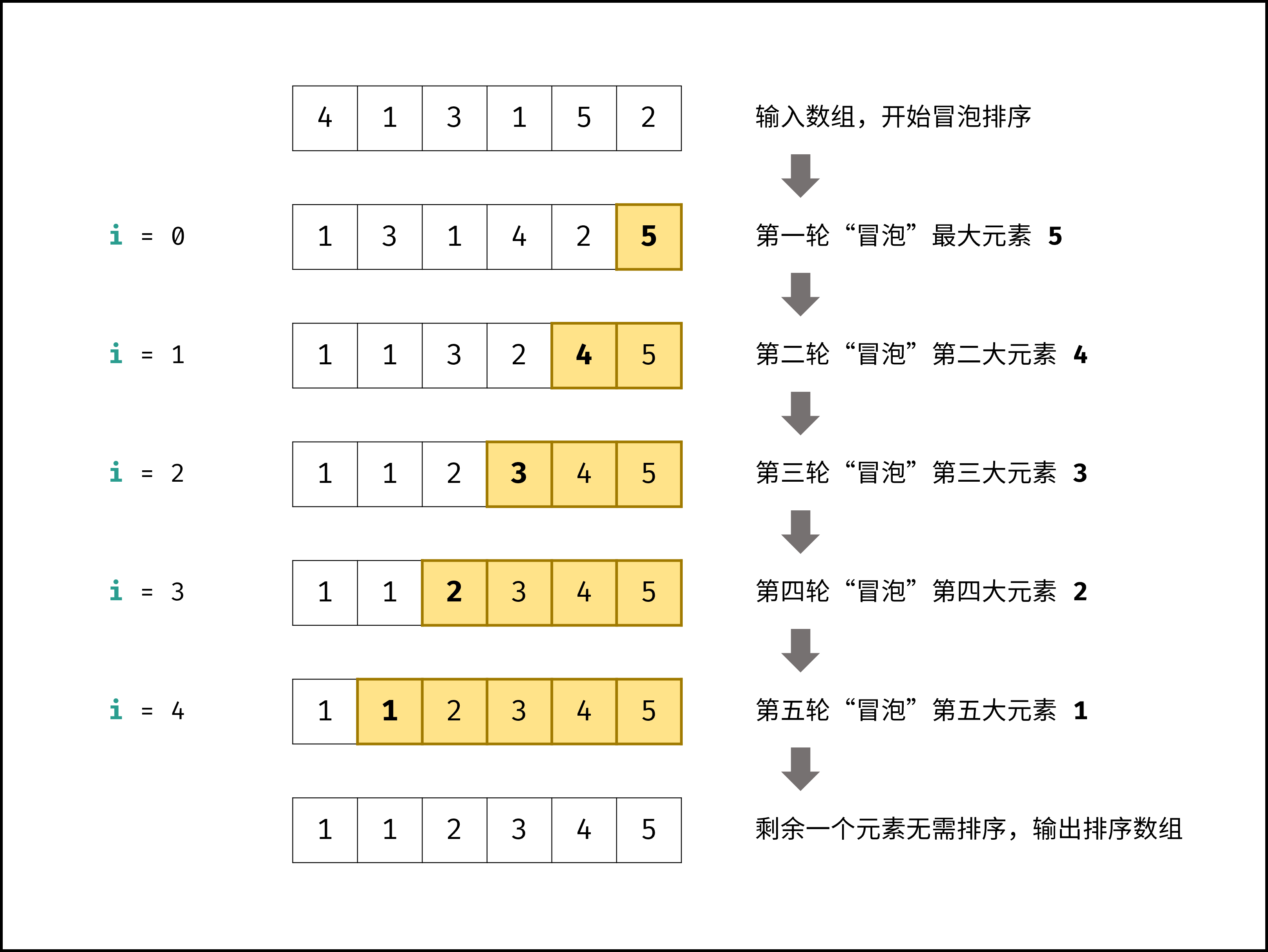
下面是传统冒泡排序写法 时间复杂度O(n^2):
public static void bubbleSort(int[] nums) {int length = nums.length;for (int i = 0; i < length; i++) {System.out.println("i=" + i);for (int j = 0; j + 1 < length -i; j++) {System.out.println("内层循环次数:====================-" + j);if (nums[j] > nums[j + 1]) {int tem = nums[j];nums[j] = nums[j + 1];nums[j + 1] = tem;}}System.out.println("=======第" + i + " 轮外循环执行==============================");for (Integer integer : nums) {System.out.println(integer);}}}执行下看看效果:



第一轮 5次 ,第二轮 4次,第三轮 3次, 第四轮 2次 ,第五轮 1次 ,第六轮0次
但是当我们遇到下面这种序列
即: 1,2,3,5,4 我们只需要排一趟就可以了 而无需后续的循环。
初次优化:
基于这种情况我们给出了下面这种优化。
通过增加一个标志位 flag ,若在某轮「内循环」中未执行任何交换操作,则说明数组已经完成排序,直接返回结果即可。
public static void bubbleSort1(int[] nums) {int length = nums.length;//定义标志位标记已经有序或无序boolean flag = false;for (int i = 0; i < length; i++) {System.out.println("i=" + i);flag = true;for (int j = 0; j + 1 < length - i; j++) {System.out.println("内层循环次数:====================-" + j);if (nums[j] > nums[j + 1]) {int tem = nums[j];nums[j] = nums[j + 1];nums[j + 1] = tem;//交换后对flag置false,表示已经处理成有序flag = false;}}// 已经排好序了 无需后续循环了if (flag) {break;}System.out.println("=======第" + i + " 轮外循环执行==============================");for (Integer integer : nums) {System.out.println(integer);}}}在看下执行效果:

第一轮 5次 ,第二轮 4次,第三轮 3次 ,第四轮 2次
很明显外层减少了循环次数
优化后的冒泡排序的最差和平均时间复杂度仍为 O(N^2) ;在输入数组 已排序 时,达到 最佳时间复杂度 O(N) 。
继续优化:
然而这种优化只能做到某一次已经排好序的时候我们直接跳跳出来,基于第一种优化我们得到一种启发:当一个数组接近有序的时候我们往往只需要在某一个小范围内排序即可,我们可以用一个标记来表示这个范围的下限,例如遇到下面的情况
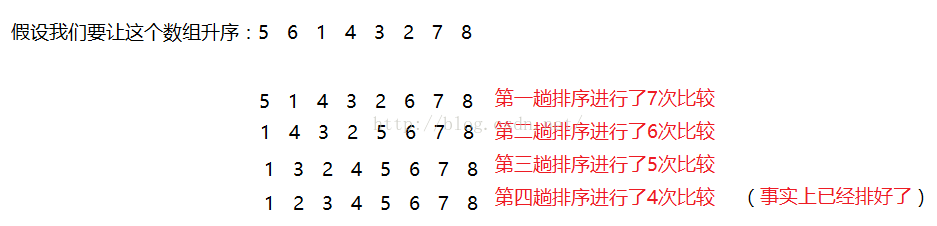
然而我们发现,每次排序前或排序后数组的后面都有一部分已经有序,这时我们只要记下最后一次排下的数组的下标,下次排序的时候就可以只排序到此下标位置即可

目的就是减少内层循环比较的次数
public static void bubbleSort2(int[] nums) {int length = nums.length;int index = length;//每一次我们找到无序区的上界int maxIndex = 0;//定义标志位标记已经有序或无序boolean flag = false;for (int i = 0; i < length; i++) {System.out.println("i=" + i);flag = true;for (int j = 0; j + 1 < index; j++) {System.out.println("内层循环次数:====================-" + j);if (nums[j] > nums[j + 1]) {int tem = nums[j];nums[j] = nums[j + 1];nums[j + 1] = tem;//交换后对flag置false,表示已经处理成有序flag = false;//注意不要在这里直接将index置为jmaxIndex = j + 1;}}// 已经排好序了 无需后续循环了if (flag) {break;}//若排序过则将index置为最后一次交换的坐标,若没有则表示已经有序index = maxIndex;System.out.println("=======第" + i + " 轮外循环执行==============================");for (Integer integer : nums) {System.out.println(integer);}}}再次执行看看效果:


第一轮 5次 ,第二轮 3次,第三轮 2次 ,第四轮 1次
很明显内层循环也减少了很多
优化后的冒泡排序的最差和平均时间复杂度仍为 O(N^2) ;在输入数组 已排序 时,达到 最佳时间复杂度 O(1) 。
其实还可以再优化, 一层外循环 执行2个同级的内循环( 正着扫描得到最大值, 反着扫描得到最小值)
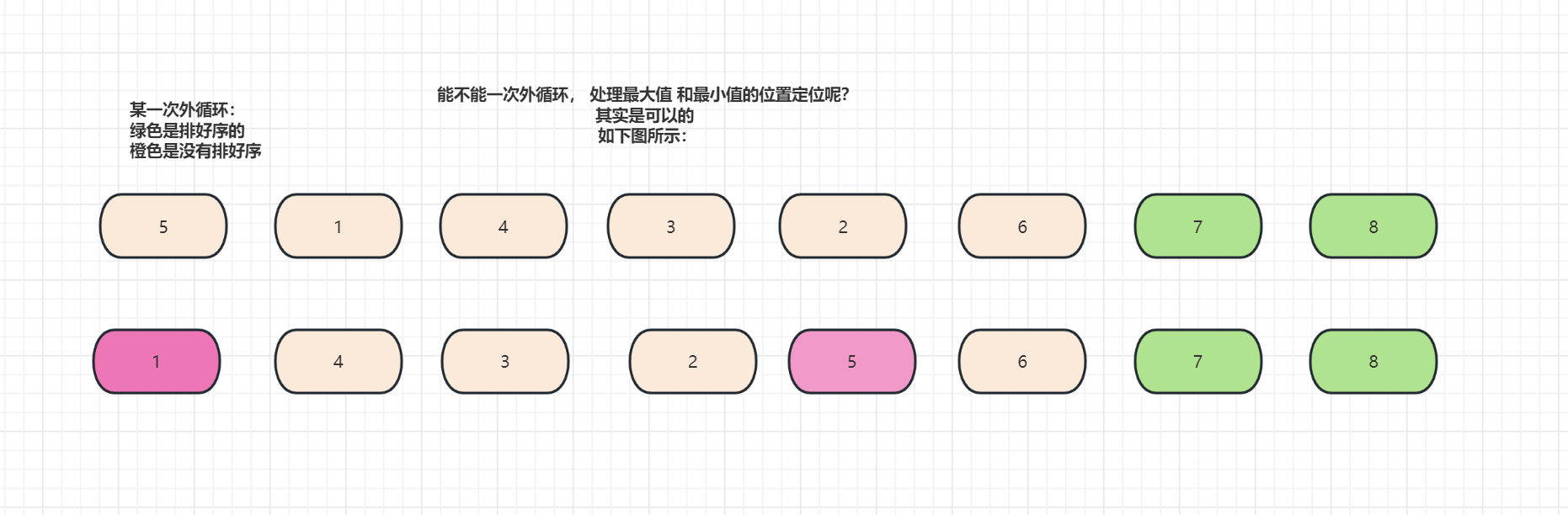
总结
主要从以下2方面优化了传统的冒泡排序写法
// 1、减少外层循环次数
// 2、减少内层循环次数
相关文章:

【基础算法】之 冒泡排序优化
冒泡排序思想基本思想: 冒泡排序,类似于水中冒泡,较大的数沉下去,较小的数慢慢冒起来(假设从小到大),即为较大的数慢慢往后排,较小的数慢慢往前排。直观表达,每一趟遍历,…...
)
Python | 线程锁 | 3分钟掌握【同步锁】(Threading.Lock)
文章目录概念无锁加锁死锁解决死锁概念 threading.Lock 同步锁,可以用于保证多个线程对共享数据的独占访问。 当一个线程获取了锁之后,其他线程在此期间将不能再次获取该锁,直到该线程释放锁。这样就可以保证共享数据的独占访问,…...
Linux下安装MySQL8.0的详细步骤(解压tar.xz安装包方式安装)
Linux下安装MySQL8.0的详细步骤 第一步:下载安装配置 第二步:修改密码,并设置远程连接(为了可以在别的机器下面连接该mysql) 第三步:使用Navicat客户端连接 搞了一台云服务器,首先要干的活就是…...
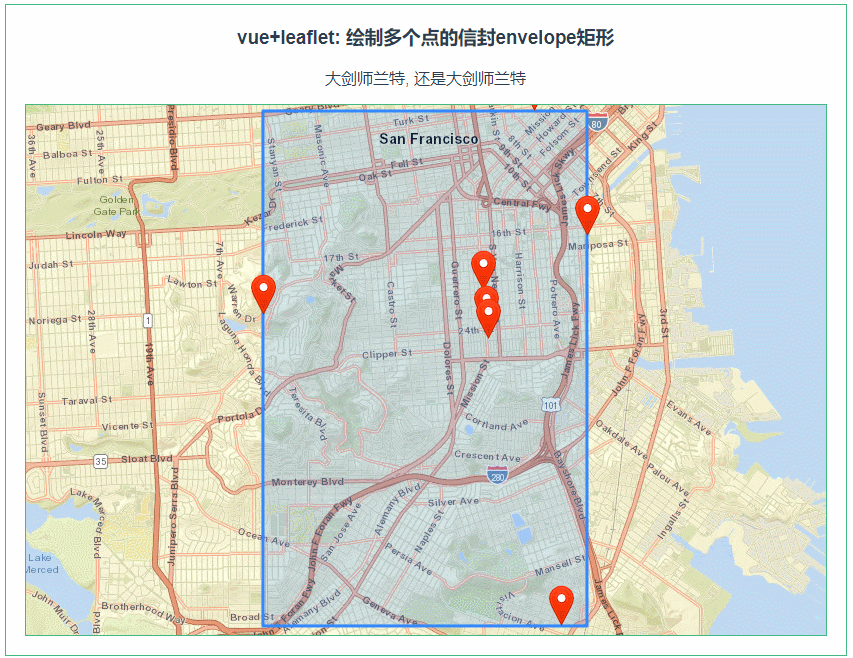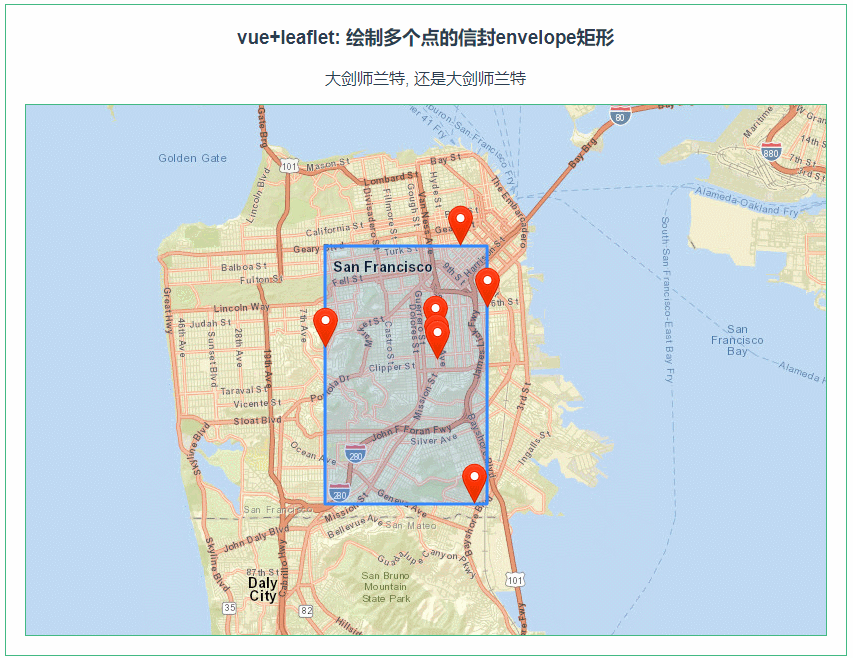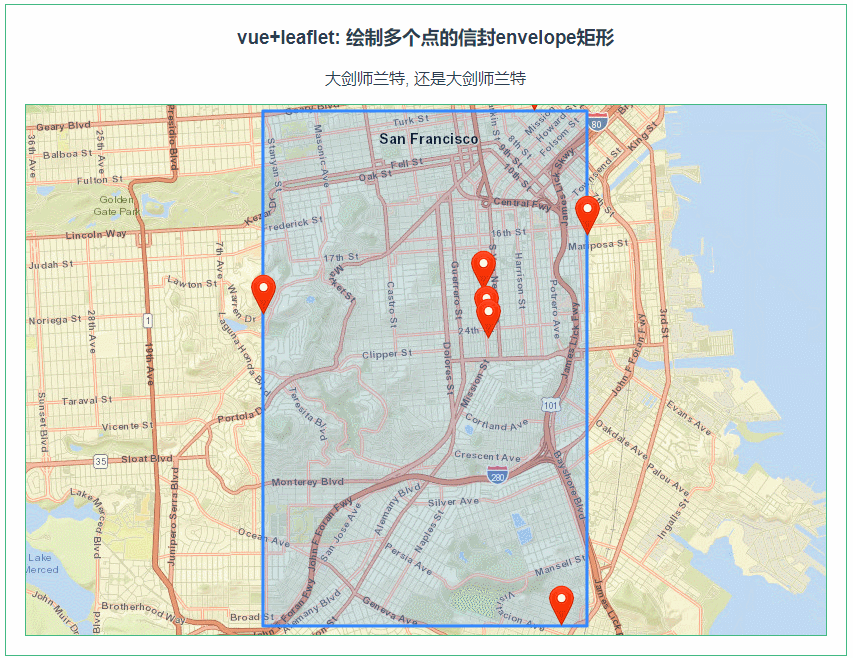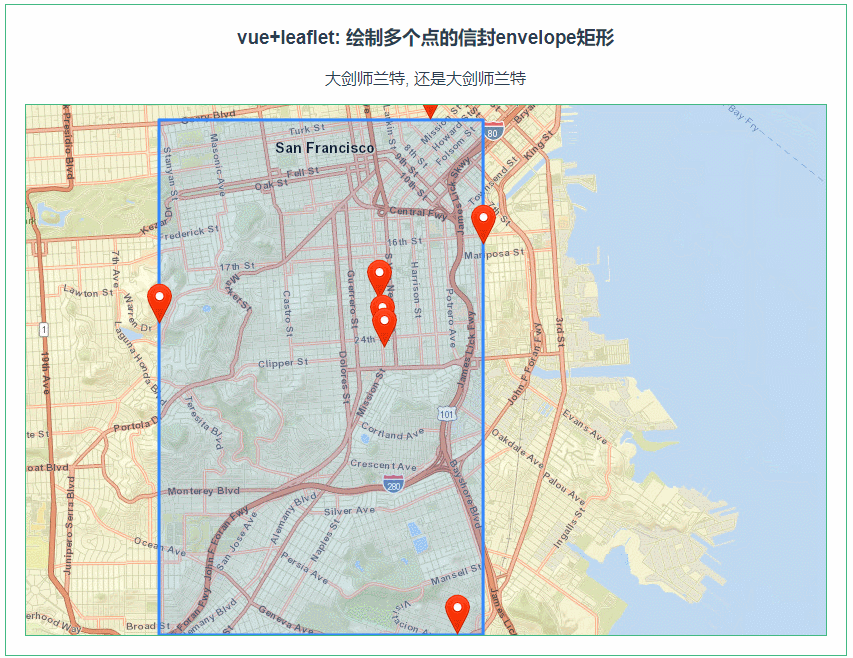
leaflet 绘制多个点的envelope矩形(082)
第082个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中如何根据多边形的几个坐标点来绘制envelope矩形。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果. 文章目录 示例效果配置方式示例源代码(共78行)安装插件相关API参考:专栏目标示例…...
CAJ论文怎么批量免费转换成Word
大家都知道CAJ文件吗?这是中国学术期刊数据库中的文件,这种文件类型比较特殊。如果想要提取其中的内容使用,该如何操作呢?大家可以试试下面这种免费的caj转word的方法,多个文档也可以一起批量转换。准备材料:CAJ文档、…...

面试必问: 结构体大小的计算方法
结构体大小的计算需同时满足以下几点 一、结构体成员的偏移量必须是当前成员大小的整数倍。(0是任何数的整数倍) 举一个例子 struct Test1{char a; // 当前偏移量为0,是char所占字节数1的整数倍 所以所占大小为1char b; …...

Java中super函数的用法
1 问题 Java中super函数有很多方法,在使用的时候我们应该如何正确区分? 2 方法 三种用法: 访问父类的方法。 调用父类构造方法。 访问父类中的隐藏成员变量。 class A{ int x,y; A(int x,int y){ System.out.println("A"); } } cla…...

第十一届“泰迪杯”数据挖掘挑战赛携“十万”大奖火热来袭
第十一届“泰迪杯”数据挖掘挑战赛 竞赛组织 主办单位: 泰迪杯数据挖掘挑战赛组织委员会 承办单位: 广东泰迪智能科技股份有限公司 人民邮电出版社 协办单位: 重庆市工业与应用数学学会、广东省工业与应用数学学会、广西数学学会、河北省工业…...

分享三个可以在家做的正规兼职工作,看到就是赚到
你可以在家做正式的兼职工作。在线兼职工作值得考虑,时间相对自由。在线兼职收入可能不如线下滴滴和外卖立竿见影,但仍然可以坚持收入。有些人比工作工资发展得更高。当然,天上不会有馅饼,不劳无获。那么有哪些正规的兼职可以在家…...
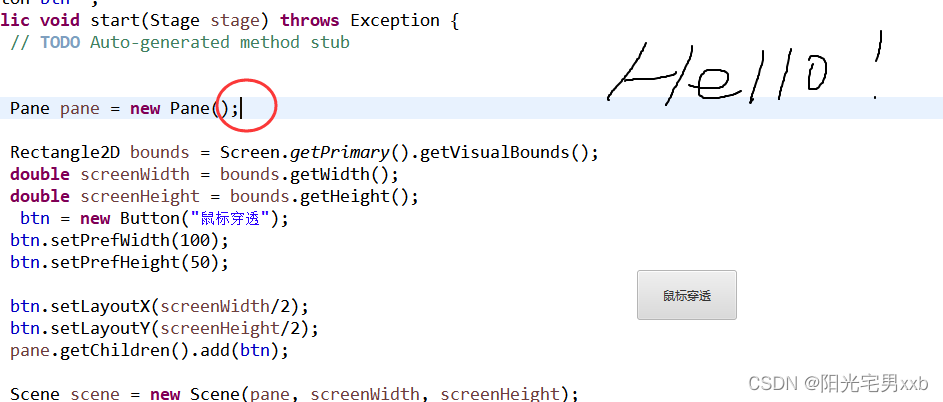
javaFx实现鼠标穿透画布,同时操作画布和桌面,背景透明,类似ppt批注
一、功能需要由来和大致效果 今天,我们要用javaFx来实现一个鼠标穿透画布的功能,该需求来自于在我们的javaFx桌面应用中,需要实现一个悬浮的桌面侧边工具栏,在工具栏中有画笔绘制,批注的功能,能够实现在任何…...

客户服务知识库的最佳实践7个步骤
每个公司的声誉都依赖于客户,如果客户因为想要购买你的产品找到你,但是了解到你的客户服务做的不好,可能也会放弃你的产品,就像市场营销依赖于潜在客户的关系一样,公司的服务部门也需要依赖于现有客户的关系࿰…...
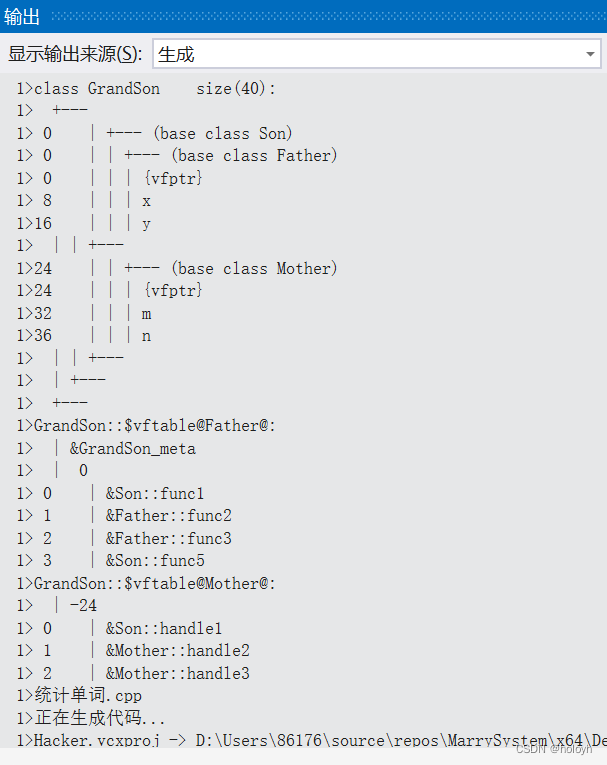
多重继承的虚函数表
同一个类,不同对象使用同一张虚函数表 不同类使用不同的虚函数表 子类自己添加的虚函数(非重写),在VS中是将此放在第一个继承类的虚函数表里. #include <iostream> using namespace std;class Father { public:virtual void func1() { cout << "Father::f…...

第11篇:Java开发工具使用和代码规范配置
目录 1、IntelliJ IDEA 简介 2. IntelliJ IDEA 下载 3. IntelliJ IDEA 安装和使用 3.1 安装到Windows下 3.2 快速编写 Hello World 程序...

Rust模式匹配
模式匹配 模式匹配是从函数式编程语言(例如:Haskell,Lisp)吸收而来的,用于为复杂的类型系统提供一个轻松的解构能力。rust使用match来提供模式匹配的功能。mathc类似于其它编程语言中的switch-case,但是远…...

GIT:【基础一】必要配置和命令
目录 一、Git安装 二、基础命令 1.git config -l:git配置详细信息 2.git config --system -l:本地git系统自动配置的信息 3.git config --global -l:本地git用户自动配置的信息 4.where git: windows查看git安装目录 5.git各配置…...

黑马程序员-Linux系统编程-01
课程链接 01-Linux命令基础习惯-Linux系统编程_哔哩哔哩_bilibili 课程重点笔记 01-linux命令基础习惯 终端 终端:一切输入、输出的总称,因此终端并不是一定指的是命令行,只要是能进行输入或者输出即可,但是在linux终端上‘’内…...
Python|每日一练|动态规划|图算法|散列表|数组|双指针|单选记录:不同路径|求两个给定正整数的最大公约数和最小公倍数|删除有序数组中的重复项
1、不同路径(数学,动态规划) 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”…...
Java常用框架(一)
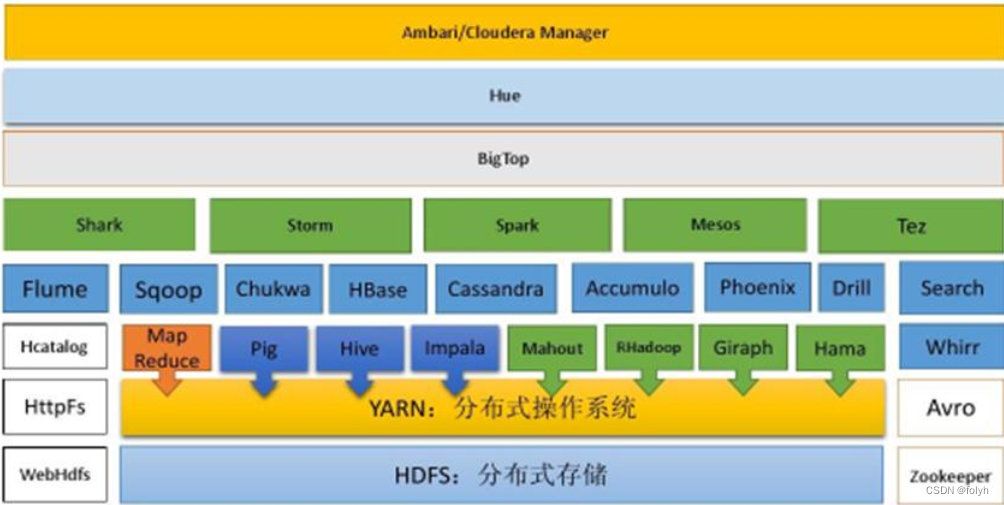
思维导图 常见知识点 一、SpringBoot 1.简单介绍一下Spring及其优缺点 1.1 概念 重量级企业开发框架EJB的替代品,通过依赖注入、面向切面编程,使用简单Java对象POJO为企业Java开发提供了相对简单的方法。 1.2 优缺点 1.2.1 优点 组件代码轻量级 …...
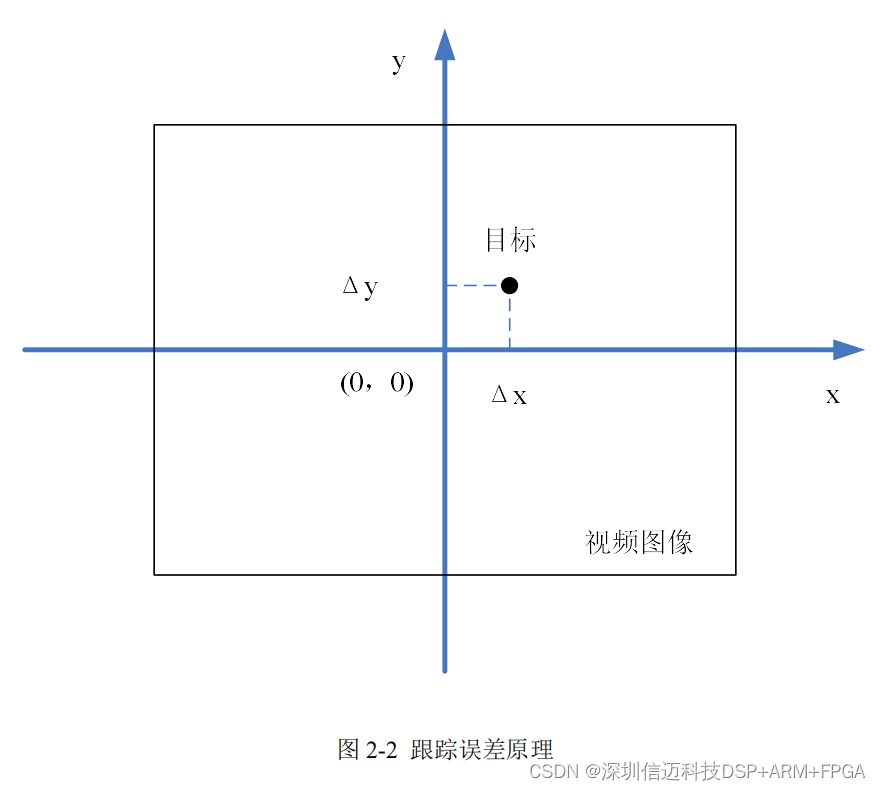
基于 DSP+FPGA 的高清图像跟踪系统研制
目标识别与跟踪技术是目前图像处理研究的重点方向,在军事和民用领域中 具有广泛的应用价值,如精确制导武器、导弹飞机预警等军事领域,如交通管理、 刑事侦查等民用领域。其中,如何在复杂的背景中,提取、识别与跟踪特定…...

apisix部署
使用k8s部署前打包镜像: FROM centos:7 ARG APISIX_VERSION2.11.0 LABEL apisix_version“${APISIX_VERSION}” RUN yum install -y https://repos.apiseven.com/packages/centos/apache-apisix-repo-1.0-1.noarch.rpm && yum install -y https://repos…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...
