递归算法应用(Python版)
文章目录
- 递归
- 递归定义
- 递归调用的实现
- 递归应用
- 数列求和
- 任意进制转换
- 汉诺塔
- 探索迷宫
- 找零兑换-递归
- 找零兑换-动态规划
- 递归可视化
- 简单螺旋图
- 分形树:自相似递归图像
- 谢尔宾斯基三角
- 分治策略
- 优化问题和贪心策略
递归
递归定义
递归是一种解决问题的方法,其精髓在于将问题分解为规模更小的相同问题,持续分解,直到问题规模小到可以用非常简单直接的方式来解决。
递归的问题分解方式非常独特,其算法方面的明显特征就是:在算法流程中调用自身。递归为我们提供了一种对复杂问题的优雅解决方案,精妙的递归算法常会出奇简单
递归三定律
- 递归算法必须有一个基本结束条件(最小规模问题的直接解决)
- 递归算法必须能改变状态向基本结束条件演进(减小问题规模)
- 递归算法必须调用自身(解决减小了规模的相同问题)
递归调用的实现
当一个函数被调用的时候,系统会把调用时的现场数据压入到系统调用栈
- 每次调用,压入栈的现场数据称为栈帧当函数返回时,要从调用栈的栈顶取得返回地址,恢复现场,弹出栈帧,按地址返回。

递归深度限制
在调试递归算法程序的时候经常会碰到这样的错误: RecursionError
- 递归的层数太多,系统调用栈容量有限
这时候要检查程序中是否忘记设置基本结束条件,导致无限递归
- 或者向基本结束条件演进太慢,导致递归层数太多,调用栈溢出
在Python内置的sys模块可以获取和调整最大递归深度
import sys
# 默认递归深度
print(sys.getrecursionlimit()) # 1000
# 修改递归深度为3000
sys.setrecursionlimit(3000)
print(sys.getrecursionlimit()) # 3000
递归应用
数列求和
问题:给定一个列表,返回所有数的和
- 列表中数的个数不定,需要一个循环和一个累加变量来迭代求和
- 假如没有循环语句?既不能用for,也不能用while对不确定长度的列表求和?
换个方式来表达数列求和:全括号表达式(1+(3+(5+(7+9))))
- 上面这个式子,最内层的括号(7+9) ,这是无需循环即可计算的,实际上整个求和的过程是这样:
-
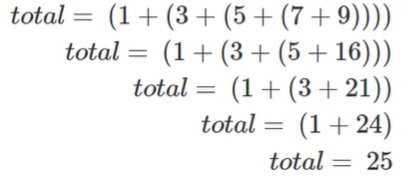
跟据上述过程中所包含的重复模式,可以把求和问题归纳成这样:
- 数列的和= “首个数” +“余下数列”的和
如果数列包含的数少到只有1个的话,它的和就是这个数了
- 这是规模小到可以做最简单的处理

def list_sum(num_list):if len(num_list) == 1: # 最小规模return num_list[0]else: # 减小规模return num_list[0] + list_sum(num_list[1:]) # 调用自身print(list_sum([1, 3, 5, 7, 9]))
# 25
- 问题分解为更小规模的相同问题,并表现为“调用自身”
- 对“最小规模”问题的解决:简单直接
递归函数执行过程
递归函数调用和返回过程的链条
- 先调用最小规模,然后一层一层往回
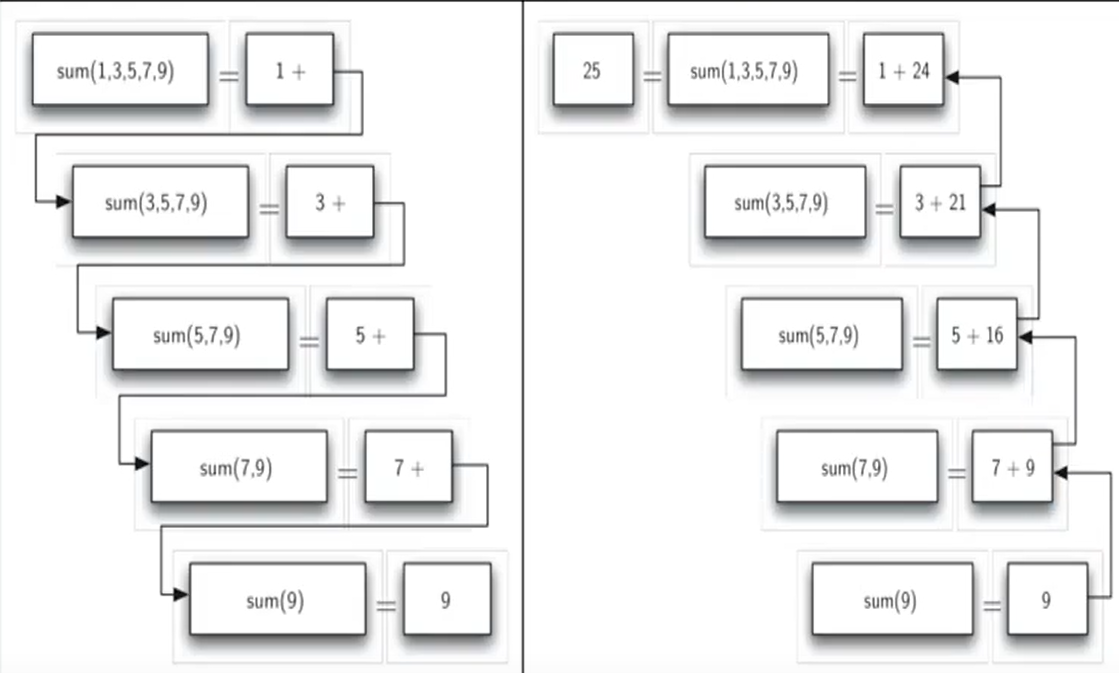
数列求和问题首先具备了基本结束条件:当列表长度为1的时候,直接输出所包含的唯一数
数列求和处理的数据对象是一个列表,而基本结束条件是长度为1的列表,那递归算法就要改变列表并向长度为1的状态演进
- 我们看到其具体做法是将列表长度减少1。
调用自身是递归算法中最难理解的部分,实际上我们理解为"问题分解成了规模更小的相同问题"就可以了
- 在数列求和算法中就是“更短数列的求和问题”
任意进制转换
整数转换任意进制
-
十进制有十个不同符号:convString"0123456789"
-
比十小的整数,转换成十进制,直接查表就可以了: convString[n]
-
把比十大的整数,拆成一系列比十小的整数,逐个查表
-
比如七百六十九,拆成七、六、九,查表得到769就可以了
在递归三定律里,我们找到了"基本结束条件",就是小于十的整数
- 拆解整数的过程就是向“基本结束条件”演进的过程
我们用整数除,和求余数两个计算来将整数一步步拆开
- 除以“进制基base" (// base)对“进制基”求余数(% base)
问题分解
-
余数总小于“进制基base”,是“基本结束条件”,可直接进行查表转换
-
整数商成为“更小规模”问题,通过递归调用自身解决

def to_str(n, base):convert_string = "0123456789ABCDEF"if n < base:return convert_string[n] # 最小规模else:# 将商作为新的被除数return to_str(n//base, base) + convert_string[n%base] # 减小规模,调用自身print(to_str(1453, 16)) # 5AD
汉诺塔
复杂递归问题
传说在一个印度教寺庙里,有3根柱子,其中一根套着64个由小到大的黄金盘片,僧侣们的任务就是要把这一叠黄金盘从一根柱子搬到另一根,但有两个规则:
-
一次只能搬1个盘子
-
大盘子不能叠在小盘子上
虽然这些黄金盘片跟世界末日有着神秘的联系,但我们却不必太担心,据计算,要搬完这64个盘片:
-
需要的移动次数为264-1 =18,446,744,073,709,551,615次
-
如果每秒钟搬动一次,则需要584,942,417,355(五千亿)年!
我们还是从递归三定律来分析河内塔问题
- 基本结束条件(最小规模问题),如何减小规模,调用自身
分解为递归形式
假设我们有5个盘子,穿在1#柱,需要拥到3#柱
-
如果能有办法把最上面的一摞4个盘子统统挪到2#柱,
-
把剩下的最大号盘子直接从1#柱挪到3#柱
-
再用同样的办法把2#柱上的那一摞4个盘子挪到3#柱,就完成了整个移动

递归思路
将盘片塔从开始柱,经由中间柱,移动到目标柱:
- 首先将上层N-1个盘片的盘片塔,从开始柱,经由目标柱,移动到中间柱;
- 然后将第N个(最大的)盘片,从开始柱,移动到目标柱;
- 最后将放置在中间柱的N-1个盘片的盘片塔,经由开始柱,移动到目标柱。
基本结束条件,也就是最小规模问题是:
- 1个盘片的移动问题
def move_tower(height, from_pole, with_pole, to_pole):if height >= 1:move_tower(height - 1, from_pole, to_pole, with_pole)move_disk(height, from_pole, to_pole)move_tower(height - 1, with_pole, from_pole, to_pole)def move_disk(disk, from_pole, to_pole):print(f"Moving disk[{disk}] from {from_pole} to {to_pole}")move_tower(3, "#1", "#2", "#3")
# Moving disk[1] from #1 to #3
# Moving disk[2] from #1 to #2
# Moving disk[1] from #3 to #2
# Moving disk[3] from #1 to #3
# Moving disk[1] from #2 to #1
# Moving disk[2] from #2 to #3
# Moving disk[1] from #1 to #3
探索迷宫
将海龟放在迷宫中间,如何能找到出口
首先,我们将整个迷宫的空间(矩形)分为行列整齐的方格,区分出墙壁和通道。
- 给每个方格具有行列位置,并赋予“墙壁”、通道”的属性
迷宫数据结构
考虑用矩阵方式来实现迷宫数据结构
- 采用“数据项为字符列表的列表”这种两级列表的方式来保存方格内容
- 采用不同字符来分别代表“墙壁+”、“通道”、“海龟投放点S"
- 从一个文本文件maze2.txt逐行读入迷宫数据
maze2.txt
++++++++++++++++++++++
+ + ++ ++ ++ ++++++++++
+ + ++ ++++ +++ ++
+ + + + ++ +++ +
+ ++ ++ + +
+++++ + + ++ + +
+++++ +++ + + ++ +
+ + + S+ + +
+++++ + + + + + +
++++++++++++++++++++++
读入数据文件成功后
- mazelist如下图示意
- mazelist[row] [col]==‘+’

算法思路
确定了迷宫数据结构之后,我们知道,对于海龟来说,其身处某个方格之中
-
它所能移动的方向,必须是向着通道的方向
-
如果某个方向是墙壁方格,就要换一个方向移动

这样,探索迷宫的递归算法思路如下:
- 将海龟从原位置向北移动一步,以新位置递归调用探索迷宫寻找出口;
- 如果上面的步骤找不到出口,那么将海龟从原位置向南移动一步,以新位置递归调用探索迷宫;
- 如果向南还找不到出口,那么将海龟从原位置向西移动一步,以新位置递归调用探索迷宫;
- 如果向西还找不到出口,那么将海龟从原位置向东移动一步,以新位置递归调用探索迷宫;如果上面四个方向都找不到出口,那么这个迷宫没有出口!
特殊细节:
- 如果我们向某个方向(如北)移动了海龟,那么如果新位置的北正好是一堵墙壁,那么在新位置上的递归调用就会让海龟向南尝试
- 可是新位置的南边一格,正好就是递归调用之前的原位置,这样就陷入了无限递归的死循环之中
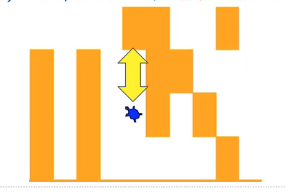
所以需要有个机制记录海龟所走过的路径(不走重复的路)
- 沿途洒“面包屑”,一旦前进方向发现“面包屑”,就不能再踩上去,而必须换下一个方向尝试对于递归调用来说,就是某方向的方格上发现“面包屑”,就立即从递归调用返回上一级。

递归调用的“基本结束条件”归纳如下:
- 海龟碰到“墙壁”方格,递归调用结束,返回失败;
- 海龟碰到“面包屑”方格,表示此方格已访问过,递归调用结束,返回失败;
- 海龟碰到“出口”方格,即“位于边缘的通道”方格,递归调用结束,返回成功!
- 海龟在四个方向上探索都失败,递归调用结束,返回失败
辅助动画过程
为了让海龟在迷宫图里跑起来,我们给迷宫数据结构Maze Class添加一些成员和方法
- t:一个作图的海龟,设置其shape为海龟的样子(缺省是一个箭头)
- drawMaze():绘制出迷宫的图形,墙壁用实心方格绘制
- updatePosition(row, col, val):更新海龟的位置,并做标注
- isExit(row, col):判断是否“出口”
import turtlePART_OF_PATH = 'O'
TRIED = '.'
OBSTACLE = '+'
DEAD_END = '-'def drawMaze(self):self.t.speed(10)for y in range(self.rowsInMaze):for x in range(self.columnsInMaze):if self.mazelist[y][x] == OBSTACLE:self.drawCenteredBox(x+self.xTranslate,-y+self.yTranslate,'orange')self.t.color('black')self.t.fillcolor('blue')def drawCenteredBox(self,x,y,color):self.t.up()self.t.goto(x-.5,y-.5)self.t.color(color)self.t.fillcolor(color)self.t.setheading(90)self.t.down()self.t.begin_fill()for i in range(4):self.t.forward(1)self.t.right(90)self.t.end_fill()def moveTurtle(self,x,y):self.t.up()self.t.setheading(self.t.towards(x+self.xTranslate,-y+self.yTranslate))self.t.goto(x+self.xTranslate,-y+self.yTranslate)def dropBreadcrumb(self,color):self.t.dot(10,color)def updatePosition(self,row,col,val=None):if val:self.mazelist[row][col] = valself.moveTurtle(col,row)if val == PART_OF_PATH:color = 'green'elif val == OBSTACLE:color = 'red'elif val == TRIED:color = 'black'elif val == DEAD_END:color = 'red'else:color = Noneif color:self.dropBreadcrumb(color)def isExit(self,row,col):return (row == 0 orrow == self.rowsInMaze-1 orcol == 0 orcol == self.columnsInMaze-1 )def __getitem__(self,idx):return self.mazelist[idx]
主函数
def searchFrom(maze, startRow, startColumn):# try each of four directions from this point until we find a way out.# base Case return values:# 1.碰到墙壁,返回失败maze.updatePosition(startRow, startColumn)if maze[startRow][startColumn] == OBSTACLE :return False# 2. 碰到面包屑,或死胡同,返回失败if maze[startRow][startColumn] == TRIED or maze[startRow][startColumn] == DEAD_END:return False# 3. 碰到出口,返回成功if maze.isExit(startRow,startColumn):maze.updatePosition(startRow, startColumn, PART_OF_PATH)return True# 4. 撒一下面包屑,继续探索maze.updatePosition(startRow, startColumn, TRIED)# 向北南西东4个方向依次探索,or操作符具有短路效应(减小规模)found = searchFrom(maze, startRow-1, startColumn) or \searchFrom(maze, startRow+1, startColumn) or \searchFrom(maze, startRow, startColumn-1) or \searchFrom(maze, startRow, startColumn+1)# 如果探索成功,标记当前点,失败则标记为死胡同if found:maze.updatePosition(startRow, startColumn, PART_OF_PATH)else:maze.updatePosition(startRow, startColumn, DEAD_END)return found
测试运行
myMaze = Maze('maze2.txt')
myMaze.drawMaze()
myMaze.updatePosition(myMaze.startRow,myMaze.startCol)searchFrom(myMaze, myMaze.startRow, myMaze.startCol)

找零兑换-递归
我们来找一种肯定能找到最优解的方法
- 贪心策略是否有效依赖于具体的硬币体系
首先是确定基本结束条件,兑换硬币这个问题最简单直接的情况就是,需要兑换的找零,其面值正好等于某种硬币
- 如找零25分,答案就是1个硬币!
其次是减小问题的规模,我们要对每种硬币尝试1次,例如美元硬币体系:
- 找零减去1分(penny)后,求兑换硬币最少数量(递归调用自身);
- 找零减去5分(nikel)后,求兑换硬币最少数量
- 找零减去10分(dime)后,求兑换硬币最少数量
- 找零减去25分(quarter)后,求兑换硬币最少数量上述4项中选择最小的一个。

def rec_mc(coin_value_list, change):min_coins = changeif change in coin_value_list:return 1 # 最小规模,直接返回else:for i in [c for c in coin_value_list if c <= change]:num_coins = 1 + rec_mc(coin_value_list, change - i) # 调用自身,减小规模,每次减去一种硬币面值,挑选最小数量if num_coins < min_coins:min_coins = num_coinsreturn min_coinsprint(rec_mc([1, 5, 10, 25], 45)) # 3
- 虽然能解决问题,但极其低效,如果将45改成更大的数需要运行很长时间
- 原因:重复计算太多
递归算法改进
对这个递归解法进行改进的关键就在于消除重复计算
- 我们可以用一个表将计算过的中间结果保存起来,在计算之前查表看看是否已经计算过
这个算法的中间结果就是部分找零的最优解,在递归调用过程中已经得到的最优解被记录下来
- 在递归调用之前,先查找表中是否已有部分找零的最优解
- 如果有,直接返回最优解而不进行递归调用如果没有,才进行递归调用
优化后的代码
def rec_mc(coin_value_list, change, known_results): # 硬币面值列表,找零,最优解min_coins = changeif change in coin_value_list: # 递归结束基本结束条件known_results[change] = 1 # 记录最优解return 1 # 最小规模,直接返回elif known_results[change] > 0:return known_results[change] # 查表成功,直接用最优解else:for i in [c for c in coin_value_list if c <= change]:num_coins = 1 + rec_mc(coin_value_list, change - i, known_results) # 调用自身,减小规模,每次减去一种硬币面值,挑选最小数量if num_coins < min_coins:min_coins = num_coinsknown_results[change] = min_coinsreturn min_coinsprint(rec_mc([1, 5, 10, 25], 63, [0] * 64)) # 6
- 改进后的算法,极大减少了递归调用的次数
找零兑换-动态规划
动态规划解法
中间结果记录可以很好解决找零兑换问题
实际上,这种方法还不能称为动态规划,而是叫做"memoization (记忆化/函数值缓存)"的技术提高了递归解法的性能
动态规划算法采用了一种更有条理的方式来得到问题的解
找零兑换的动态规划算法从最简单的“1分钱找零”的最优解开始,逐步递加上去,直到我们需要的找零钱数
在找零递加的过程中,设法保持每一分钱的递加都是最优解,一直加到求解找零钱数,自然得到最优解
递加的过程能保持最优解的关键是,其依赖于更少钱数最优解的简单计算,而更少钱数的最优解已经得到了。、
问题的最优解包含了更小规模子问题的最优解,这是一个最优化问题能够用动态规划策略解决的必要条件。

递归可视化
递归可视化:图示
python turtle库
turtle — 海龟绘图 — Python 3.8.17 文档
Python的海龟作图系统turtle module
-
Python内置,随时可用,以LOGO语言的创意为基础
-
其意象为模拟海龟在沙滩上爬行而留下的足迹
-
爬行: forward(n); backward(n)
-
转向: left(a); right(a)
-
抬笔放笔: penup(); pendown()
-
笔属性: pensize(s); pencolor©
简单螺旋图
import turtle
t = turtle.Turtle()
def draw_spiral(t, line_len):if line_len > 0: # 最小规模0直接退出t.forward(line_len)t.right(90)draw_spiral(t, line_len - 5) # 减小规模边长减5,调用自身

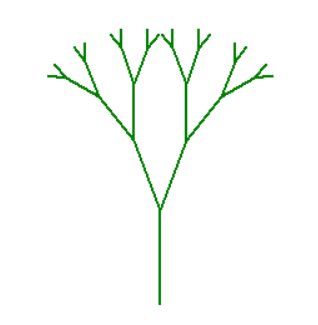
分形树:自相似递归图像
分形Fractal ,是1975年由Mandelbrot开创的新学科
- “一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”,即具有自相似的性质。
我们可以把树分解为三个部分:树干、左边的小树右边的小树
- 分解后,正好符合递归的定义:对自身的调用

import turtledef tree(branch_len): # 树干长度if branch_len > 5: # 树干最短限制,递归结束条件t.forward(branch_len) # 画树干t.right(20) # 右倾斜20度tree(branch_len - 15) # 递归调用,画右边小树,树干减15t.left(40) # 向左40度,即左倾斜20度tree(branch_len - 15) # 递归调用,画左边小树,树干减15t.right(20) # 向右回20度,即回正t.backward(branch_len) # 海龟回到原位置
# 由于递归特性,每次退回原位置先退最短的然后逐渐增加,类似栈后进先出,branch_len是最后的值往前
t = turtle.Turtle()
t.left(90)
t.penup()
t.backward(100)
t.pendown()
t.pencolor("green")
t.pensize(2)
tree(75) # 画树干长度75的二叉树
t.hideturtle() # 隐藏光标
turtle.exitonclick()
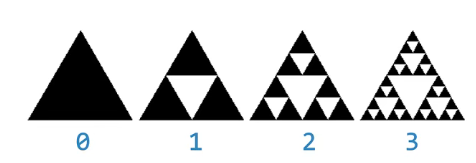
谢尔宾斯基三角
分形构造,平面称谢尔宾斯基三角形,立体称谢尔宾斯基金字塔
-
在一个等边三角形中,不断地被挖去最大的倒等边三角形
-
实际上,真正的谢尔宾斯基三角形是完全不可见的,其面积为0,但周长无穷,是介于一维和二维之间的分数维(约1.585维)构造。
作图思路
根据自相似特性,谢尔宾斯基三角形是由3个尺寸减半的谢尔宾斯基三角形按照品字形拼叠而成
- 由于我们无法真正做出谢尔宾斯基三角形(degree->0),只能做degree有限的近似图形。
在degree有限的情况下,degree=n的三角形,是由3个degree=n-1的三角形按照品字形拼叠而成
- 同时,这3个degree=n-1的三角形边长均为degree=n的三角形的一半(规模减小)。当degree=0,则就是一个等边三角形,这是递归基本结束条件
绘制等边三角形
import turtle
# 绘制等边三角形
def draw_triangle(points, color):t.fillcolor(color)t.penup()t.goto(points["top"])t.pendown()t.begin_fill()t.goto(points["left"])t.goto(points["right"])t.goto(points["top"])t.end_fill()
三角形顶点坐标
def get_mid(p1, p2): # 取两个点中点return ((p1[0] + p2[0]) / 2, (p1[1] + p2[1]) / 2)
谢尔宾斯基三角
def sierpinski(degree, points):color_map = ["blue", "red", "green", "white", "yellow", "orange"]draw_triangle(points, color_map[degree])# 画等边三角形if degree > 0: # 最小规模,0直接退出# 减小规模,getMid边长减半# 调用自身安装从左到上到右的顺序sierpinski(degree - 1,# 调用自身,左方顶点{"left":points["left"],"top":get_mid(points["left"], points["top"]),"right":get_mid(points["left"], points["right"])})sierpinski(degree - 1,# 调用自身,上方顶点{"left":get_mid(points["left"], points["top"]),"top":points["top"],"right":get_mid(points["top"], points["right"])})sierpinski(degree - 1,# 调用自身,右方顶点{"left":get_mid(points["left"], points["right"]),"top":get_mid(points["top"], points["right"]),"right":points["right"]})
测试degree = 5 的三角形
# 最开始外轮廓三个顶点
points = {"left":(-200, -100),"top":(0, 200),"right":(200, -100)}
t = turtle.Turtle()
sierpinski(5, points) # 画阶数为5的三角形
turtle.exitonclick()

图示degree = 3绘制过程

分治策略
解决问题典型策略:分而治之
- 将问题分为若干更小规模的部分
- 通过解决每一个小规模部分问题,并将结果汇总得到原问题的解

递归算法与分治策略
递归三定律:
- 基本结束条件,解决最小规模问题缩小规模,向基本结束条件演进调用自身来解决已缩小规模的相同问题
体现了分治策略问题
- 解决依赖于若干缩小了规模的问题汇总得到原问题的解
应用:
- 排序、查找、遍历、求值等等
优化问题和贪心策略
计算机科学中许多算法都是为了找到某些问题的最优解
- 例如,两个点之间的最短路径;能最好匹配一系列点的直线;或者满足一定条件的最小集合
找零兑换问题
一个经典案例是兑换最少个数的硬币问题
-
假设你为一家自动售货机厂家编程序,自动售货机要每次找给顾客最少数量硬币;
-
假设某次顾客投进$1纸币,买了£37的东西,要找g63,那么最少数量就是: 2个quarter (g25)、1个dime (g10)和3个p
-
来解决这些问题,例如最直观的“贪心策略”一般我们这么做:从最大面值的硬币开始,用尽量多的数量有余额的,再到下一最大面值的硬币,还用尽量多的数量,一直到penny (g1)为止

贪心策略
- 因为我们每次都试图解决问题的尽量大的一部对应到兑换硬币问题,就是每次以最多数量的大面值硬币来迅速减少找零面值
相关文章:

递归算法应用(Python版)
文章目录 递归递归定义递归调用的实现递归应用数列求和任意进制转换汉诺塔探索迷宫找零兑换-递归找零兑换-动态规划 递归可视化简单螺旋图分形树:自相似递归图像谢尔宾斯基三角 分治策略优化问题和贪心策略 递归 递归定义 递归是一种解决问题的方法,其精…...
有什么react进阶的项目推荐的?
前言 整理了一些react相关的项目,可以选择自己需要的练习,希望对你有帮助~ 1.ant-design Star:87.1k 阿里开源的react项目,作为一个UI库,省去重复造轮子的时间 仓库地址:https://github.com/ant-design/…...
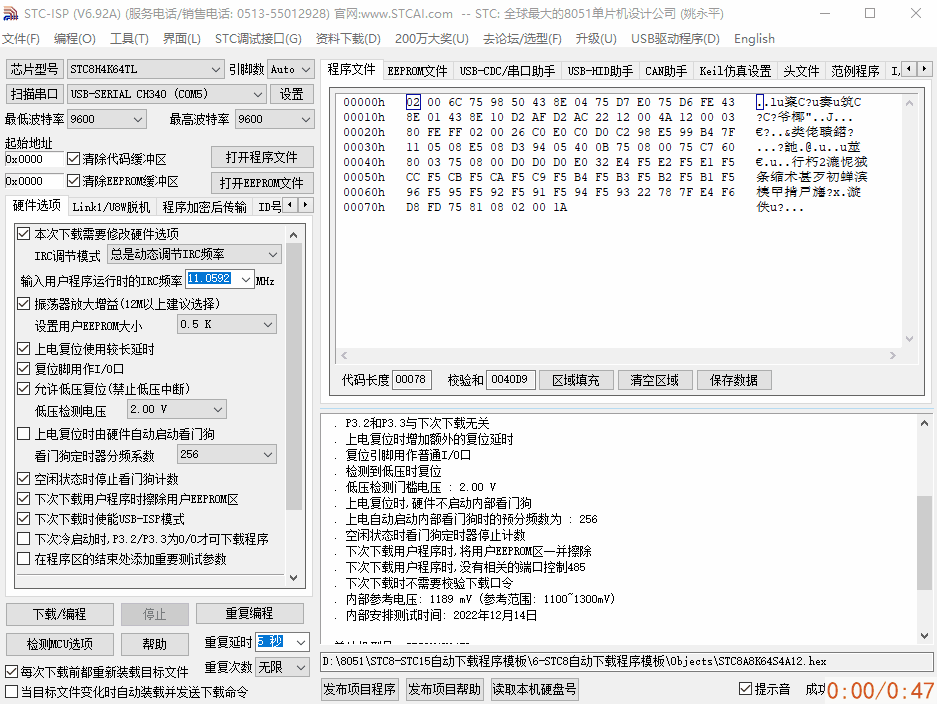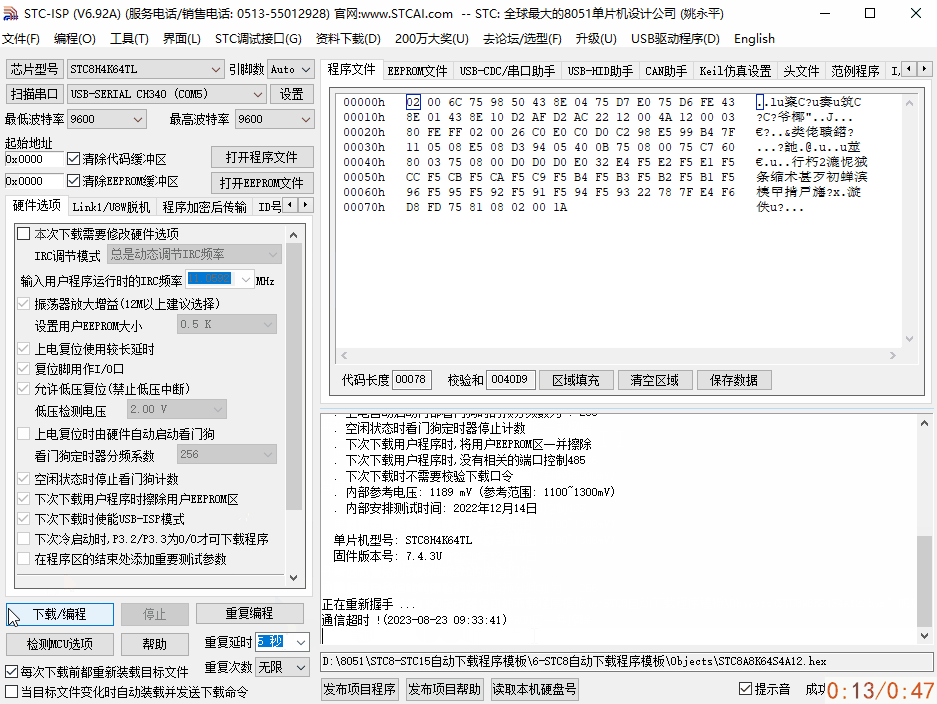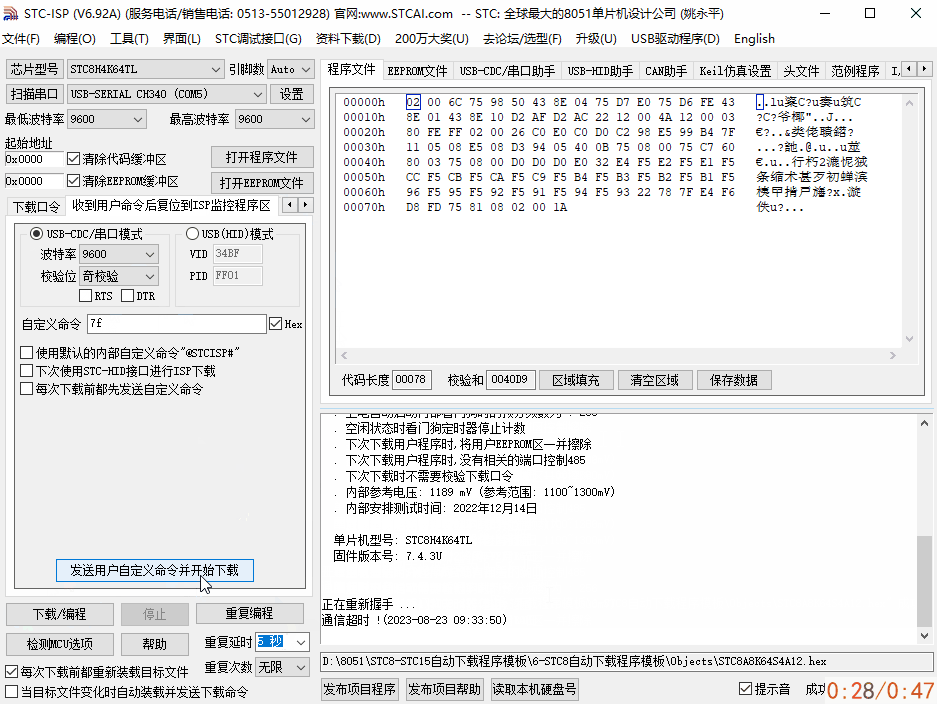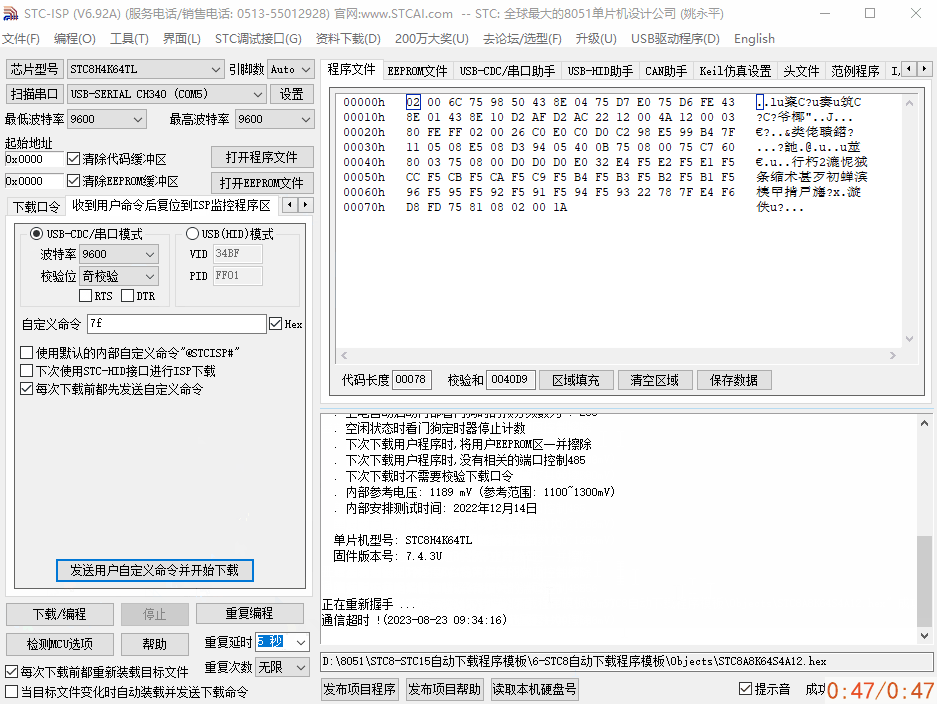
基于串口透传模块,单片机无线串口空中下载测试
基于串口透传模块,单片机无线串口空中下载测试 ✨无线串口下载,其本质还是串口下载方式,只不过省去了单片机和ISP上位机工具之间的物理有线连接,中间的数据通过无线串口透传模块进行数据中转,传递到单片机串口上。串口…...

研磨设计模式day11代理模式
目录 场景 代码实现 编辑 解析 定义 代理模式调用示意图 代理模式的特点 本质 编辑何时选用 场景 我有一个订单类,包含订单数、用户名和商品名,有一个订单接口包含了对订单类的getter和setter 现在有一个需求,a创建的订单只…...

vue2 路由进阶,VueCli 自定义创建项目
一、声明式导航-导航链接 1.需求 实现导航高亮效果 如果使用a标签进行跳转的话,需要给当前跳转的导航加样式,同时要移除上一个a标签的样式,太麻烦!!! 2.解决方案 vue-router 提供了一个全局组件 router…...
《C语言编程环境搭建》工欲善其事 必先利其器
C语言编译器 GCC 系列 GNU编译器套装(英语:GNU Compiler Collection,缩写为GCC),指一套编程语言编译器,常被认为是跨平台编译器的事实标准。原名是:GNU C语言编译器(GNU C Compiler)。 MinGW 又称mingw32 ,…...

蓝蓝设计ui设计公司作品案例-中节能现金流抗压测试软件交互及界面设计
中国节能是以节能环保为主业的中央企业。中国节能以生态文明建设为己任,长期致力于让天更蓝、山更绿、水更清,让生活更美好。经过多年发展,中国节能已构建起以节能、环保、清洁能源、健康和节能环保综合服务为主业的41产业格局,成…...

汽车制造业外发文件时 如何阻断泄密风险?
汽车制造业是我国国民经济发展的支柱产业之一,具有产业链长、关联度高、就业面广、消费拉动大等特性。汽车制造行业景气度与宏观经济、居民收入水平和固定资产投资密切相关。 汽车制造业产业链长,关联度高,汽车制造上游行业主要为钢铁、化工…...

怎么对App进行功能测试
测试人员常被看作是bug的寻找者,但你曾想过他们实际是如何开展测试的吗?你是否好奇他们究竟都做些什么,以及他们如何在一个典型的技术项目中体现价值?本文将带你经历测试人员的思维过程,探讨他们测试app时的各种考虑. …...
)
数字流的秩、单词频率(哈希实现)
题目1:数字流的秩 假设你正在读取一串整数。每隔一段时间,你希望能找出数字 x 的秩(小于或等于 x 的值的个数)。请实现数据结构和算法来支持这些操作,也就是说: 实现 track(int x) 方法,每读入一个数字都会调用该方法…...
【洛谷】P2678 跳石头
原题链接:https://www.luogu.com.cn/problem/P2678 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 二分答案。(使用二分需要满足两个条件。一个是有界,一个是单调。 这题的题面:使得选手们在比赛过程中…...
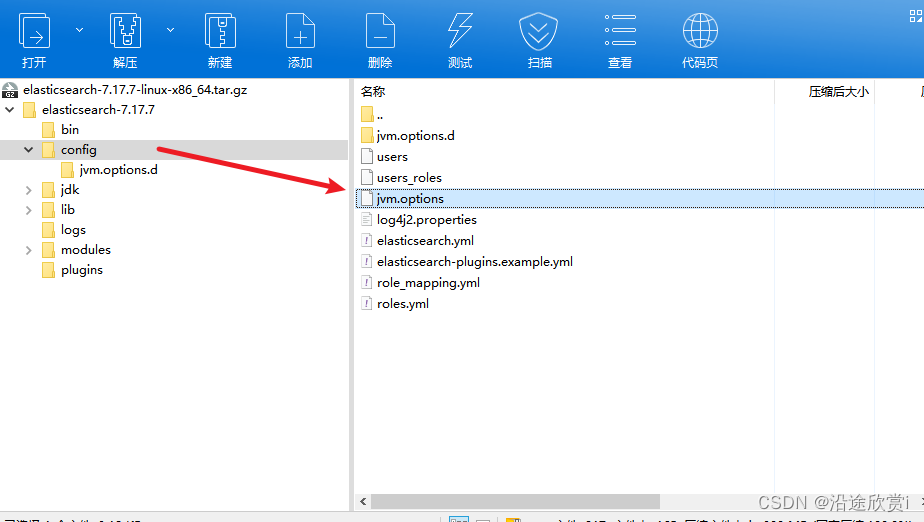
Elasticsearch配置优化
以下的优化基础是安装的 Elasticsearch 版本为 7.17.7,同时jdk版本为 1.8.321 1、jvm参数优化 这里说的jvm参数调优,是指elasticsearch安装目录下的jvm.options配置,如下图所示: 这里调整的内容主要是调整垃圾回收的收集器&#…...

Springboot整合minio组件-分布式文件存储
一、快速开始 Minlo说明: Minio是Apcche旗下的一款开源的轻量级文件服务器,基于对象存储,协议是基于Apache License v2.0,开源可用于商务。Minio主要用来存储非结构化的数据,类似文件,图片,照…...

多态/虚函数/虚函数表
OVERVIEW 多态/虚函数/虚函数表1.虚函数引入后类发生的变化?2.虚函数表的生成时机和生成原因?3.虚函数表指针赋值的时机?4.类对象在内存中的布局?5.虚函数的工作原理和多态性的体现?6.其他问题 多态/虚函数/虚函数表 n…...
QT中按钮的基类QAbstractButton
QT中按钮的基类QAbstractButton 关于控件类的学习方法继承关系信号槽函数标题和图标按钮的 Check 属性 关于控件类的学习方法 控件类很多,API更多,但是不需要记忆知道控件对应的类名,通过帮助文档随用随查优先看帮助文档中控件对应的信号和槽…...
)
并查集(种类并查集,带权并查集)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题目描述 动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形。A吃B,B吃C,C吃A。 现有N个动物,以1-N编号。每个动物都…...

飞天使-k8s基础组件分析-控制器
文章目录 控制器含义解释pod的标签与注释ReplicaControllerReplicaSetDeploymentsDaemonSetJobCronjob参考文档 控制器含义解释 空调遥控器知道吧ReplicationController: ReplicationController确保在任何时候都运行指定数量的pod副本。换句话说,一个ReplicationCo…...
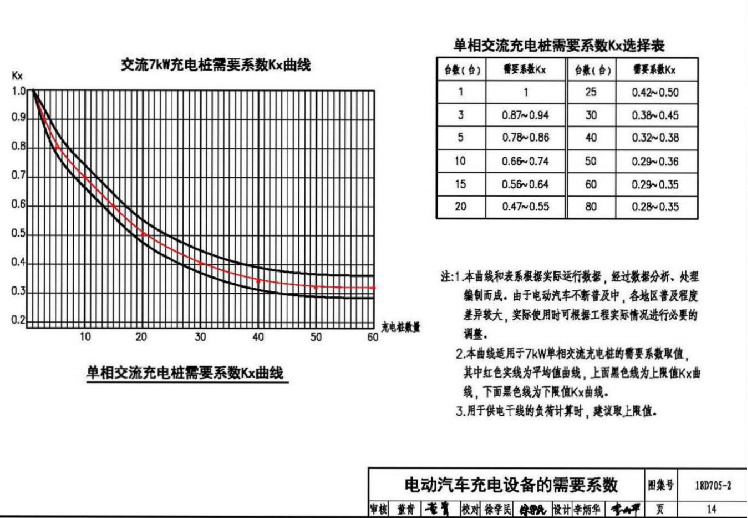
有序充电运营管理平台是基于物联网和大数据技术的充电设施管理系统-安科瑞黄安南
随着我国能源战略发展以及低碳行动的实施,电动汽车已逐步广泛应用,而电动汽车的应用非常符合当今社会对环保意识的要求,以及有效节省化石燃料的消耗。 由于其没有污染排放的优点以及政府部门的关注,电动汽车将成为以后出行的重要…...

LeetCode-227-基本计算器Ⅱ
题目描述: 给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。 整数除法仅保留整数部分。 你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。 注意:不允许使用任何将字符串作为数学表达式计…...

dart 学习列表 List
List 列表 在 Dart 编程语言中,List 是一种有序的集合数据类型,用于存储一系列项目。它允许您在单个变量中存储多个项目,并提供了许多操作来管理列表中的数据。以下是关于 Dart 中的 List 的一些重要信息: 创建 List: …...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)
漏洞概述 漏洞名称:Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号:CVE-2023-25194 CVSS评分:8.8 影响版本:Apache Kafka 2.3.0 - 3.3.2 修复版本:≥ 3.4.0 漏洞类型:反序列化导致的远程代…...
