什么是需求可追溯性,为什么它对产品团队很重要?
随着产品变得越来越复杂,需求在开发过程中将在各个部门和利益相关方之间不断传递。可追溯性能帮助产品团队解决他们在需求管理过程中面临的一大挑战。
目前产品开发需要做出的决策比以往任何时候都多,每一种决策都需要充分考虑对具体需求和整体产品的影响后再做出。所以能够清晰地了解正在进行的工作活动并将其关联起来非常重要。
这就需要依靠需求可追溯性。下面我们来探讨需求可追溯性的定义、目的、重要性、好处和面临的挑战。
常见的挑战
在实施需求可追溯性的过程中,项目团队可能会遇到各种挑战,但许多模板和工具可以帮助我们简化这个过程。接下来,将为大家提供一些策略和建议以应对一些常见的挑战。
1.不同的组织观点
不同人对追溯的理解和做法各有不同。管理层可能仅从规则规定层面考虑,将其视为必须做的事。他们可能不像项目或系统工程师那样,理解追溯的额外好处。我们可以通过教育提高管理层的认识,让他们知道实现端到端追溯可以达到什么目的。
2.组织范围的采用
一个组织可能因为各种原因延迟采用追溯。培训就是一个原因,不是所有人都理解追溯的重要性,也不知道如何正确执行。一些人可能担心追溯数据会被用来追责。我们需要培训,并创造将追溯视为固有过程的文化。制定清晰的追溯政策,并对所有员工进行培训。选择直观易用的追溯工具,使其适应我们的流程。
3.实施的成本
让整个组织执行追溯需要投入,会增加政策、培训、数据维护的时间,可能让人感觉效率降低。采用追溯工具也需要投资。要克服这点,我们需要改变思维方式。我们应考虑不追溯的成本,比如低效的工作、冗长的开发周期、返工和缺陷,这些都是非常昂贵的。虽然执行追溯和使用工具需要成本,但可以节省的成本远超过短期投入。
4.管理变更
在开发复杂产品时,变更不可避免。团队成员必须知道相关的系统需求、下游需求和验证测试都会受到影响。手工处理非常麻烦,风险也类似于不做任何变更管理,容易遗漏信息。我们可以采用自动化追溯工具,实现需求变更的实时追溯。
5.不当的管理工具
一些团队仍在用Word、Excel文档和邮件进行追溯,这对简单产品可能还行,但对复杂产品就面临种种挑战。文档无法满足变更追溯的需求。我们可以采用灵活的追溯工具(比如PingCode等),在团队和工具间建立追溯关系,获得更多益处。
6.不充分的合规框架
受监管行业需要管理需求,证明符合标准。审核需要以特定方式提交材料,必须提供完备的追溯证据。如果在开发过程没有全面追溯,审核会非常耗时。即使在文档中保留了追溯信息,也需要编译成可接受的格式。与此同时,将追溯作为内在流程的竞争对手将更快进入市场。我们可以选择与行业标准一致、具备导出功能的追溯工具,以简化合规审核过程。
简化流程的模版和工具
有许多工具可以简化端到端可追溯性流程,最好根据自己需求来选择适合的工具。
如果团队所开发的是相对简单的产品,且没有功能安全或合规要求,那么使用需求可追溯性矩阵(RTM)就足够了。
但是如果我们正在开发包含软件和硬件组件的复杂产品,并且需要安全证明或合规证明,那么我们可能需要一个能够提供双向可追溯性的需求管理工具。
相关文章:

什么是需求可追溯性,为什么它对产品团队很重要?
随着产品变得越来越复杂,需求在开发过程中将在各个部门和利益相关方之间不断传递。可追溯性能帮助产品团队解决他们在需求管理过程中面临的一大挑战。 目前产品开发需要做出的决策比以往任何时候都多,每一种决策都需要充分考虑对具体需求和整体产品的影…...
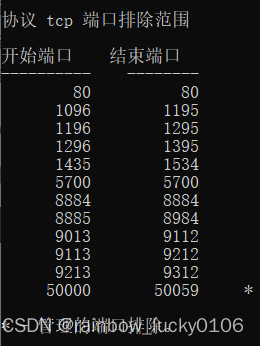
Window基础命令
文章目录 查看哪些端口被禁用TCP协议删除开机启动项方案1方案2 查看哪些端口被禁用TCP协议 netsh interface ipv4 show excludedportrange protocoltcp删除开机启动项 方案1 列出所有启动项 bcdedit /enum仔细看你要删除的是哪一项(看description)&a…...

Java List的扩容机制原理及应用
Java List的扩容机制原理及应用 引言 在Java中,List是一种非常常用的数据结构,用于存储有序的元素集合。List的底层实现有多种,如ArrayList、LinkedList等。在使用List时,我们经常会遇到一个问题:当元素数量超过了Li…...

Cesium 显示经纬高
文章目录 需求分析 需求 页面展示经、纬度和高 分析 html <div id"latlng_show" style"width:340px;height:30px;position:absolute;bottom:40px;right:200px;z-index:1;font-size:15px;"><div style"width:100px;height:30px;float:left;…...

专访 Hyper Oracle:可编程的 zkOracle 打造未来世界的超算
许多 Web3 应用在实现的过程中,常常会遇到基础设施方面的限制,包括去中心化自动化、预言机、链上信息搜索等问题。绝大部分区块链的中间件网络都是依赖于节点质押来保证节点执行的诚实性,这样的模式会产生诸多衍生问题,例如安全性…...

ThreadLocal存放当前用户
用户信息必须由后端获取,不能通过前端传入的id是不可信的,,可能会出现越权的问题,,,怎么通过后端获取当前登录用户,,, 就需要将User 和 当前线程绑定在一起,&…...

es入门实战
创建索引 PUT /hotel/ { “mappings”:{ “properties”:{ “title”:{ “type”:“text” }, “city”:{ “type”:“keyword” }, “price”:{ “type”:“double” } } } } 给索引写入数据 POST /hotel/_doc/001 { “title”:“好再来大酒店”, “city”:“东京”, “pri…...

c++系列之指针
今天不是做题系列,是知识系列啦。 说到指针,我们初学这一定会气的牙痒痒把,笔者也是,这么我好久而不得呀,今天来让我们聊聊指针。 其一 首先,我们明确的知道,假如我们开一个变量,…...

网络安全:挑战与防护策略
一、引言 随着科技的快速发展,互联网已经成为我们生活和工作的重要组成部分。然而,随着网络技术的不断升级,网络安全问题也日益凸显。网络攻击、数据泄露、身份盗用等问题,不仅威胁到个人隐私,也对企业和国家的安全构…...

AI 插件:未来的浏览器、前端与交互
想象一下,你在浏览器中粘贴一个 URL,这个 URL 不仅仅是一个网址,而是一个功能强大、能执行多种任务的 AI 插件。这听起来像是未来的事情,但实际上,这种变革已经悄悄进行中。 1. 插件的魅力与局限性 当我第一次接触到…...

R包开发-2.1:在RStudio中使用Rcpp制作R-Package(更新于2023.8.23)
目录 0-前言 1-在RStudio中创建R包项目 2-创建R包 2.1通过R函数创建新包 2.2在RStudio通过菜单来创建一个新包 2.3关于R包创建的说明 3-添加R自定义函数 4-添加C函数 0-前言 目标:在RStudio中创建一个R包,这个R包中包含C函数,接口是Rc…...

土豆叶病害识别(图像连续识别和视频识别)
效果视频:土豆叶病害识别(Python代码,pyTorch框架,视频识别)_哔哩哔哩_bilibili 代码运行要求:Torch库>1.13.1,其它库无版本要求 1..土豆叶数据集主要包好三种类别(Early_Blight…...
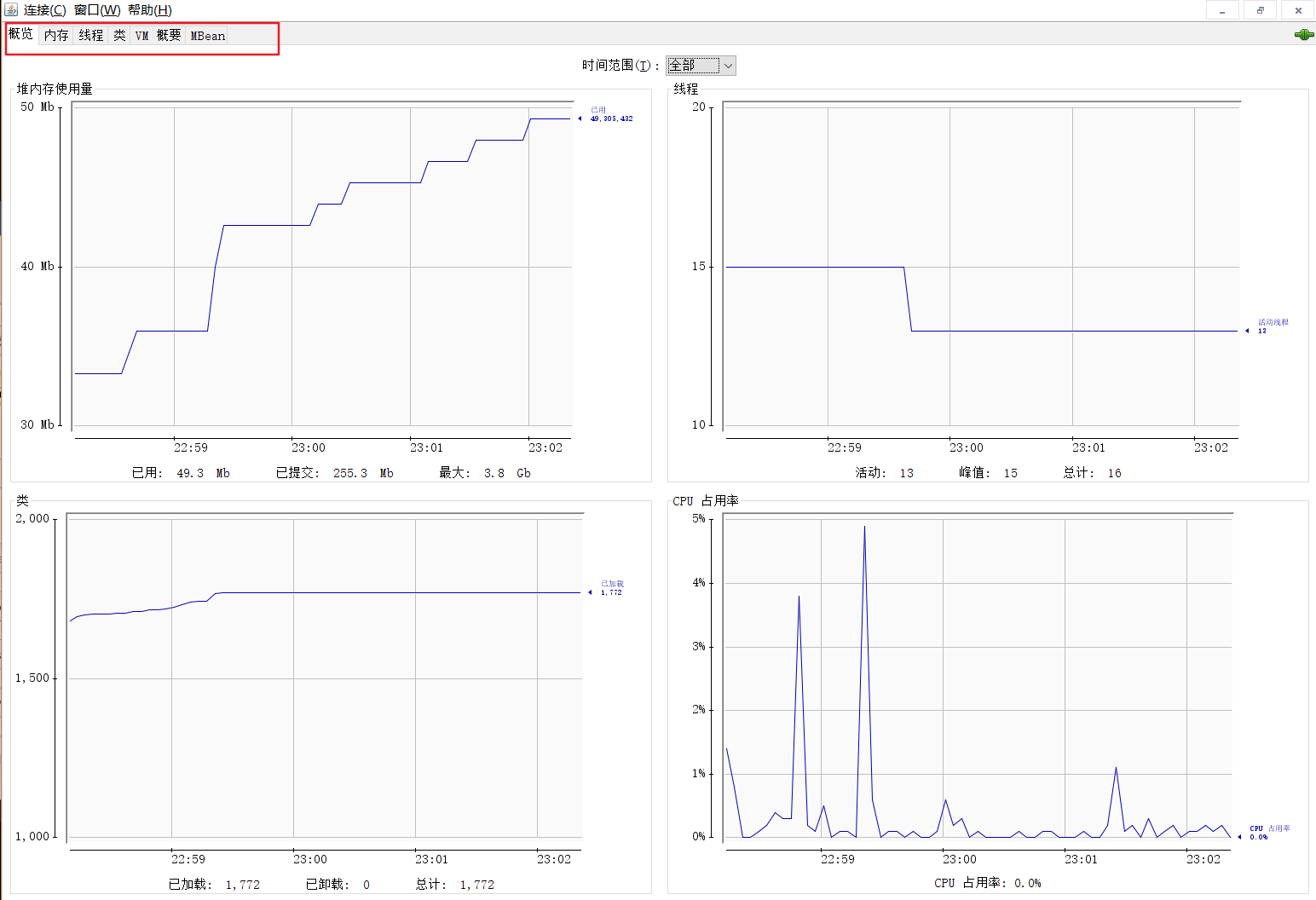
三、JVM监控及诊断工具-GUI篇
目录 一、工具概述二、jconsole(了解即可)1、基本概述2、启动3、三种连接方式4、作用 三、Visual VM 一、工具概述 二、jconsole(了解即可) 1、基本概述 从Java5开始,在JDK中自带的Java监控和管理控制台用于对JVM中内…...

3211064 - 错误消息 AA634 出现在 T-cd AW01N 或 T-cd AFAR 中
症状 通过 T-cd AW01N 打开资产或在 T-cd AFAR 中重新计算资产值时,出现以下错误消息: AA634 在范围 01 中普通折旧的更正大于累计折旧 环境 SAP R/3SAP R/3 EnterpriseSAP ERP SAP ERP 中心组件SAP ERP 的 SAP 增强包SAP ERP(SAP HANA 版…...

k3s or RKE2 helm安装报错dial tcp 127.0.0.1:8080: connect: connection refused
1.报错: Error: INSTALLATION FAILED: Kubernetes cluster unreachable: Get "http://127.0.0.1:8080/version": dial tcp 127.0.0.1:8080: connect: connection refused 2.问题原因: 1.因为helm默认使用k8s的配置文件,默…...

网络安全应急响应预案演练
制定好的应急响应预案,只做培训还不够,还需要通过实战演 练来提高应对网络突发事件的行动力,针对网络突发事件的假想情 景,按照应急响应预案中规定的职责和程序来执行应急响应任务。 根据出现的新的网络攻击手段或其他特殊情况…...
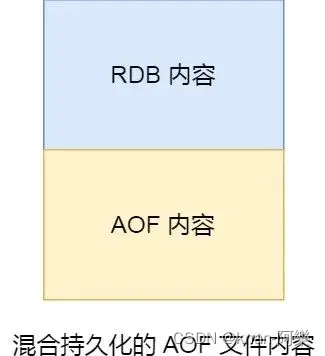
Redis 的混合持久化
RDB 相比于 AOF,数据恢复的速度更快,因为是二进制数据,直接加载进内存即可,但是 RDB 的频率不好把握。 如果频率太低,在两次快照期间服务器发生宕机,可能会丢失较多的数据如果频率太高,频繁写入…...

ElasticSearch总结
ES是什么 ES是一个天生支持分布式的搜索、聚合分析的存储引擎 基于Java开发 基于Lucene的开源分布式搜索引擎 ELK : elasticSearch Logstah Kibana 加入 Beats 后 ELK 改为 :Elastic stack ES解决了什么问题 ES解决的核心问题 : 1.海量数…...
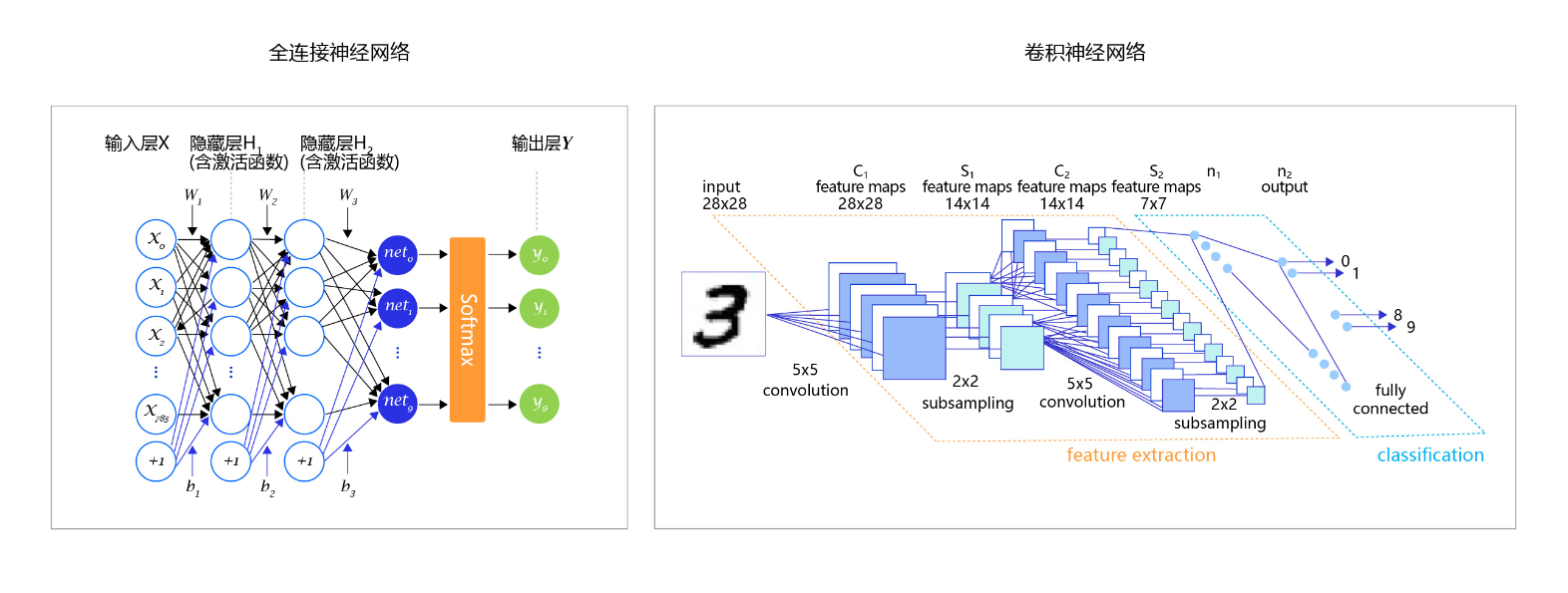
手写数字识别之损失函数
目录 交叉熵 手写数字识别之损失函数 分类任务的损失函数 Softmax函数 交叉熵的简单理解:真实分布与非真实分布的交叉,完全对应,熵为0 交叉熵的代码实现 交叉熵 给定一个策略, 交叉熵就是在该策略下猜中颜色所需要的问题的期望值。更普…...
 和 wait () 有什么区别?)
sleep () 和 wait () 有什么区别?
在Java中,sleep() 和 wait() 是两个用于处理多线程的方法,它们具有不同的作用和用途。 sleep(): sleep() 是 Thread 类的一个静态方法,用于暂停当前线程的执行一段指定的时间。它会阻塞当前线程,不会让其他线程获得执…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
