2023年高教社杯 国赛数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录
- 0 赛题思路
- 1 描述
- 2 问题概括
- 3 建模过程
- 3.1 边界说明
- 3.2 符号约定
- 3.3 分析
- 3.4 模型建立
- 3.5 模型求解
- 4 模型评价与推广
- 5 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 描述
某大学数学系人力资源安排问题是一个整数规划的最优化问题,通过具体分析数学系现有的技术力量和各方面的约束条件,在问题一的求解中,可以列出一天最大直接收益的整数规划,求得最大的直接收益是42860元;而在问题二的求解中,由于教授一个星期只能工作四天,副教授一个星期只能工作五天,在这样的约束条件下,列出一个星期里最大直接收益的整数规划模型,求得其最大直接收益是198720元。
2 问题概括
数学系的教师资源有限,现有四个项目来源于四个不同的客户,工作的难易程度不一,各项目对有关技术人员的报酬不同。所以:
1.在满足工作要求的情况下,如何分配数学系现有的技术力量,使得其一天的直接收益最大?
2.在教授与副教授工作时间受到约束的条件下,如何分配数学系现有的技术力量,使得其在一个星期里的直接收益最大?
3 建模过程
3.1 边界说明
1.不同技术力量的人每天被安排工作的几率是相等的,且相同职称的个人去什么地方工作是随机的;
2.客户除了支付规定的工资额外,在工作期间里,还要支付所有相关的花费(如餐费,车费等);
3.当天工作当天完成.
3.2 符号约定

3.3 分析
由题意可知各项目对不同职称人员人数都有不同的限制和要求.对客户来说质量保证是关键,而教授相对稀缺,因此各项目对教授的配备有不能少于一定数目的限制.其中由于项目技术要求较高,助教不能参加.而两项目主要工作是在办公室完成,所以每人每天有50元的管理费开支.
由以上分析可得:最大直接收益=总收益-技术人员工资-、两地保管费.
3.4 模型建立



3.5 模型求解
相关数据表格如下:
数学系的职称结构及工资情况
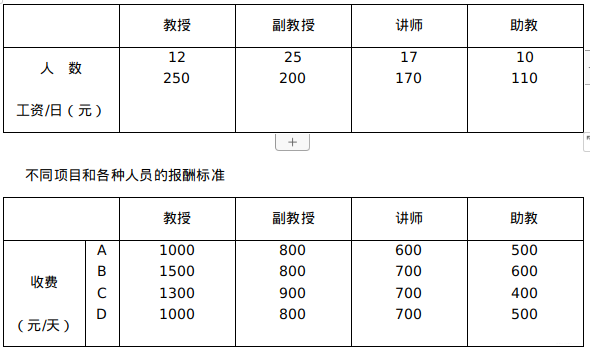
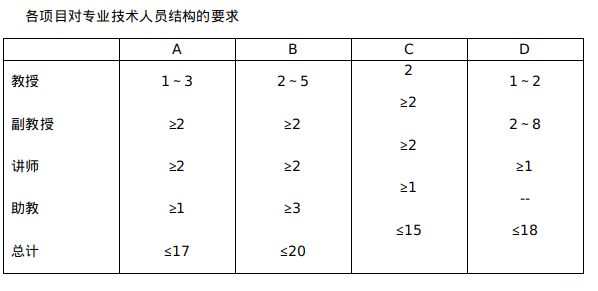
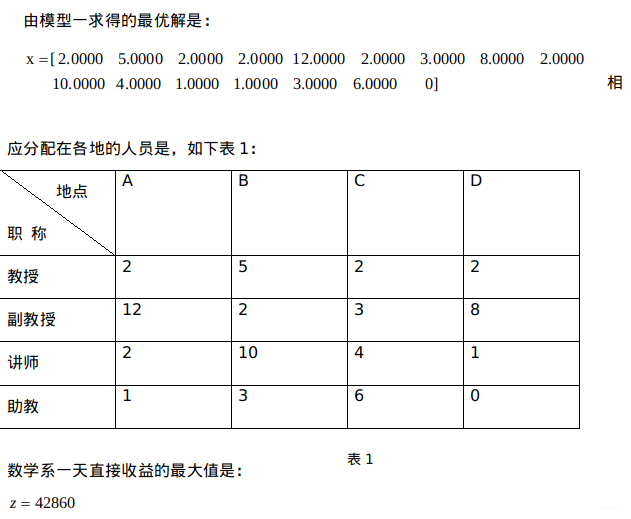
4 模型评价与推广
本模型通过合理的假设,充分考虑各方面的限制条件,得出的人员安排和直接收益
都是本模型的最优解与最优值,对武汉大学数学系的人力资源安排有一定的指导作用。但从模型假设中,我们可以知道对数
学系现有的技术力量的安排是随机的,在相同工作时段里,可能会出现部分人工作次数较多,而部分人较少的不公平情况。
所以在满足工作需求的情况下,分配工作时应该要人为地尽量使得每个人的工作次数不要相差太远,或者相等。
此模型通过对人力资源的调配,从量化的角度得出数学系的最大直接收益。利用此模型的方法可以求出所有类似本模型的线性规划模型。但是,本模型只是单目标的规划,可以在此基础上,增加目标要求。如在数学系的直接收益尽可能大的基础上,使得客户所花费的资金最少,等等。从而建立多目标规划模型。解决更为复杂的实际问题。
5 实现代码
f=[-1000;-800;-550;-450;-1500;-800;-650;-550;-1300;-900;-650;-350;-1000;-800;-650;-450];
A=zeros(9,16);
for i=1:1for j=1:16A(i,j)=1; end
end
for i=2:5for j=i-1:4:11+iA(i,j)=1;end
end
i0=0;
for i=6:9for j=i0+1:(i-5 )*4A(i,j)=1;endi0=j;
end
b=[64;17;20;15;18;12;25;17;10];
Aeq=zeros(1,16);
Aeq(1,3)=1;
beq=[2];
LB=[1;2;2;1;2;2;2;2;2;2;2;1;1;3;1;0];
UB=[3;5;2;2;inf;inf;inf;8;inf;inf;inf;inf;inf;inf;inf;0];
[x,fval]=linprog(f,A,b,Aeq,beq,LB,UB)f=[-1000;-1000;-1000;-1000;-1000;-1000;-1000;-1500;-1500;-1500;-1500;-1500;-1500;-1500;-1250;-1250;-1250;-1250;-1250;-1250;-1250;-950;-950;-950;-950;-950;-950;-950;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-850;-850;-850;-850;-850;-850;-850;-750;-750;-750;-750;-750;-750;-750;-600;-600;-600;-600;-600;-600;-600;-700;-700;-700;-700;-700;-700;-700;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-500;-500;-500;-500;-500;-500;-500;-600;-600;-600;-600;-600;-600;-600;-350;-350;-350;-350;-350;-350;-350;-450;-450;-450;-450;-450;-450;-450];
A=zeros(60,112);
for i=1;1for j=1:112A(i,j)=1;end
end
i0=0;
for i=2:4for j=i0+1:(i-1)*28A(i,j)=1;endi0=j;
end
for i=5:32for j=(i-4):28:80+iA(i,j)=1;end
end
for i=33:39for j= i-32:7:(i-11)A(i,j)=1;end
end
j0=j;
for i=40:46for j=j0+(i-39):7:(i-18)+j0A(i,j)=1;end
end
j0=j;
for i=47:53for j=j0+(i-46):7:j0+(i-25)A(i,j)=1;end
end
j0=j;
for i=54:60for j=j0+(i-53):7:j0+(i-32)A(i,j)=1;end
end
b=[362;48;125;119;17;17;17;17;17;17;17;20;20;20;20;20;20;20;15;15;15;15;15;15;15;18;18;18;18;18;18;18;12;12;12;12;12;12;12;25;25;25;25;25;25;25;17;17;17;17;17;17;17;10;10;10;10;10;10;10];
UB=[3;3;3;3;3;3;3;5;5;5;5;5;5;5;3;3;3;3;3;3;3;2;2;2;2;2;2;2;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;8;8;8;8;8;8;8;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;0;0;0;0;0;0;0];
LB=[1;1;1;1;1;1;1;2;2;2;2;2;2;2;1;1;1;1;1;1;1;1;1;1;1;1;1;1;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;1;1;1;1;1;1;1;1;1;1;1;1;1;1;3;3;3;3;3;3;3;1;1;1;1;1;1;1;0;0;0;0;0;0;0];
Aeq=zeros(7,112);
for i=1:7Aeq(i,i+14)=1;
end
beq=[2;2;2;2;2;2;2];
[x,fval]=linprog(f,A,b,Aeq,beq,LB,UB)
建模资料
资料分享: 最强建模资料


相关文章:

2023年高教社杯 国赛数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录 0 赛题思路1 描述2 问题概括3 建模过程3.1 边界说明3.2 符号约定3.3 分析3.4 模型建立3.5 模型求解 4 模型评价与推广5 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 描述 …...

React内置函数之startTransition与useTransition
React内置函数之startTransition,useTransition 在React中,使用startTransition和useTransition这两个内置函数可以帮助我们更好地管理组件的过渡状态。这两个函数的出现,旨在提供一种简单而强大的方式,来处理组件状态的变化&…...

观察者模式简介
概念: 观察者模式(Observer Pattern)是一种行为型设计模式,用于在对象之间建立一对多的依赖关系,当一个对象的状态发生变化时,其相关依赖对象会自动收到通知并进行相应处理。 特点: 松耦合&a…...

统计程序两个点之间执行的指令数量
环境:支持perf ubuntu安装 apt-get install linux-tools-common linux-tools-generic linux-tools-uname -randroid 一般自带simpleperf 分析 两个点作差, 求中间结果; *(int*)nullptr 0;案例 断点 1 代码 #define SETPOINT(...) do { *(int*)nullptr 0; } while(0…...

时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)
时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价) 目录 时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)预测效果基本介绍程序设计参考资料 预测效果 基本介绍 Matlab实现基于TSO-XGBoost金枪鱼算…...

java- ConcurrentHashMap 并发
1. ConcurrentHashMap 并发 1.1. 减小锁粒度 减小锁粒度是指缩小锁定对象的范围,从而减小锁冲突的可能性,从而提高系统的并发能力。减小锁粒度是一种削弱多线程锁竞争的有效手段,这种技术典型的应用是 ConcurrentHashMap(高性能的 HashMap)…...

java练习8.100m小球落地
题目: 如一个小球从100米高度自由落下,每次落地后就反跳回原高度的一半。 那么求它在第10次落地时,共经过多少米?第10次反弹多高? public static void main(String[] args) {/*假如一个小球从100米高度自由落下,每次落…...

Android JNI系列详解之生成指定CPU的库文件
一、前提 这次主要了解Android的cpu架构类型,以及在使用CMake工具的时候,如何指定生成哪种类型的库文件。 如上图所示,是我们之前使用CMake工具默认生成的四种cpu架构的动态库文件:arm64-v8a、armeabi-v7a、x86、x86_64࿰…...
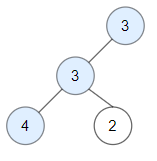
Leetcode每日一题:1448. 统计二叉树中好节点的数目
原题 给你一棵根为 root 的二叉树,请你返回二叉树中好节点的数目。 「好节点」X 定义为:从根到该节点 X 所经过的节点中,没有任何节点的值大于 X 的值。 示例 1: 输入:root [3,1,4,3,null,1,5] 输出:4 解…...

华为OD七日集训第2期 - 按算法分类,由易到难,循序渐进,玩转OD(文末送书)
目录 一、适合人群二、本期训练时间三、如何参加四、7日集训第2期五、精心挑选21道高频100分经典题目,作为入门。第1天、逻辑分析第2天、字符串处理第3天、数据结构第4天、递归回溯第5天、二分查找第6天、深度优先搜索dfs算法第7天、动态规划 六、集训总结1、《代码…...

3d max插件CG MAGIC中的蜂窝材质功能可提升效率吗?
工作中能提升效率也都是大家所想的,对于设计师的一个设计过程中,可能想怎么样可以更快呀,是哪个步骤慢了呢? 这样的结果只能说会很多,但是建模这个步骤,肯定是有多无少的。 为了让模型更加逼真,…...

一句话木马攻击复现:揭示黑客入侵的实战过程
这篇文章旨在用于网络安全学习,请勿进行任何非法行为,否则后果自负。 准备环境 OWASP虚拟机xfp 7与xshell 7 DVWA系统默认的账号密码均为:admin/admin 1、命令注入中复现 攻击payload 127.0.0.1 | echo "<?php eval(…...
【游戏开发教程】Unity Cinemachine快速上手,详细案例讲解(虚拟相机系统 | 新发出品 | 良心教程)
文章目录 一、前言二、插件下载三、案例1:第三人称自由视角,Free Look character场景1、场景演示2、组件参数2.1、CinemachineBrain:核心2.2、CinemachineFreeLook:第三人称自由视角相机2.2.1、设置Follow:跟随2.2.2、…...
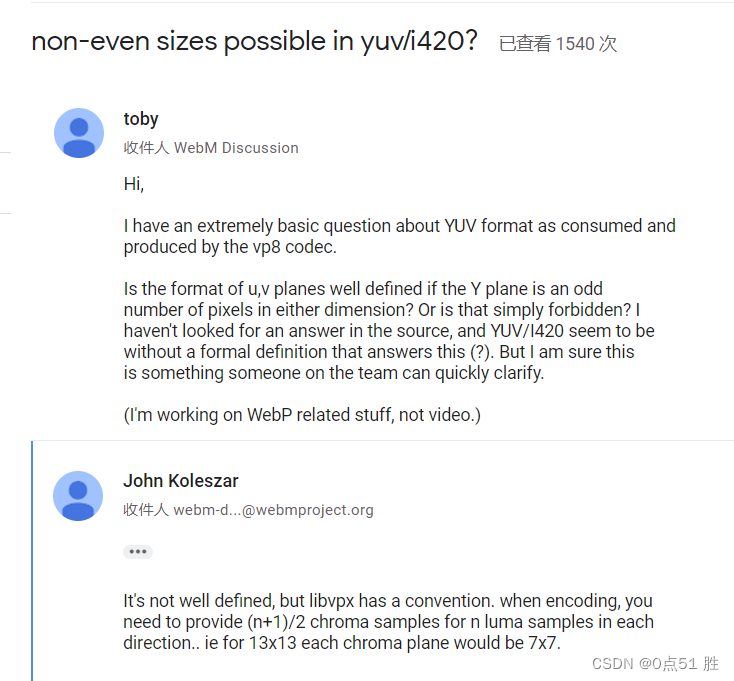
当图像宽高为奇数时,如何计算 I420 格式的uv分量大小
背景 I420 中 yuv 数据存放在3个 planes 中。 网上一般说 I420 数据大小为 widthheight1.5 但是当 width 和 height 是奇数时,这个计算公式会有问题。 I420 中 u 和 v 的宽高分别为 y 的一半。 但是当不能整除时,是如何取整呢?向上还是向下&…...
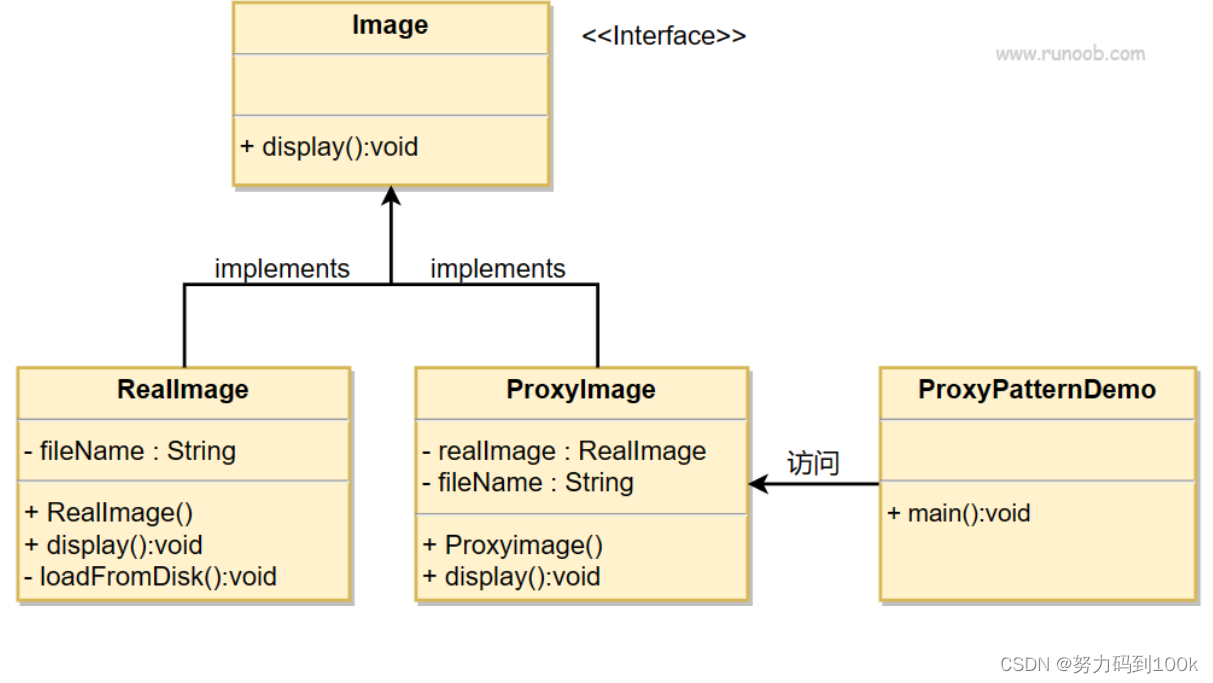
结构型模式-代理模式
代理模式* 定义:在代理模式(Proxy Pattern)中,一个类代表另一个类的功能。这种类型的设计模式属于结构型模式。在代理模式中,我们创建具有现有对象的对象,以便向外界提供功能接口。 意图:为其…...

SpringBoot+Redis BitMap 实现签到与统计功能
最近项目里需要集成签到和统计功能,连续签到后会给用户发放一些优惠券和奖品,以此来吸引用户持续在该品台进行活跃。下面我们一些来聊一聊目前主流的实现方案。 因为签到和统计的功能涉及的数据量比较大,所以在如此大的数据下利用传统的关系…...

P5739 【深基7.例7】计算阶乘
题目描述 求 n ! n! n!,也就是 1 2 3 ⋯ n 1\times2\times3\dots\times n 123⋯n。 挑战:尝试不使用循环语句(for、while)完成这个任务。 输入格式 第一行输入一个正整数 n n n。 输出格式 输出一个正整数,…...
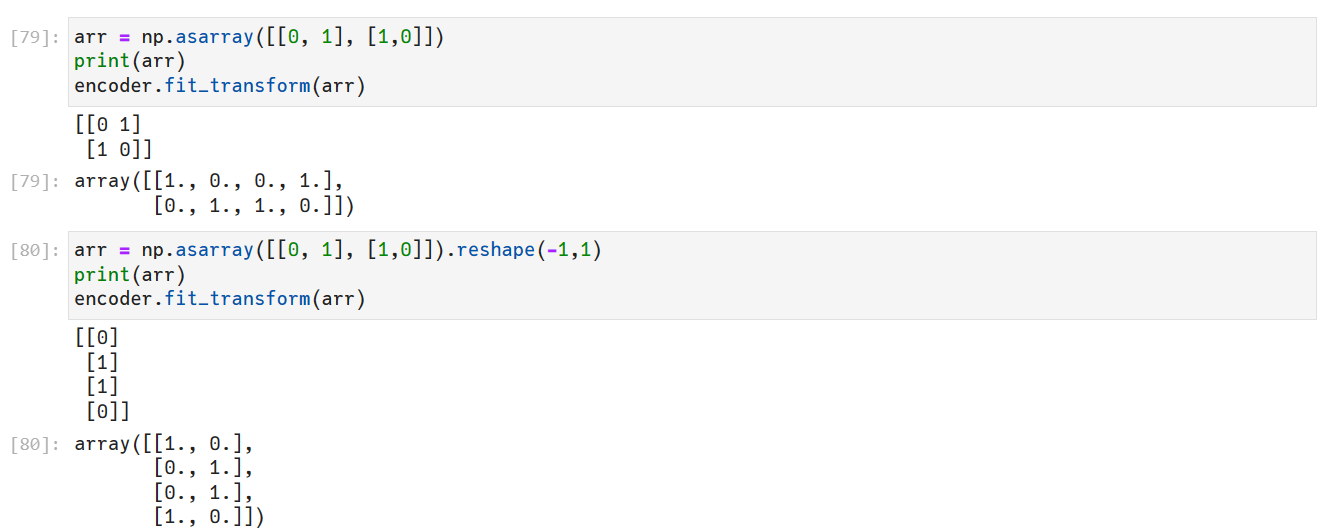
scikit-learn中OneHotEncoder用法
One-Hot编码,又称为一位有效编码,是分类变量作为二进制向量的表示。这首先要求将分类值映射到整数值,然后,每个整数值被表示为二进制向量,将整数索引标记为1,其余都标为0。 OneHotEncoder()常用参数解释 …...
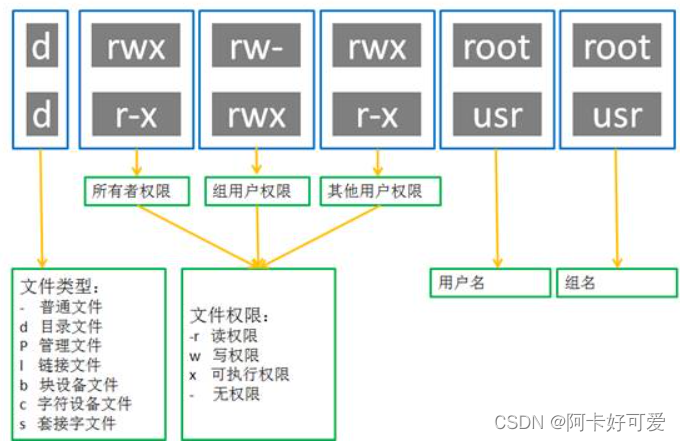
linux操作系统的权限的深入学习(未完)
1.Linux权限的概念 Linux下有两种用户:超级用户(root)、普通用户。 超级用户:可以再linux系统下做任何事情,不受限制 普通用户:在linux下做有限的事情。 超级用户的命令提示符是“#”,普通用户…...
C 连接MySQL8
Linux 安装MySQL 8 请参考文章:Docker 安装MySQL 8 详解 Visual Studio 2022 编写C 连接MySQL 8 C源码 #include <stdio.h> #include <mysql.h> int main(void) {MYSQL mysql; //数据库句柄MYSQL_RES* res; //查询结果集MYSQL_ROW row; //记录结…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...
