k-近邻算法概述,k-means与k-NN的区别对比
目录
k-近邻算法概述
k-近邻算法细节
k值的选取
分类器的决策
k-means与k-NN的区别对比
k-近邻算法概述
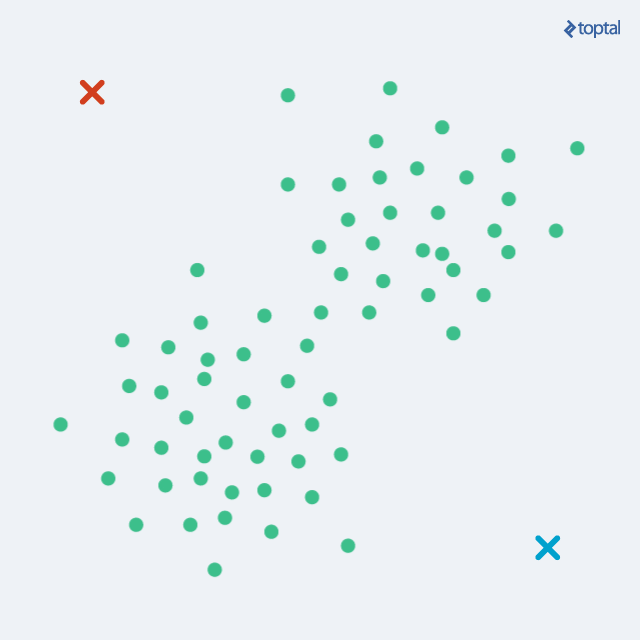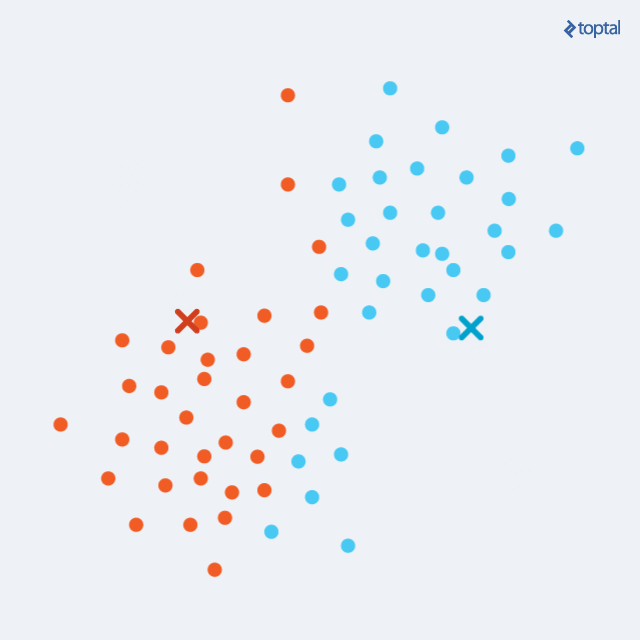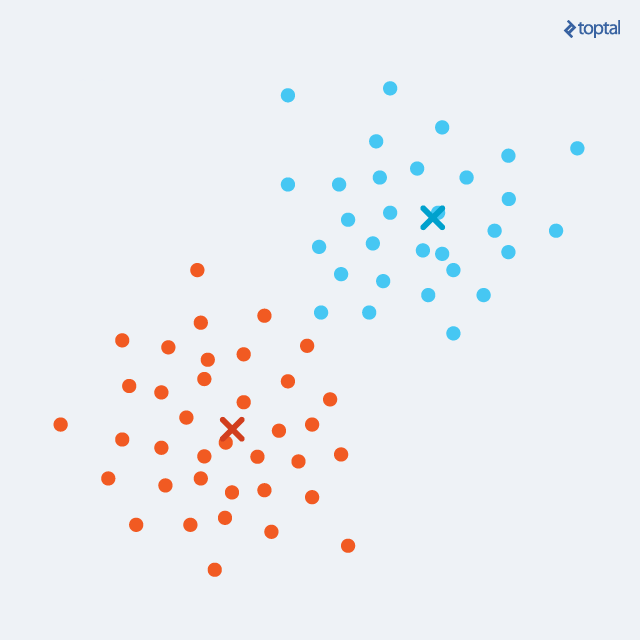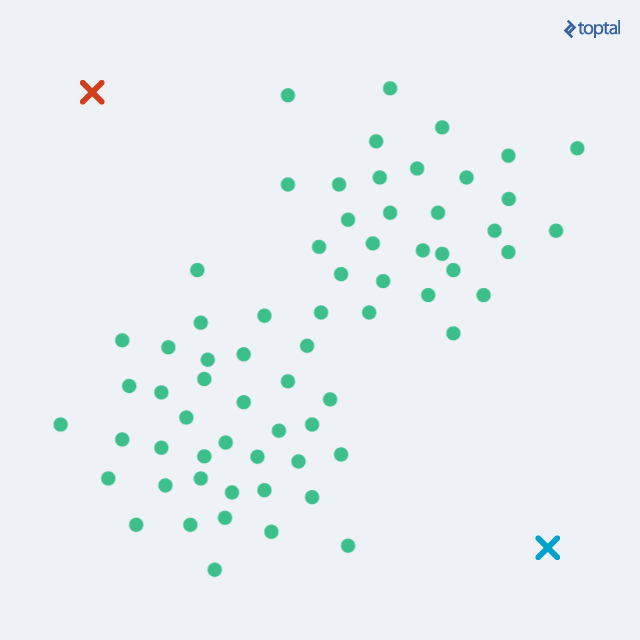
k近邻(k-nearest neighbor, k-NN)算法由 Cover 和 Hart 于1968年提出,是一种简单的分类方法。通俗来说,就是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的 k 个实例,这 k 个实例的多数属于某个类,就把该输入实例分类到这个类中(类似于投票时少数服从多数的思想)。接下来读者来看下引自维基百科上的一幅图:
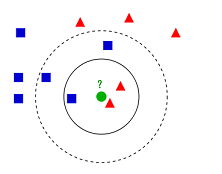
图1:数据
如上图 1 所示,有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所示的数据则是待分类的数据,那它的类别是什么?下面根据 k 近邻的思想来给绿色圆点进行分类。
如果 k=3,绿色圆点的最邻近的 3 个点是 2 个红色小三角形和 1 个蓝色小正方形,根据少数服从多数的思想,判定绿色的这个待分类点属于红色的三角形一类。如果 k=5,绿色圆点最邻近的 5 个邻居是 2 个红色三角形和 3 个蓝色的正方形,根据少数服从多数的思想,判定绿色的这个待分类点属于蓝色的正方形一类。
上面的例子形象展示了 k 近邻的算法思想,可以看出 k 近邻的算法思想非常简单。
k-近邻算法细节
k值的选取
假设有训练数据和待分类点如下图 2,图中有两类,一个是黑色的圆点,一个是蓝色的长方形,待分类点是红色的五边形。根据 k 近邻算法步骤来决定待分类点应该归为哪一类。读者能够看出来五边形离黑色的圆点最近,k 为1,因此最终判定待分类点是黑色的圆点。假设 k=1,那么测试样本的分类结果只受距离最近的一个样本影响,这种情况下模型很容易学习到噪声,出现过拟合。
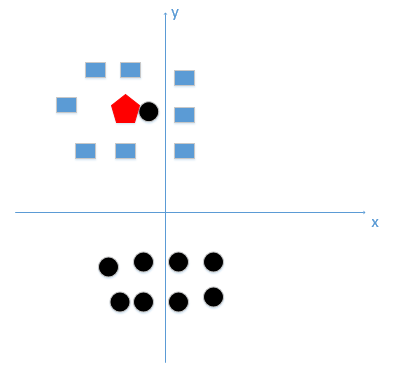
图2:训练数据
明显这样分类是错误的,此时距离五边形最近的黑色圆点是一个噪声,如果 k 太小,分类结果受距离最近的一些样本影响,这种情况下模型很容易学习到噪声,出现过拟合。
如果k大一点,k 等于8,把长方形都包括进来,很容易得到正确的分类应该是蓝色的长方形!如下图:
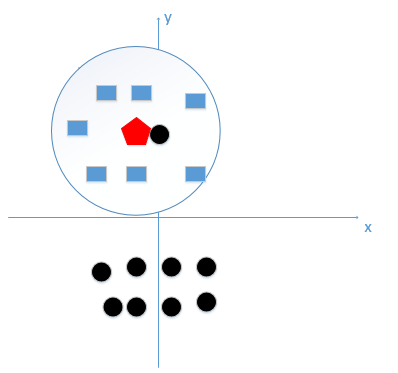
图3:k=8
如果K与训练样本的总数相等,那会出现什么样的分类结果呢?
如果 k=N(N为训练样本的个数),那么无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类。这相当于没有训练模型!直接拿训练数据统计了一下各个数据的类别,找最大的而已!如下图所示:
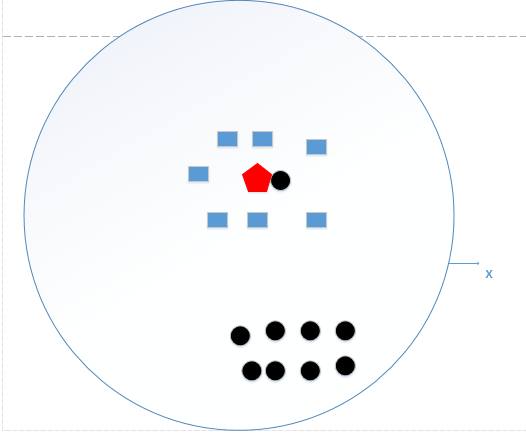
图3:k=N
为了避免出现以上两种极端情况,实践中我们会用到交叉验证,即从 k=1 开始,使用验证集去估计分类器的错误率,然后将 k 依次加1,每次计算分类器的整体错误率,不断重复这个过程,最后就能得到错误率最小的 k 值,这就是我们要找的合适的 k 值。需要注意的是,一般 k 的取值不超过20,并且要尽量取奇数,以避免在最终分类结果中出现样本数相同的两个类别。

分类器的决策
在上面几个例子中,判断待决策样本属于哪一类时,都是根据少数服从多数的思想。为什么根据这种思想做分类决策,背后的原理是什么呢?
假设分类的损失函数为0-1损失函数,分类函数为

k-means与k-NN的区别对比
k-means与k-NN是经常容易被混淆的两个算法,即使是做了多年机器学习的老江湖,也可能嘴瓢或者忘记两个算法的区分。
两种算法之间的根本区别是:
k-means是无监督学习,k-NN是监督学习;
k-means解决聚类问题,k-NN解决分类或回归问题。
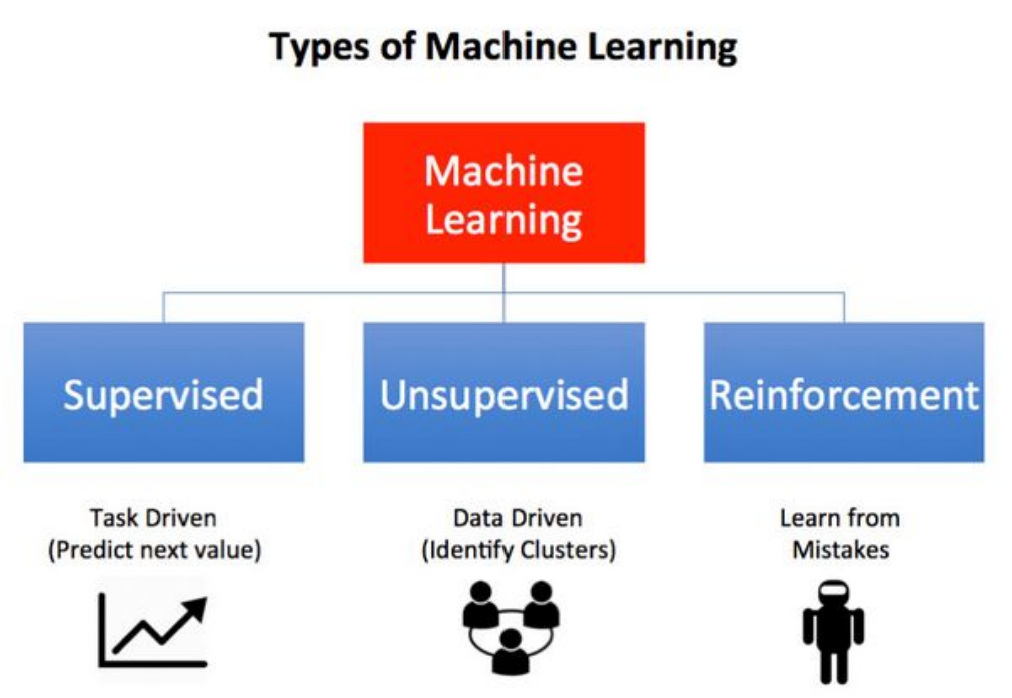
k-means算法把一个数据集分割成簇,使得形成的簇是同构的,每个簇里的点相互靠近
k-NN算法尝试基于其k个(可以是任何数目)周围邻居来对未标记的实例进行分类。
k-means算法的训练过程需要反复的迭代操作(寻找新的质心),但是k-NN不需要。
k-means中的k代表的是簇中心
k-NN的k代表的是选择与测试样本距离最近的前k个训练样本数。
| k-means | k-NN | |
| 学习范式 | 无监督学习算法 | 监督学习算法 |
| 提出时间 | 1967年 | 1968年 |
| 适用问题 | 解决聚类问题 | 解决分类或回归问题 |
| 核心思想 | 物以类聚,人以群分 | 近朱者赤,近墨者黑 |
| 算法原理 | k-means是基于中心的聚类方法,通过迭代,将样本分到k个类中,使得每个样本与其所属类的中心或均值最近;得到k个类别,构成对空间的划分。 | k-NN算法简单、直观,给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最近邻的k个实例,这k个实例的多数属于某个类,就把该输入实例分为这个类。 |
| 算法流程 | k-means聚类的算法是一个迭代过程,每次迭代包括两个步骤。首先选择k个类的中心,将样本逐个指派到与其最近的中心的类中,得到一个聚类结果;然后更新每个类的样本的均值,作为类的新的中心;重复上述步骤,直到收敛为止。 | (1)当有新的测试样本出现时,计算其到训练集中每个数据点的距离;(距离度量) (2)根据距离选择与测试样本距离最小的前k个训练样本;(k值选择) (3)基于这k个训练样本的类别来划分新样本的类别,通常选择这k个训练样本中出现次数最多的标签作为新样本的类别。(决策规则) |
| 算法图示 |
|
|
| k的意义 | k是类的数目 | k是用来计算的相邻数据数 |
| k的选择 | k是类的数目,是人为设定的数字。可以尝试不同的k值聚类,检验各自得到聚类结果的质量,推测最优的k值。聚类结果的质量可以用类的平均直径来衡量。一般地,类别数变小时,平均直径会增加;类别数变大超过某个值以后,平均直径会不变;而这个值正式最优的k值。实验时,可以采用二分查找,快速找到最优的k值。 | k值的选择会对k-NN的结果产生重大影响。 ·如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预测,“学习”的近似误差(approximation error)会减小,只有与输入实例较近的(相似的)训练实例才会对预测结果起作用。但缺点是“学习”的估计误差(estimation error)会增大,预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。换句话说,k值的减小就意味着整体模型变得复杂,容易发生过拟合。 ·如果选择较大的k值,就相当于用较大邻域中的训练实例进行预测。其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时与输入实例较远的(不相似的)训练实例也会对预测起作用,使预测发生错误。k值的增大就意味着整体的模型变得简单。 ·如果k=n,那么无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类。这时,模型过于简单,完全忽略训练实例中的大量有用信息,是不可取的。 ·在应用中,k值一般取一个比较小的数值。通常采用交叉验证法来选取最优的k值。 |
| k与结果 | k值确定后每次结果可能不同,从 n 个数据对象任意选择 k 个对象作为初始聚类中心,随机性对结果影响较大。 | k-NN算法中,当训练集、距离度量(如欧氏距离)、k值和决策规则(如多数表决)确定后,对于任何一个新输入的实例,它所属的类唯一确定。 |
| 复杂度 | 时间复杂度:O(n*k*t),n为训练实例数,k为聚类数,t为迭代次数。 | 线性扫描时间复杂度:O(n) kd树方法时间复杂度:O(logn) |
| 算法特点 | 是基于划分的聚类方法;类别数k事先指定;以欧氏距离平方表示样本之间的距离,以中心或样本的均值表示类别;以样本和其所属类的中心之间的距离的总和为最优化的目标函数;得到的类别是平坦的、非层次化的;算法是迭代算法,不能保证得到全局最优。 | k-NN算法没有显式的学习过程;实现k-NN时,主要考虑问题是如何对训练数据进行快速k近邻搜索。 |
| 算法优点 | 1、解决聚类问题的经典算法,简单、快速; 2、当处理大数据集时,算法保持可伸缩性和高效率; 3、当簇近似为高斯分布时,效果较好; 4、时间复杂度近于线性,适合挖掘大规模数据集。 | 1、对输入数据无假定,如不会假设输入数据是服从正太分布; 2、k-NN可以处理分类问题,同时天然可以处理多分类问题,比如鸢尾花的分类; 3、简单,易懂,同时也很强大,对于手写数字的识别,鸢尾花这一类问题来说,准确率很高; 4、k-NN还可以处理回归问题,也就是预测; 5、对异常值不敏感; 6、可以用于数值型数据,也可以用于离散型数据。 |
| 算法缺点 | 1、类别数k需要事先指定; 2、对初值敏感,即对于不同的初值,可能会导致不同结果; 3、不适合非凸形状的簇或者大小差别很大的簇; 4、对噪声和孤立点敏感; 5、属于启发式算法,不能保证得到全局最优。 | 1、计算复杂度高,线性扫描方法需要计算输入实例与每一个训练实例的距离,当训练集很大时,计算非常耗时;可以通过kd树等方法改进; 2、严重依赖训练样本集,对训练数据的容错性差,如果训练数据集中,有一两个数据是错误的,刚刚好又在需要分类的数值的旁边,就会直接导致预测的数据的不准确; 3、距离度量方法以及k值的选取都有比较大的影响,k值选择不当则分类精度不能保证。 |
| 相似点 | 都包含这样的过程,给定一个点,在数据集中找离它最近的点,即二者都用到了NN(Nearest Neighbor)算法,一般用kd树来实现NN。 | |
相关文章:

k-近邻算法概述,k-means与k-NN的区别对比
目录 k-近邻算法概述 k-近邻算法细节 k值的选取 分类器的决策 k-means与k-NN的区别对比 k-近邻算法概述 k近邻(k-nearest neighbor, k-NN)算法由 Cover 和 Hart 于1968年提出,是一种简单的分类方法。通俗来说,就是给定一个…...

node 项目搭建
1. 初始化项目 cmd 执行 cnpm init -y 创建README.md 依赖安装 1. 数据库 和 框架 mysql express cnpm install mysql express --save 2. 后端跨域 cors cnpm i cors 3. 安装 body-parser 声明引用 用于接收前端 post 过来的数据 cnpm install --save body-parser 4…...
CSS 属性值计算过程
目录 例子1,确定声明值2,层叠冲突2.1,比较源重要性2.2,比较优先级2.3,比较源次序 3,使用继承4,使用默认值其他 例子 我们来举例说明<h1> 标签最终的样式: <div><h1…...

QT版权查询
文章目录 QT工具版权QT模块版权查询 根据条件自动筛选: Qt Features, Framework Essentials, Modules, Tools & Add-Ons QT工具版权 Licensing QT模块版权查询 在 All Modules 中点击进入每个模块,在详细内容中一般有Lisence相关内容。 Licens…...

【leetcode 力扣刷题】双指针///原地扩充线性表
双指针///原地扩充线性表 剑指 Offer 05. 替换空格定义一个新字符串扩充字符串,原地替换思考 剑指 Offer 05. 替换空格 题目链接:剑指 Offer 05. 替换空格 题目内容: 这是一道简单题,理解题意,就是将字符串s中的空格…...

第八章,帖子列表
8.1添加帖子列表 <script> import { mapState } from vuex . . . </script> computed: {...mapState([auth,user,articles]) }, <Message :sh...

netty与websockt实现聊天
配置websockt: import lombok.Data; import org.springframework.boot.context.properties.ConfigurationProperties; import org.springframework.context.annotation.Configuration;/*** websocket配置*/ Data Configuration ConfigurationProperties(prefix &qu…...
21.2 CSS 三大特性与页面布局
1. 开发者工具修改样式 使用开发者工具修改样式, 操作步骤如下: * 1. 打开开发者工具: 在浏览器中右键点击页面, 然后选择检查或者使用快捷键(一般是 F12 或者 CtrlShiftI)来打开开发者工具.* 2. 打开样式编辑器: 在开发者工具中, 找到选项卡或面板, 一般是Elements或者Elemen…...

MySQL 特殊语法时间格式以及Greadb连接
一、时间语法 DATE_FORMAT和to_char() select to_char(now(),%Y-%m-%d %H:%i:%s) from dual; select DATE_FORMAT(now(),%Y-%m-%d %H:%i:%s) from dual; 2.to_date() 和STR_TO_DATE(#{date},%Y-%m-%d ) select to_date(now(),yyyy-mm-dd hh24:mi:ss) from dual;...
Python(.pyc)反编译:pycdc工具安装与使用
本文将介绍如何将python的.pyc文件反编译成源码,以便我们对源码的学习与改进。pycdc工具安装 下载地址: 1、Github地址:https://github.com/zrax/pycdc ,下载后需要使用CMake进行编译。 2、已下载好及编译好的地址:ht…...
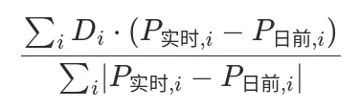
山西电力市场日前价格预测【2023-08-28】
日前价格预测 预测明日(2023-08-28)山西电力市场全天平均日前电价为319.70元/MWh。其中,最高日前电价为371.80元/MWh,预计出现在19: 15。最低日前电价为278.59元/MWh,预计出现在13: 00。 价差方向预测 1: …...

python3/pip3 SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed
环境: mac os 背景: 电脑之前安装的是python3.9 , 现在升级到python3.10。 从python官网下载macos版本的python3.10 pkg。 双击安装。 程序使用aiohttp访问ebay 。 出错: aiohttp.client_exceptions.ClientConnectorCertifi…...

Python中的迭代器与生成器
文章目录 1、迭代器2、生成器3、列表推导式和生成器表达式4、enumerate() 在Python中,迭代器(Iterator)和生成器(Generator)是两种用于处理可迭代对象的重要工具。而可迭代对象包括列表,元组,字…...
简单着色器编写(下)
函数部分介绍完了,最后来介绍一下main函数中的部分。 std::string vertexShader "#version 330 core\n" "\n" "layout(location0)in vec4 position;" "\n" "void main()\n" "{\n&…...

go并发编程基础
go并发编程 1waitgroup WaitGroup就是等待所有的goroutine全部执行完毕,add方式和Down方法要配套使用 package mainimport ("fmt""sync" )func main() {var wq sync.WaitGroupwq.Add(100) //监控多少个goroutine执行结束for i: 0;i<100;…...

PHP之 导入excel表格时,获取日期时间变成浮点数
读取到的时间 float(0.20833333333333) 原格式 15:00:00 代码 if (Request::isPost()) {$file_url input(upfile); // 本地上传文件地址// 读取文件内容$local_file_url __dir__./../../../public.$file_url;// $spreadsheet new Spreadsheet();// $sheet $spreadsheet-…...

学习 Java 报表技术导入 Maven 依赖出错:jacob 无法下载、jasperreports 依赖错误
发生缘由 最近在做一个可视化项目,用到了 Java 报表技术。在跟着「黑马」课程导入 pom.xml 文件的时候提示下载依赖错误。 com.jacob 包无法下载Failed to read artifact descriptor for com.lowagie:itext:jar:2.1.7.js6 运行环境 电脑系统版本:Win…...

力扣-哈希-最长连续序列
题目 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1: **输入:**nums [100,4,200,1,3,2] **输出&a…...

Java线程 - 详解(1)
一,创建线程 方法一:继承Thread类 class MyThread extends Thread{Overridepublic void run() {System.out.println("线程1");} }public class Test {public static void main(String[] args) {MyThread myThread new MyThread();myThread.…...
)
结构体-C语言(初阶)
目录 一、结构体声明 1.1 结构概念 1.2 结构声明 1.3 结构成员的类型 1.4 结构体变量的定义和初始化 二、结构体成员的访问 2.1 结构体变量访问成员 2.2 结构体指针访问指向变量的成员 三、结构体传参 一、结构体声明 1.1 结构概念 结构是一些值的集合,这些值称为…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...