Harbour.Space Scholarship Contest 2023-2024 (Div. 1 + Div. 2) A ~ D
比赛链接
A

正常枚举就行,从最后一位往前枚举,-1、-2、-3...这样
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 1010;int a[N];void solve()
{int x, y, n;cin >> x >> y >> n;a[1] = x, a[n] = y;int res = 1;for(int i = n - 1; i >= 1; i --){a[i] = a[i + 1] - res;res ++;}if(a[1] < x){cout << -1 << endl;return;}a[1] = x;for(int i = 1; i <= n; i ++)cout << a[i] << ' ';cout << endl;
}int main()
{IOSint _;cin >> _;while(_ --){solve();}return 0;
}B

第一个操作可以做到把所有在奇数位的字母任意排列以及把所有在偶数位的字母任意排列。
第二个操作,如果k是奇数时没有任何影响,只用第一种情况就能最优;如果k是偶数时,而且k又小于n,每次操作可以做到奇偶对调,就可以实现任意排序。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;void solve()
{int n, k;cin >> n >> k;string A, B;string s;cin >> s;for(int i = 0; i < s.size(); i ++){if(i % 2)B.push_back(s[i]);else A.push_back(s[i]);}sort(A.begin(), A.end());sort(B.begin(), B.end());sort(s.begin(), s.end());if(k % 2){n = (n + 1) / 2;for(int i = 0; i < n; i ++){if(i < A.size())cout << A[i];if(i < B.size())cout << B[i];}}else cout << s;cout << endl;
}int main()
{IOSint _;cin >> _;while(_ --){solve();}return 0;
}C

可以先把x变成2的i次方,在这个过程中用2的i次方减,一个数一定可以由若干2的i的方组成,x到2的i次方过程中减掉数的总和也一定可以由若干2的i次方组成。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;ll a[50];
bool st[50];void solve()
{vector<int> ans;int x;cin >> x;int l = 1, r = 32;while(l < r){int mid = l + r + 1 >> 1;if(a[mid] <= x)l = mid;else r = mid - 1;}if(a[l] == x){while(x != 1){ans.push_back(x);x >>= 1;}ans.push_back(1);cout << ans.size() << endl;for(int i = 0; i < ans.size(); i ++){cout << ans[i] << ' ';}cout << endl;return;}memset(st, false, sizeof st);while(x > a[l]){int tmp = x - a[l];int L = 1, R = 32;while(L < R){int mid = L + R + 1 >> 1;if(a[mid] <= tmp)L = mid;else R = mid - 1;}for(int i = L; i >= 0; i --){if(st[i])continue;if(x % a[i] == 0){ans.push_back(x);x -= a[i];st[i] = true;break;}}}while(x != 1){ans.push_back(x);x >>= 1;}ans.push_back(1);cout << ans.size() << endl;for(int i = 0; i < ans.size(); i ++){cout << ans[i] << ' ';}cout << endl;return;
}int main()
{IOSa[0] = 1;for(int i = 1; i <= 40; i ++)a[i] = a[i - 1] * 2;int _;cin >> _;while(_ --){solve();}return 0;
}D

这题有点dp那味儿了,总的来说应该是前缀和,太久没写题手生了,写了一个多小时www
看那个公式画个图可以看出来它可以将一个点往下沿等腰三角形延伸,三角形区域内的点都要转换。
可以发现最上面那层有多少个1这一层肯定就要转换多少次,转换完后看第二层也类似,第二层有多少个需要转换的点这一层就要转换多少次,所以一定需要遍历一遍,往后以此类推。所以其实就是从第一层到最后一层遍历一遍所有点,遇到一个需要执行操作的点答案就加一。
现在复杂度已经到达n方了,我们需要想一个O(1)或者logn的算法来计算每个点需不需要转换,然后想到了前缀和,然后加一个额外的二维数组来统计每个点上方的等腰三角形区域内有多少个点被执行过操作。
然后前缀和转化成斜着的,同样是记录有多少个点被执行过操作。一个从左上到右下的斜前缀和数组,一个从右上到左下的斜前缀和数组。
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;const int N = 3010;int n;
char s[N][N];
int a[N][N], dg[N][N], udg[N][N];void solve()
{cin >> n;for(int i = 0; i <= n + 1; i ++)for(int j = 0; j <= n + 1; j ++)a[i][j] = dg[i][j] = udg[i][j] = 0;for(int i = 1; i <= n; i ++)cin >> s[i] + 1;int ans = 0;for(int i = 1; i <= n; i ++){for(int j = 1; j <= n; j ++){a[i][j] = a[i - 1][j] + dg[i - 1][j - 1] + udg[i - 1][j + 1];int tmp = a[i][j] + s[i][j] - '0';if(tmp % 2){ans ++;a[i][j] ++;dg[i][j] ++;udg[i][j] ++;}dg[i][j] += dg[i - 1][j - 1];udg[i][j] += udg[i - 1][j + 1];}}cout << ans << endl;
}int main()
{IOSint _;cin >> _;while(_ --){solve();}return 0;
}相关文章:

Harbour.Space Scholarship Contest 2023-2024 (Div. 1 + Div. 2) A ~ D
比赛链接 A 正常枚举就行,从最后一位往前枚举,-1、-2、-3...这样 #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define endl \nusing namespace std;typedef pair<int, int> PII; typedef long l…...
[管理与领导-53]:IT基层管理者 - 8项核心技能 - 8 - 持续改进
前言: 管理者存在的价值就是制定目标,即目标管理、通过团队(他人)拿到结果。 要想通过他人拿到结果: (1)目标:制定符合SMART原则的符合业务需求的目标,团队跳一跳就可以…...
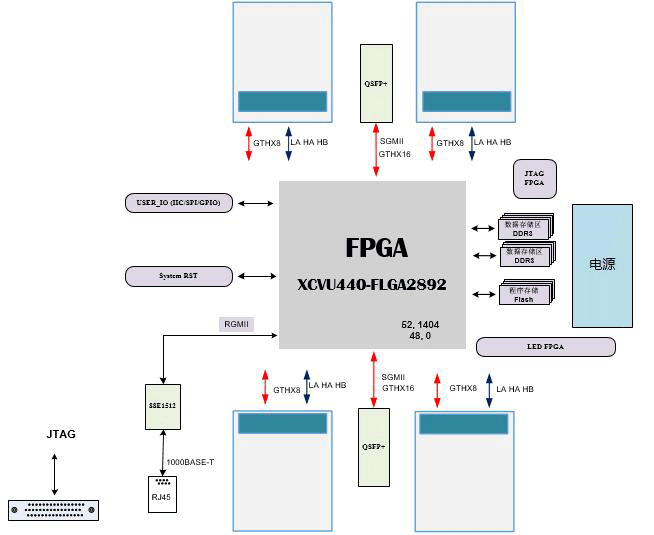
芯片验证板卡设计原理图:446-基于VU440T的多核处理器多输入芯片验证板卡
基于VU440T的多核处理器多输入芯片验证板卡 一、板卡概述 基于XCVU440-FLGA2892的多核处理器多输入芯片验证板卡为实现网络交换芯片的验证,包括四个FMC接口、DDR、GPIO等,北京太速科技芯片验证板卡用于完成甲方的芯片验证任务,多任务…...

几个nlp的小任务(机器翻译)
几个nlp的小任务(机器翻译) 安装依赖库数据集介绍与模型介绍加载数据集看一看数据集的样子评测测试数据预处理测试tokenizer处理目标特殊的token预处理函数对数据集的所有数据进行预处理微调预训练模型设置训练参数需要一个数据收集器,把处理好数据喂给模型设置评估方法参数…...
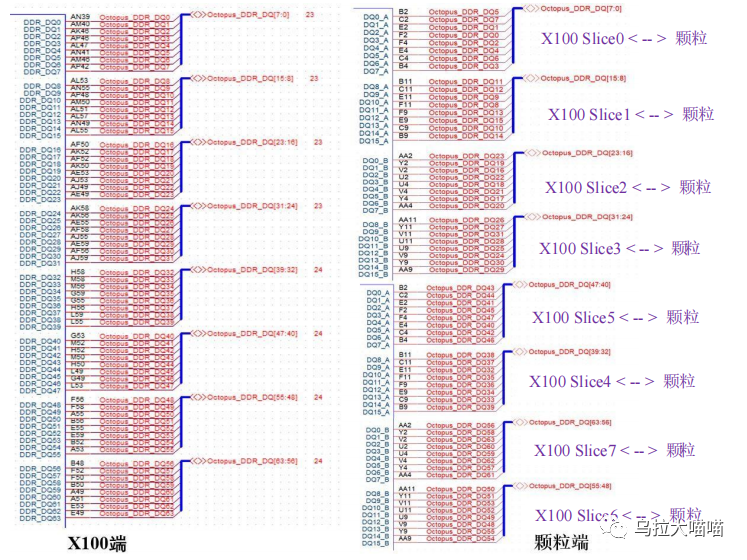
飞腾X100 LPDDR颗粒线序配置辅助工具
B站讲解视频: 正文内容: 一、 飞腾X100显存使用LPDDR4时,需要工程师在X100的固件中去配置线序交换说明,就类似下面这个: 图1 我们需要输入每个slice中DQ的线序,也需要输入slice之间的交换关系,这个工作量也不小,同时容易出现错误,所以开发了一款辅助小工具,…...
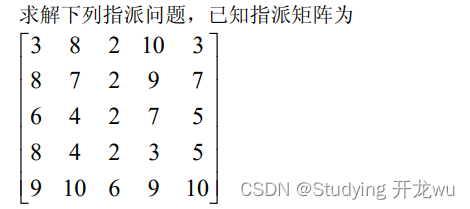
二、数学建模之整数规划篇
1.定义 2.例题 3.使用软件及解题 一、定义 1.整数规划(Integer Programming,简称IP):是一种数学优化问题,它是线性规划(Linear Programming,简称LP)的一个扩展形式。在线性规划中&…...

C语言日常刷题 4
文章目录 题目答案与解析123456 题目 1、设变量已正确定义,以下不能统计出一行中输入字符个数(不包含回车符)的程序段是( ) A: n0;while(chgetchar()!‘\n’)n; B: n0;while(getchar()!‘\n’)n; C: for(n0;getchar()…...
MyBatis plus 多数据源实现
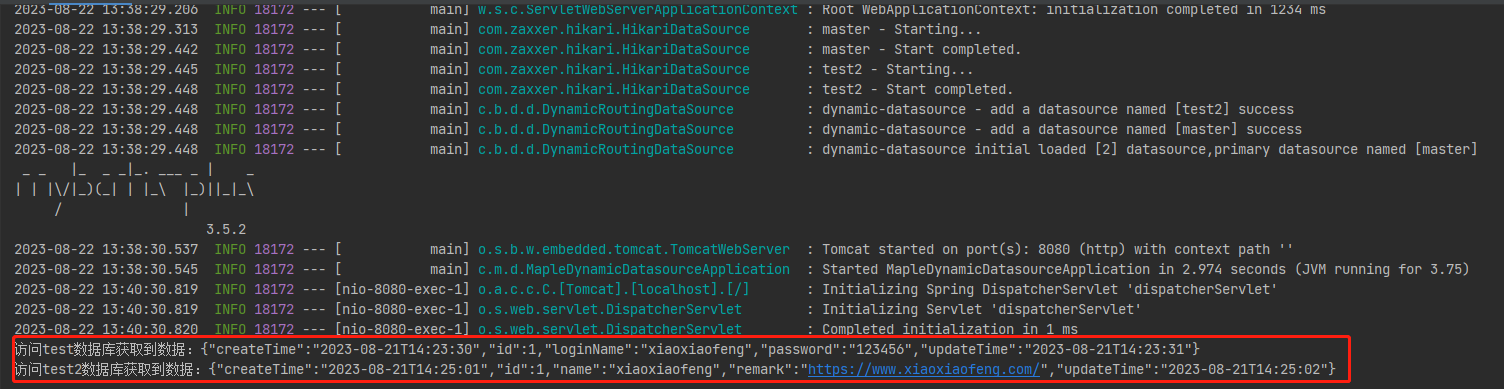
1. 项目背景 最近写文章发布到【笑小枫】小程序和我的个人网站上,因为个人网站用的是halo框架搭建,两边数据结构不一致,导致我每次维护文章都需要两边维护,这就很烦~ 于是,本文就诞生了。通过项目连接这两个数据库&a…...

k-近邻算法概述,k-means与k-NN的区别对比
目录 k-近邻算法概述 k-近邻算法细节 k值的选取 分类器的决策 k-means与k-NN的区别对比 k-近邻算法概述 k近邻(k-nearest neighbor, k-NN)算法由 Cover 和 Hart 于1968年提出,是一种简单的分类方法。通俗来说,就是给定一个…...

node 项目搭建
1. 初始化项目 cmd 执行 cnpm init -y 创建README.md 依赖安装 1. 数据库 和 框架 mysql express cnpm install mysql express --save 2. 后端跨域 cors cnpm i cors 3. 安装 body-parser 声明引用 用于接收前端 post 过来的数据 cnpm install --save body-parser 4…...
CSS 属性值计算过程
目录 例子1,确定声明值2,层叠冲突2.1,比较源重要性2.2,比较优先级2.3,比较源次序 3,使用继承4,使用默认值其他 例子 我们来举例说明<h1> 标签最终的样式: <div><h1…...

QT版权查询
文章目录 QT工具版权QT模块版权查询 根据条件自动筛选: Qt Features, Framework Essentials, Modules, Tools & Add-Ons QT工具版权 Licensing QT模块版权查询 在 All Modules 中点击进入每个模块,在详细内容中一般有Lisence相关内容。 Licens…...

【leetcode 力扣刷题】双指针///原地扩充线性表
双指针///原地扩充线性表 剑指 Offer 05. 替换空格定义一个新字符串扩充字符串,原地替换思考 剑指 Offer 05. 替换空格 题目链接:剑指 Offer 05. 替换空格 题目内容: 这是一道简单题,理解题意,就是将字符串s中的空格…...

第八章,帖子列表
8.1添加帖子列表 <script> import { mapState } from vuex . . . </script> computed: {...mapState([auth,user,articles]) }, <Message :sh...

netty与websockt实现聊天
配置websockt: import lombok.Data; import org.springframework.boot.context.properties.ConfigurationProperties; import org.springframework.context.annotation.Configuration;/*** websocket配置*/ Data Configuration ConfigurationProperties(prefix &qu…...
21.2 CSS 三大特性与页面布局
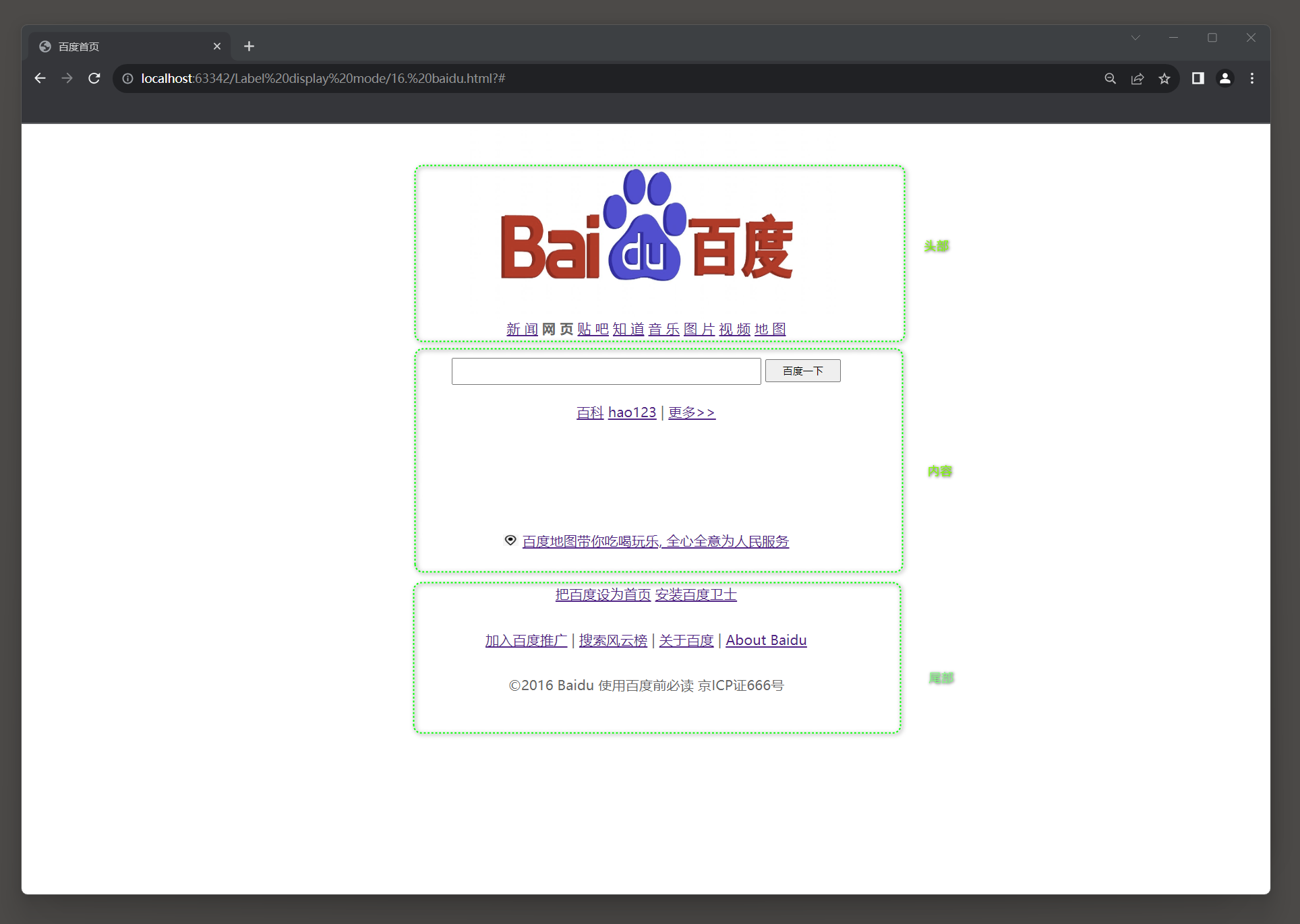
1. 开发者工具修改样式 使用开发者工具修改样式, 操作步骤如下: * 1. 打开开发者工具: 在浏览器中右键点击页面, 然后选择检查或者使用快捷键(一般是 F12 或者 CtrlShiftI)来打开开发者工具.* 2. 打开样式编辑器: 在开发者工具中, 找到选项卡或面板, 一般是Elements或者Elemen…...

MySQL 特殊语法时间格式以及Greadb连接
一、时间语法 DATE_FORMAT和to_char() select to_char(now(),%Y-%m-%d %H:%i:%s) from dual; select DATE_FORMAT(now(),%Y-%m-%d %H:%i:%s) from dual; 2.to_date() 和STR_TO_DATE(#{date},%Y-%m-%d ) select to_date(now(),yyyy-mm-dd hh24:mi:ss) from dual;...
Python(.pyc)反编译:pycdc工具安装与使用
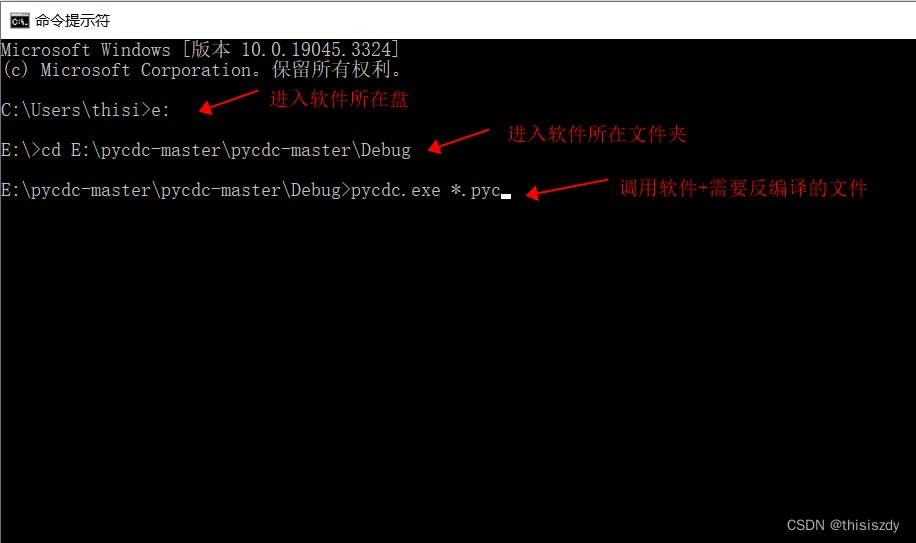
本文将介绍如何将python的.pyc文件反编译成源码,以便我们对源码的学习与改进。pycdc工具安装 下载地址: 1、Github地址:https://github.com/zrax/pycdc ,下载后需要使用CMake进行编译。 2、已下载好及编译好的地址:ht…...
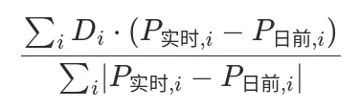
山西电力市场日前价格预测【2023-08-28】
日前价格预测 预测明日(2023-08-28)山西电力市场全天平均日前电价为319.70元/MWh。其中,最高日前电价为371.80元/MWh,预计出现在19: 15。最低日前电价为278.59元/MWh,预计出现在13: 00。 价差方向预测 1: …...

python3/pip3 SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed
环境: mac os 背景: 电脑之前安装的是python3.9 , 现在升级到python3.10。 从python官网下载macos版本的python3.10 pkg。 双击安装。 程序使用aiohttp访问ebay 。 出错: aiohttp.client_exceptions.ClientConnectorCertifi…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
