搜索二叉树的算法解析与实例演示

目录
- 一.搜索二叉树的特性与实现
- 1.特点
- 2.实现
- 二.搜索二叉树的性能
一.搜索二叉树的特性与实现
1.特点
二叉搜索树是特殊的二叉树,它有着更严格的数据结构特点:
(1)非空左子树的所有键值小于其根结点的键值。
(2)非空右子树的所有键值大于其根结点的键值。
(3)左、右子树都是二叉搜索树
如下图所示就是一株典型的搜索二叉树:
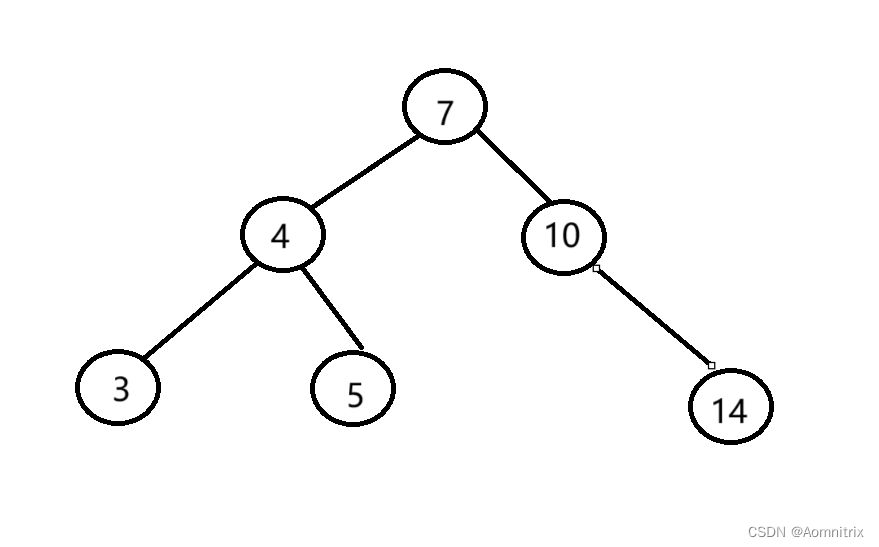
这种结构中序遍历的结果是升序的,以上特性可以帮助我们解决很多问题。例如查找
2.实现
搜索二叉树的查找功能逻辑较简单,根据要查找的值依次与当前节点键值比较,如果小于就在左树继续寻找反之在右树查找。
bool find(const T& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->left;}else if (cur->_key < key){cur = cur->right;}else{return true;}}return false;}
插入功能首先要查找到要插入的值应该放的地方,接着判断自己是父节点的左树还有右树然后进行插入,当查找到与要插入的值相同的键值时,插入失败,因为搜索二叉树不允许有相同的值存在,需要注意的是当此树为空树时,直接插入值即可:
bool Insert(const T& key){if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parents = nullptr;while (cur){if (cur->_key < key){parents = cur;cur = cur->right;}else if (cur->_key > key){parents = cur;cur = cur->left;}else{return false;}}cur = new Node(key);if (parents->_key > key ){parents->left = cur;}else{parents->right = cur;}return true;}
需要重点理解是接下来的删除功能:要删除某个键值 首先需要找到这个结点,大体逻辑与find功能相似,不同的是在找到时如何删除这个结点。这时候分为三种情况:结点左子树为空/结点右子树为空/左右子树都不为空。左或右子树为空时逻辑较简单使用托孤法即可,首先判断是否为根节点如果是则直接将根节点赋值为根节点的右或左结点接着判断自己是父节点的左/右结点,接着让父节点的左/右直接指向我的左或右结点。 当左右子树都不为空时需要使用到替换法,将要删除的结点与左子树的最大结点的键值或者右子树的最小节点的键值替换(因为要保证搜索二叉树的特性),之后删除即可。
bool Erase(const T& key){Node* cur = _root;Node* parents = nullptr;if (cur == nullptr)return false;while (cur){if (cur->_key > key){parents = cur;cur = cur->left;}else if (cur->_key < key){parents = cur;cur = cur->right;}else{if (cur->left == nullptr){ if (cur == _root){_root = cur->right;}else{if (parents->left == cur){parents->left = cur->right;}else{parents->right = cur->right;}}}else if (cur->right == nullptr){if (cur == _root){_root = cur->left;}else{if (parents->left == cur){parents->left = cur->left;}else{parents->right = cur->left;}}}else//左子树和右子树都不为空{Node* parents = cur;Node* leftmax = cur->left;while (leftmax->right){parents = leftmax;leftmax = leftmax->right;}swap(cur->_key, leftmax->_key);if (parents->left == leftmax){parents->left = leftmax->left;}else{parents->right = leftmax->left;}cur = leftmax;}delete cur;return true;}}return false;}
以上讲解的是非递归版的实现,递归版的查找 插入 删除代码更为简洁,但是更难理解。
因为在类外调用成员函数无法向函数传参成员变量,所以在类中进行一些封装:
public:bool findR(const T& key){return _findR(_root, key);}private:bool _findR(Node* root, const T& key){if (root == nullptr){return false;}if (root->_key > key){return _findR(root->left, key);}else if (root->_key < key){return _findR(root->right.key);}else{return true;}}查找与删除功能同样使用了封装:
public:bool InsertR(const T& key){return _InsertR(_root, key);}bool EraseR(const T& key){return _EraseR(_root, key);}private:bool _EraseR(Node*& root, const T& key){if (root == nullptr){return false;}if (root->_key > key){return _EraseR(root->left, key);}else if (root->_key < key){return _EraseR(root->right,key);}else{Node* del = root;if (root->left == nullptr){root = root->right;}else if (root->right == nullptr){root = root->left;}else{Node* leftMax = root->left;while (leftMax->right){leftMax = leftMax->right;}swap(root->_key, leftMax->_key);return _EraseR(root->left, key);}delete del;return true;}}bool _InsertR(Node*& root, const T& key){if (root == nullptr){root = new Node(key);//神之一手return true;}if (root->_key > key){return _InsertR(root->left, key);}else if (root->_key < key){return _InsertR(root->right.key);}else{return false;}}
二.搜索二叉树的性能
查找的性能在搜索二叉树为完全二叉树或者满二叉树或者接近时,时间复杂度是logN,
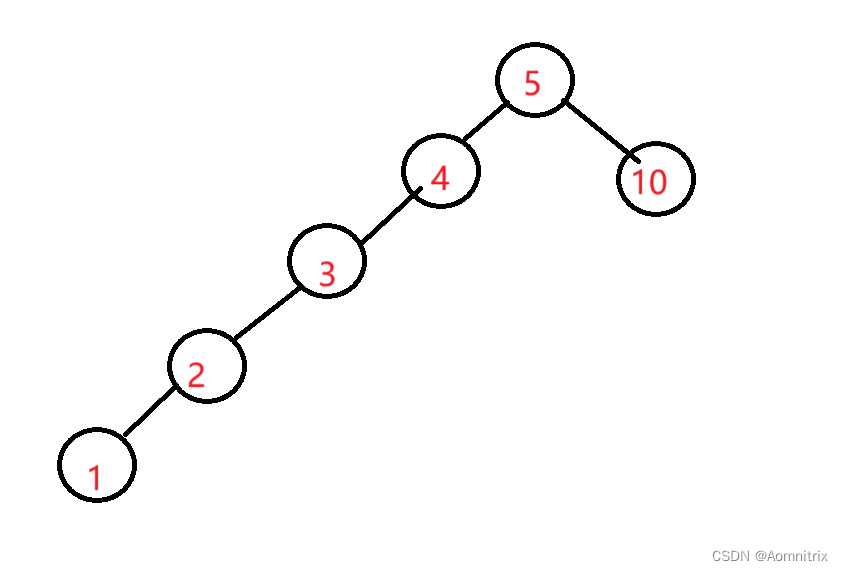
在极端情况下,时间复杂度平均为N/2.
相关文章:

搜索二叉树的算法解析与实例演示
目录 一.搜索二叉树的特性与实现1.特点2.实现二.搜索二叉树的性能 一.搜索二叉树的特性与实现 1.特点 二叉搜索树是特殊的二叉树,它有着更严格的数据结构特点: (1)非空左子树的所有键值小于其根结点的键值。 (2&…...

研磨设计模式day13组合模式
目录 场景 不用模式实现 代码实现 有何问题 解决方案 代码改造 组合模式优缺点 思考 何时选用 场景 不用模式实现 代码实现 叶子对象 package day14组合模式;/*** 叶子对象*/ public class Leaf {/*** 叶子对象的名字*/private String name "";/**…...
之zip)
Linux命令(73)之zip
linux命令之zip 1.zip介绍 linux命令zip是用来压缩文件及解压缩文件名称后缀为".zip"的文件 2.zip用法 zip [参数] filename[.zip] zip常用参数 参数说明-r压缩递归处理-d从压缩文件内删除指定的文件-T检查备份文件是否正确无误-u更换较新的文件到压缩文件内-q不…...

深入理解Reactor模型的原理与应用
1、什么是Reactor模型 Reactor意思是“反应堆”,是一种事件驱动机制。 和普通函数调用的不同之处在于:应用程序不是主动的调用某个 API 完成处理,而是恰恰相反,Reactor逆置了事件处理流程,应用程序需要提供相应的接口并…...

微信小程序开发的投票评选系统设计与实现
摘要 越来越多信息化融入到我们生活当中的同时,也在改变着我们的生活和学习方式,当然,变化最明显的除了我们普通民众之外,要数高校学生的生活方式以及校园信息化的变革。智慧是改变生活和生产的一种来源,那么智慧的体…...

【校招VIP】算法考点之堆排
考点介绍: 排序算法属于数据结构和算法的基础内容,并且也是大厂笔试中的高频考点。 堆排序是使用一棵树存储序列这个课树只保证跟节点是这棵树中的最小值,但并不保证其他节点是按顺序的。因此他的排序是每次从堆中取得堆顶,取得 n…...
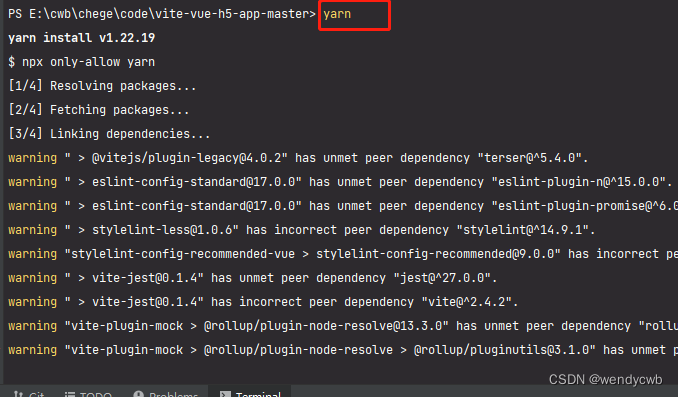
关于yarn安装时报“node“ is incompatible with this module的解决办法
前提: 在用vue写一个h5页面时,当在用yarn安装时,提示如下错误: The engine “node” is incompatible with this module. Expected version "^14.18.0 || ^16.14.0 || >18. 解决办法 我是使用命令忽略错误:…...

开源利器推荐:美团动态线程池框架的接入分享及效果展示
前言 蛮早前有些过关于线程池的使用及参数的一些参考配置,有兴趣的可以翻看以前的博文,但终究无法解决线程池的动态监控和实时修改。 以前读过美团早期发布的动态线程池框架的思路相关文章,但想要独自实现不是一件容易的事。 去年,…...

Linux目录结构与文件管理 (02)(四)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、查看文件内容 二、创建文件 三、删除文件 四、 移动文件 五、复制文件 六、编辑文件内容 总结 前言 今天是在昨天的基础上继续学习,主要…...
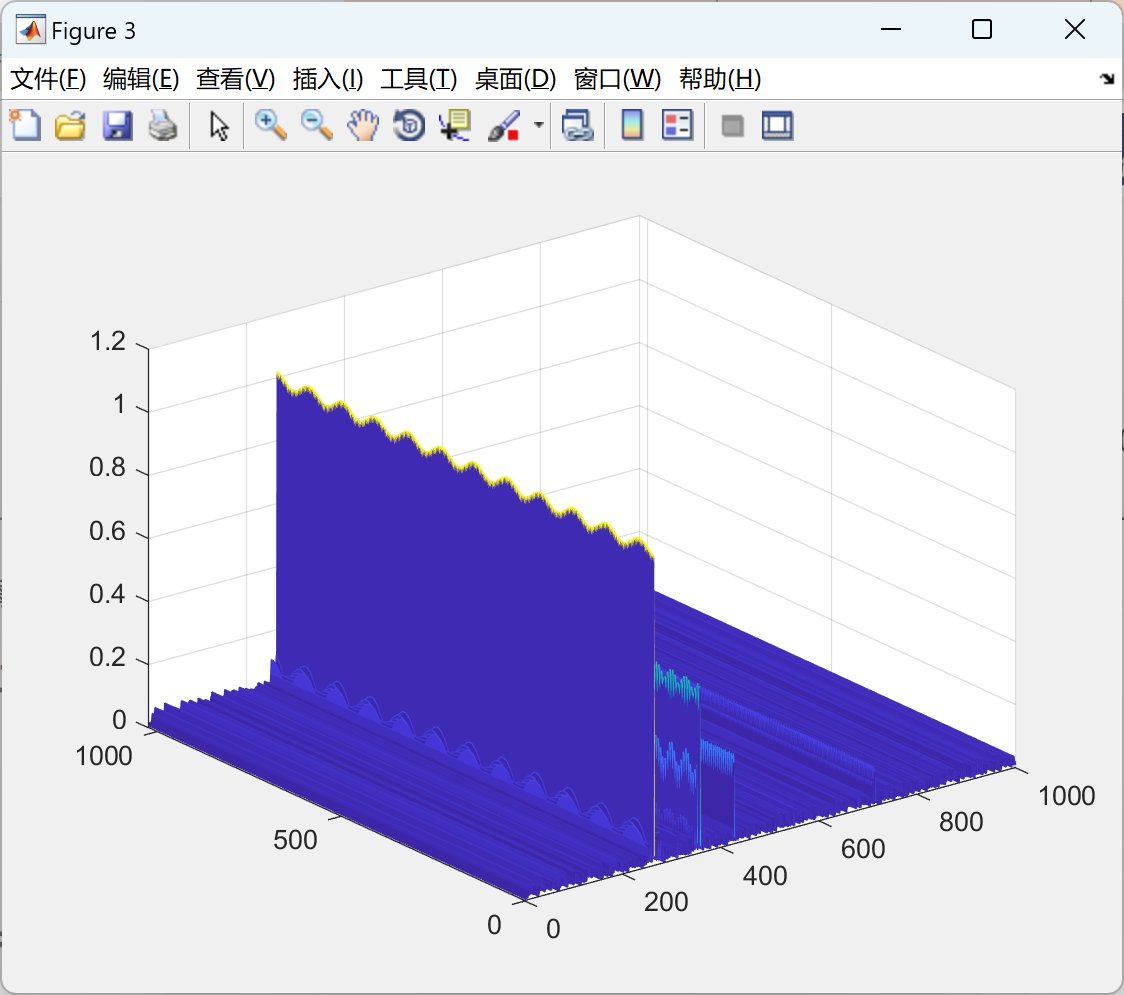
对1GHz脉冲多普勒雷达进行快速和慢速处理生成5个移动目标的距离多普勒图研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

uni.uploadFile上传 PHP接收不到
开始这样,后端$file $request->file(file);接收不到 数据跑到param中去了 去掉Content-Type,就能接收到了 param只剩下...

2023年高教社杯 国赛数学建模思路 - 复盘:光照强度计算的优化模型
文章目录 0 赛题思路1 问题要求2 假设约定3 符号约定4 建立模型5 模型求解6 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 问题要求 现在已知一个教室长为15米,宽为12米&…...
Netty简易聊天室
文章目录 本文目的参考说明环境说明maven依赖日志配置单元测试 功能介绍开发步骤 本文目的 通过一个简易的聊天室案例,讲述Netty的基本使用。同时分享案例代码。项目中用到了log4j2,junit5,同时分享这些基础组件的使用。项目中用到了awt&…...
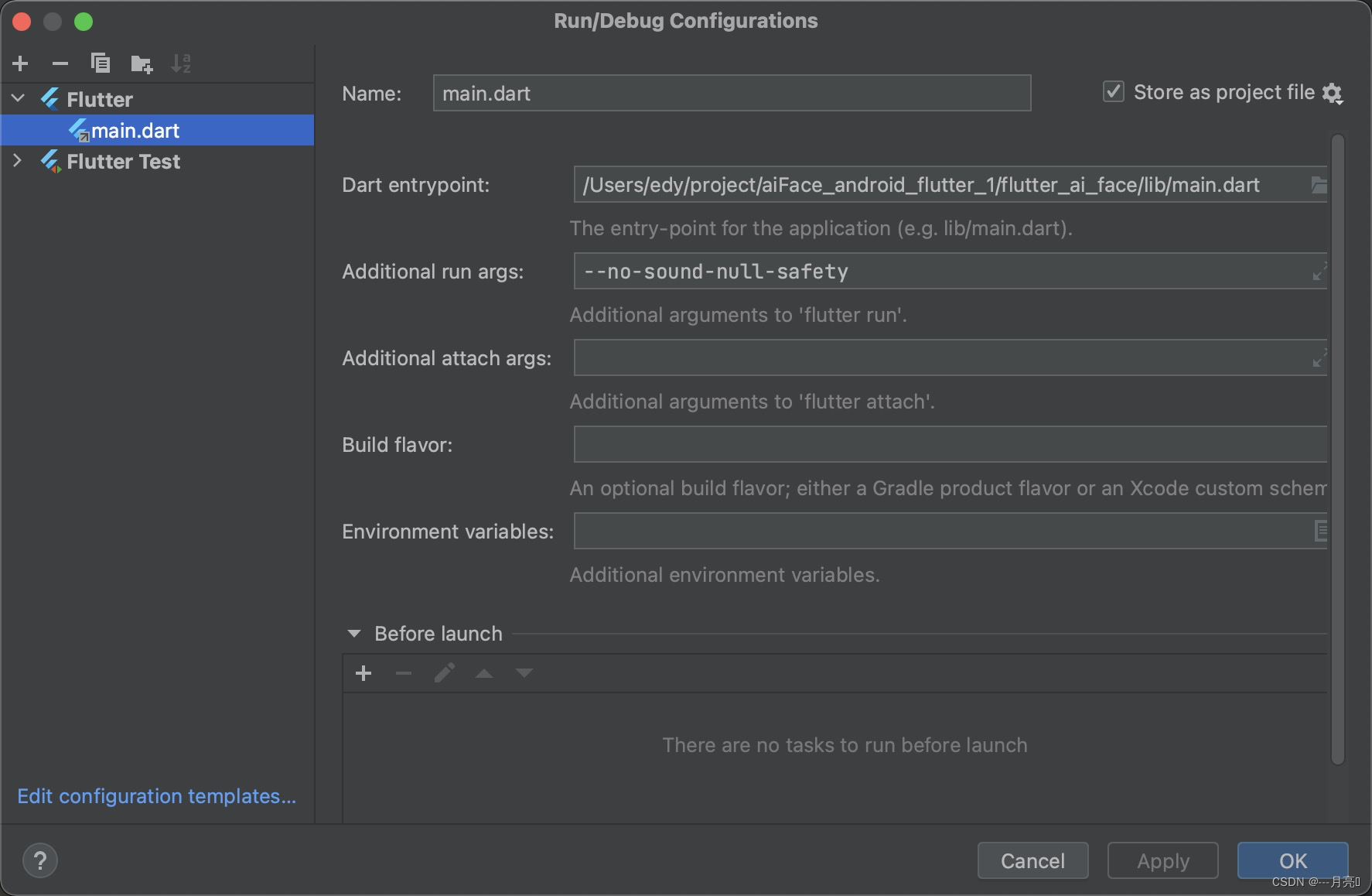
Flutter Cannot run with sound null safety, because the following dependencies
flutter sdk 版本升级到2.0或者更高的版本后,运行之前的代码会报错 Error: Cannot run with sound null safety, because the following dependencies dont support null safety:- package:flutter_swiper- package:flutter_page_indicator- package:transformer_p…...

利用改进的遗传算法(种群隔离与个体迁移)mpi并行解决tsp问题
序 关于tsp问题的概述以及如何使用遗传算法进行求解已经在上一篇文章中说明了:遗传算法解决TSP问题. 但是,作为一种演化算法,遗传算法还存在着许多问题,比如早熟的情况,很容易在算法前期就已经收敛了,大量…...

【C++】—— C++11之线程库
前言: 在本期,我将给大家介绍的是 C11 中新引进的知识,即关于线程库的相关知识。 目录 (一)线程库的介绍 1、线程库的由来 2、线程库的简单介绍 (二)线程函数参数 (三…...

前端面试:【性能优化】前端缓存、CDN、懒加载和预加载
亲爱的前端开发者,Web性能对用户体验至关重要。如果你想让你的网站更快、更具吸引力,就需要关注前端性能优化。在这篇文章中,我们将深入探讨四个关键的性能优化策略:前端缓存、CDN(内容分发网络)、懒加载和…...
民族传统文化分享系统uniapp 微信小程序
管理员、用户可通过Android系统手机打开系统,注册登录后可进行管理员后端;首页、个人中心、用户管理、知识分类管理、知识资源管理、用户分享管理、意见反馈、系统管理,用户前端;首页、知识资源、用户分享、我的等。 本系统的使用…...
:NIO——处理可写事件)
netty(二):NIO——处理可写事件
处理可写事件 什么情况下需要注册可写事件? 在服务端一次性无法把数据发送完的情况下,需要注册可写事件 服务端一次性是否能够把数据全部发送完成取决于服务端的缓冲区大小,该缓冲区不受程序控制 注册可写事件的步骤 判断ByteBuffer是否仍…...

PHP基本语法解析与应用指南
PHP(Hypertext Preprocessor)是一种广泛应用的开源脚本语言,特别适用于Web开发。本文将深入探讨PHP的基本语法,包括变量、数据类型、运算符、控制流等方面的内容。我们将详细介绍每个主题的基本概念、语法规则和常见应用ÿ…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
