当前位置： 首页 > news >正文

windows下安装go环境 和vscode中go扩展

news 2026/2/11 2:56:02

1. 首先安装GO

Go下载地址：go.dev

选择相对应的版本，下载，运行安装程序，并打开命令提示符，运行 go env ，确认已经安装go

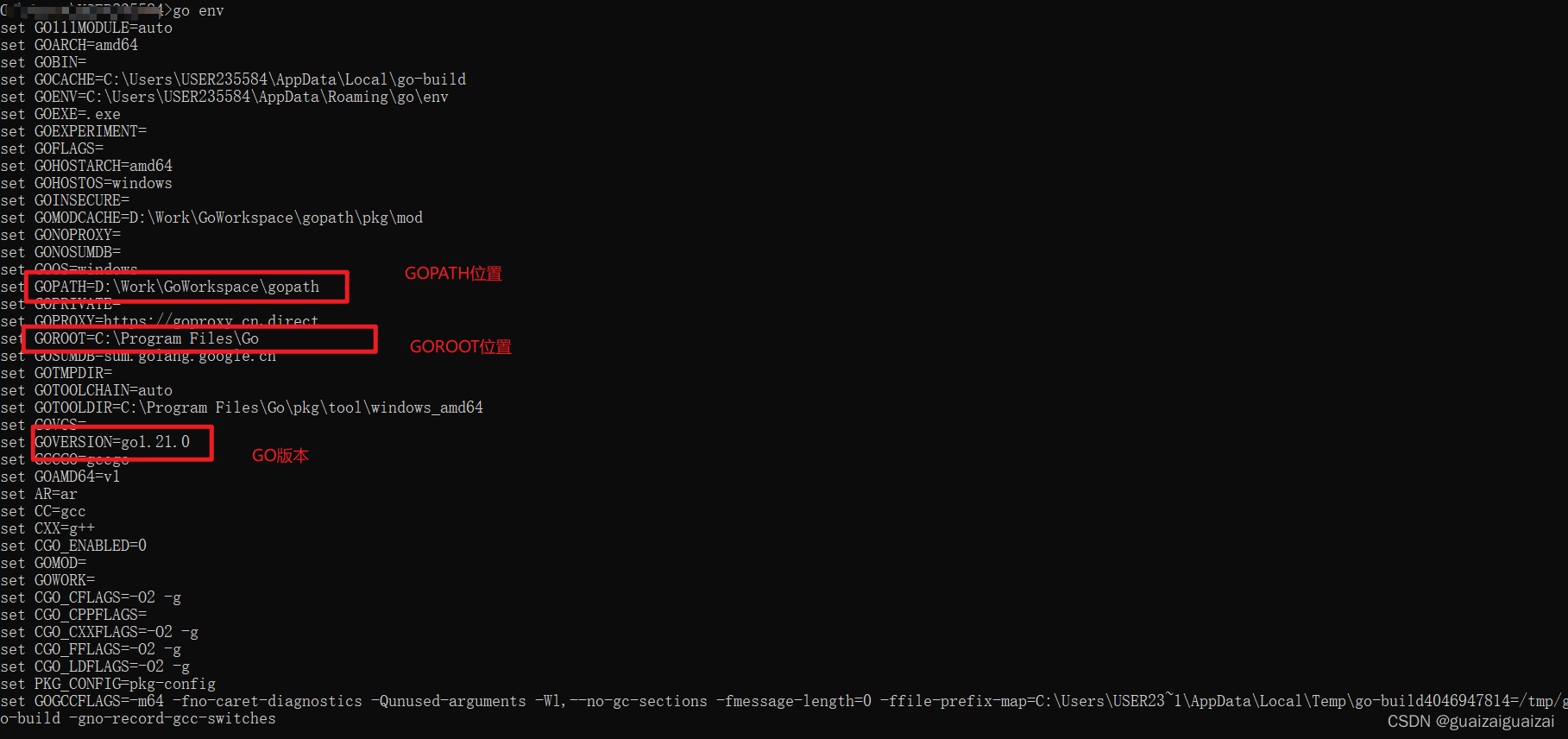
注意关注其中GOPATH和GOROOT，这两个地址可以在系统环境变量中进行设置。

在“设置”中找到“编辑系统环境变量”，之后点击“高级”，点击“环境变量”，在其中增加“GOPATH”和“GOROOT”两个变量.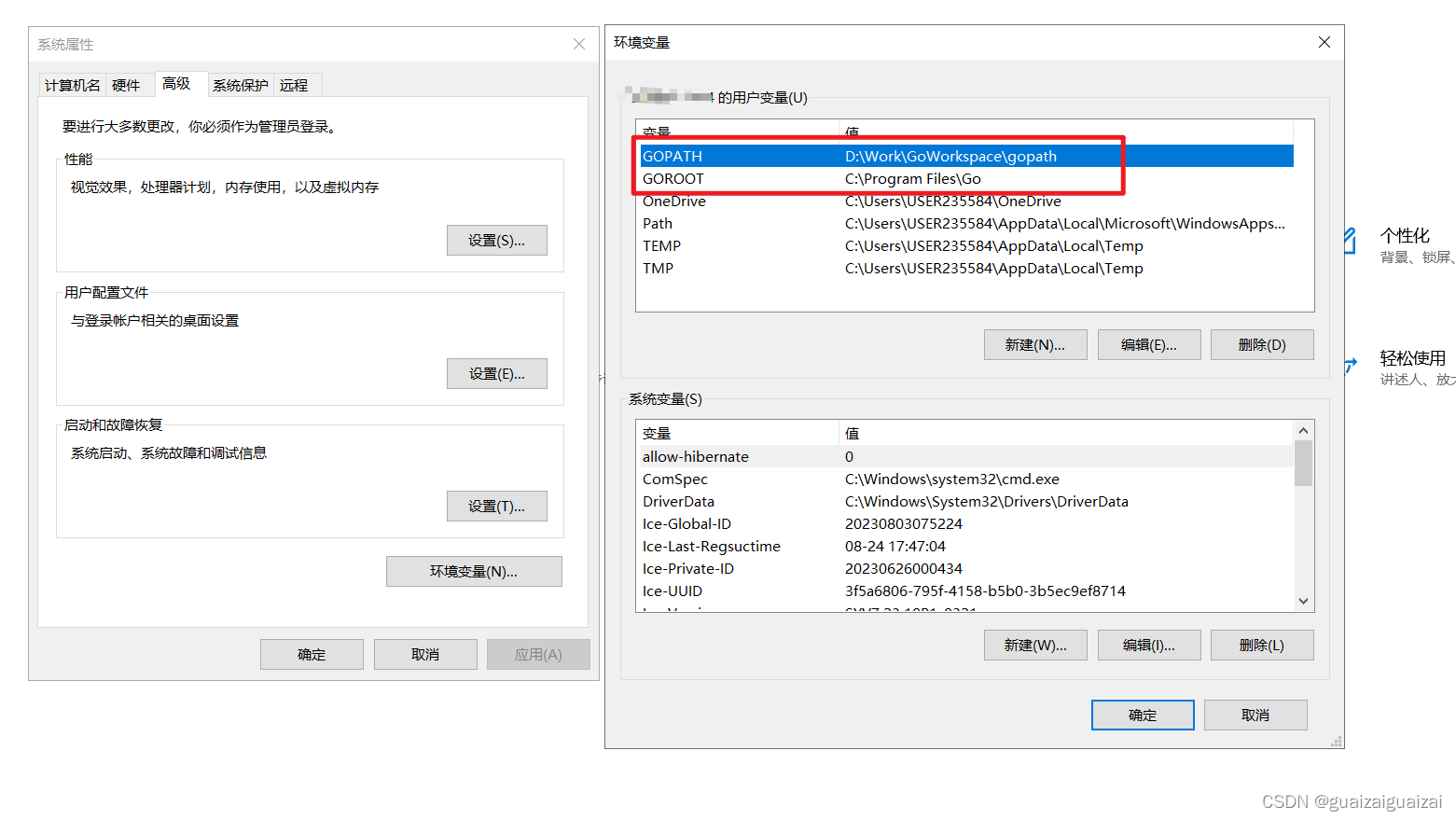

之后在“Path”变量中增加GOPATH和GOROOT，具体如下：

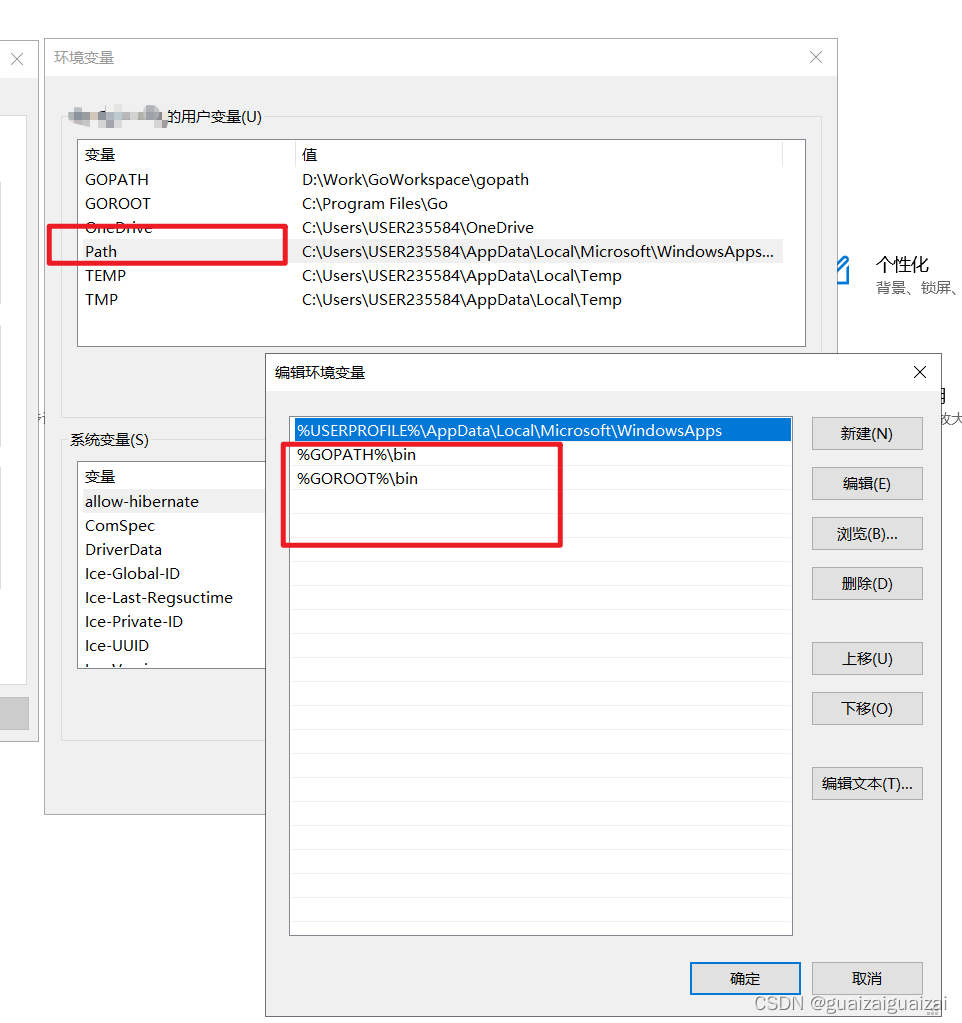
配置完成后在输入go env 查看是否设置成功。

2. 安装Visual Studio Code

下载地址：Visual Studio Code - Code Editing. Redefined

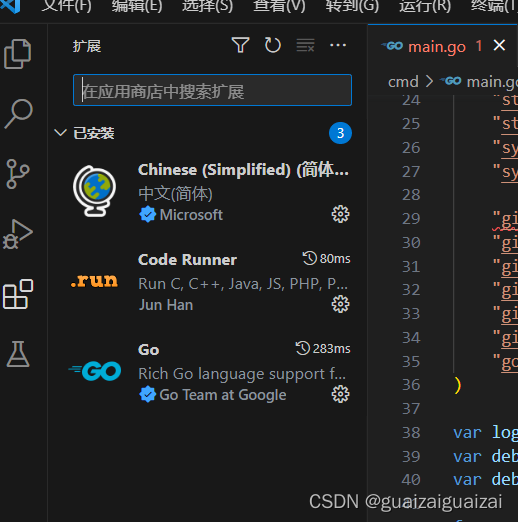
安装完成后，打开扩展，分别安装chinese、code runner、Go这三个扩展

3. 对Go扩展继续配置

打开G扩展的扩展设置

 

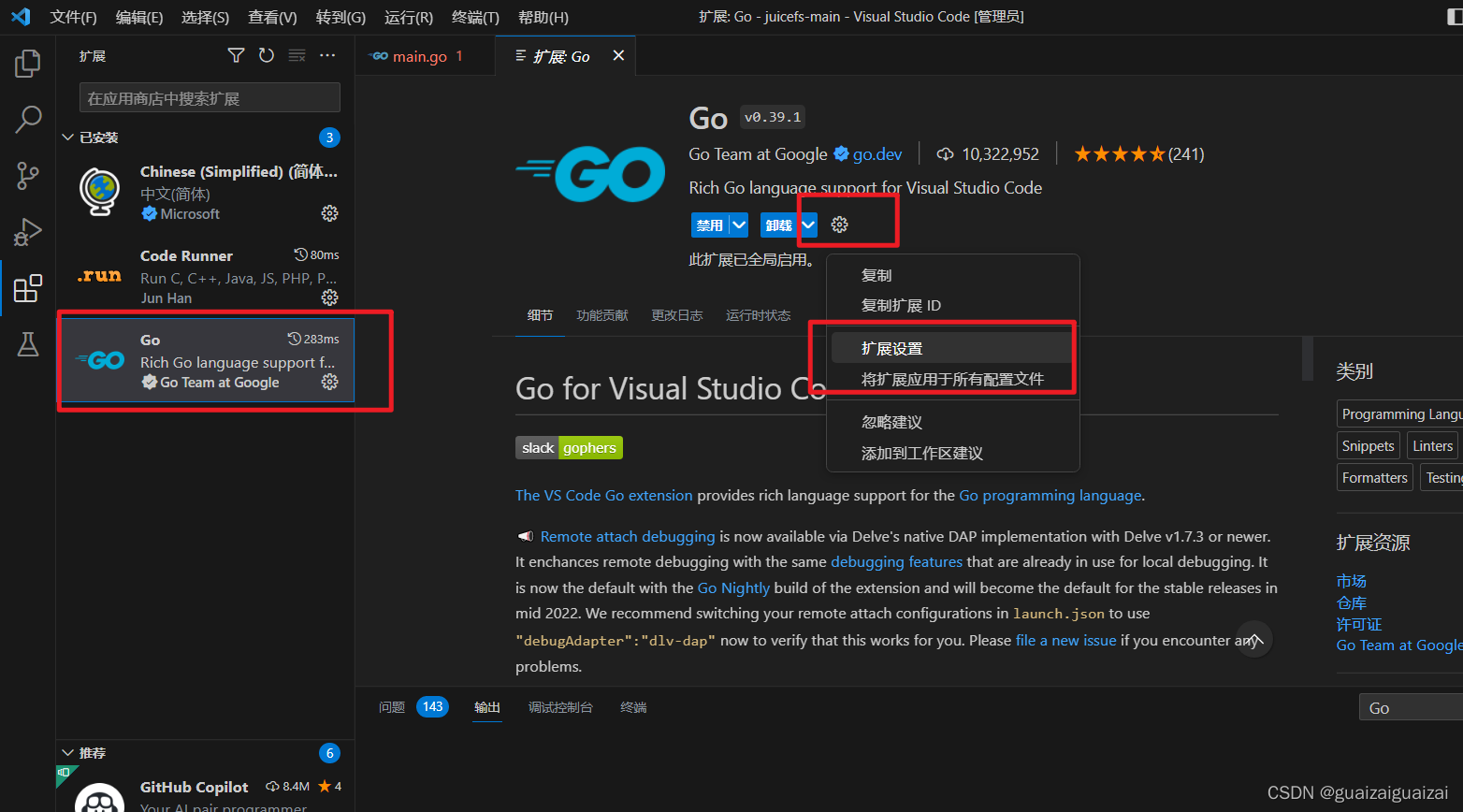
在其中找到Gopath，点击 在settings.json中编辑

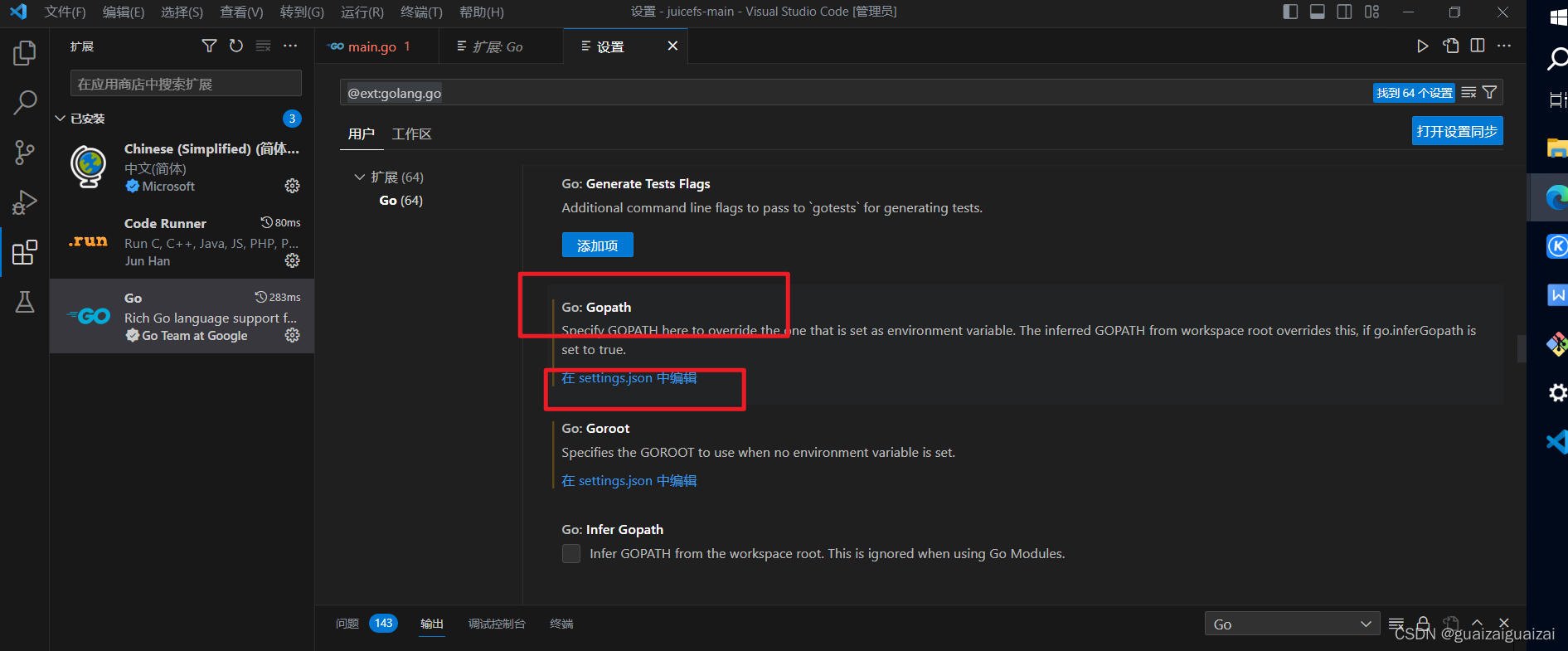
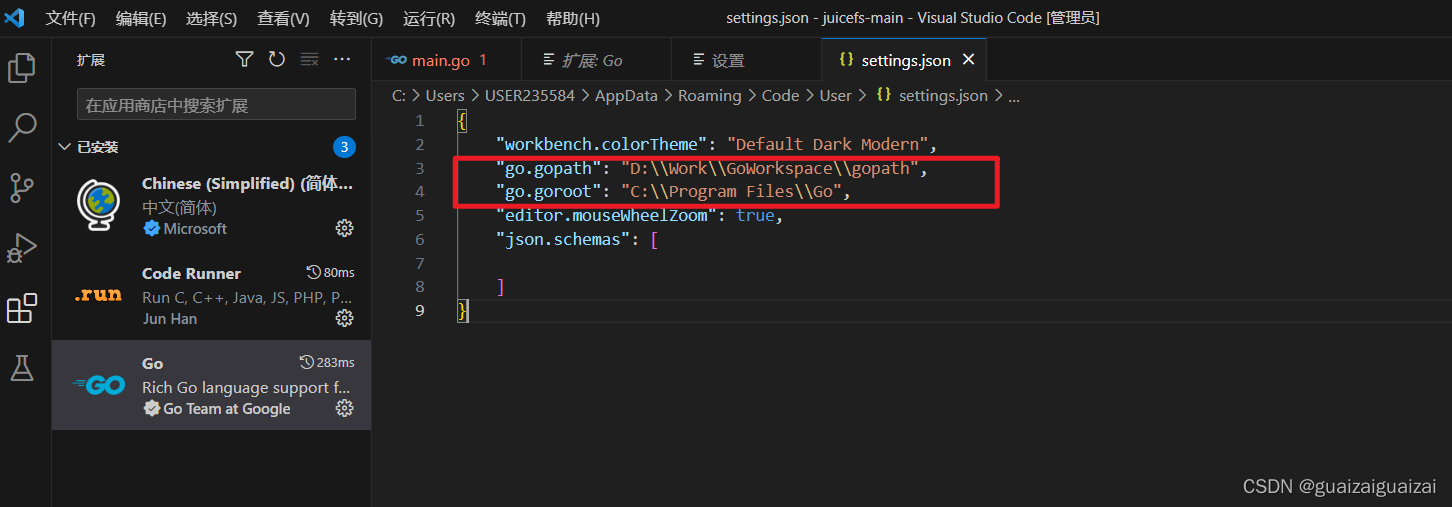
将自己设置的GOPATH和GOROOT写入即可

参考：

为 Go 开发配置Visual Studio Code - Go on Azure | Microsoft Learn

 

 

 

相关文章：

windows下安装go环境 和vscode中go扩展

1. 首先安装GO Go下载地址：go.dev 选择相对应的版本，下载，运行安装程序，并打开命令提示符，运行 go env ，确认已经安装go 注意关注其中GOPATH和GOROOT，这两个地址可以在系统环境变量中进行设置…...

编程日记 2023/8/28 16:43:01

C++ 面试题（一）--C++基础，面向对象，内存管理

目录 1.part1 C基础 1 C特点 2 说说C语言和C的区别 3 说说 C中 struct 和 class 的区别 4 include头文件的顺序以及双引号""和尖括号<>的区别 5 说说C结构体和C结构体的区别 6 导入C函数的关键字是什么&#xff0c;C编译时和C有什么不同&#xff1f; 7…...

编程日记 2023/8/28 16:42:00

ARTS打卡第二周之链表环的检测、gdb中disassemble的使用、底层学习建议、学习分享

Algorithm 题目&#xff1a;链表中环的检测 自己的分析见博客《检测链表中是否存在环》 Review disassemble command是我读的一篇英语文章&#xff0c;这篇文章主要是介绍gdb反汇编命令的使用和参数。自己为了能够演示这篇文章里边的内容&#xff0c;特意自己使用汇编语言编…...

编程日记 2023/8/28 16:40:59

皕杰报表(BIOS Report)中设置序号的方法之二

在皕杰报表如何设置序号系列之一里&#xff0c;我们用ds.#0来实现了序号&#xff0c;用ds.#0得到的数据库中选取的记录的序号。有些情况下&#xff0c;记录序号在报表中不是按照顺序显示的&#xff0c;而是在报表中又通过排序或分组后的结果显示的&#xff0c;例如&#xff1a;…...

编程日记 2023/8/28 16:39:56

nacos总结黑马

SpringCloud实用篇02 0.学习目标 1.Nacos配置管理 Nacos除了可以做注册中心&#xff0c;同样可以做配置管理来使用。 1.1.统一配置管理 当微服务部署的实例越来越多&#xff0c;达到数十、数百时&#xff0c;逐个修改微服务配置就会让人抓狂&#xff0c;而且很容易出错。我…...

编程日记 2023/8/28 16:38:55

【简单bat】写一个定时关机的批处理程序

感谢我那可爱的GPT助手对代码的优化工作。 echo off REM Author: liyang TEL 155-4089-9552echo 欢迎使用自动关机计划设置脚本&#xff01;by LiYang echo.:choose_action set /p "action_choice请选择要执行的操作&#xff08;输入1设置定时关机任务&#xff0c;输入2删…...

编程日记 2023/8/28 16:37:54

Oracle 19c 启动和关闭实例保存PDB状态

简介&#xff1a; 十年以上 MySQL Oracle DBA从业者&#xff0c;MySQL 5.7 OCP&#xff0c; 微信号: jinjushuke 当前有一个PDB 打开模式为READ WRITE [oracleDGMOGGM19C ~]$ sql sys192.168.3.107:1521/pdb1 as sysdba SQLcl: Release 19.1 Production on Wed Aug 23 10:19:…...

编程日记 2023/8/28 16:36:52

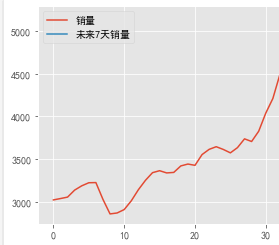
计算机毕设 基于机器学习的餐厅销量预测 -大数据 python

文章目录 0 前言餐厅销量预测模型简介2.ARIMA模型介绍2.1自回归模型AR2.2移动平均模型MA2.3自回归移动平均模型ARMA 三、模型识别四、模型检验4.1半稳性检验(1)用途(1)什么是平稳序列?(2)检验平稳性 ◆白噪声检验(纯随机性检验)(1)用途(1)什么是纯随机序列?(2)检验纯随机性 五…...

编程日记 2023/8/28 16:35:51

layui 多选限制选择3个

可以使用 layui 的表单组件进行多选&#xff0c;然后通过 JavaScript 代码限制用户最多只能选择 3 个选项。具体的实现步骤如下&#xff1a; 在 layui 的表单组件中&#xff0c;使用多选框进行多选。 <div class"layui-form-item"><label class"layu…...

编程日记 2023/8/28 16:34:49

PyQt PySide6 QMessageBox使用教程

PySide6 是一个 Python 绑定到 Qt6 库的库&#xff0c;允许你在 Python 中创建 Qt6 应用程序。QMessageBox 是一个提供模式对话框&#xff0c;用于显示消息、询问问题或获取简单的输入的类。 以下是使用 PySide6 中的 QMessageBox 的基本方式&#xff1a; 导入必要的模块: f…...

编程日记 2023/8/28 16:33:48

Visual Studio软件安装包分享（附安装教程）

目录 一、软件简介 二、软件下载 一、软件简介 Visual Studio是微软公司开发的一款集成开发环境&#xff08;IDE&#xff09;&#xff0c;广泛应用于Windows平台上的应用程序和Web应用程序的开发。以下是Visual Studio软件的主要特点和功能&#xff1a; 集成开发环境&#x…...

编程日记 2023/8/28 16:32:44

VB电脑销售系统设计与实现

前 言 本文论述了销售管理系统的开发过程，它包括了软件的开发环境，开发工具以及相关技术、系统分析、系统设计、实现等内容。 本系统能为企业繁重的工作带来极大的方便，提高了工作效率及工作准确性，能准确无误地查找货物的综合信息，为企业减少了许多工作细节。 为了使此…...

编程日记 2023/8/28 16:31:43

如何访问MySQL错误日志

通常情况下&#xff0c;MySQL中出现减速、崩溃或其他意外行为的根本原因可以通过分析错误日志来确定。在Ubuntu系统中&#xff0c;MySQL的默认位置是/var/log/mysql/error.log。在许多情况下&#xff0c;使用less程序最容易读取错误日志&#xff0c;这是一个命令行实用程序&…...

编程日记 2023/8/28 16:30:41

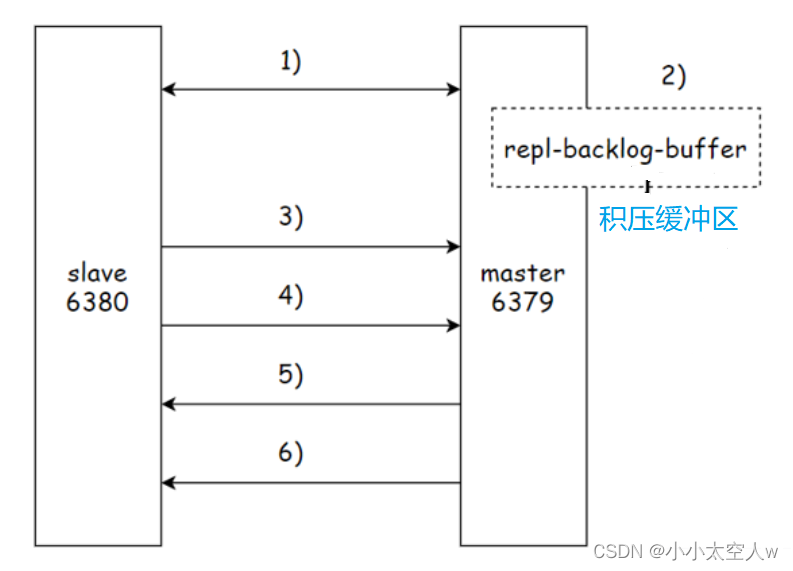
redis主从复制详解

目录 前言&#xff1a; 分布式系统 主从模式 主从同步连接过程 replication id作用 offset作用 psync命令&#xff08;psync replicationId offset) 全量复制 全量复制过程 部分复制 部分复制过程 实时复制 前言&#xff1a; redis为了保证高可用&#xff0c;它支持…...

编程日记 2023/8/28 16:29:40

kubernetes/k8s驱逐机制总结篇

概述 k8s的驱逐机制是指在某些场景下&#xff0c;如node节点notReady、node节点压力较大等&#xff0c;将pod从某个node节点驱逐掉&#xff0c;让pod的上层控制器重新创建出新的pod来重新调度到其他node节点。这里也将kube-scheduler的抢占调度纳入到了驱逐的讨论范围内&#…...

编程日记 2023/8/28 16:28:39

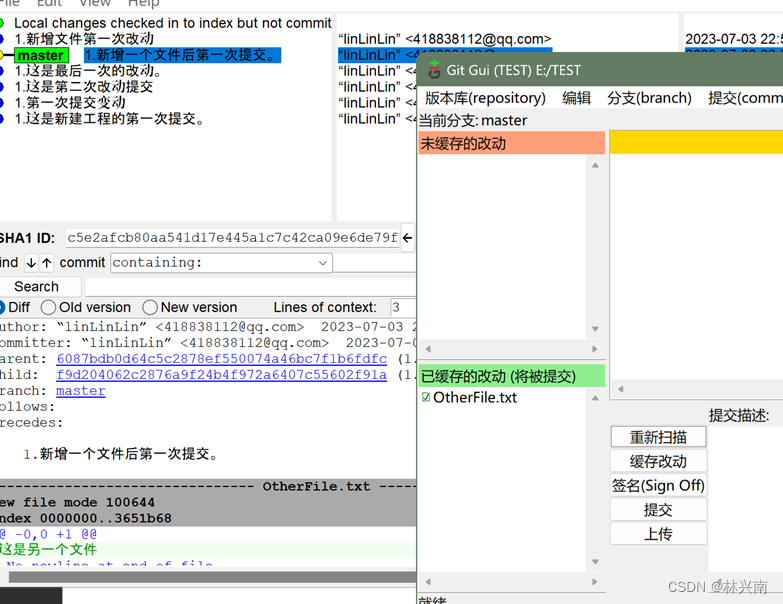
Git gui教程---第七篇 Git gui的使用 返回上一次提交

1&#xff0e; 查看历史&#xff0c;打开gitk程序 2&#xff0e; 选中需要返回的版本&#xff0c;右键&#xff0c;然后点击Rest master branch to here 3.出现弹窗 每个选项我们都试一下&#xff0c;从Hard开始 返回的选项 HardMixedSoft Hard 会丢失所有的修改【此处的…...

编程日记 2023/8/28 16:27:38

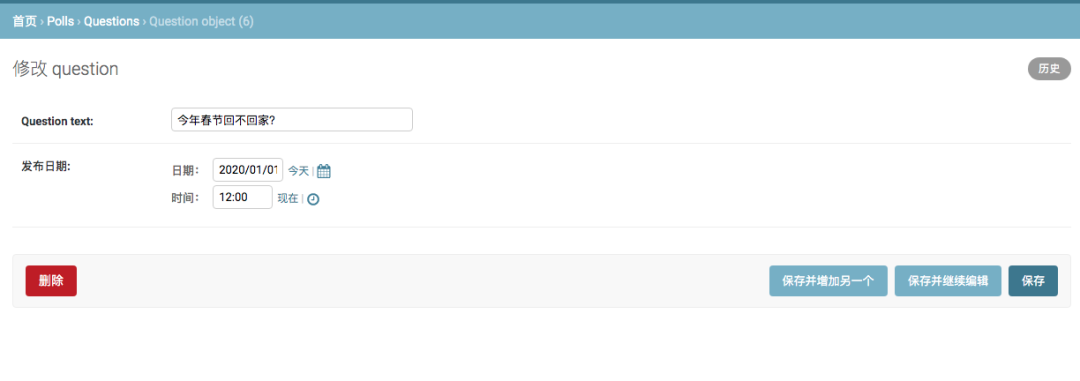
Web 开发 Django 管理工具

上次为大家介绍了 Django 的模型&#xff0c;通过模型就可以操作数据库&#xff0c;从而就可以改变页面的展示内容&#xff0c;那问题来了&#xff0c;我们只能通过手动编辑模型文件来配置模型吗&#xff1f;当然不是&#xff0c;Django 为我们提供了强大的工具&#xff0c;可以…...

编程日记 2023/8/28 16:26:34

分类算法的评价指标

分类算法的评价指标 查准率、查全率、准确率、F1分数&#xff1a; 查准率&#xff08;Precision&#xff09;&#xff1a; 模型预测为正例的样本中实际未正的比例。它关注的点在&#xff1a;预测为正例样本的准确性。 查全率&#xff08;recall&#xff09;&#xff1a; 模型…...

编程日记 2023/8/28 16:25:33

智能工厂移动式作业轻薄加固三防平板数据采集终端

在这个高度自动化和数字化的环境中&#xff0c;数据采集变得尤为重要。为了满足这个需求&#xff0c;工业三防平板数据采集终端应运而生。工业三防平板数据采集终端采用了轻量级高强度镁合金材质&#xff0c;这使得它在保持轻薄的同时具有更强的坚固性。这种材质还具有耐磨防损…...

编程日记 2023/8/28 16:24:31

Python Flask token身份认证

首先安装依赖&#xff1a; pip install flask-jwt-extended 然后在主应用中&#xff08;项目入口文件&#xff09;加入以下代码&#xff1a; from flask import Flask from flask_jwt_extended import JWTManager #引入依赖 app Flask(__name__) app.config[JWT_SECRET_KEY…...

编程日记 2023/8/28 16:23:29

CTF show Web 红包题第六弹

提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框&#xff0c;很难让人不联想到SQL注入&#xff0c;但提示都说了不是SQL注入&#xff0c;所以就不往这方面想了 ​ 先查看一下网页源码&#xff0c;发现一段JavaScript代码&#xff0c;有一个关键类ctfs…...

编程新知 2026/2/5 4:33:58

＜6＞-MySQL表的增删查改

目录 一&#xff0c;create&#xff08;创建表&#xff09; 二&#xff0c;retrieve&#xff08;查询表&#xff09; 1&#xff0c;select列 2&#xff0c;where条件 三&#xff0c;update&#xff08;更新表&#xff09; 四&#xff0c;delete&#xff08;删除表&#xf…...

编程新知 2025/12/11 18:28:17

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法

树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源&#xff1a; http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作&#xff0c;无需更改相机配置。但是&#xff0c;一…...

编程新知 2026/2/5 4:39:03

Appium+python自动化（十六）- ADB命令

简介 Android 调试桥(adb)是多种用途的工具&#xff0c;该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具&#xff0c;其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利&#xff0c;如安装和调试…...

编程新知 2026/1/21 18:20:51

Python：操作 Excel 折叠

💖亲爱的技术爱好者们，热烈欢迎来到 Kant2048 的博客！我是 Thomas Kant，很开心能在CSDN上与你们相遇～💖 本博客的精华专栏： 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

编程新知 2026/2/10 13:23:50

UE5 学习系列（三）创建和移动物体

这篇博客是该系列的第三篇&#xff0c;是在之前两篇博客的基础上展开&#xff0c;主要介绍如何在操作界面中创建和拖动物体&#xff0c;这篇博客跟随的视频链接如下&#xff1a; B 站视频&#xff1a;s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

编程新知 2026/1/24 10:00:31

Python爬虫（一）：爬虫伪装

一、网站防爬机制概述 在当今互联网环境中&#xff0c;具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类&#xff1a; 身份验证机制&#xff1a;直接将未经授权的爬虫阻挡在外反爬技术体系&#xff1a;通过各种技术手段增加爬虫获取数据的难度…...

编程新知 2026/1/30 20:42:46

大学生职业发展与就业创业指导教学评价

这里是引用 作为软工2203/2204班的学生&#xff0c;我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要&#xff0c;而您认真负责的教学态度&#xff0c;让课程的每一部分都充满了实用价值。 尤其让我…...

编程新知 2025/11/16 1:39:27

JVM 内存结构 详解

内存结构 运行时数据区&#xff1a; Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器&#xff1a; ​ 线程私有&#xff0c;程序控制流的指示器&#xff0c;分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 ​ 每个线程都有一个程序计数…...

编程新知 2026/2/6 3:24:58

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制

使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下&#xff0c;限制某个 IP 的访问频率是非常重要的&#xff0c;可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案&#xff0c;使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

编程新知 2025/10/22 6:06:44