【图论】拓扑排序
一.定义
![]()
拓扑排序是一种对有向无环图(DAG)进行排序的算法,使得图中的每个顶点在排序中都位于其依赖的顶点之后。它通常用于表示一些任务之间的依赖关系,例如在一个项目中,某些任务必须在其他任务之前完成。
拓扑排序的步骤如下:
-
找到入度为0的顶点:入度是指指向某个顶点的边的数量。首先,找到图中入度为0的顶点,它们是没有依赖关系的顶点,可以作为排序的起点。
-
将入度为0的顶点移出图:选择一个入度为0的顶点,将其从图中移除,并将与之相邻的顶点的入度减1。
-
重复步骤1和步骤2:重复上述步骤,直到所有顶点都被移除。如果图是有向无环图,那么拓扑排序会成功完成。
拓扑排序并不是对所有图都适用,只有在有向无环图中才有意义,因为循环依赖会导致拓扑排序无法进行。
二.例题
B3644 【模板】拓扑排序 / 家谱树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
三.思路
找出入度为0的点,即为最小辈分的,输出即可,然后取消它的所有连边。
eg:
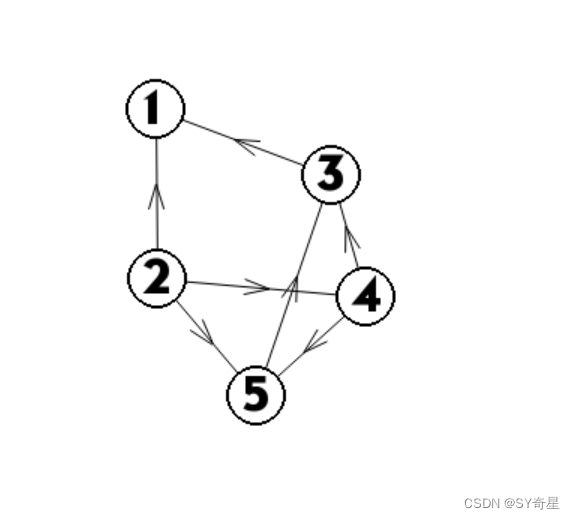
可知2无入度,说明2的辈分最小,输出并删除它的连边,print(2)

这时4无入度,print(2,4)
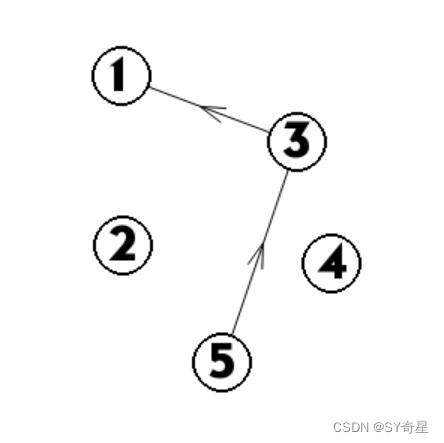
一直重复,print(2,4,5,3,1)
四.参考代码
#include<bits/stdc++.h>
using namespace std;
vector<int>to[101];
int in[101];
queue<int>q;
int main(){int n;scanf("%d",&n);for(int i=1;i<=n;i++){int x;while(scanf("%d",&x) && x!=0){to[i].push_back(x);in[x]++;}}for(int i=1;i<=n;i++){if(!in[i]) q.push(i);}while(!q.empty()){int x=q.front();q.pop();cout<<x<<" ";for(int i=0;i<to[x].size();i++){int y=to[x][i];in[y]--;if(!in[y]) q.push(y);}}return 0;
}
五.拓扑+dp
P1807 最长路 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
六.思路
不就是最长路吗?Dijkstra直接秒杀。
但还有什么更快的算法吗?
注意:这是有向无环图(DAG),是不是拓扑排序更快呢?拓扑排序就可以找到图的所有直径,然后DP即可。最后输出dp[n];
状态转移方程为:dp[v]=max(dp[v],dp[u]+w);
若dp[n]<0,那就说明没有边可以到达n点
七.参考代码
#include<bits/stdc++.h>
#define maxn 1505
using namespace std;
int n,m;
vector<int> to[maxn],wt[maxn];
int in[maxn],dp[maxn];
queue<int> q;
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){int u,v,w;scanf("%d%d%d",&u,&v,&w);to[u].push_back(v);wt[u].push_back(w);in[v]++; }for(int i=1;i<=n;i++){dp[i]=-1e9;if(in[i]==0) q.push(i) ;}dp[1]=0;while(!q.empty()){int x=q.front(); q.pop();for(int i=0;i<to[x].size();i++){int y=to[x][i],w=wt[x][i];dp[y]=max(dp[y],dp[x]+w);in[y]--;if(!in[y]) q.push(y);}}if(dp[n]<0) cout<<-1;else cout<<dp[n];return 0;
}
相关文章:

【图论】拓扑排序
一.定义 拓扑排序是一种对有向无环图(DAG)进行排序的算法,使得图中的每个顶点在排序中都位于其依赖的顶点之后。它通常用于表示一些任务之间的依赖关系,例如在一个项目中,某些任务必须在其他任务之前完成。 拓扑排序的…...
自动化备份方案
背景说明 网上有很多教程,写的都是从零搭建一个什么什么,基本上都是从无到有的教程,但是,很少有文章提及搭建好之后如何备份,这次通过请教GitHub Copilot Chat,生成几个备份脚本,以备后用。 注…...
win11出现安全中心空白和IT管理员已限制对此应用的某些区域的访问
问题 windows安全中心服务被禁用 winr 输入services.msc 找到windows安全中心服务查看是否被禁用,改为启动,不可以改动看第三条 打开设置,找到应用—windows安全中心–终止–修复–重置 重启如果还是不行看第四条 家庭版系统需要打开gped…...

github实用指令(实验室打工人入门必备)
博主进入实验室啦,作为一只手残党决定在这里分享一些常用的github使用情景和操作指南来解救其他手残党。 内容随着情景增加实时更新。如果只有没几个内容说明场景不多(相信对手残党而言是再好不过的消息) 情景一:…...
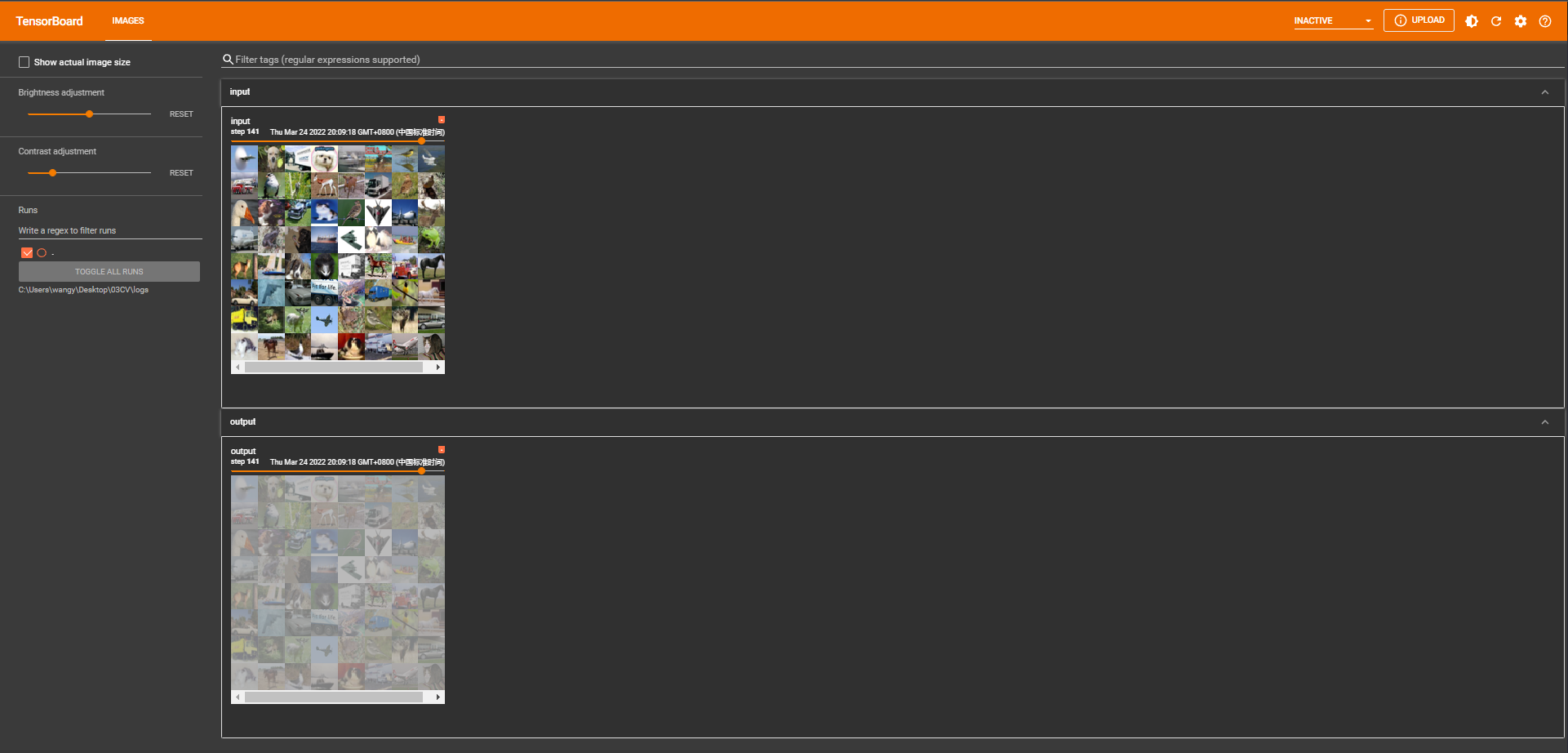
6. 激活层
6.1 非线性激活 ① inplace为原地替换,若为True,则变量的值被替换。若为False,则会创建一个新变量,将函数处理后的值赋值给新变量,原始变量的值没有修改。 import torch from torch import nn from torch.nn import …...
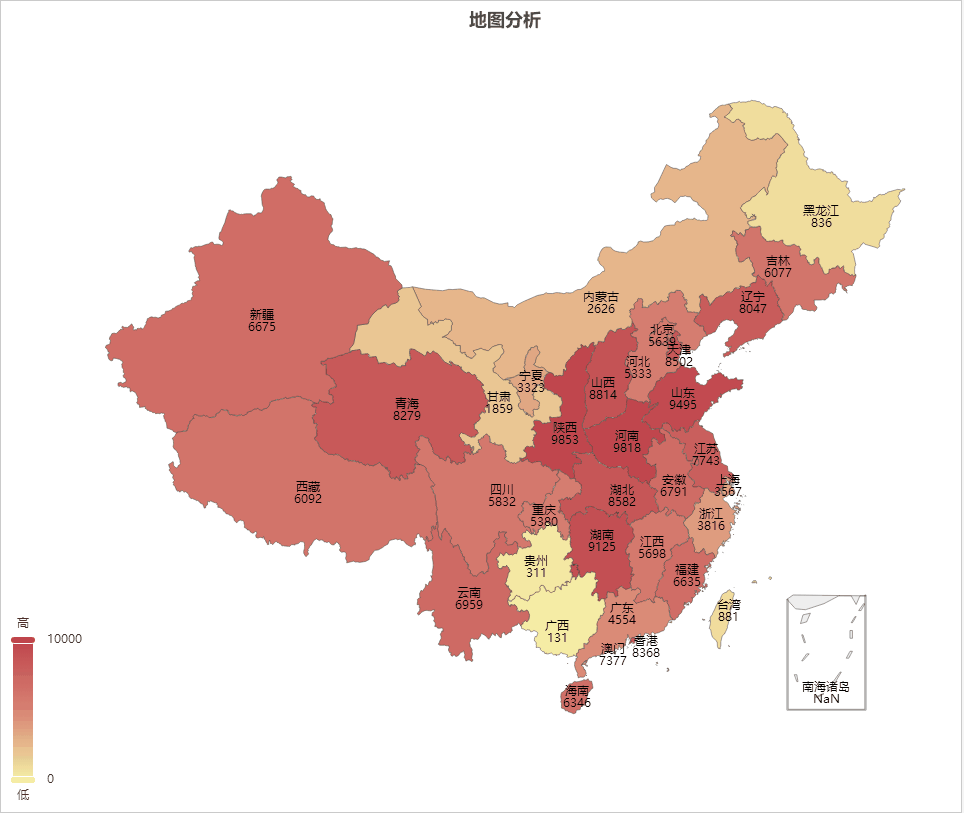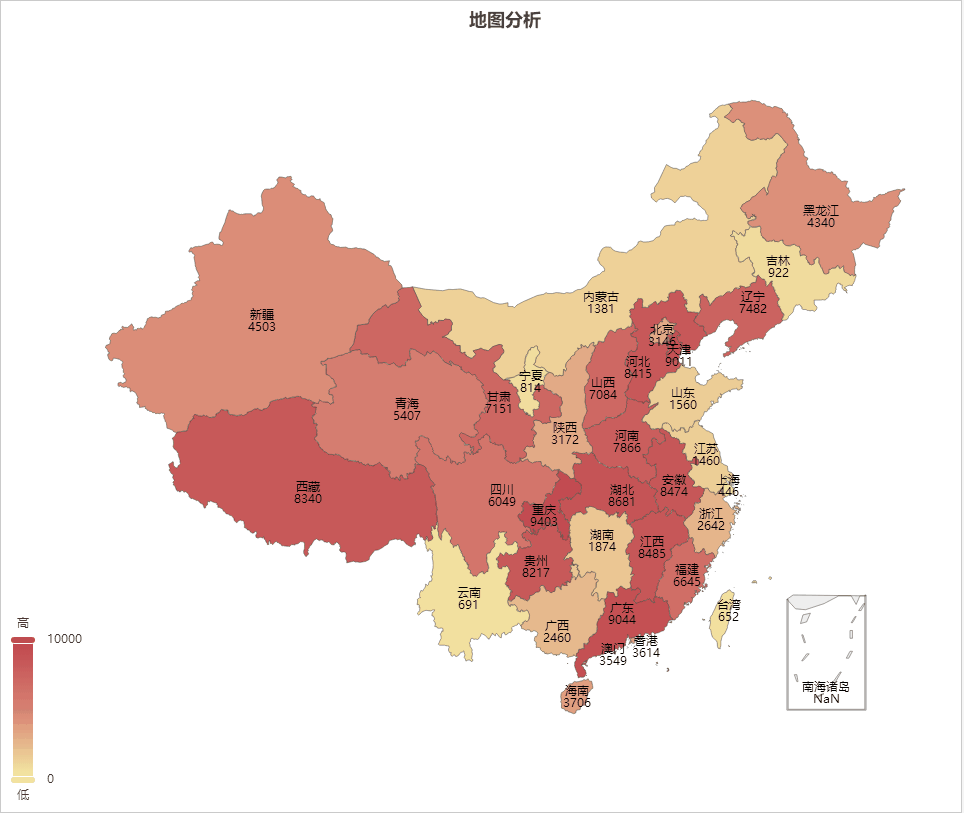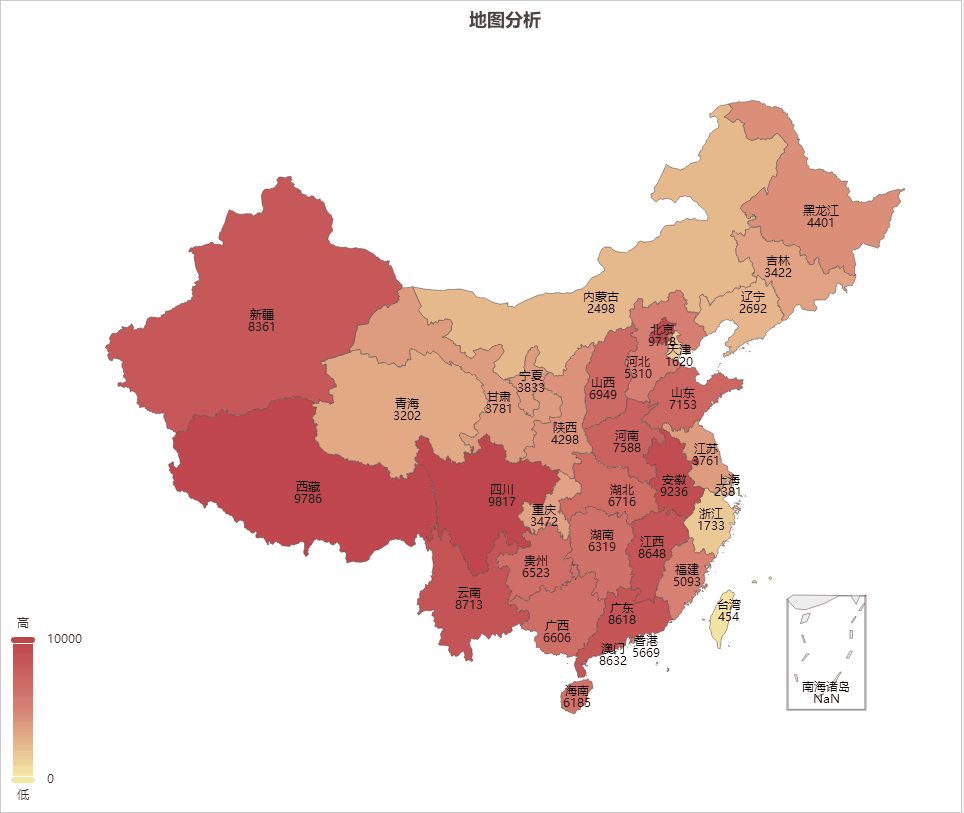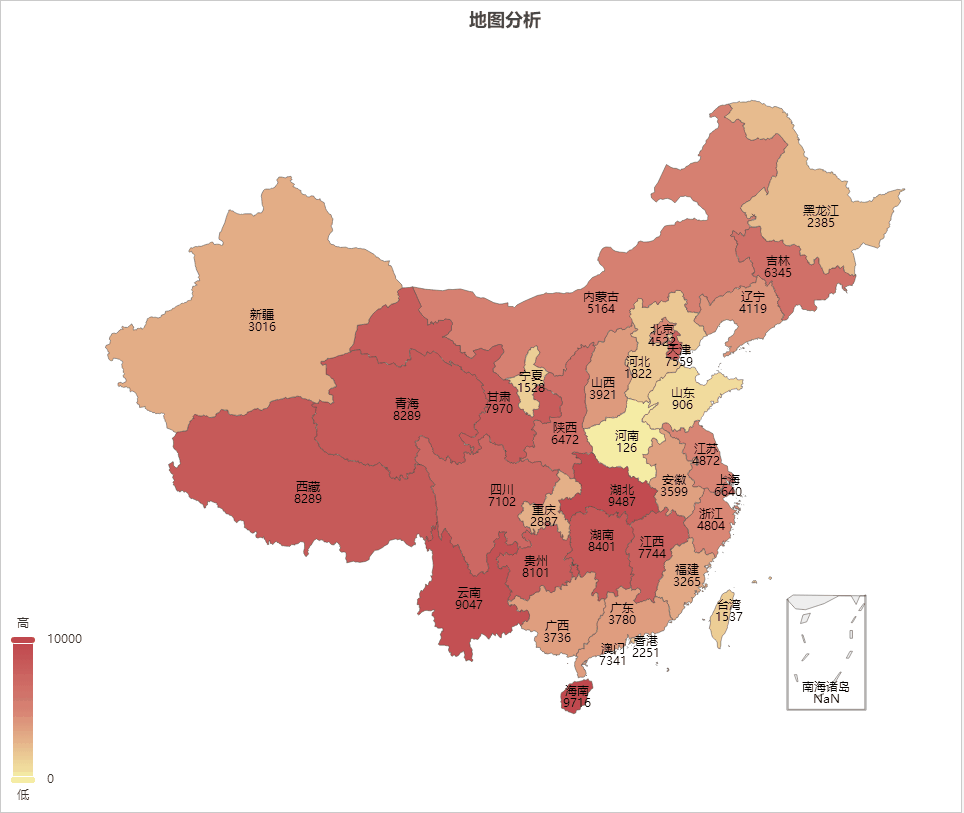
AIGC ChatGPT 制作地图可视化分析
地图可视化分析是一种将数据通过地图的形式进行展示的方法,可以让人们更加直观、快速、准确的理解和分析数据。以下是地图可视化分析的一些主要好处: 加强数据理解:地图可视化可以将抽象的数字转化为直观的图形,帮助我们更好地理解复杂的数据集。 揭示地理模式:地理位置是…...
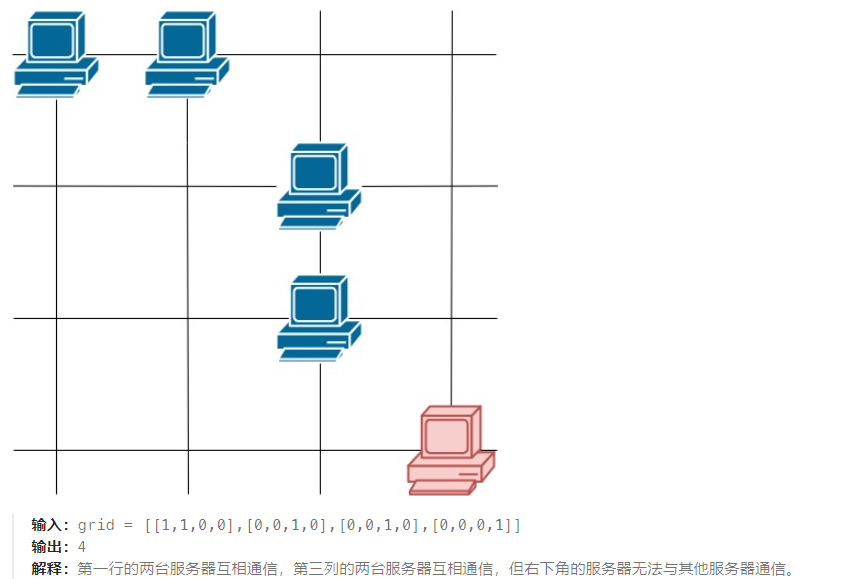
2023-08-24 LeetCode每日一题(统计参与通信的服务器)
2023-08-24每日一题 一、题目编号 1267. 统计参与通信的服务器二、题目链接 点击跳转到题目位置 三、题目描述 这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有。 如果两台…...

前端实习day35
今天是下早班的一天,下完班直接赶车回广州了,吐槽一下深圳站管理得真得差,候车厅小,人巨多,而且进站口的标识也很少,绕了好久才找到!下次再也不去了。 今天是改bug的一天,但是有半天…...

Linux安装jupyter notebook
1. Linux安装jupyter notebook 1.1 生成配置文件 这里在conda环境中安装。 jupyter notebook --generate-config --allow-root上面命令是生成配置文件,并且允许使用root用户运行。配置文件默认生成到~/.jupyter/jupyter_notebook_config.py。 具体解释如下&…...

【猿灰灰赠书活动 - 03期】- 【RHCSA/RHCE 红帽Linux认证学习指南(第7版) EX200 EX300】
说明:博文为大家争取福利,与清华大学出版社合作进行送书活动 图书:《RHCSA/RHCE 红帽Linux认证学习指南(第7版) EX200 & EX300》 一、好书推荐 图书介绍 《RHCSA/RHCE 红帽Linux认证学习指南(第7版) EX200 & E…...

当 Tubi 遇到 Ruby
有人说 Tubi 作为 RubyConf China 金牌赞助商,明明用极具吸引力的 Elixir 后端工程师岗位和高品质的 Elixir Meetup,“拐走了”一批又一批 Rubyist 投身于 Elixir 开发中,却依然让人想在 Tubi 展台前多停留一会儿。 为什么工程师、校友甚至 …...
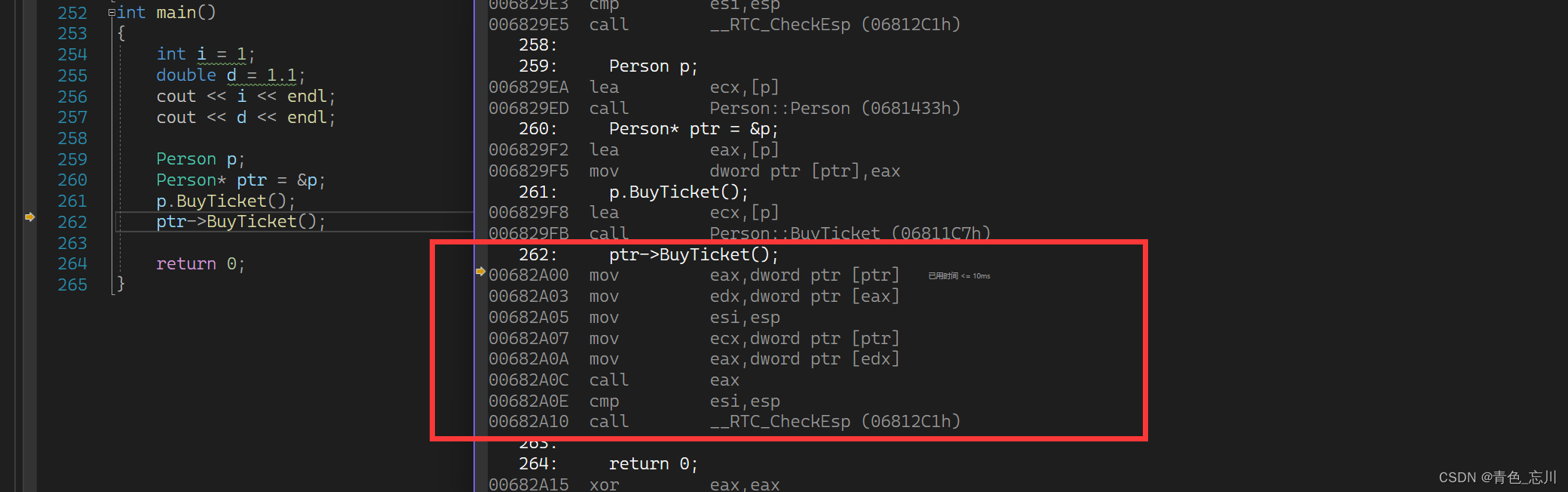
【C++从0到王者】第二十四站:多态的底层原理
文章目录 前言一、虚函数表二、一道经典的例题三、深度剖析多态的条件之一:为什么必须是父类的指针或引用四、深度剖析多态的条件之二:为什么是虚函数的重写/覆盖?五、虚函数表的一些总结六、关于Func3的验证七、动态绑定与静态绑定八、总结 …...

Java从入门到精通24==》数据库、SQL基本语句、DDL语句
Java从入门到精通24》数据库、SQL基本语句、DDL语句 2023.8.27 文章目录 <center>Java从入门到精通24》数据库、SQL基本语句、DDL语句一、什么是数据库二、数据库的优缺点1、使用数据库的优点:2、使用数据库的缺点: 三、MySQL基本语句四、DDL语句 …...
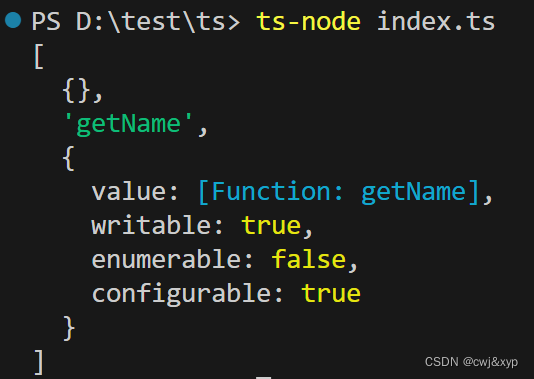
学习ts(十)装饰器
定义 装饰器是一种特殊类型的声明,它能够被附加到类声明,方法,访问符,属性或参数上,是一种在不改变原类和使用继承的情况下,动态的扩展对象功能。 装饰器使用expression形式,其中expression必须…...
如何在 Opera 中启用DNS over HTTPS
DNS over HTTPS(基于HTTPS的DNS)是一种更安全的浏览方式,但大多数 Web 浏览器默认情况下不启用它。了解如何在 Opera 浏览器中启用该功能。 您可能不知道这一点,但您的网络浏览器并不像您希望的那样私密或安全。您会看到ÿ…...

STM32 F103C8T6学习笔记13:IIC通信—AHT10温湿度传感器模块
今日学习一下这款AHT10 温湿度传感器模块,给我的OLED手环添加上测温湿度的功能。 文章提供源码、测试工程下载、测试效果图。 目录 AHT10温湿度传感器: 特性: 连接方式: 适用场所范围: 程序设计: 设…...

QT基础使用:组件和代码关联(信号和槽)
自动关联 ui文件在设计环境下,能看到的组件可以使用鼠标右键选择“转到槽”就是开始组件和动作关联。 在自动关联这个过程中软件自动动作的部分 需要对前面头文件进行保存,才能使得声明的函数能够使用。为了方便,自动关联时先对所有文件…...
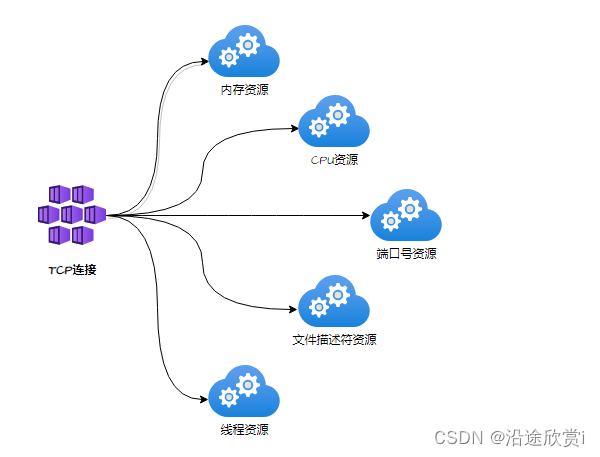
TCP最大连接数问题总结
最大TCP连接数量限制有:可用端口号数量、文件描述符数量、线程、内存、CPU等。每个TCP连接都需要以下资源,如图所示: 1、可用端口号限制 Q:一台主机可以有多少端口号?端口号与TCP连接?是否能修改&#x…...

【Docker】云原生利用Docker确保环境安全、部署的安全性、安全问题的主要表现和新兴技术产生
前言 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux或Windows操作系统的机器上,也可以实现虚拟化,容器是完全使用沙箱机制,相互之间不会有任何接口。 云原生利用Docker确保环境安全、部署的…...

explain各个字段代表的意思
id:联表查询是每个表的读取顺序,数字越大越先被读取。相同就需要通过table字段判断select_type:查询类型或者是其他操作类型(PRIMARY、UNION、UNION RESULT等)table:正在访问哪个表partitions:匹…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...
