【考研数学】矩阵、向量与线性方程组解的关系梳理与讨论
文章目录
- 引言
- 一、回顾
- 二、梳理
- 齐次线性方程组
- 非齐次线性方程组
- 写在最后
引言
两个原因让我想写这篇文章,一是做矩阵题目的时候就发现这三货经常绑在一起,让人想去探寻其中奥秘;另一就是今天学了向量组的秩,让我想起来了之前遗留下来的一个问题:到底存不存在系数矩阵的秩和增广矩阵的秩之差比 1 大的情况?可能这个问题有点抽象,不过看了下面的具体说明应该就能理解了。
一、回顾
问题起因是这样,我在写行列式的文章中关于克莱姆法则应用的说法是这样的:

有读者建议,把方程组无解的情况别写成 r ( A ) ≠ r ( A ‾ ) r(A) \ne r(\overline{A}) r(A)=r(A) ,而写成 r ( A ) + 1 = r ( A ‾ ) r(A) +1 = r(\overline{A}) r(A)+1=r(A) . 我当时还未复习到方程组和向量部分,有这样的疑问:为什么非得是相差 1 ,我如果 A A A 有很多行为 0 ,增广矩阵的秩不就可以比系数矩阵大不止 1 吗?
我当时隐约感觉是行秩和列秩模糊的问题。一方面矩阵中,我们比较常用的是初等行变换,忽视了列变换以及列秩,另一方面,列秩在方阵中和行秩是一样的。
起初我也是认为,列秩没什么用的,直到学到了向量这一部分。由于一般我们指的向量是列向量,那么由一个向量组构成的矩阵,自然考虑的是列秩。
因此我们针对一个一般性的 m × n m \times n m×n 矩阵或 n n n 个 m m m 维的向量组进行梳理,请看下文。
二、梳理
对于一般齐次线性方程组:
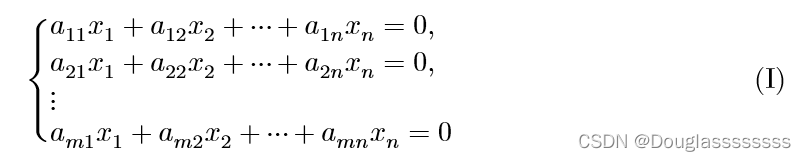
以及一般非齐次线性方程组:
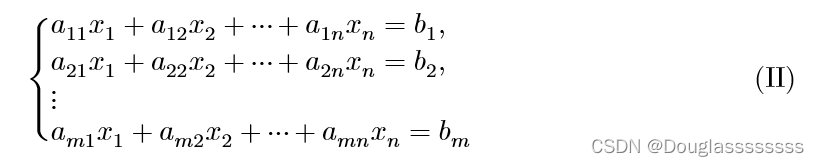
令 α 1 = ( a 11 , a 21 , … , a m 1 ) T , α 2 = ( a 12 , a 22 , … , a m 2 ) T , … , α n = ( a 1 n , a 2 n , … , a m n ) T , b = ( b 1 , b 2 , … , b m ) T \alpha_1=(a_{11},a_{21},\dots,a_{m1})^T,\alpha_2=(a_{12},a_{22},\dots,a_{m2})^T,\dots,\alpha_n=(a_{1n},a_{2n},\dots,a_{mn})^T,b=(b_{1},b_{2},\dots,b_{m})^T α1=(a11,a21,…,am1)T,α2=(a12,a22,…,am2)T,…,αn=(a1n,a2n,…,amn)T,b=(b1,b2,…,bm)T ,则方程组(I)(II)可表示为如下向量形式: x 1 α 1 + x 2 α 2 + ⋯ + x n α n = 0 ( 1.1 ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=0 (1.1) x1α1+x2α2+⋯+xnαn=0(1.1) x 1 α 1 + x 2 α 2 + ⋯ + x n α n = b ( 2.1 ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=b (2.1) x1α1+x2α2+⋯+xnαn=b(2.1)
令 X = ( x 1 , x 2 , … , x n ) T X=(x_1,x_2,\dots,x_n)^T X=(x1,x2,…,xn)T ,矩阵 A = [ α 1 , α 2 , … , α n ] A=[\alpha_1,\alpha_2,\dots,\alpha_n] A=[α1,α2,…,αn] ,即

则方程组(I)(II)可表示为如下矩阵形式: A X = 0 ( 1.2 ) AX=0(1.2) AX=0(1.2) A X = b ( 2.2 ) AX=b(2.2) AX=b(2.2)
齐次线性方程组
对于齐次线性方程组(I),它有 m m m 个约束方程, n n n 个未知数。首先我们应了解的是,不管方程个数和未知数个数多少,不可能无解,都是存在零解的。我们要讨论,就是讨论有没有非零解。我们分三种情况:
(一) m < n . m < n. m<n.
此时齐次线性方程组约束条件个数小于未知数,必有一个未知数无法受限制,如果那个不受限制的未知数取非零的话,就存在非零解。那么向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 必线性相关,则该向量组的秩 < n <n <n ,根据三秩相等性质, r ( A ) < n . r(A)<n. r(A)<n.
这种情况其实没什么好讨论的,因为肯定存在非零解,所以这也是为什么书上很少提及的情况吧。
(二) m = n . m=n. m=n.
此时就有讨论的必要了,因为方程组可能只有零解,也可能有非零解。
若齐次方程组只有零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性无关 ⇔ \Leftrightarrow ⇔ r ( A ) = n . r(A)=n. r(A)=n.
我们此时可以得出 ∣ A ∣ ≠ 0 |A| \ne 0 ∣A∣=0,即因为系数矩阵是方阵且满秩。
若齐次方程组有非零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性相关 ⇔ \Leftrightarrow ⇔ r ( A ) < n . r(A)<n. r(A)<n.
为什么是小于 n n n 呢?因为构成系数矩阵的列向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn的秩小于 n n n ,根据三秩相等性质,该矩阵的秩亦小于 n n n 。
(三) m > n . m > n. m>n.
此时约束方程个数更多,不过不影响什么。系数矩阵的秩仍然是满足 r ( A ) ≤ n , r(A) \leq n, r(A)≤n, 同样有和第 2 种情况一样的的结论。
把这三种情况总结起来,其实还是第二种情况的结论。因此不论是否是方阵,未知数和方程的个数如何,都有如下结论:即
- 齐次方程组只有零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性无关 ⇔ \Leftrightarrow ⇔ r ( A ) = n . r(A)=n. r(A)=n.
- 齐次方程组有非零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性相关 ⇔ \Leftrightarrow ⇔ r ( A ) < n . r(A)<n. r(A)<n.
非齐次线性方程组
对于非齐次线性方程组(II),它有 m m m 个约束方程, n n n 个未知数,右端常数向量为 b = ( b 1 , b 2 , … , b m ) \pmb{b=(b_1,b_2,\dots,b_m)} b=(b1,b2,…,bm)b=(b1,b2,…,bm)b=(b1,b2,…,bm) ,增广矩阵为 A ‾ = [ A ∣ b ] . \overline{A}=[A|b]. A=[A∣b].
我们从其对应的齐次线性方程组(I)出发,由于在齐次方程组中已经讨论了行数和列数的三种情况,因此在非齐次中不再分三种情况了,有兴趣同学可以也分三种情况去讨论,得到的结论应该也是一样的。
若(I)只有零解,根据上述结论,有向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性无关且 r ( A ) = n . r(A)=n. r(A)=n.
接下来我们讨论此时非齐次的情况,若非齐次线性方程组(II)无解,则向量 b \pmb{b} bbb 不能被无关的向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性表示,故增广矩阵的列向量组 α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b} α1,α2,…,αn,bα1,α2,…,αn,bα1,α2,…,αn,b 也线性无关,可得 r ( A ‾ ) = n + 1 r(\overline{A})=n+1 r(A)=n+1 . 若非齐方程组(II)有解,则向量 b \pmb{b} bbb 能被向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性表示,故增广矩阵的列向量组 α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b} α1,α2,…,αn,bα1,α2,…,αn,bα1,α2,…,αn,b 线性相关,可得 r ( A ‾ ) < n + 1 r(\overline{A})<n+1 r(A)<n+1 . 又因为向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性无关,故 r ( A ‾ ) = n = r ( A ) . r(\overline{A})=n=r(A). r(A)=n=r(A).
若方程组(II)对应的齐次方程组(I)有非零解,根据前一部分的结论,方程组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性相关且 r ( A ) < n . r(A)<n. r(A)<n.
我们讨论此时的非齐次方程组(II)的情况,若方程组(II)无解,则向量 b \pmb{b} bbb 不能被向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性表示,但由于向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 是线性相关的,故增广矩阵的列向量组 α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b} α1,α2,…,αn,bα1,α2,…,αn,bα1,α2,…,αn,b 线性相关,可得 r ( A ‾ ) < n + 1 r(\overline{A})<n+1 r(A)<n+1 且 r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
因为向量 b \pmb{b} bbb 不能被向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性表示,则向量组 α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b} α1,α2,…,αn,bα1,α2,…,αn,bα1,α2,…,αn,b 的秩比向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 多 1 ,即 r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
O.O 这个还是可以直观理解的。向量组是一列一列的,加了一列不能被原来表示的列,肯定秩加了 1 嘛。
若方程组(II)有解,则向量 b \pmb{b} bbb 能被向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αnα1,α2,…,αnα1,α2,…,αn 线性表示,故 r ( A ‾ ) = r ( A ) < n . r(\overline{A})=r(A)<n. r(A)=r(A)<n.
如下图所示,讨论了所有情况下的秩的特征

总结一下可以得到如下一般性的结论:
- 非齐次方程组有解 ⇔ \Leftrightarrow ⇔ r ( A ‾ ) = r ( A ) . r(\overline{A})=r(A). r(A)=r(A).
- 非齐次方程组无解 ⇔ \Leftrightarrow ⇔ r ( A ‾ ) ≠ r ( A ) , r(\overline{A})\ne r(A), r(A)=r(A), 或 r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
有解其实还可以再做讨论,就放在后面方程组那一章再来细说吧。
写在最后
看来还是自己疏忽了三秩相等的性质,才会产生开头那样的疑问。
现在也越来越认同,其实向量才是贯穿线性代数的重要工具。
相关文章:

【考研数学】矩阵、向量与线性方程组解的关系梳理与讨论
文章目录 引言一、回顾二、梳理齐次线性方程组非齐次线性方程组 写在最后 引言 两个原因让我想写这篇文章,一是做矩阵题目的时候就发现这三货经常绑在一起,让人想去探寻其中奥秘;另一就是今天学了向量组的秩,让我想起来了之前遗留…...
打造个人的NAS云存储-通过Nextcloud搭建私有云盘实现公网远程访问
文章目录 摘要1. 环境搭建2. 测试局域网访问3. 内网穿透3.1 ubuntu本地安装cpolar3.2 创建隧道3.3 测试公网访问 4 配置固定http公网地址4.1 保留一个二级子域名4.1 配置固定二级子域名4.3 测试访问公网固定二级子域名 摘要 Nextcloud,它是ownCloud的一个分支,是一个文件共享服…...
FFI绕过disable_functions
文章目录 FFI绕过disable_functions[RCTF 2019]NextphpPHP7.4 FFI参考 FFI绕过disable_functions [RCTF 2019]Nextphp 首先来看这道题目 index.php <?php if (isset($_GET[a])) {eval($_GET[a]); } else {show_source(__FILE__); }查看一下phpinfo 发现过滤了很多函数&…...

53 个 CSS 特效 2
53 个 CSS 特效 2 这里是第 17 到 32 个,跟上一部分比起来多了两个稍微大一点的首页布局,上篇:53 个 CSS 特效 1,依旧,预览地址在 http://www.goldenaarcher.com/html-css-js-proj/,git 地址: …...
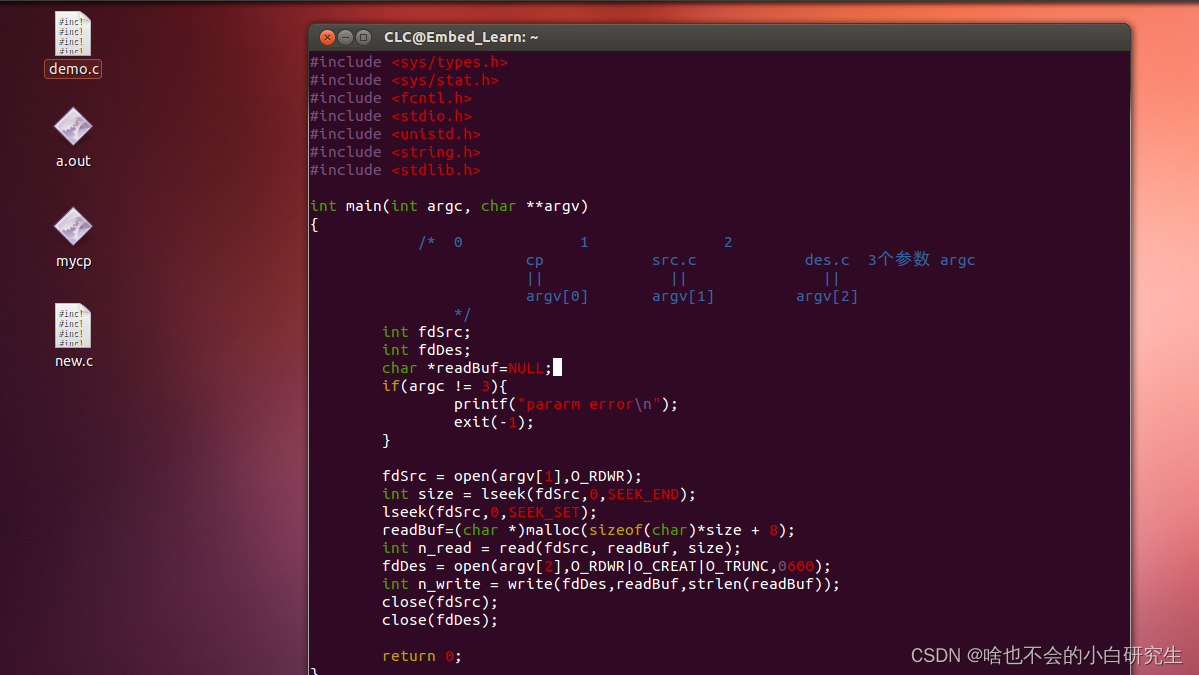
ubuntu学习(六)----文件编程实现cp指令
1 思路 Linux要想复制一份文件通常指令为: cp src.c des.c 其中src.c为源文件,des.c为目标文件。 要想通过文件编程实现cp效果,思路如下 1 首先打开源文件 src.c 2 读src到buf 3 创建des.c 4 将buf写入到des.c 5 close两个文件 2 实现 vi …...
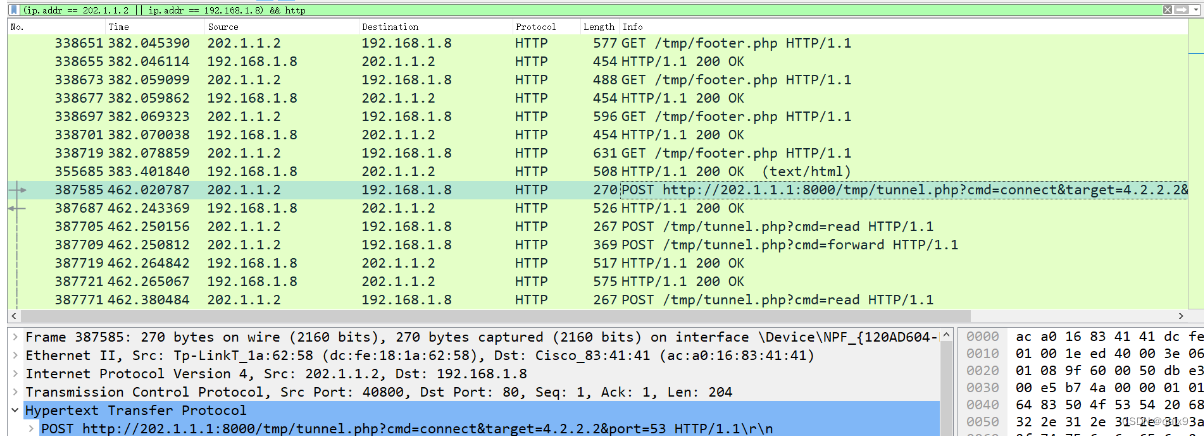
wireshark过滤器的使用
目录 wiresharkwireshark的基本使用wireshark过滤器的区别 抓包案例 wireshark wireshark的基本使用 抓包采用 wireshark,提取特征时,要对 session 进行过滤,找到关键的stream,这里总结了 wireshark 过滤的基本语法,…...

Zookeeper 脑裂问题
什么是脑裂? 脑裂(split-brain)就是“大脑分裂”,也就是本来一个“大脑”被拆分了两个或多个“大脑”,如果一个人有多个大脑,并且相互独立的话,那么会导致人体“手舞足蹈”,“不听使唤”。 脑裂通常会出现…...

计算机网络高频面试题解(一)
1. OSI七层模型 2. TCP/IP五层模型 3. TCP、UDP区别 4. TCP三次握手 5. TCP四次挥手 6. TCP状态转换图 7.TCP状态中TIME_WAIT作用 8. TCP连接建立为什么不是两次握手 9. TCP第三次握手失败会出现什么 10. TCP长连接和短链接及优缺点...

从0-1的docker镜像服务构建
文章目录 摘要一、环境准备1、docker安装2、docker-compose安装 二、镜像制作2.1、编写Dockerfile文件2.1.1、熟悉常用Dockerfile命令2.1.2、制作php镜像案例 2.2、build镜像 三、docker-compose管理容器3.1、编写docker-compose.ymal配置文件3.2、编写systemctl配置 摘要 由于…...

RabbitMQ、Kafka、RocketMQ:特点和适用场景对比
推荐阅读 AI文本 OCR识别最佳实践 AI Gamma一键生成PPT工具直达链接 玩转cloud Studio 在线编码神器 玩转 GPU AI绘画、AI讲话、翻译,GPU点亮AI想象空间 资源分享 史上最全文档AI绘画stablediffusion资料分享 AI绘画关于SD,MJ,GPT,SDXL百科全书 「java、python面试题」…...
 —— React17+React Hook+TS4 最佳实践,仿 Jira 企业级项目(二十六))
【实战】十一、看板页面及任务组页面开发(四) —— React17+React Hook+TS4 最佳实践,仿 Jira 企业级项目(二十六)
文章目录 一、项目起航:项目初始化与配置二、React 与 Hook 应用:实现项目列表三、TS 应用:JS神助攻 - 强类型四、JWT、用户认证与异步请求五、CSS 其实很简单 - 用 CSS-in-JS 添加样式六、用户体验优化 - 加载中和错误状态处理七、Hook&…...

解决docker无法执行定时任务问题
背景 在docker里面想创建定时任务,但是发现时间到了并没有执行,第一时间想到应该是没有开启crond服务,然后执行systemctl status crond.service报错如下所示: System has not been booted with systemd as init system (PID 1).…...

【FreeRTOS】【STM32】中断详细介绍
文章目录 一、三种优先级的概念辨析1. 先理清楚两个概念:CPU 和 MPU2. Cortex-M3 内核与 STM32F1XX 控制器有什么关系3. 优先级的概念辨析① Cortex-M3 内核和 STM32F1XX 的中断优先级② FreeRTOS 的任务的优先级 二、 Cortex-M3 内核的中断优先级1. 中断编号2. 优先…...
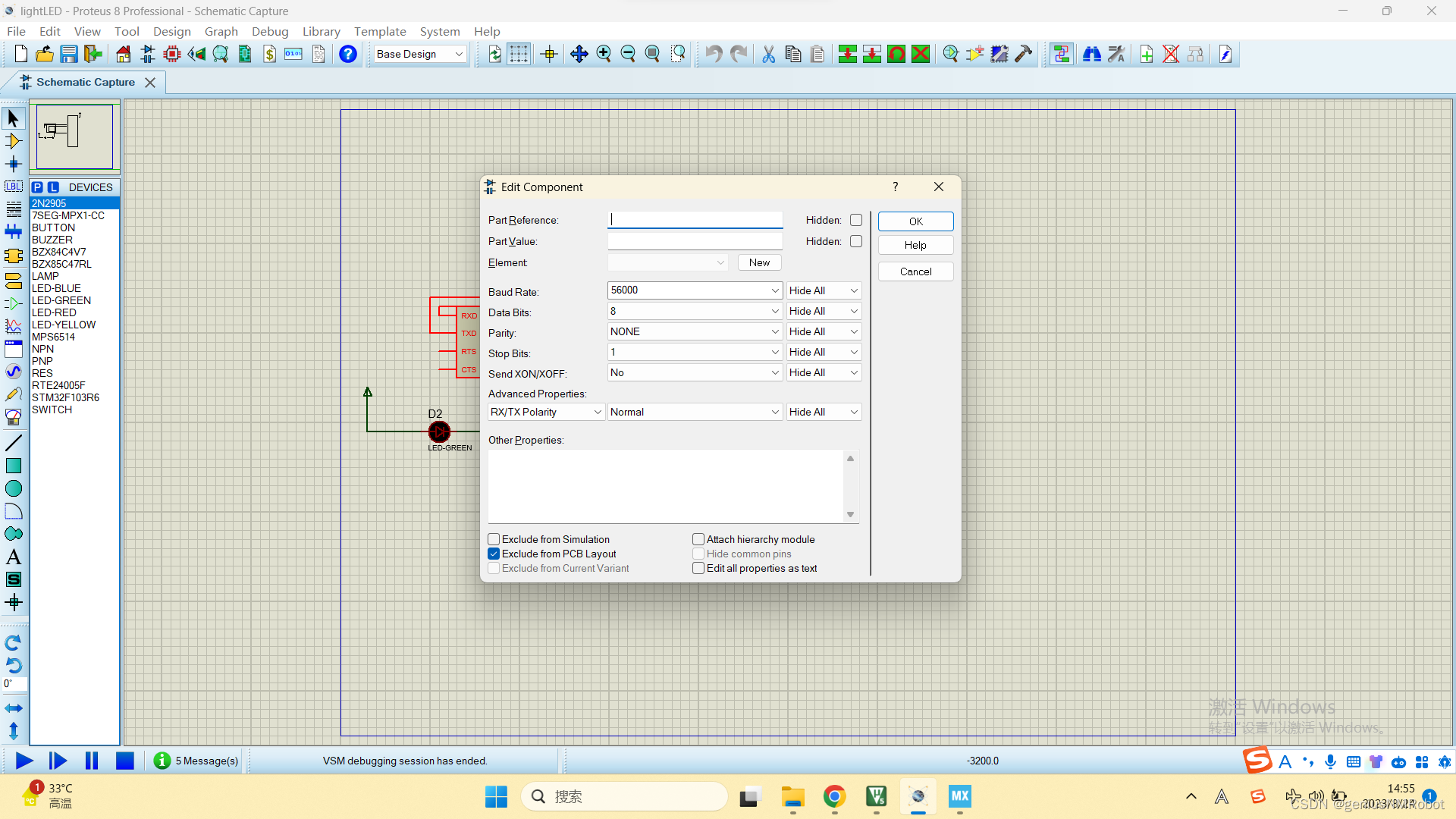
stm32串口通信(PC--stm32;中断接收方式;附proteus电路图;开发方式:cubeMX)
单片机型号STM32F103R6: 最后实现的效果是,开机后PC内要求输入1或0,输入1则打开灯泡,输入0则关闭灯泡,输入其他内容则显示错误,值得注意的是这个模拟的东西只能输入英文 之所以用2个LED灯是因为LED电阻粗略一算就是1…...
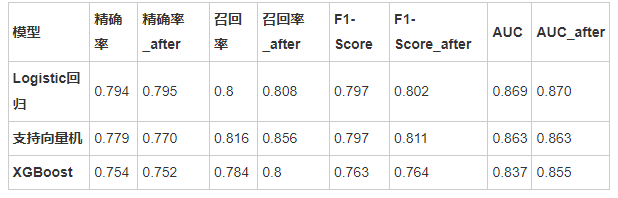
计算机毕设 基于机器学习与大数据的糖尿病预测
文章目录 1 课题背景2 数据导入处理3 数据可视化分析4 特征选择4.1 通过相关性进行筛选4.2 多重共线性4.3 RFE(递归特征消除法)4.4 正则化 5 机器学习模型建立与评价5.1 评价方式的选择5.2 模型的建立与评价5.3 模型参数调优5.4 将调参过后的模型重新进行…...
【数据结构】——查找、散列表的相关习题
目录 一、选择填空判断题题型一(顺序、二分查找的概念)题型二(分块查找的概念)题型三(关键字比较次数) 二、应用题题型一(二分查找判定树) 一、选择填空判断题 题型一(顺…...

提升Java开发效率:掌握HashMap的常见方法与基本原理
文章目录 前言一、概述1. 认识HashMap2. HashMap 的作用和重要性3. 简要讲解 HashMap 的基本原理和实现方式 二、了解 HashMap 创建及其的常见操作方法1. HashMap的创建2. 添加元素 put()3. 访问元素 get()4. 删除元素 remove()5. 计算大小 size()6. 迭代 HashMap for-each7.判…...

PostgreSQL系统概述
目录 写在前面 1.简介 1.1何为关系型数据库 1.2何为对象型数据库 2.特性 3.代码结构 3.1数据库集簇 3.2Parser查询分析流程 3.3内部查询树组成部分 3.3.1目标列表 3.4Optimizer查询优化流程 3.4.1查询计划 3.5非计划查询的SQL命令 写在前面 如有错误请指正…...
在AIGC时代的应用「中篇」)
掌握AI助手的魔法工具:解密Prompt(提示)在AIGC时代的应用「中篇」
文章目录 掌握AI助手的魔法工具:解密Prompt(提示)在AIGC时代的应用「中篇」一、指南原则1: 使用明确和具体的指令原则2: 给模型思考的时间 二、迭代三、总结与提取四、局限与改善五、总结 掌握AI助手的魔法工具:解密Prompt&#x…...

git svn:使用 git 命令来管理 svn 仓库
git-svn 使用教程 参考以下: https://cloud.tencent.com/developer/article/1415892 # 在SVN仓库上使用Git 源 https://blog.csdn.net/jiejie11080/article/details/106917116 # git svn clone速度慢的解决办法 http://blog.chinaunix.net/uid-11639156-id-30774…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...
Axure零基础跟我学:展开与收回
亲爱的小伙伴,如有帮助请订阅专栏!跟着老师每课一练,系统学习Axure交互设计课程! Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题:Axure菜单展开与收回 课程视频:...

深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀”
深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀” 在JavaScript中,我们经常需要处理文本、数组、对象等数据类型。但当我们需要处理文件上传、图像处理、网络通信等场景时,单纯依赖字符串或数组就显得力不从心了。这时ÿ…...
