【算法】双指针求解盛最多水的容器

Problem: 11. 盛最多水的容器
文章目录
- 题目解析
- 算法原理讲解
- 复杂度
- Code
题目解析
首先我们来解析一下本题
题目中说到,要找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
- 那我们现在来看最外侧的两根,一个高度为8,一个则为7,那我们肯定选择高度为7的,如果选择8的话就会出现溢出的问题;我们这里要求解的是可以容纳多少的水分,所以便要计算的是【容量】,那从第一根柱子到第八根的距离是多少呢?即
8 - 1 = 7 - 所以最后的容量即为
7 * 7 = 49
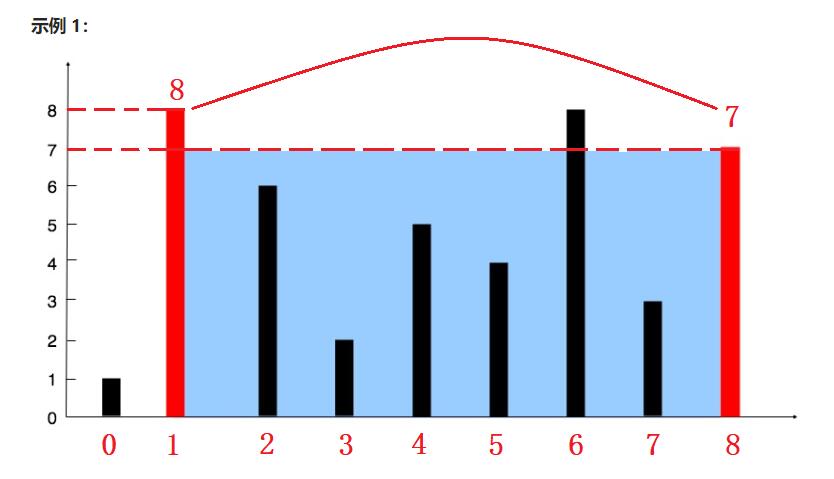
- 那我们再来看一个,高度取小的那个为6,宽度则取4,所以最后的容积为
4 * 6 = 24,比49要来的小,但我们要取的是最大的那一个容量,所以还是取 49
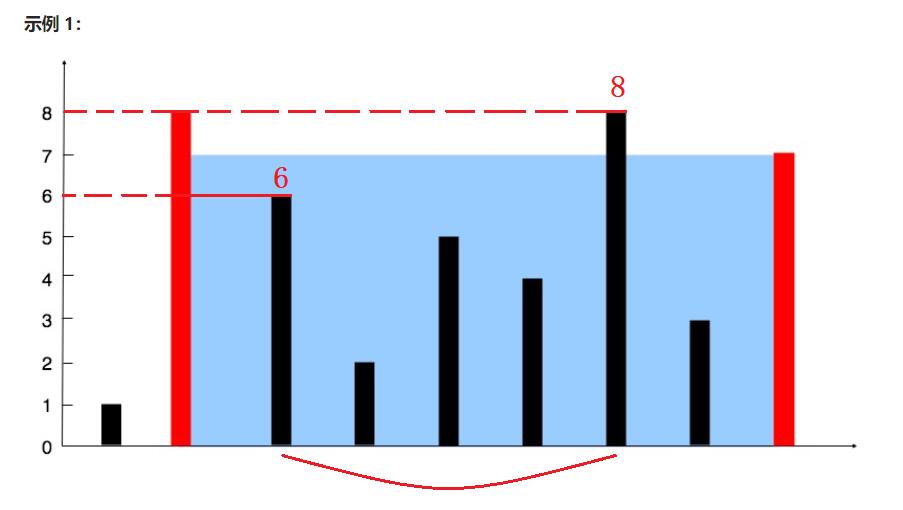
💬 所以对于本题来说,我们初步的想法就是不断地去找两根柱子,然后计算出这两根柱子之间的所围成的容积大小,最后我们所要的则是最大的那一个容积
算法原理讲解
接下去呢我们再来讲解一下本题的算法原理
- 首先的话来讲解一下第一种方法,那就是我们同学最喜欢使用的【暴力枚举】,因为我们是不断地一一比较,所以直接使用双层for循环去进行实现即可。不过呢这种写法我试了一下是会超时的,所以立马放弃❌

- 接下去第二种,也是我要进行重点讲解的,那利用单调性,然后使用【双指针】来进行求解。因为我们在对两根柱子不断进行比较的时候,数字都会不停地发生变化,那么这里就会有两个情况:
- 第一种呢是比较的数字开始出现缩减的情况,即
w变小;而且距离也开始缩减,即h变小,那w和h都进行缩减的话,最后的乘积[v]也会变得小 - 第二种的话则是所计算的数据不变,新的数据发生了放大,所以呢
h不会缩小,不过距离的话还是会发生缩减,此时整体[v]也会变得小
- 第一种呢是比较的数字开始出现缩减的情况,即

那根据上面的分析,我们呢可以使用双指针去模拟遍历两个x轴的数据
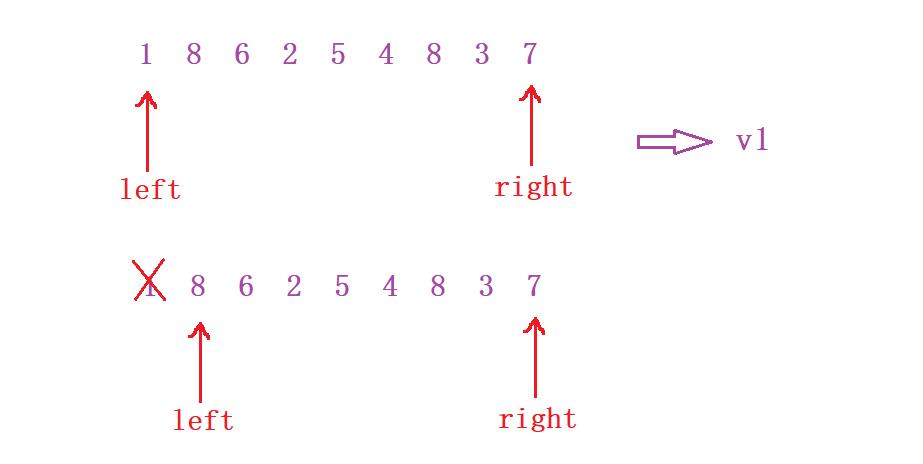
- 看到下面我们直接从两侧开始进行计算,那么在计算完得出第一个容量
v1后,我们便可以直接舍弃这个【1】,因为其再与任何结合计算都会比【1】与【7】要来得小,原因在于距离会发生一个缩减
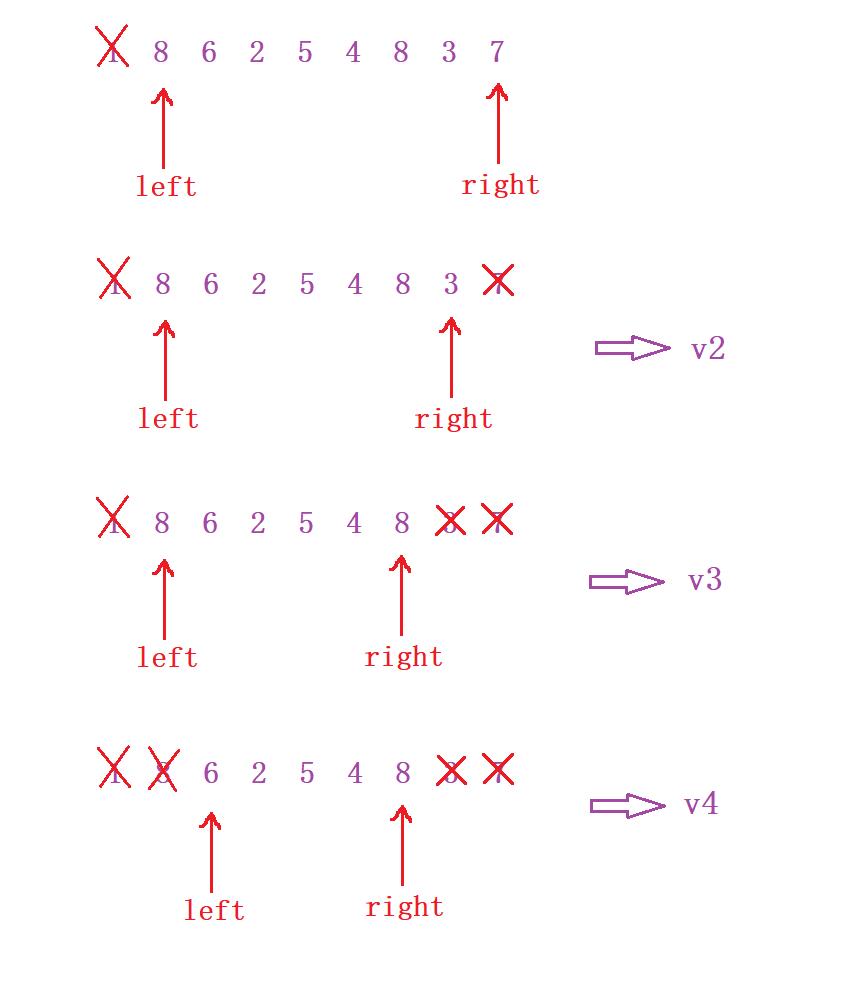
- 那接下去还是一样的思路,我们在使用双指针进行遍历的时候,只需要去判断二者的大小即可,左侧小的话就右移,右侧小的话就左移,然后记录下每一个容量
v1、v2、v3,最后的话再去做一个比较即可
复杂度
- 时间复杂度:
对于时间复杂度而言,因为我们就是使用左右指针在遍历原先的数组,所以呢复杂度即为 O ( n ) O(n) O(n)
- 空间复杂度:
因为没开辟多余的空间,所以空间复杂度, 示例: O ( 1 ) O(1) O(1)
Code
以下是代码展示,读者可以根据我上面所分析的思路,自行去书写一下代码
- 可以看到,我在这里定义两个左右指针
left和right,然后呢通过循环去遍历并计算它们两个位子上的数,计算的方法就是我们上面所讲,记住要去不断地更新最大值 - 当一轮计算完成之后不要忘记去更新
left和right。最后当这个循环结束再去返回计算出来的最大值即可。
class Solution {
public:int maxArea(vector<int>& height) {int left = 0, right = height.size() - 1;int ret = 0;while(left < right){int v = min(height[left], height[right]) * (right - left);ret = max(v, ret); // 更新最大值if(height[left] < height[right]) left++;else right--;}return ret;}
};

相关文章:

【算法】双指针求解盛最多水的容器
Problem: 11. 盛最多水的容器 文章目录 题目解析算法原理讲解复杂度Code 题目解析 首先我们来解析一下本题 题目中说到,要找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 那我们现在来看最外侧的两根,一个高度为8&#…...
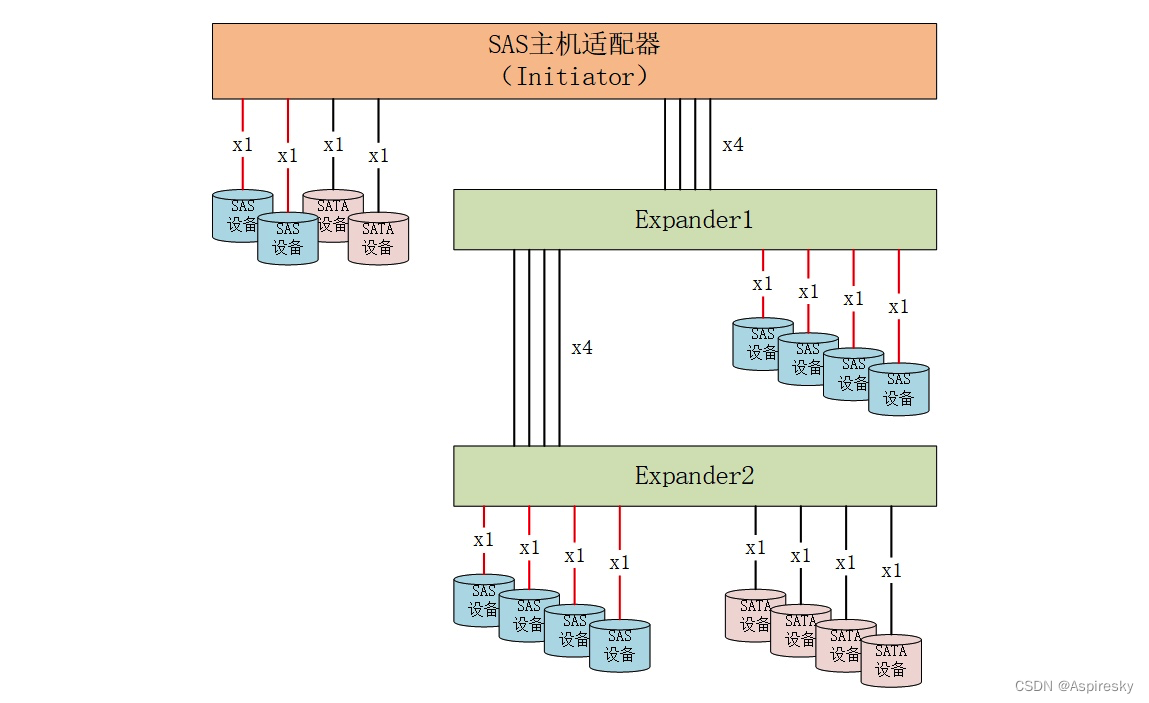
浅析SAS协议:设备接入与探测
文章目录 SAS设备初始化OOB信号SAS设备间OOB交互场景一:SAS设备两边同时发送SAS COMINIT信号场景二:SAS设备A先发送COMINIT信号场景三:SAS设备B错过COMINIT信号 SAS与SATA设备间OOB交互场景一:SATA设备未响应COMSAS信号场景二&…...

RISC-V IOPMP实际用例-Andes SoC‘s Rapid-k模型
安全之安全(security)博客目录导读 2023 RISC-V中国峰会 安全相关议题汇总 说明:本文参考RISC-V 2023中国峰会如下议题,版权归原作者所有。...

【高阶数据结构】哈希表详解
文章目录 前言1. 哈希的概念2. 哈希冲突3. 哈希函数3.1 直接定址法3.2 除留余数法--(常用)3.3 平方取中法--(了解)3.4 折叠法--(了解)3.5 随机数法--(了解)3.6 数学分析法--(了解) 4. 哈希冲突的解决方法及不同方法对应的哈希表实现4.1 闭散列(开放定址法࿰…...

C#与西门子PLC1500的ModbusTcp服务器通信4--搭建ModbusTcp客户端
1、客户端选择 客户端可以是一个程序或一个设备,这里我以C#WINFORM程序来实现客户机与PLC的Modbustcp服务器通信,开发环境是VS2019,.NET Framework版本是4.7.2 2、创建winform程序 3、引入Nmodbus4协议 找到项目,找到引用&…...

性能调优篇 二、Jvm监控及诊断工具-命令行篇
目录 一、概述1、简单命令行工具 二、jps:查看正在运行的Java程序(掌握)1、是什么?2、测试3、基本语法 三、jstat:查看jvm统计信息(掌握)1、是什么?2、基本语法3、补充 四、jinfo&am…...
Fooocus启动时modules报错的解决方法
原理:是由于其他程序的安装导致modules的版本不对,先卸载现有版本,再运行run.bat让其自动安装响应的modules版本。 1、cmd运行windows dos终端。 2、将Fooocus_win64_1-1-1035文件夹备份,rename为Fooocus_win64_1-1-1035backup文…...

RSA私钥解密操作
RSA私钥解密操作 一、背景二、操作三、常见问题3.1 invalid key format3.2 解密的数据太长3.3 Decryption error 一、背景 项目数据库中存放的敏感字段已使用rsa加密的方式,将内容加密成密文存放, 现在需要在使用的时候,使用私钥进行解密。 二、操作 …...

数据库基本知识
基本概念 数据 描述事物的符号记录称为数据,数字,文字,图形,图像,声音,档案记录等都是数据 数据是以“记录”的形式按照统一的格式进行存储的,而不是杂乱无章的 相同格式和类型的数据统一存…...

使用Redis统计网站的UV/DAU
HyperLogLog/BitMap 统计UV、DAU需要用到Redis的高级数据类型 M public class RedisKeyUtil {private static final String PREFIX_UV "uv";private static final String PREFIX_DAU "dau";// a single days UVpublic static String getUVKey(String …...

【python】报错:ImportError: DLL load failed: 找不到指定的模块 的详细解决办法
原因:安装的包与python版本不一致 解决方法: 查看python版本: #python / #python -V Python 3.7.9 (tags/v3.7.9:13c94747c7, Aug 17 2020, 18:58:18) [MSC v.1900 64 bit (AMD64)] on win32只查看python第三方模块(库、包&…...

SemrushBot蜘蛛爬虫屏蔽方式
查看访问日志时候发现有SemrushBot爬虫 屏蔽方法: 使用robots.txt文件是一种标准的协议,用于告诉搜索引擎哪些页面可以和不能被爬取,如想禁止Googlebot爬取整个网站的话,可以在该文件中添加以下内容: User-agent: Googlebot Disallow: / 对于遵循robots协议的蜘蛛…...

6 ssh面密登录
1. 首先进入自己的家目录,执行命令 [atguiguhadoop102 .ssh]$ ssh-keygen -t rsa然后敲(三个回车),就会生成两个文件id_rsa(私钥)、id_rsa.pub(公钥) 2. 将公钥拷贝到要免密登录的…...
基于微信小程序的汽车租赁系统的设计与实现ljx7y
汽车租赁系统,主要包括管理员、用户二个权限角色,对于用户角色不同,所使用的功能模块相应不同。本文从管理员、用户的功能要求出发,汽车租赁系统系统中的功能模块主要是实现管理员后端;首页、个人中心、汽车品牌管理、…...
优化学习体验的在线考试系统
随着互联网的发展,在线教育逐渐成为学习的主要方式之一。在线考试系统作为在线教育的重要组成部分,对于学习者提供了更为便捷和灵活的学习方式。但是,如何优化学习体验,提高学习效果,仍然是在线考试系统需要解决的问题…...

1267. 统计参与通信的服务器
题目描述: 这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有。 如果两台服务器位于同一行或者同一列,我们就认为它们之间可以进行通信。 请你统计并返回能…...

【考研数学】矩阵、向量与线性方程组解的关系梳理与讨论
文章目录 引言一、回顾二、梳理齐次线性方程组非齐次线性方程组 写在最后 引言 两个原因让我想写这篇文章,一是做矩阵题目的时候就发现这三货经常绑在一起,让人想去探寻其中奥秘;另一就是今天学了向量组的秩,让我想起来了之前遗留…...
打造个人的NAS云存储-通过Nextcloud搭建私有云盘实现公网远程访问
文章目录 摘要1. 环境搭建2. 测试局域网访问3. 内网穿透3.1 ubuntu本地安装cpolar3.2 创建隧道3.3 测试公网访问 4 配置固定http公网地址4.1 保留一个二级子域名4.1 配置固定二级子域名4.3 测试访问公网固定二级子域名 摘要 Nextcloud,它是ownCloud的一个分支,是一个文件共享服…...
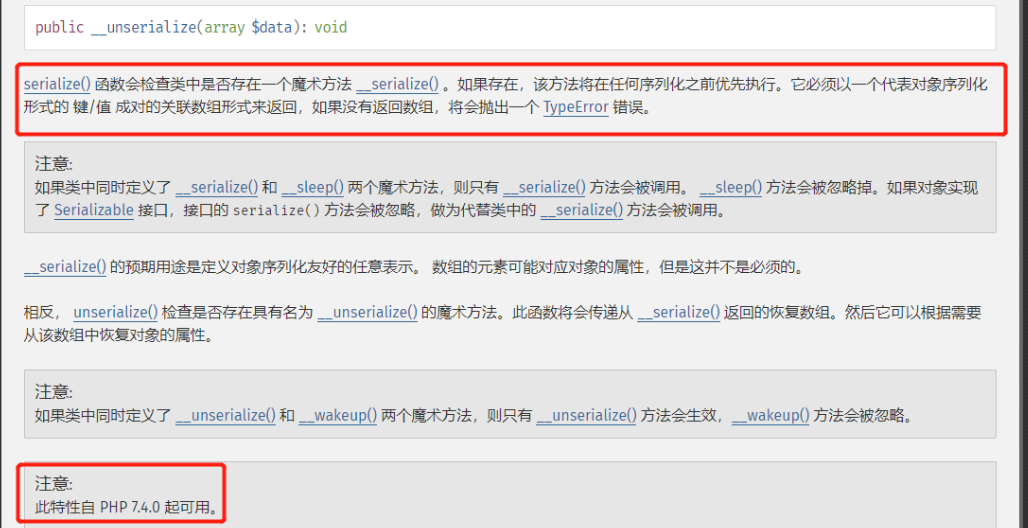
FFI绕过disable_functions
文章目录 FFI绕过disable_functions[RCTF 2019]NextphpPHP7.4 FFI参考 FFI绕过disable_functions [RCTF 2019]Nextphp 首先来看这道题目 index.php <?php if (isset($_GET[a])) {eval($_GET[a]); } else {show_source(__FILE__); }查看一下phpinfo 发现过滤了很多函数&…...

53 个 CSS 特效 2
53 个 CSS 特效 2 这里是第 17 到 32 个,跟上一部分比起来多了两个稍微大一点的首页布局,上篇:53 个 CSS 特效 1,依旧,预览地址在 http://www.goldenaarcher.com/html-css-js-proj/,git 地址: …...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
