基于相空间重构的混沌背景下微弱信号检测算法matlab仿真,对比SVM,PSO-SVM以及GA-PSO-SVM
目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
4.1 SVM
4.2 PSO-SVM
4.3 GA-PSO-SVM
5.算法完整程序工程
1.算法运行效果图预览
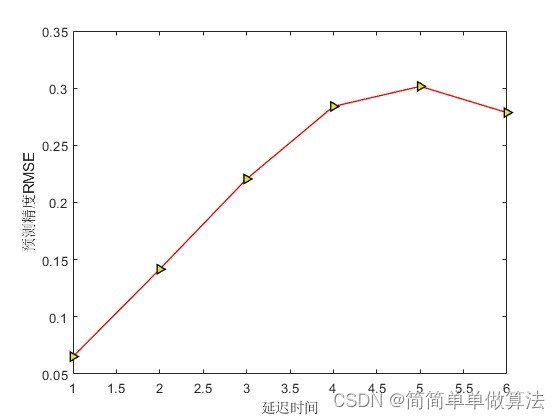
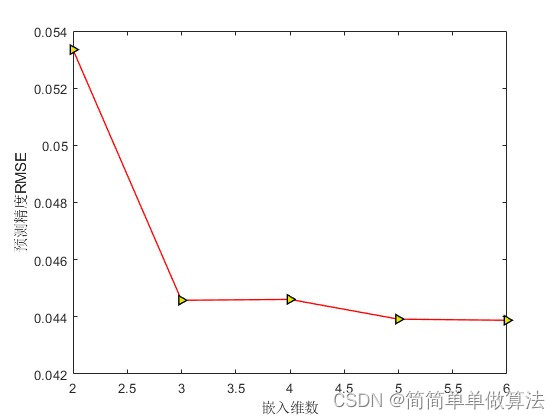
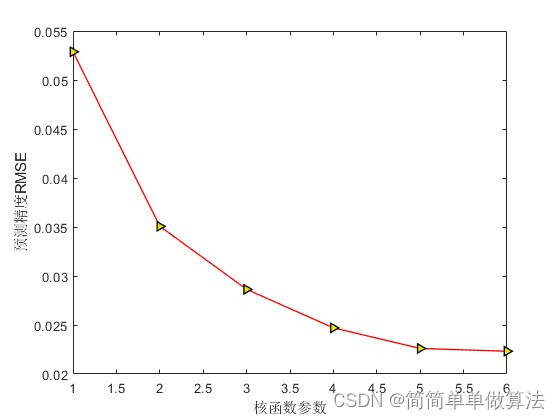
SVM:

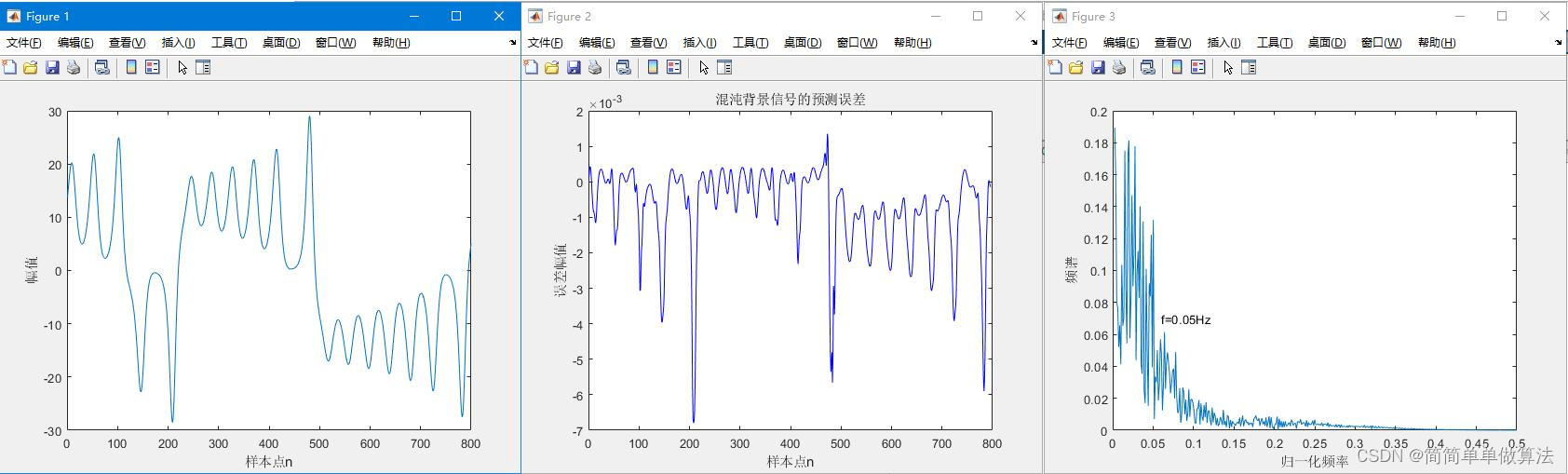
PSO-SVM:
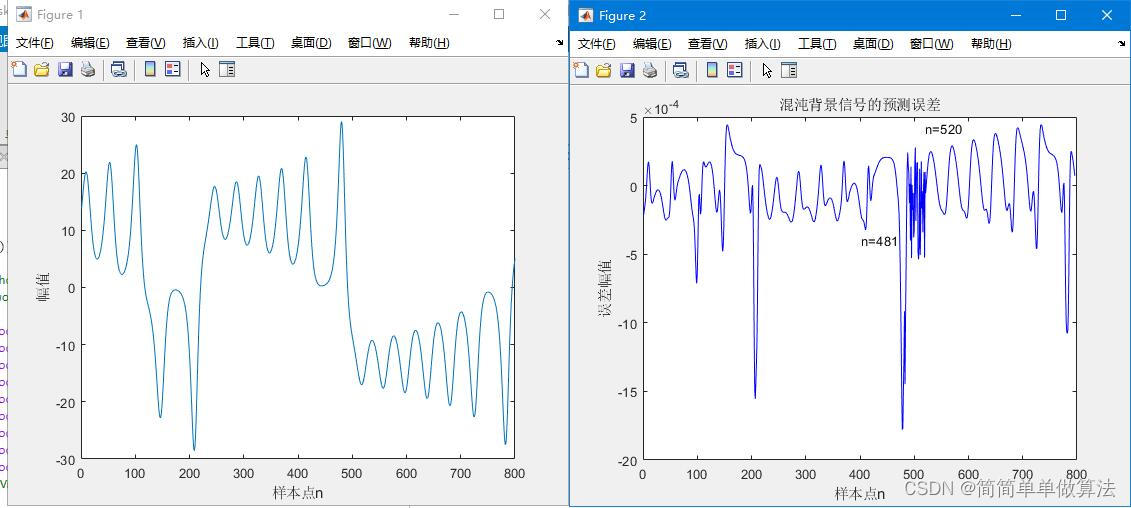
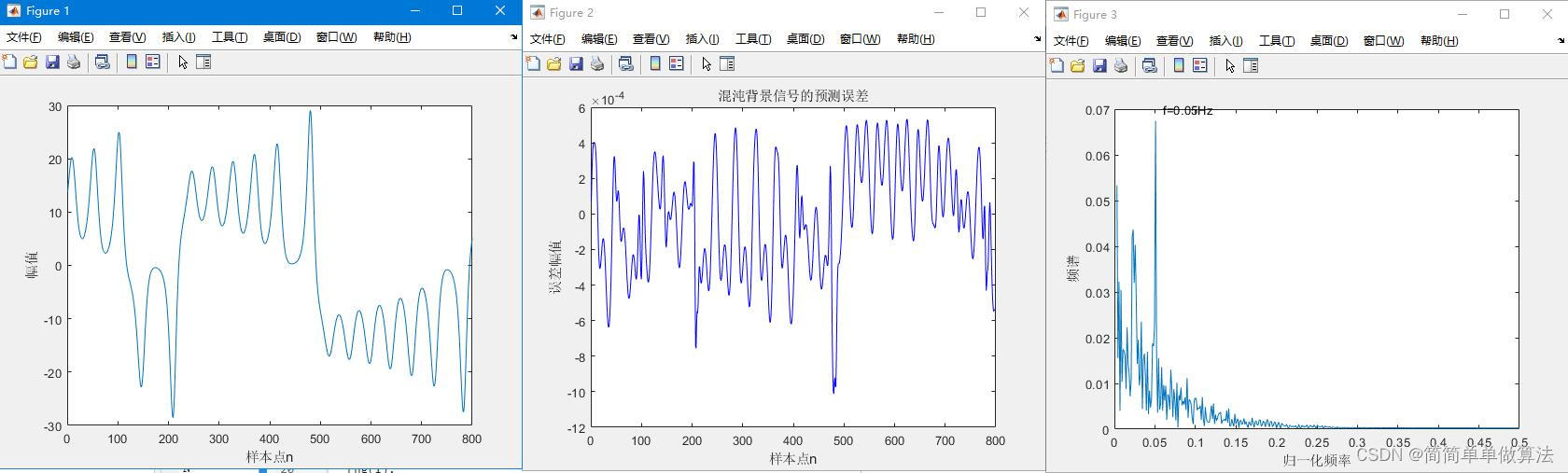
GA-PSO-SVM:
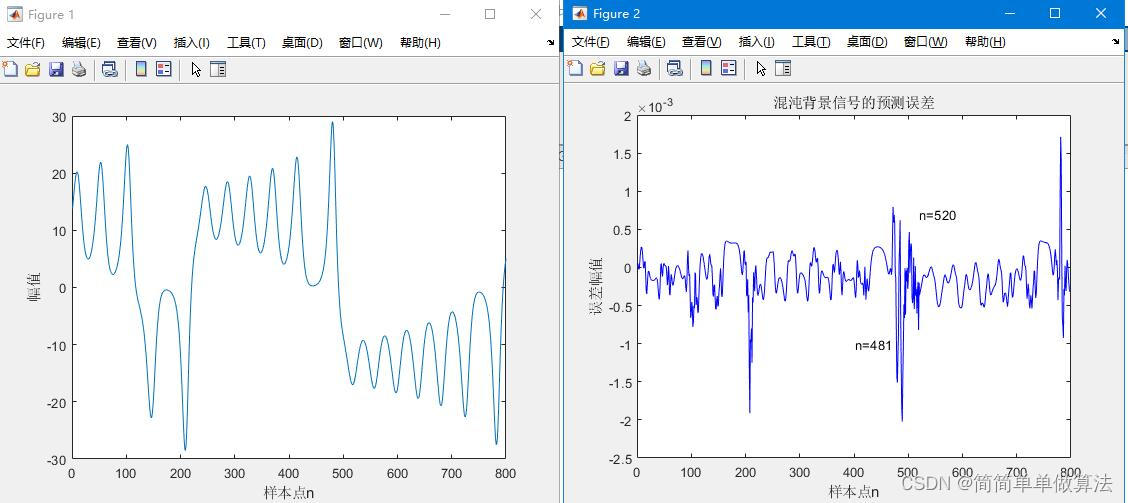
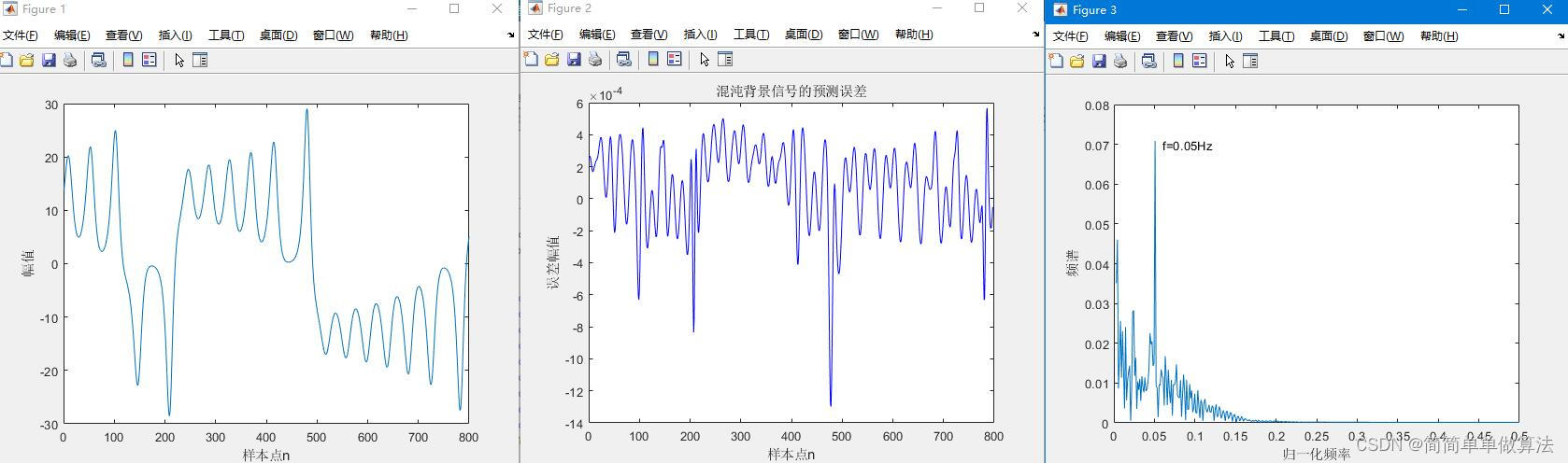 以上仿真图参考文献《基于相空间重构的混沌背景下微弱信号检测方法研究》
以上仿真图参考文献《基于相空间重构的混沌背景下微弱信号检测方法研究》
2.算法运行软件版本
MATLAB2022a
3.部分核心程序
................................................
while gen < MAXGEN; genw = wmax-gen*(wmax-wmin)/MAXGEN;FitnV = ranking(Objv); Selch = select('sus',Chrom,FitnV); Selch = recombin('xovsp',Selch,0.9); Selch = mut(Selch,0.1); phen1 = bs2rv(Selch,FieldD); %基于粒子群的速度更新for i=1:1:NINDif gen > 1va(i) = w*va(i) + c1*rand(1)*(phen1(i,1)-taos2) + c2*rand(1)*(taos-taos2);vb(i) = w*vb(i) + c1*rand(1)*(phen1(i,2)-ms2) + c2*rand(1)*(ms-ms2);vc(i) = w*vc(i) + c1*rand(1)*(phen1(i,3)-Cs2) + c2*rand(1)*(Cs-Cs2);vd(i) = w*vd(i) + c1*rand(1)*(phen1(i,4)-gammas2) + c2*rand(1)*(gammas-gammas2);elseva(i) = 0;vb(i) = 0;vc(i) = 0;vd(i) = 0;endendfor a=1:1:NIND Data1(a,:) = phen1(a,:); tao = round(Data1(a,1) + 0.15*va(i));%遗传+PSOm = round(Data1(a,2) + 0.15*vb(i));C = Data1(a,3) + 0.15*vc(i);gamma = Data1(a,4) + 0.15*vd(i);if tao >= max1tao = max1;endif tao <= min1tao = min1;end if m >= max2m = max2;endif m <= min2m = min2;end if C >= max3C = max3;endif C <= min3C = min3;end if gamma >= max4gamma = max4;endif gamma <= min4gamma = min4;end %计算对应的目标值[epls,tao,m,C,gamma] = func_fitness(X_train,X_test,tao,m,C,gamma);E = epls;JJ(a,1) = E;end Objvsel=(JJ); [Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel); gen=gen+1; %保存参数收敛过程和误差收敛过程以及函数值拟合结论Error(gen) = mean(JJ);pause(0.2);[V,I] = min(Objvsel);JI = I;tmpps = Data1(JI,:);taos2 = round(tmpps(1));ms2 = round(tmpps(2));Cs2 = tmpps(3);gammas2 = tmpps(4);
end [V,I] = min(Objvsel);
JI = I;
tmpps = Data1(JI,:);
tao0 = round(tmpps(1));
m0 = round(tmpps(2));
C0 = tmpps(3);
gamma0 = tmpps(4);%save GAPSO.mat tao0 m0 C0 gamma0
endif SEL == 2
load GAPSO.mat
%调用四个最优的参数
tao = tao0;
m = m0;
C = C0;
gamma = gamma0;%先进行相空间重构
[Xn ,dn ] = func_CC(X_train,tao,m);
[Xn1,dn1] = func_CC(X_test,tao,m);t = 1/1:1/1:length(dn1)/1;
f = 0.05;
sn = 0.0002*sin(2*pi*f*t);
%叠加
dn1 = dn1 + sn';%SVM训练%做单步预测
cmd = ['-s 3',' -t 2',[' -c ', num2str(C)],[' -g ',num2str(gamma)],' -p 0.000001'];
model = svmtrain(dn,Xn,cmd);
%SVM预测
[Predict1,error1] = svmpredict(dn1,Xn1,model);
RMSE = sqrt(sum((dn1-Predict1).^2)/length(Predict1));
Err = dn1-Predict1;
%误差获取
clc;
RMSE figure;
plot(Err,'b');
title('混沌背景信号的预测误差');
xlabel('样本点n');
ylabel('误差幅值');Fs = 1;
y = fftshift(abs(fft(Err)));
N = length(y)
fc = [-N/2+1:N/2]/N*Fs;figure;
plot(fc(N/2+2:N),y(N/2+2:N));
xlabel('归一化频率');
ylabel('频谱');
text(0.06,0.07,'f=0.05Hz');end
07_006m
4.算法理论概述
4.1 SVM
支持向量机(Support Vector Machine,SVM)是一种用于分类和回归的机器学习方法,其原理基于寻找一个最优超平面(或者曲线在非线性情况下)来划分不同类别的数据点。SVM 的目标是找到一个能够最大化不同类别之间的间隔(margin)的超平面,从而在未知数据上取得良好的泛化能力。
SVM 的目标是找到一个超平面,使得距离超平面最近的数据点(支持向量)到超平面的距离(间隔)最大。这个间隔可以用数据点到超平面的函数距离来表示,即:

SVM 的目标是解决以下优化问题:

在非线性情况下,SVM 可以通过引入核函数将数据从原始特征空间映射到高维特征空间,从而找到一个在高维空间中的超平面来进行分类。常见的核函数包括线性核、多项式核、高斯核(RBF核)等。
总结起来,SVM 的原理在于寻找一个最优的超平面或曲线,使得不同类别之间的间隔最大化,从而实现分类任务。它的优势在于能够处理高维数据、非线性问题,并且在一定程度上能够抵抗过拟合。
4.2 PSO-SVM
在将PSO应用于SVM的优化过程中,我们主要关注SVM的超参数,如核函数类型、正则化参数C等。PSO算法可以帮助我们找到一组超参数,使得SVM在训练数据上的性能最佳。

在PSO-SVM中,适应度函数通常是SVM在训练集上的性能指标,如准确率、F1分数等。通过PSO算法优化SVM的超参数,可以帮助我们找到一组最优的超参数配置,从而提高SVM在分类问题中的性能表现。这种方法可以在一定程度上自动搜索超参数空间,避免了手动调整的繁琐过程。
4.3 GA-PSO-SVM
GA-PSO结合了遗传算法的群体进化和粒子群优化的局部搜索能力。遗传算法通过模拟生物进化的过程,通过交叉、变异等操作对种群中的个体进行优化。粒子群优化模拟了鸟群或鱼群等自然界中群体行为,通过个体历史最优和群体历史最优来调整粒子的位置。
在将GA-PSO应用于SVM的优化过程中,我们主要关注SVM的超参数,如核函数类型、正则化参数C等。GA-PSO算法可以帮助我们在超参数空间中搜索到更优的解,以提高SVM在训练数据上的性能。GA-PSO的公式包括遗传算法的选择、交叉和变异操作,以及粒子群优化的速度和位置更新公式。这些公式可以根据具体的算法变体进行调整。
总体而言,GA-PSO算法将遗传算法和粒子群优化结合起来,通过遗传算法的全局搜索和粒子群优化的局部搜索,以及SVM的性能评估,实现对SVM超参数的优化。这种方法可以更全面地搜索超参数空间,从而提高SVM在分类问题中的性能。
5.算法完整程序工程
OOOOO
OOO
O
相关文章:

基于相空间重构的混沌背景下微弱信号检测算法matlab仿真,对比SVM,PSO-SVM以及GA-PSO-SVM
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1 SVM 4.2 PSO-SVM 4.3 GA-PSO-SVM 5.算法完整程序工程 1.算法运行效果图预览 SVM: PSO-SVM: GA-PSO-SVM: 以上仿真图参考文献《基于相空间重构的混沌背景下微弱信号检测方法研究》 2.…...

开发者必备:推荐将闲置iPad Pro打造为编程工具,使用VS Code编写代码
文章目录 前言1. 本地环境配置2. 内网穿透2.1 安装cpolar内网穿透(支持一键自动安装脚本)2.2 创建HTTP隧道 3. 测试远程访问4. 配置固定二级子域名4.1 保留二级子域名4.2 配置二级子域名 5. 测试使用固定二级子域名远程访问6. iPad通过软件远程vscode6.1 创建TCP隧道 7. ipad远…...

c++,标准库std中全局函数 _Destroy_in_place(...)的分析
(1)该函数的定义和位置如下: 可见,传入形参为某种类型的引用,该函数会执行形参的析构函数,还可以有效解决数组的连续析构。很强大的函数。 (2)疑问是,若形参是指针类型…...

java:Tomcat
文章目录 背景服务器web 服务器服务资源的分类服务器软件的分类nginx 和 tomact总结 安装Tomcatbrew安装官网压缩包安装IDEA集成IDEA插件 说明 背景 在讲 Tomcat 是啥之前,我们先来了解一些概念。 服务器 可以理解为一个高性能的电脑,但是这个电脑现在…...

US-P2F-R-C双线圈插头式比例阀放大器
US-P2F-R-C型插头式安装比例放大器控制不带电反馈的单或双比例电磁铁的比例阀,如比例插装阀、比例方向阀、比例压力阀、比例流量阀、比例叠加阀等,带数显区显示及当前参数,如指令、电流、上下斜坡、颤振频率等,指令类型兼容0-10V、…...

clickhouse一次异常排查记录
clickhouse中报错 关闭了自启动,删了status,重启了clickhouse还是报错 1,排查定时执行的脚本日志(每小时第5分钟执行) INSERT INTO quality0529.previously_reported_urls (url) SELECT url FROM quality0529.hourly_…...

Python 数据可视化:玩转 Matplotlib 的散点图、线形图、饼图和热力图
前言 我们来探讨其他几种常用的数据可视化图形:散点图、线形图、饼图和热力图。 可视化图形的优点~ 数据可视化图表是数据分析和演示的重要手段,它有以下优点: 快速理解信息:通过图表,人们可以迅速捕捉到数据的主要模式和趋势,而不需要详细查看每个数据点。 增强记忆:…...
基于python+pyqt实现opencv银行卡身份证等识别
效果展示 识别结果 查看处理过程 历史记录 完整演示视频: 无法粘贴视频........ 完整代码链接 视频和代码都已上传百度网盘,放在主页置顶文章...
惠普台式机装系统记录
1. 问题集锦 1.必须装双系统,就是必须得有win系统,不然会出现蓝屏; 2.装win系统之后,再装ubuntu系统,会出现rst的问题,基本无解,放弃; 2. 装机步骤: 第一步:…...

java八股文面试[JVM]——垃圾回收
参考:JVM学习笔记(一)_卷心菜不卷Iris的博客-CSDN博客 GC垃圾回收面试题: JVM内存模型以及分区,需要详细到每个区放什么 堆里面的分区:Eden,survival from to,老年代,各…...

iOS开发Swift-控制流
1.For-In循环 //集合循环 let names ["a", "b", "c"] for name in names {print("Hello, \(name)!") } //次数循环 for index in 1...5{print("Hello! \(index)") } //不需要值时可以使用 _ 来忽略此值 for _ in 1...5{…...

leetcode875. 爱吃香蕉的珂珂(java)
二分查找 爱吃香蕉的珂珂二分查找 上期经典 爱吃香蕉的珂珂 难度 - 中等 LC - 875.爱吃香蕉的珂珂 珂珂喜欢吃香蕉。这里有 n 堆香蕉,第 i 堆中有 piles[i] 根香蕉。警卫已经离开了,将在 h 小时后回来。 珂珂可以决定她吃香蕉的速度 k (单位&…...

LeetCode-406-根据身高重建队列
题目描述: 假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。 请你重新构造…...
JVM——类加载与字节码技术—编译期处理+类加载阶段
3.编译期处理 编译期优化称为语法糖 3.1 默认构造器 3.2 自动拆装箱 java基本类型和包装类型之间的自动转换。 3.3泛型集合取值 在字节码中可以看见,泛型擦除就是字节码中的执行代码不区分是String还是Integer了,统一用Object. 对于取出的Object&…...
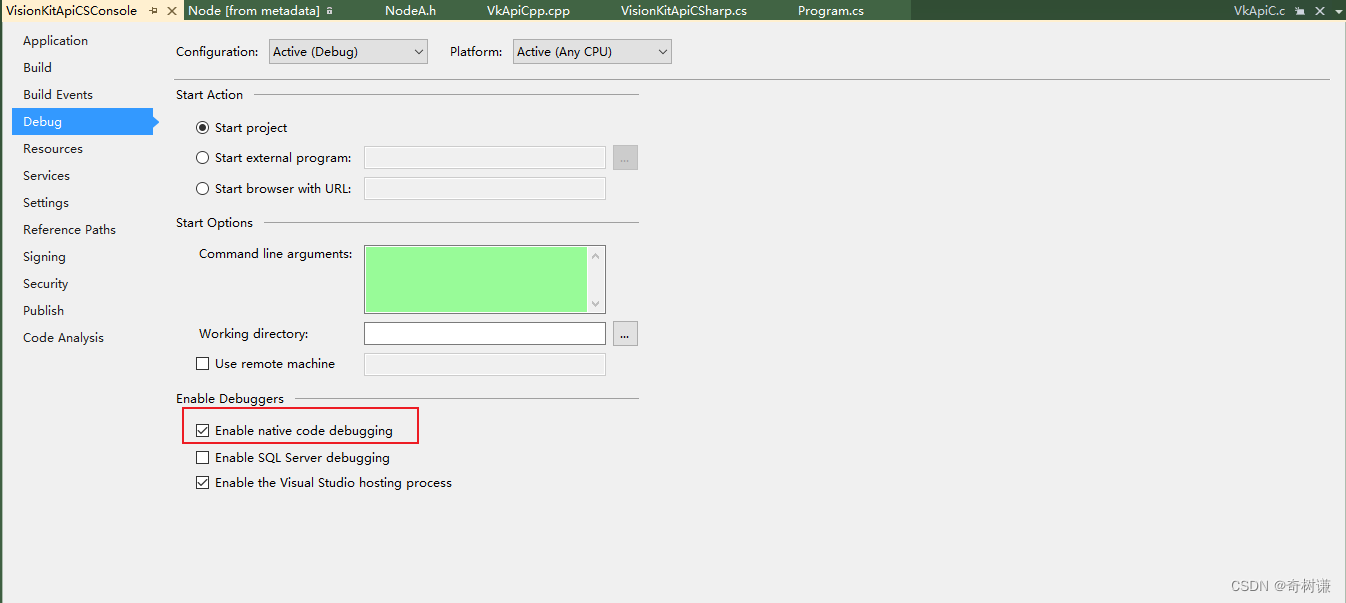
C#|如何调试进依赖动态库中
第一步:打开项目属性 第二步 打开debug的本地调试可用 第三步 把要调试的代码拖进主界面打断点就可以进断点了...
全新版本QStack云管系统3.5.3 附详细安装教程
源码介绍: QStack云管系统3.5.3,全新版本下载安装包详细搭建教程。 涵盖了服务器、云主机、代理IP等多种云产品管理运维和安全存储。 同时,QStack还支持对接运营众多公有云厂商产品资源,满足不同用户的需求。 通过开放API和插…...

SLB 负载均衡
优质博文:IT-BLOG-CN 一、简介 SLB (Server Loader Balancer)将访问流量根据转发策略分发到后台多台服务器的流量分发控制服务,来实现多台服务器提供相同的业务服务。负载均衡扩展了应用的服务能力,增强了应用的可用性。主要用于…...
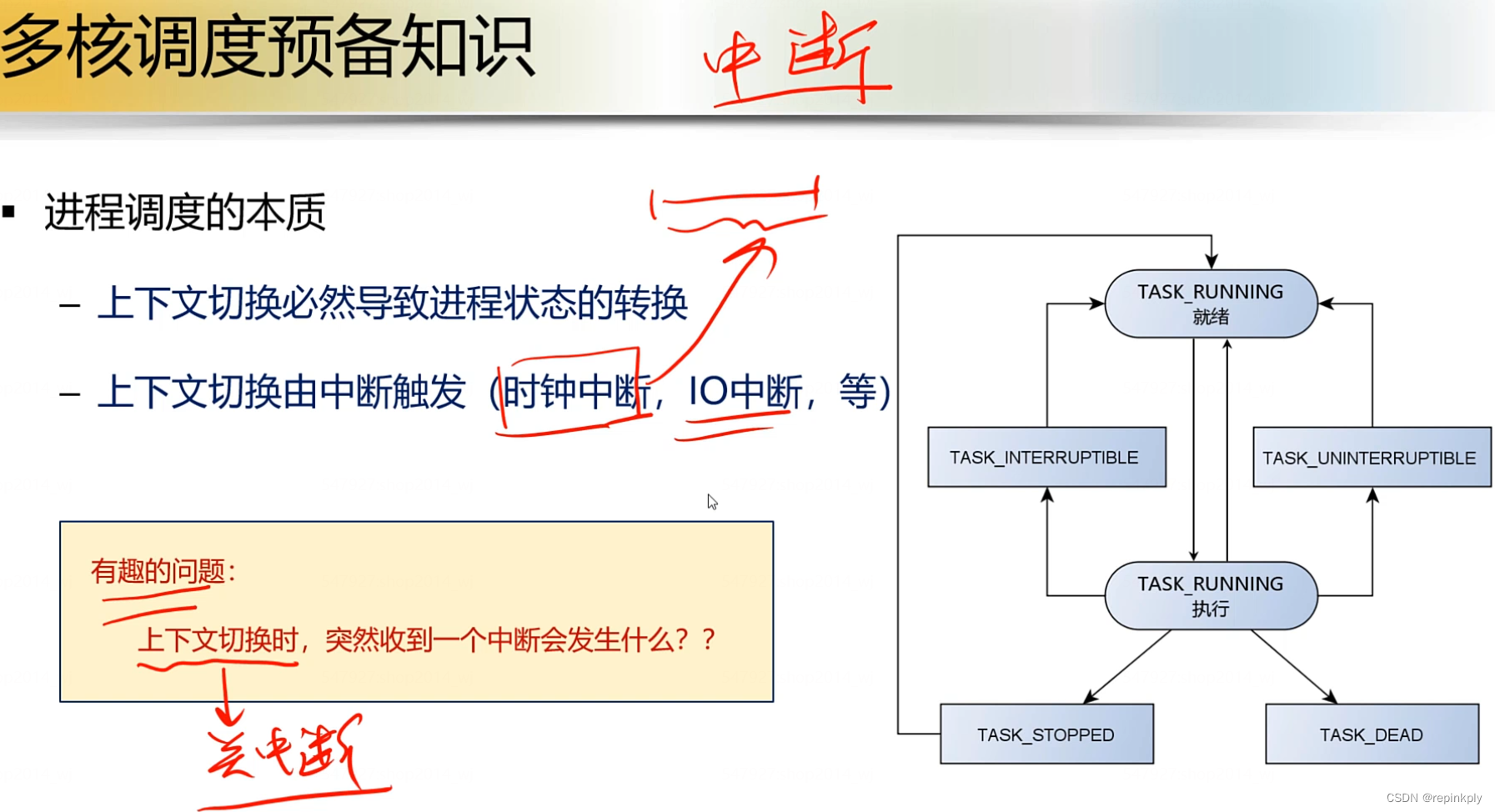
多核调度预备知识
进程调度的本质 任务/进程切换 即:上下文切换,内核对处理器上执行的进程进行切换“上下文” 指:寄存器的值“上下文切换”指: 将寄存器的值保存到内存中(进程被剥夺处理器,停止执行)将另一组寄存器的值从内存中加载到…...

什么是Git?解释Git的分布式版本控制系统的优势?
1、什么是Git?解释Git的分布式版本控制系统的优势? Git是一个开源的分布式版本控制系统,用于跟踪和管理代码库的版本历史。它允许用户在本地计算机上跟踪和管理代码库的更改,并与其他人协作开发项目。Git的分布式特性意味着它不需…...

软考高级系统架构设计师系列论文九十五:图书馆网络应用体系安全设计
软考高级系统架构设计师系列论文九十五:图书馆网络应用体系安全设计 一、网络应用体系安全设计相关知识点二、摘要三、正文四、总结一、网络应用体系安全设计相关知识点 软考高级系统架构设计师:计算机网络...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...
