多核调度预备知识
进程调度的本质
任务/进程切换
- 即:上下文切换,内核对处理器上执行的进程进行切换
- “上下文” 指:寄存器的值
- “上下文切换”指:
- 将寄存器的值保存到内存中(进程被剥夺处理器,停止执行)
- 将另一组寄存器的值从内存中加载到寄存器(调度下一个进程执行)
- 对于处理器来说,随着时间的流逝,是在不停的执行进程。
- 在微观上轮流执行不同的进程,在宏观上,我们的感觉是进程在并行执行。
- 在进程切换的时候,会发生上下文改变,上下文改变的是寄存器的值。
当时间片耗完,不管进程正在执行什么代码,都一定会发生上下文切换。
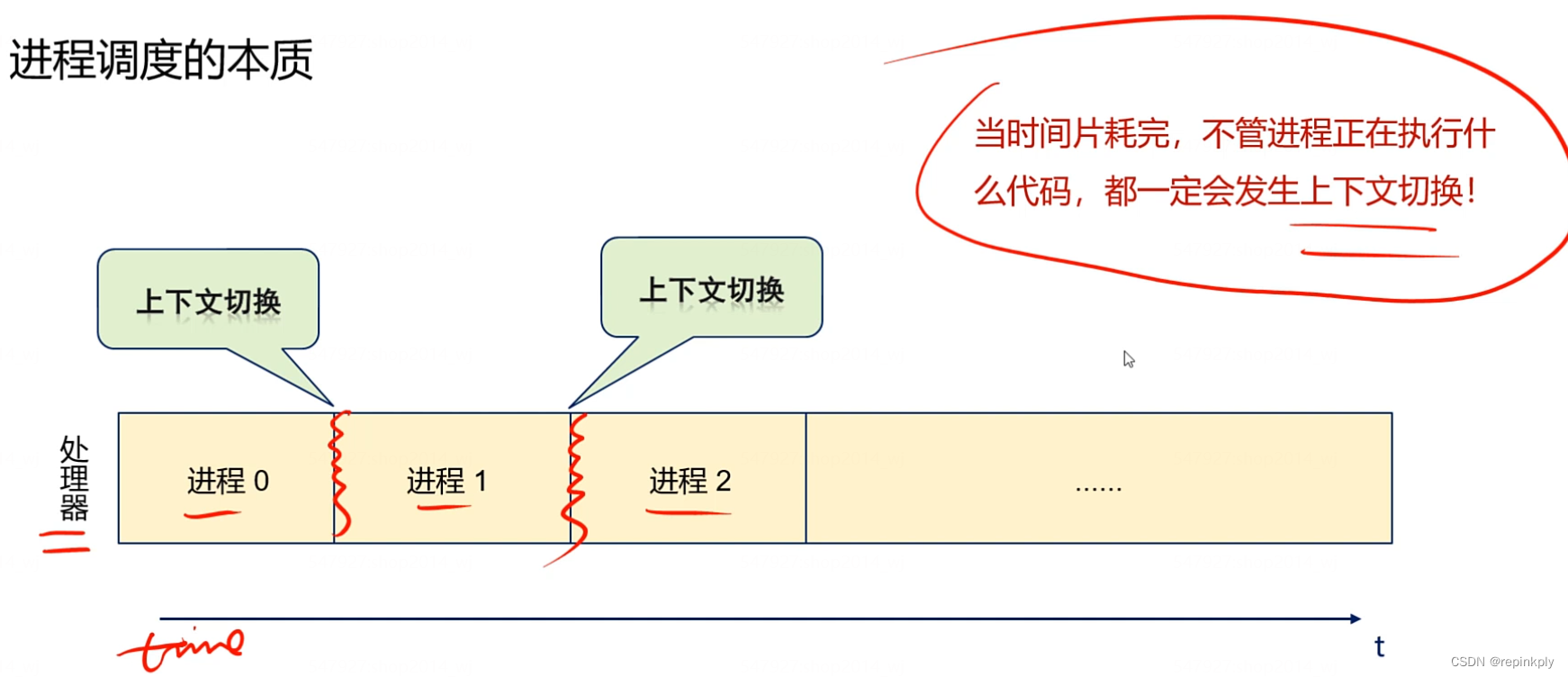
上下文切换怎么发生的?
上下文切换这件事是怎么发生的?
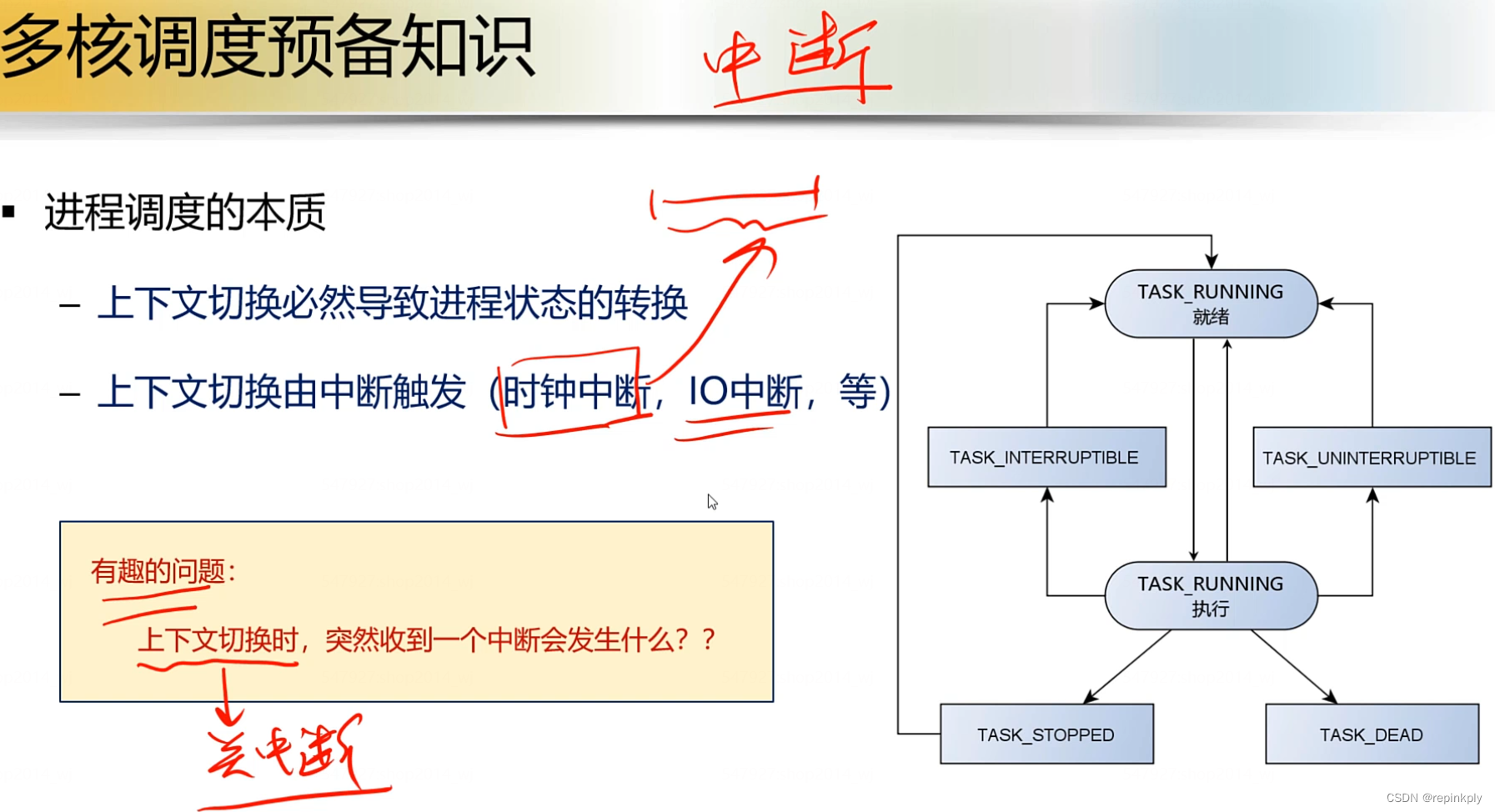
是中断触发的。对于内核来说,会不断地触发时钟中断,通过时钟中断就可以触发上下文的切换。当然,除了时钟中断之外,还有IO中断也可以触发中断。
上下文切换的时候,是运行在内核模式的,可以有权限关闭中断的。
相关文章:

多核调度预备知识
进程调度的本质 任务/进程切换 即:上下文切换,内核对处理器上执行的进程进行切换“上下文” 指:寄存器的值“上下文切换”指: 将寄存器的值保存到内存中(进程被剥夺处理器,停止执行)将另一组寄存器的值从内存中加载到…...

什么是Git?解释Git的分布式版本控制系统的优势?
1、什么是Git?解释Git的分布式版本控制系统的优势? Git是一个开源的分布式版本控制系统,用于跟踪和管理代码库的版本历史。它允许用户在本地计算机上跟踪和管理代码库的更改,并与其他人协作开发项目。Git的分布式特性意味着它不需…...

软考高级系统架构设计师系列论文九十五:图书馆网络应用体系安全设计
软考高级系统架构设计师系列论文九十五:图书馆网络应用体系安全设计 一、网络应用体系安全设计相关知识点二、摘要三、正文四、总结一、网络应用体系安全设计相关知识点 软考高级系统架构设计师:计算机网络...
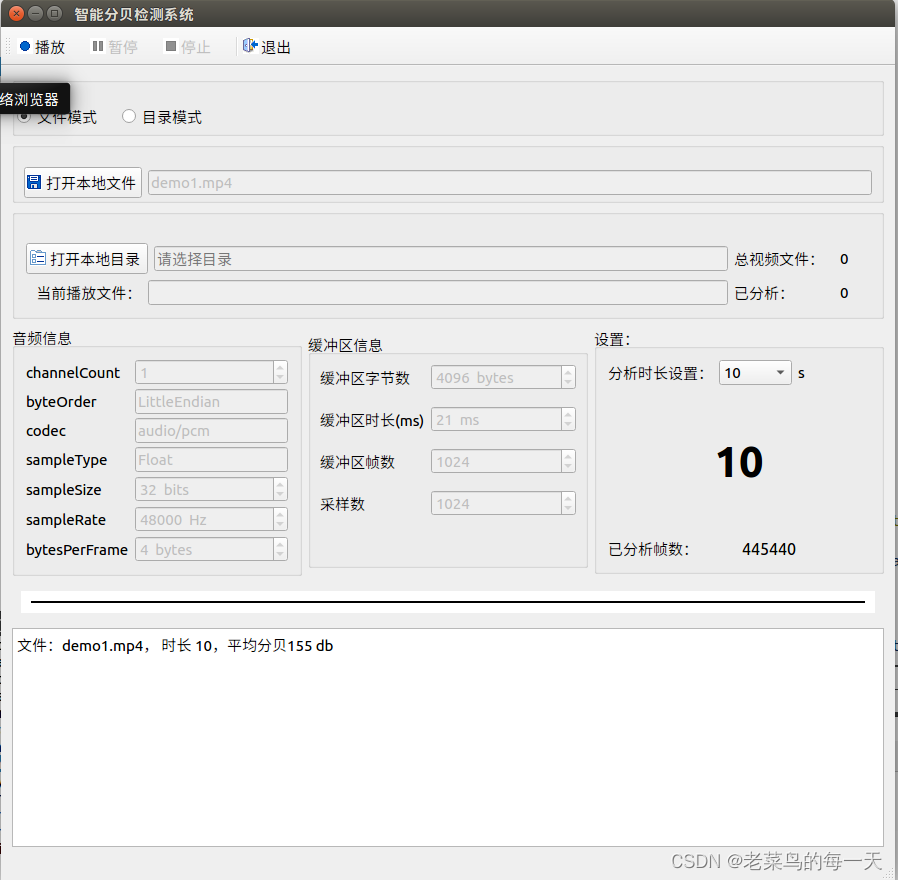
qt 实现音视频的分贝检测系统
项目场景: 目前的产品经常播放m3u8流,有的视频声音正常,有的视频声音就偏低,即使放到最大音量声音也是比较小,所以就产生了某种需求,能否自动感知视频声音的大小,如果发现声音比较小的情况&…...

SSM框架和Spring Boot+Mybatis框架的性能比较?
SSM框架和Spring BootMybatis框架的性能比较,没有一个绝对的答案,因为它们的性能受到很多因素的影响,例如项目的规模、复杂度、需求、技术栈、团队水平、测试环境、测试方法等。因此,我们不能简单地说哪个框架的性能更好ÿ…...
6个月的测试,来面试居然要18K,我一问连8K都不值
2023年7月份我入职了深圳某家创业公司,刚入职还是很兴奋的,到公司一看我傻了,公司除了我一个自动化测试,公司的测试人员就只有2个开发3个前端1个测试还有2个UI,在粗略了解公司的业务后才发现是一个从零开始的项目&…...
优美而高效:解决服务器通信问题
题目背景 在这个问题中,我们面临着一幅服务器分布图。图中的每个单元格可能有服务器(标记为1)或者没有(标记为0)。我们的任务是找出能够与至少一台其他服务器进行通信的服务器数量。 算法思路 为了解决这个问题&…...
)
C++模板的模板参数(五)
1.模板的模板参数 在C中,模板的模板参数(Template Template Parameters)是一种特殊的模板参数,允许我们将另一个模板作为模板参数传递给一个模板。这种技术可以用于实现更灵活和通用的模板设计。 模板的模板参数使用两个 “temp…...

基于jeecg-boot的flowable流程加签功能实现
更多nbcio-boot功能请看演示系统 gitee源代码地址 后端代码: https://gitee.com/nbacheng/nbcio-boot 前端代码:https://gitee.com/nbacheng/nbcio-vue.git 在线演示(包括H5) : http://122.227.135.243:9888 今天我…...
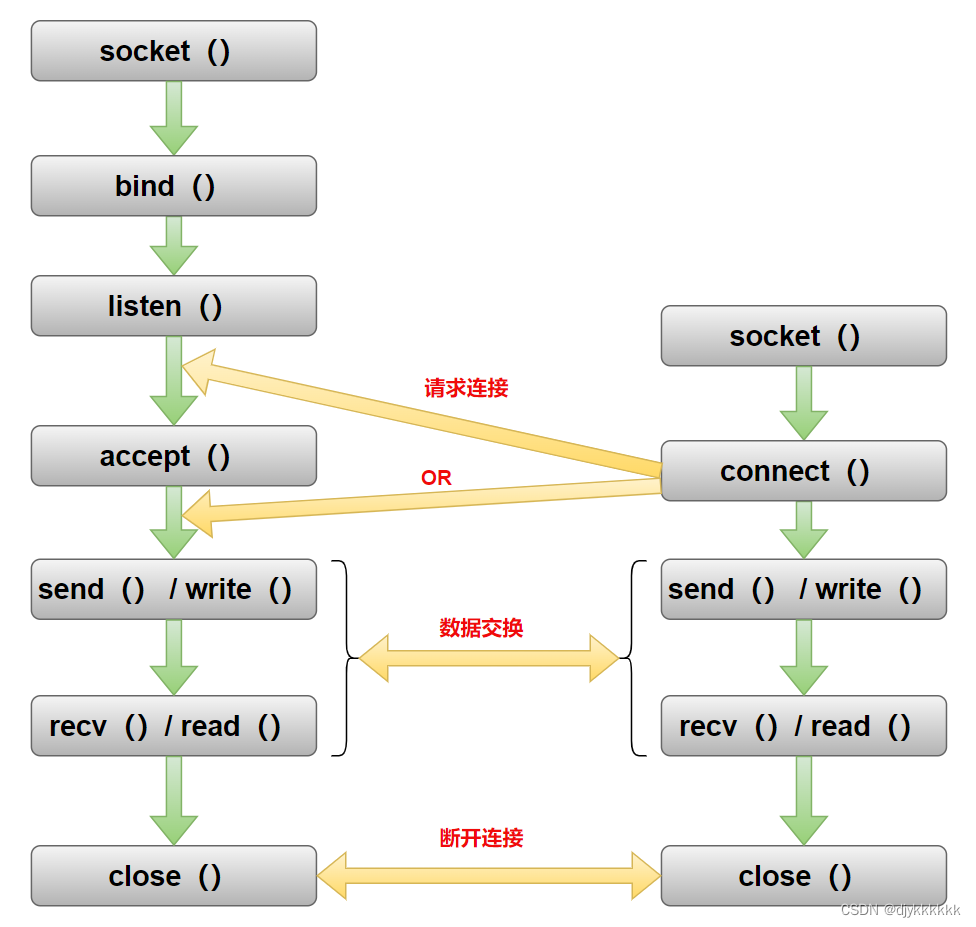
day-03 基于TCP的服务器端/客户端
一.理解TCP和UDP TCP(Transmission Control Protocol)和UDP(User Datagram Protocol)是两种常见的传输层协议,用于在计算机网络中提供可靠的数据传输。 1.TCP: 连接导向:TCP是一种面向连接的…...
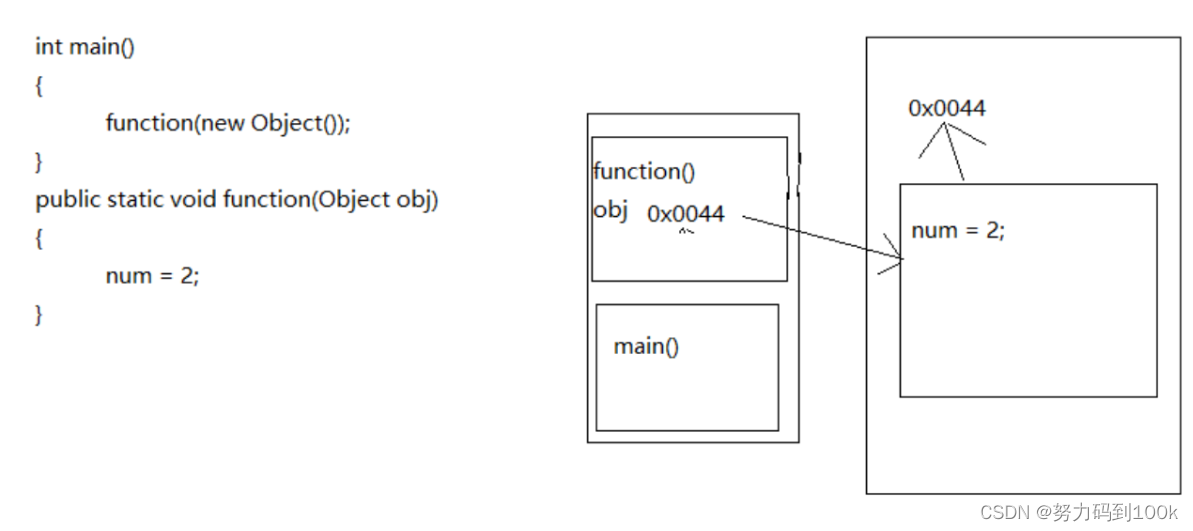
匿名对象和一般对象的区别
1.格式的不同 一般对象的格式: Object obj new Object(); 匿名对象的格式: new Object(); 2.作为参数传递机制的不同 2.1先看看一般对象的使用机制 执行步骤: 1.首先程序进入main()函数,执行Object obj,…...
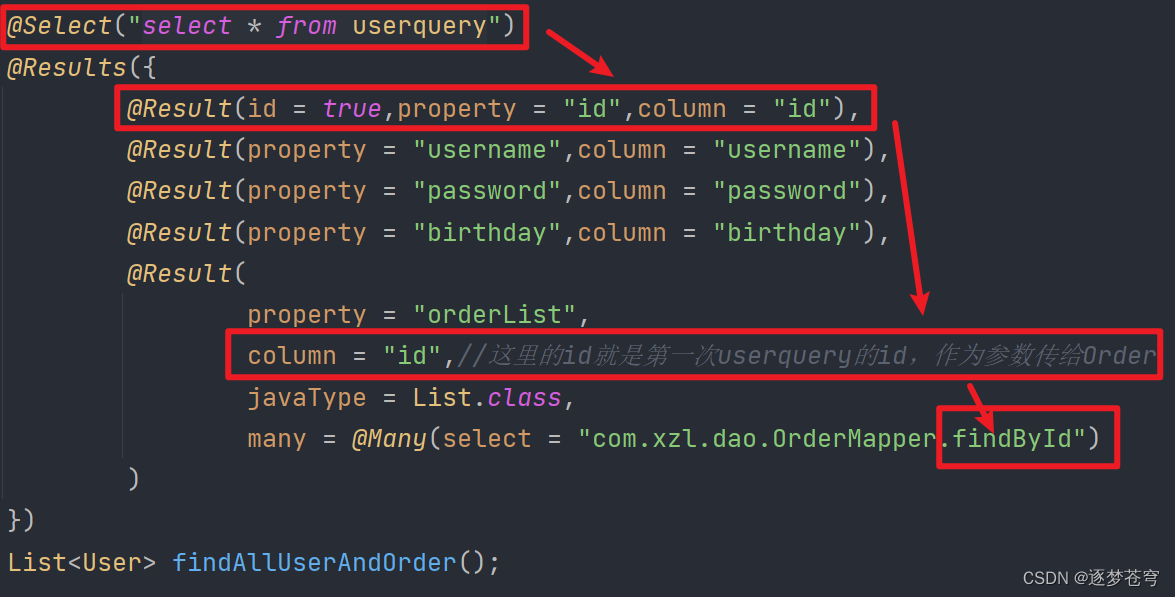
[MyBatis系列⑥]注解开发
🍃作者简介:准大三本科网络工程专业在读,持续学习Java,努力输出优质文章 ⭐MyBatis系列①:增删改查 ⭐MyBatis系列②:两种Dao开发方式 ⭐MyBatis系列③:动态SQL ⭐MyBatis系列④:核心…...

[ACL2023] Exploring Lottery Prompts for Pre-trained Language Models
Exploring Lottery Prompts for Pre-trained Language Models 文章链接 清深的工作,比较有意思的一篇。作者先给出假设,对于分类问题,在有限的语料空间内总能找到一个prompt让这个问题分类正确,作者称之为lottery prompt。为此&…...
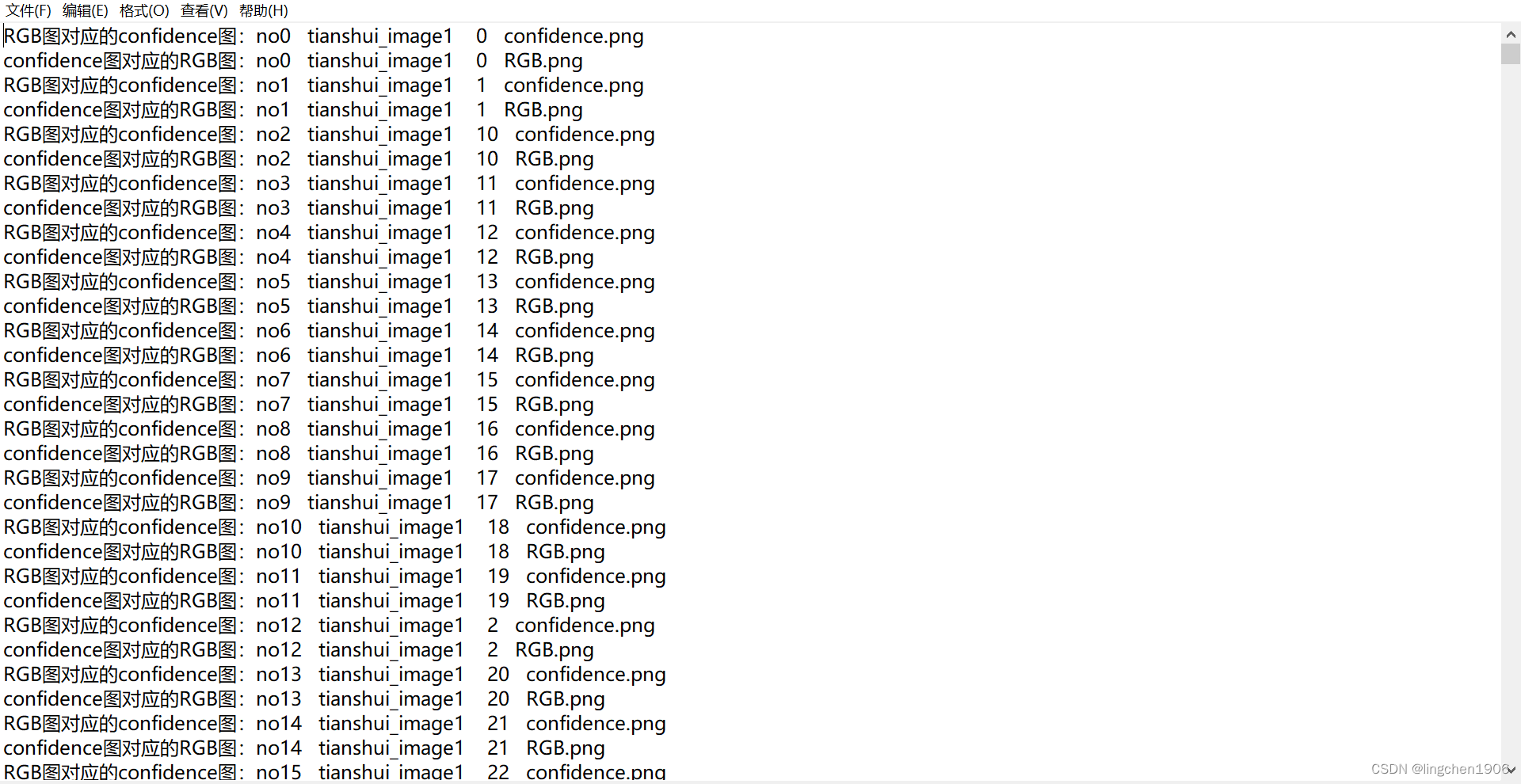
【Python编程】将同一种图片分类到同一文件夹下,并且将其分类的路径信息写成txt文件进行保存
注:数据结构同上一篇博文类似 一、代码 import os import cv2 import shutilpath0os.getcwd()\\apple\\RGB path1os.getcwd()\\apple\\tof_confidence # path2os.getcwd()\\apple\\tof_depth # path3os.getcwd()\\apple\\tof_depthRGB # path4os.getcwd()\\apple\…...

单例模式的相关知识
饿汉模式 package Thread; class Singleton{private static Singleton instance new Singleton();public static Singleton getInstance(){return instance;}private Singleton(){} }public class demo1 {public static void main(String[] args) {Singleton S1 Singleton.ge…...
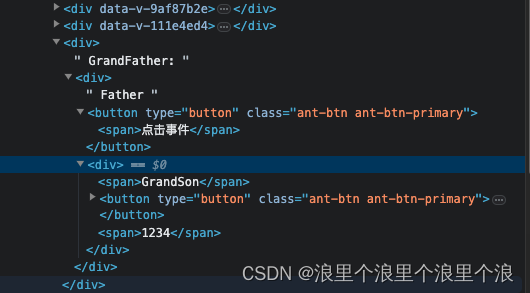
vue问题相关记录
1. vue的 nextTick的原理 首先vue实现响应式并不是数据发生变化后dom立即更新,而是按照一定的策略 异步执行dom更新的。 vue在修改数据后,试图不会立即进行更新,而是要等同一事件循环机制内所有数据变化完成之后,在统一更新 next…...

skywalking服务部署
一、前言 Apache SkyWalking 是一个开源的分布式跟踪、监控和诊断系统,旨在帮助用户监控和诊断分布式应用程序、微服务架构和云原生应用的性能和健康状况。它提供了可视化的分析工具,帮助开发人员和运维团队深入了解应用程序的性能、调用链和异常情况 …...

【uni-app】压缩图片并添加水印
总体思路 dom 结点 这里的 cvHeight 和 cvWidth 初始时要设置为你后续需要压缩后的最大宽高。假设我们在图片上传后图片最大为 350 * 350 <u-upload :fileList"baseInfoFormData.entrustFileList" afterRead"afterFileRead" multiple></u-uploa…...

《每天十分钟》-红宝书第4版-变量、作用域与内存
最近有点忙,好长时间没抄经了,今天继续,之前语言基础相对简单,跳过一部分操作符。 变量 js 的变量是特殊的松散类型,由于没有规则定义变量必须包含什么数据类型,变量的值和数据类型在脚本生命期内可以改变…...

NFTScan | 08.21~08.27 NFT 市场热点汇总
欢迎来到由 NFT 基础设施 NFTScan 出品的 NFT 生态热点事件每周汇总。周期:2023.08.21~ 2023.08.27 NFT Hot News 01/ NFT 品牌体验平台 Recur 将于 11 月 16 日彻底关闭,此前曾获 5000 万美元融资 8 月 21 日,NFT 品牌体验平台 Recur 在 X…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...
