优美而高效:解决服务器通信问题
题目背景
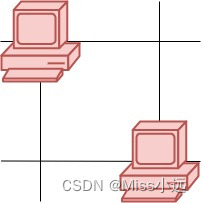
在这个问题中,我们面临着一幅服务器分布图。图中的每个单元格可能有服务器(标记为1)或者没有(标记为0)。我们的任务是找出能够与至少一台其他服务器进行通信的服务器数量。
算法思路
为了解决这个问题,我们可以采用以下两个阶段的算法思路:
第一阶段:统计与定位
在第一阶段中,我们将统计每行和每列上的服务器数量,并记录每台服务器的位置。
第二阶段:通信判断
在第二阶段,我们会逐个检查每台服务器,判断它是否能够与其他服务器进行通信。
解决问题的步骤
第一阶段:统计与定位
首先,我们将统计每行和每列的服务器数量,并记录每台服务器的位置。这将为后续的通信判断奠定基础。
// 统计每行每列的服务器数量,记录服务器位置
for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {if (grid[i][j] == 1) {rowCounts[i]++;colCounts[j]++;servers.emplace_back(i, j);}}
}
第二阶段:通信判断
在第二阶段,我们将遍历每台服务器,判断它是否能够与其他服务器进行通信。
// 遍历每台服务器,判断其通信能力
for (const auto& server : servers) {int row = server.first;int col = server.second;// 判断是否能够与其他服务器通信if (rowCounts[row] > 1 || colCounts[col] > 1) {count++;}
}
代码解析
- 首先,我们创建了两个数组
rowCounts和colCounts,用于分别统计每行和每列上的服务器数量。 - 我们使用了一个
servers向量,用于记录每台服务器的位置,以便后续的通信判断。 - 第一阶段中,我们遍历整个网格,统计每行和每列上的服务器数量,并记录服务器的位置。
- 第二阶段中,我们遍历每台服务器,判断其所在行或列上是否有其他服务器。如果有,将计数器
count增加。
知识点总结
通过解决这个问题,我们涵盖了以下知识点:
-
二维数组的遍历和元素访问。
-
向量的使用和操作,以及向量中存储自定义类型。
-
如何统计数组元素个数。
-
遍历数组,判断通信关系,实现问题求解。
总结
通过本文,我们深入探讨了如何解决服务器通信问题。我们从统计与定位以及通信判断两个阶段出发,一步步构建了解决问题的思路。通过灵活运用数组、向量和循环等基础概念,我们成功地编写出了能够高效解决问题的算法。
在解决问题的过程中,我们掌握了以下关键知识点:
-
二维数组操作: 我们学会了如何遍历二维数组,并在其中定位特定元素,以获取服务器的位置信息。
-
向量的灵活应用: 我们使用向量来存储服务器的位置,进而实现通信判断。这展示了向量在处理动态数量数据上的优势。
-
数据统计和判断: 我们通过统计每行和每列的服务器数量,实现了对服务器通信能力的判断。这种思路在解决类似问题时非常有用。
通过这个问题的解决,我们不仅锻炼了对算法和数据结构的掌握,还培养了分析问题、拆分问题以及逐步解决问题的思维能力。这些技能在日后的编程工作中将非常有用
相关文章:

优美而高效:解决服务器通信问题
题目背景 在这个问题中,我们面临着一幅服务器分布图。图中的每个单元格可能有服务器(标记为1)或者没有(标记为0)。我们的任务是找出能够与至少一台其他服务器进行通信的服务器数量。 算法思路 为了解决这个问题&…...
)
C++模板的模板参数(五)
1.模板的模板参数 在C中,模板的模板参数(Template Template Parameters)是一种特殊的模板参数,允许我们将另一个模板作为模板参数传递给一个模板。这种技术可以用于实现更灵活和通用的模板设计。 模板的模板参数使用两个 “temp…...

基于jeecg-boot的flowable流程加签功能实现
更多nbcio-boot功能请看演示系统 gitee源代码地址 后端代码: https://gitee.com/nbacheng/nbcio-boot 前端代码:https://gitee.com/nbacheng/nbcio-vue.git 在线演示(包括H5) : http://122.227.135.243:9888 今天我…...
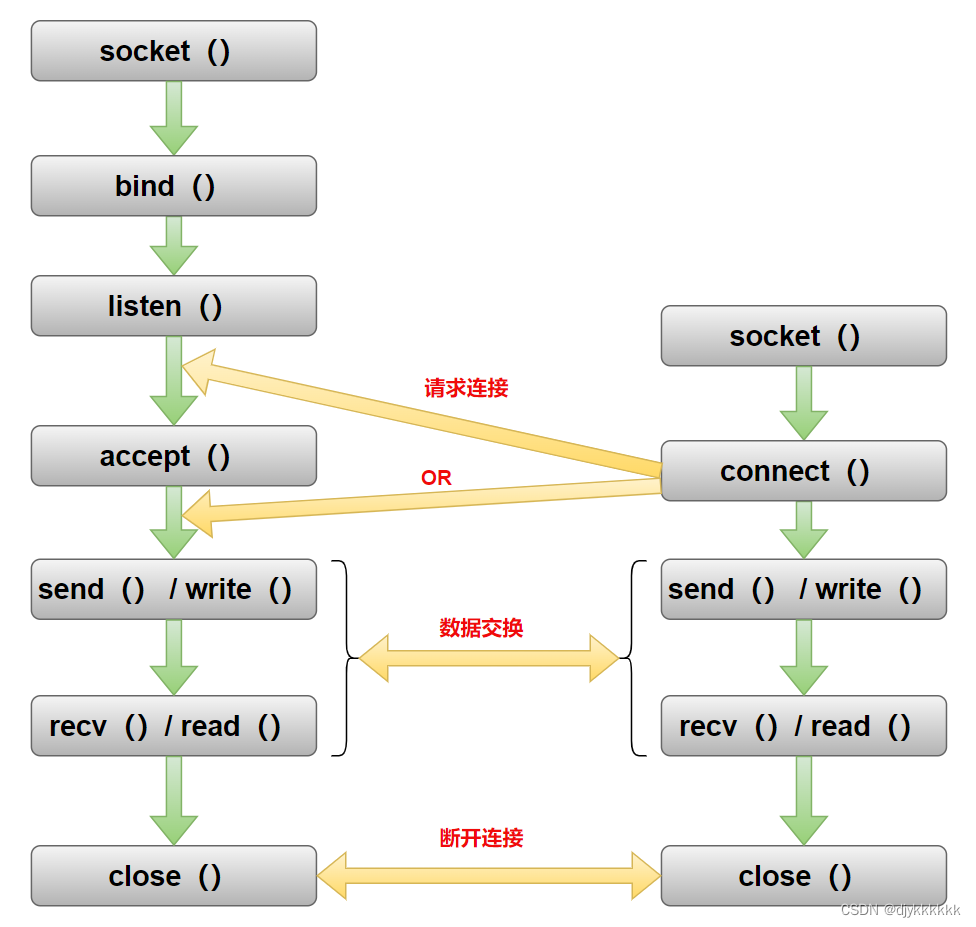
day-03 基于TCP的服务器端/客户端
一.理解TCP和UDP TCP(Transmission Control Protocol)和UDP(User Datagram Protocol)是两种常见的传输层协议,用于在计算机网络中提供可靠的数据传输。 1.TCP: 连接导向:TCP是一种面向连接的…...
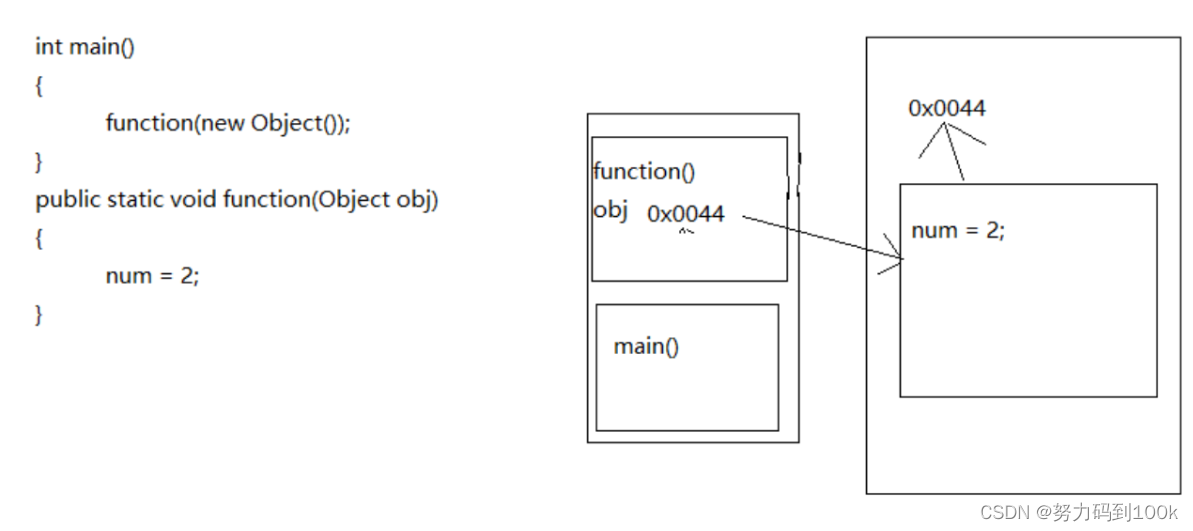
匿名对象和一般对象的区别
1.格式的不同 一般对象的格式: Object obj new Object(); 匿名对象的格式: new Object(); 2.作为参数传递机制的不同 2.1先看看一般对象的使用机制 执行步骤: 1.首先程序进入main()函数,执行Object obj,…...
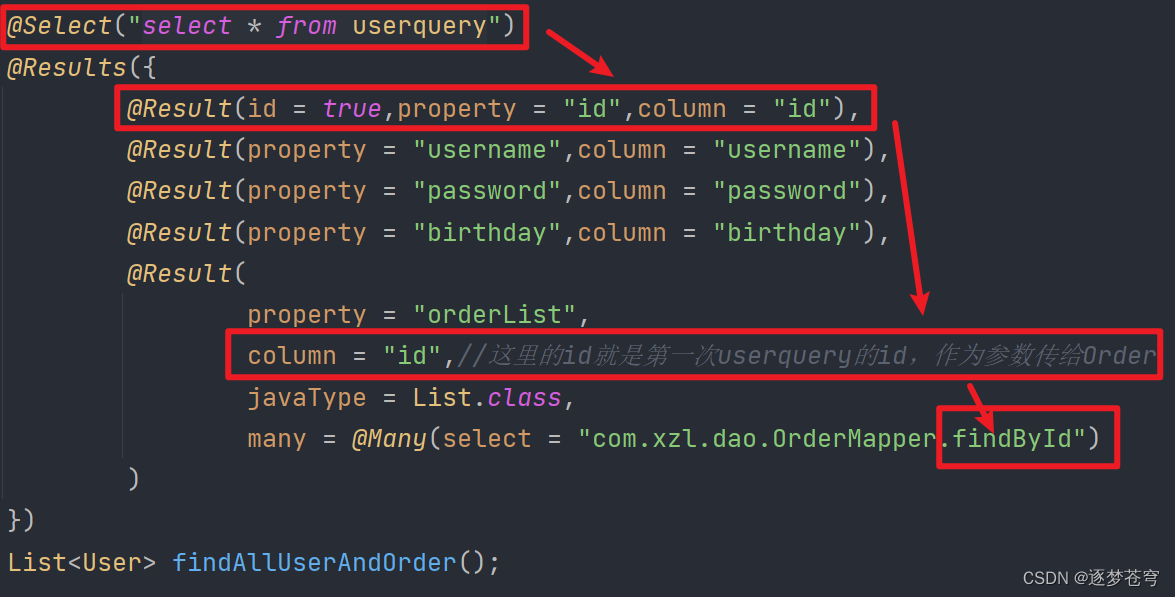
[MyBatis系列⑥]注解开发
🍃作者简介:准大三本科网络工程专业在读,持续学习Java,努力输出优质文章 ⭐MyBatis系列①:增删改查 ⭐MyBatis系列②:两种Dao开发方式 ⭐MyBatis系列③:动态SQL ⭐MyBatis系列④:核心…...

[ACL2023] Exploring Lottery Prompts for Pre-trained Language Models
Exploring Lottery Prompts for Pre-trained Language Models 文章链接 清深的工作,比较有意思的一篇。作者先给出假设,对于分类问题,在有限的语料空间内总能找到一个prompt让这个问题分类正确,作者称之为lottery prompt。为此&…...
【Python编程】将同一种图片分类到同一文件夹下,并且将其分类的路径信息写成txt文件进行保存
注:数据结构同上一篇博文类似 一、代码 import os import cv2 import shutilpath0os.getcwd()\\apple\\RGB path1os.getcwd()\\apple\\tof_confidence # path2os.getcwd()\\apple\\tof_depth # path3os.getcwd()\\apple\\tof_depthRGB # path4os.getcwd()\\apple\…...

单例模式的相关知识
饿汉模式 package Thread; class Singleton{private static Singleton instance new Singleton();public static Singleton getInstance(){return instance;}private Singleton(){} }public class demo1 {public static void main(String[] args) {Singleton S1 Singleton.ge…...
vue问题相关记录
1. vue的 nextTick的原理 首先vue实现响应式并不是数据发生变化后dom立即更新,而是按照一定的策略 异步执行dom更新的。 vue在修改数据后,试图不会立即进行更新,而是要等同一事件循环机制内所有数据变化完成之后,在统一更新 next…...

skywalking服务部署
一、前言 Apache SkyWalking 是一个开源的分布式跟踪、监控和诊断系统,旨在帮助用户监控和诊断分布式应用程序、微服务架构和云原生应用的性能和健康状况。它提供了可视化的分析工具,帮助开发人员和运维团队深入了解应用程序的性能、调用链和异常情况 …...

【uni-app】压缩图片并添加水印
总体思路 dom 结点 这里的 cvHeight 和 cvWidth 初始时要设置为你后续需要压缩后的最大宽高。假设我们在图片上传后图片最大为 350 * 350 <u-upload :fileList"baseInfoFormData.entrustFileList" afterRead"afterFileRead" multiple></u-uploa…...

《每天十分钟》-红宝书第4版-变量、作用域与内存
最近有点忙,好长时间没抄经了,今天继续,之前语言基础相对简单,跳过一部分操作符。 变量 js 的变量是特殊的松散类型,由于没有规则定义变量必须包含什么数据类型,变量的值和数据类型在脚本生命期内可以改变…...

NFTScan | 08.21~08.27 NFT 市场热点汇总
欢迎来到由 NFT 基础设施 NFTScan 出品的 NFT 生态热点事件每周汇总。周期:2023.08.21~ 2023.08.27 NFT Hot News 01/ NFT 品牌体验平台 Recur 将于 11 月 16 日彻底关闭,此前曾获 5000 万美元融资 8 月 21 日,NFT 品牌体验平台 Recur 在 X…...

【Java 中级】一文精通 Spring MVC - 数据验证(七)
👉博主介绍: 博主从事应用安全和大数据领域,有8年研发经验,5年面试官经验,Java技术专家,WEB架构师,阿里云专家博主,华为云云享专家,51CTO 专家博主 ⛪️ 个人社区&#x…...

css奇数偶数选择器
前端项目开发中,需要根据行数的奇数和偶数的不同,设置不同的颜色显示,以在视觉上给用户以良好的浏览体验,这里就需要使用css奇数偶数选择器。 主要用的::nth-of-type或者:nth-child。 方式一:nth-child div:nth-chi…...

【算法】双指针求解盛最多水的容器
Problem: 11. 盛最多水的容器 文章目录 题目解析算法原理讲解复杂度Code 题目解析 首先我们来解析一下本题 题目中说到,要找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 那我们现在来看最外侧的两根,一个高度为8&#…...
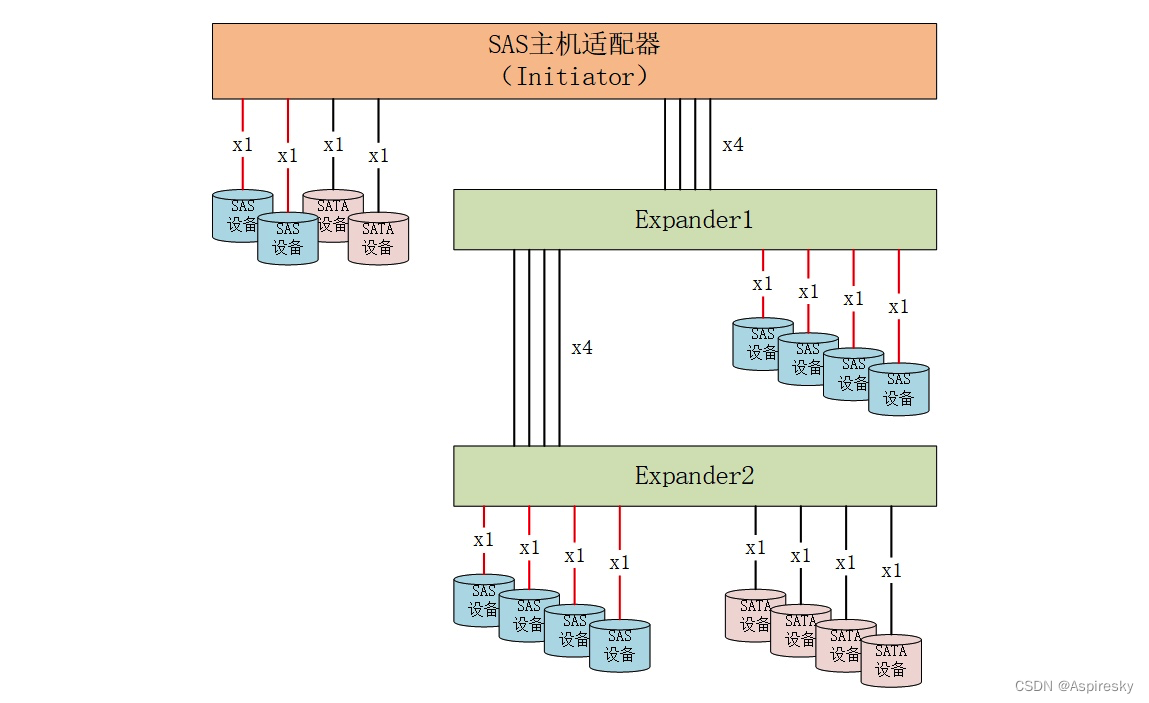
浅析SAS协议:设备接入与探测
文章目录 SAS设备初始化OOB信号SAS设备间OOB交互场景一:SAS设备两边同时发送SAS COMINIT信号场景二:SAS设备A先发送COMINIT信号场景三:SAS设备B错过COMINIT信号 SAS与SATA设备间OOB交互场景一:SATA设备未响应COMSAS信号场景二&…...

RISC-V IOPMP实际用例-Andes SoC‘s Rapid-k模型
安全之安全(security)博客目录导读 2023 RISC-V中国峰会 安全相关议题汇总 说明:本文参考RISC-V 2023中国峰会如下议题,版权归原作者所有。...

【高阶数据结构】哈希表详解
文章目录 前言1. 哈希的概念2. 哈希冲突3. 哈希函数3.1 直接定址法3.2 除留余数法--(常用)3.3 平方取中法--(了解)3.4 折叠法--(了解)3.5 随机数法--(了解)3.6 数学分析法--(了解) 4. 哈希冲突的解决方法及不同方法对应的哈希表实现4.1 闭散列(开放定址法࿰…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

ubuntu中安装conda的后遗症
缘由: 在编译rk3588的sdk时,遇到编译buildroot失败,提示如下: 提示缺失expect,但是实测相关工具是在的,如下显示: 然后查找借助各个ai工具,重新安装相关的工具,依然无解。 解决&am…...
