图神经网络与分子表征:番外——基组选择
学过高斯软件的人都知道,我们在撰写输入文件 gjf 时需要准备输入【泛函】和【基组】这两个关键词。
【泛函】敲定计算方法,【基组】则类似格点积分中的密度,与计算精度密切相关。
部分研究人员借用高斯中的一系列基组去包装输入几何信息(距离、角度和二面角),这样做一方面提高了GNN的可解释性,另一方面也实实在在的提高了模型精度。从 AI 角度看,embedding则可以看作是几何信息的升维。
具体来说:
- 如果模型输入仅有距离信息,则采用径向基函数去embedding。常用的有 Gaussian ,也有Bessel
- 如果模型输入含有距离和角度信息。在直角坐标系下,可以用 Gaussian 和 sin 函数组embedding。在球坐标系下,可以考虑 spherical Bessel functions and spherical harmonics 组合。其中 spherical harmonics 采用m=0的形式。
- 如果模型输入含有距离,角度和二面角信息,一般采用 spherical Bessel functions and spherical harmonics 组合。可能有其他的,但目前涉及二面角的模型较少,据我了解,Spherenet和ComENet均采用的是这种组合。
下面进行简要介绍:
Gaussian 系列基组
SchNet网络架构中使用的基组,是目前用途最广的基组之一。
我们借助 DIG 框架中 schnet 的实现,对其进行可视化:
from dig.threedgraph.method.schnet.schnet import *import numpy as np
import math
import matplotlib.pyplot as pltimport torchdist_test = torch.arange(0.01, 5.01, 0.01)
dist_emb = emb(num_gaussians=5)
y = dist_emb(dist_test)
y = y.Tfor idx, y_plot in enumerate(y):x = [a_dist.detach().numpy() for a_dist in dist_test]y = [an_emb.detach().numpy() for an_emb in y_plot]plt.plot(x, y, label=f"Gaussian embedding {idx}")plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()
结果如下图所示:
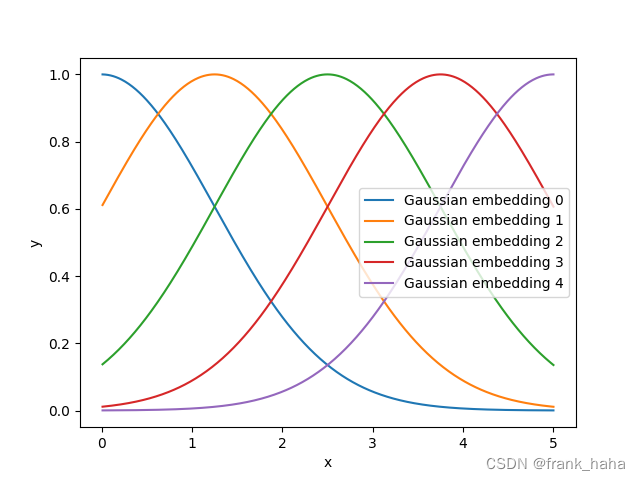
所谓,“对几何信息进行嵌入”,指,同一个距离信息对应x轴一个点。如果高斯基组有5,则,嵌入后,该距离信息就映射到了5个口袋里,获得一组长度为5的特征向量。
此处为了清晰的可视化,仅设置 num_gaussians=5 ,在实际应用中,这一数值往往设的很高。例如,原版的 schnet 将这一数值设为 300,在 DIG 版本中,这一数值是默认的 50,而在最新的 schnetpack 中,这一数值 降为了 20.
Bessel 系列基组
与高斯基组类似,Bessel 系列基组用于 embedding 距离信息,文献里用 spherical Bessel functions 表示。
其源头可以追溯到微分方程的求解,spherical Bessel functions 是作为一系列解中的径向部分存在,也常被称为 radical Bessel functions。
最早使用 Bessel functions 的(可能不严谨)GNN大概是 DimeNet。据 DimeNet 原文报道,使用 Bessel functions 会带来一定程度的精度提升。
我们借助 DIG 框架中 DimeNet 的实现,对其进行可视化:
from dig.threedgraph.method.spherenet.features import *import numpy as np
import math
import matplotlib.pyplot as pltimport torchdist_test = torch.arange(0.01, 5.01, 0.01)
dist_emb = dist_emb(num_radial=5)
y = dist_emb(dist_test)
y = y.Tfor idx, y_plot in enumerate(y):x = [a_dist.detach().numpy() for a_dist in dist_test]y = [an_emb.detach().numpy() for an_emb in y_plot]plt.plot(x, y, label=f"radical_basis_{idx}")plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()
结果如下图所示:
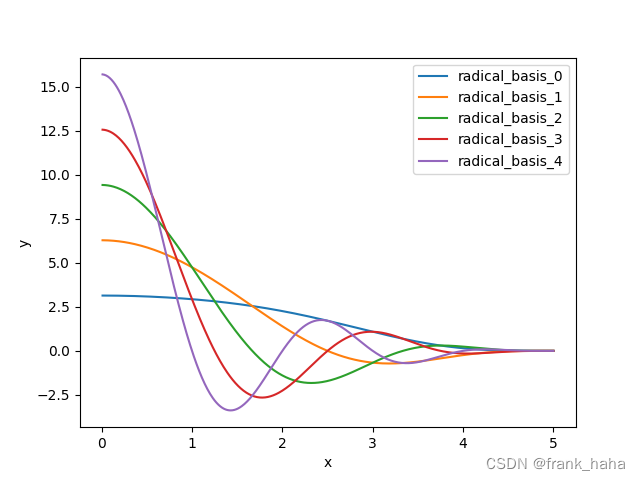
spherical harmonics 基组
spherical Bessel functions 和 spherical harmonics 不是一个基组。他俩分别对应方程特解中的径向和角度部分。
(下图为 ComENet 中的概述)
spherical harmonics 基组常常在球极坐标系下,和 spherical Bessel functions 配套使用。
如果输入的几何信息仅有角度,没有二面角,我们将 spherical harmonics 中的 m 置零。
此时得到的是一系列二维的 embedding 矩阵。
我们借助 DIG 框架中 SphereNet 的实现,对其进行可视化(源码稍微改了改,此处仅是一些思路):
from dig.threedgraph.method.spherenet.features import *import numpy as np
import math
import matplotlib.pyplot as pltimport torchangle_emb = angle_emb(num_spherical=4, num_radial=4, cutoff=4)
rlist = np.arange(0, 4.01, 0.005) # Angstroms
thetalist = np.radians(np.arange(0, 361, 0.5)) # Radians
rmesh, thetamesh = np.meshgrid(rlist, thetalist) # Generate a meshn = 1
l = 1
fig = plt.figure()
info = angle_emb(torch.tensor(rlist), torch.tensor(thetalist))
info_0 = info[n, l]
info_0 = info_0.detach().numpy()info_0 = info_0.reshape(len(rlist), len(thetalist))
info_0 = info_0.T
fig, ax = plt.subplots(subplot_kw=dict(projection='polar'))
ax.contourf(thetamesh, rmesh, info_0, 100, cmap='RdBu')
ax.set_rticks([])
ax.set_xticks([])
plt.savefig(f'./basis/n_{n}_l_{l}.png', dpi=400)
结果如下图所示:
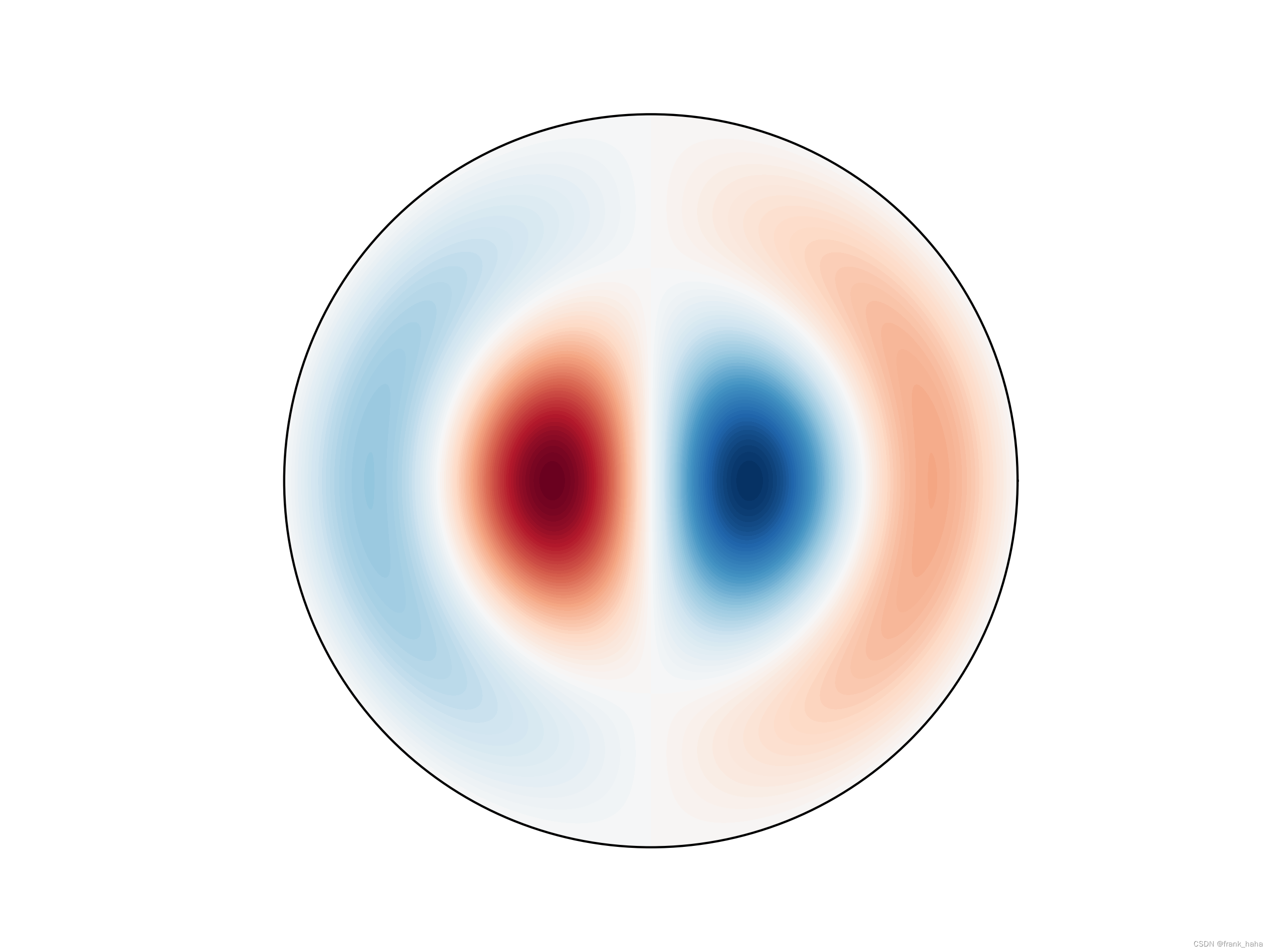
我们可以得到一系列能够embedding角度和距离信息的函数。
下图是DimeNet原文中的图:
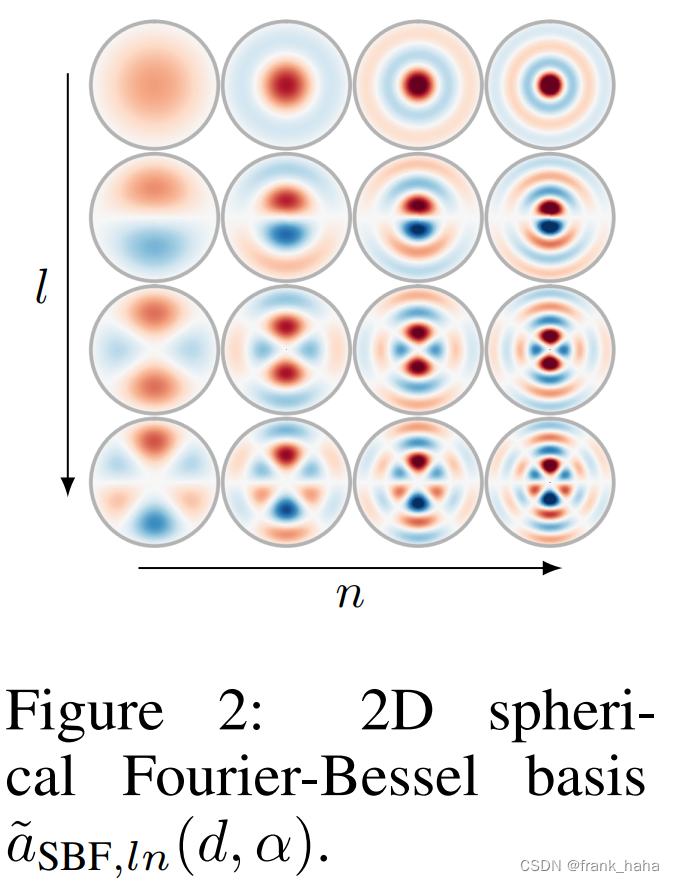
需要注意的是,DimeNet源码中对 l=0 的径向函数进行了修改,所以无法复现 Figure 2 第一行。
我们还可以借助 scipy 进行实现,例如,下面我们对角度部分 ( spherical harmonics )进行可视化(不涉及径向部分,径向部分在 scipy.special._spherical_bessel 里):
- 借用plotly实现可交互的可视化
import plotly.graph_objects as go
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from scipy.special import sph_harm# from scipy.special._spherical_bessel import# l, m = 3, 0for l in range(0, 4):for m in range(-l, l+1):theta = np.linspace(0, np.pi, 100)phi = np.linspace(0, 2 * np.pi, 100)theta, phi = np.meshgrid(theta, phi)xyz = np.array([np.sin(theta) * np.sin(phi),np.sin(theta) * np.cos(phi),np.cos(theta)])Y = sph_harm(abs(m), l, phi, theta)if m < 0:Y = np.sqrt(2) * (-1) ** m * Y.imagelif m > 0:Y = np.sqrt(2) * (-1) ** m * Y.realYx, Yy, Yz = np.abs(Y) * xyzfig = go.Figure(data=[go.Surface(x=Yx, y=Yy, z=Yz, surfacecolor=Y.real), ])fig.update_layout(title=f'Y_l_{l}_m_{m}', )fig.write_html(rf'./pics_html/Y_l_{l}_m_{m}.html')- 借用matplotlib实现静态的可视化:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
# The following import configures Matplotlib for 3D plotting.
from mpl_toolkits.mplot3d import Axes3D
from scipy.special import sph_harm# plt.rc('text', usetex=True)# Grids of polar and azimuthal angles
theta = np.linspace(0, np.pi, 100)
phi = np.linspace(0, 2*np.pi, 100)
# Create a 2-D meshgrid of (theta, phi) angles.
theta, phi = np.meshgrid(theta, phi)
# Calculate the Cartesian coordinates of each point in the mesh.
xyz = np.array([np.sin(theta) * np.sin(phi),np.sin(theta) * np.cos(phi),np.cos(theta)])def plot_Y(ax, el, m):"""Plot the spherical harmonic of degree el and order m on Axes ax."""# NB In SciPy's sph_harm function the azimuthal coordinate, theta,# comes before the polar coordinate, phi.Y = sph_harm(abs(m), el, phi, theta)# Linear combination of Y_l,m and Y_l,-m to create the real form.if m < 0:Y = np.sqrt(2) * (-1)**m * Y.imagelif m > 0:Y = np.sqrt(2) * (-1)**m * Y.realYx, Yy, Yz = np.abs(Y) * xyz# Colour the plotted surface according to the sign of Y.cmap = plt.cm.ScalarMappable(cmap='RdBu')cmap.set_clim(-0.5, 0.5)ax.plot_surface(Yx, Yy, Yz,facecolors=cmap.to_rgba(Y.real),rstride=2, cstride=2)# Draw a set of x, y, z axes for reference.ax_lim = 0.5ax.plot([-ax_lim, ax_lim], [0,0], [0,0], c='0.5', lw=1, zorder=10)ax.plot([0,0], [-ax_lim, ax_lim], [0,0], c='0.5', lw=1, zorder=10)ax.plot([0,0], [0,0], [-ax_lim, ax_lim], c='0.5', lw=1, zorder=10)# Set the Axes limits and title, turn off the Axes frame.# ax.set_title(r'$Y_{{{},{}}}$'.format(el, m))ax.set_title('Y_l_{}_m_{}'.format(el, m))ax_lim = 0.5ax.set_xlim(-ax_lim, ax_lim)ax.set_ylim(-ax_lim, ax_lim)ax.set_zlim(-ax_lim, ax_lim)ax.axis('off')# fig = plt.figure(figsize=plt.figaspect(1.))for l in range(0, 4):for m in range(-l, l+1):fig = plt.figure()ax = fig.add_subplot(projection='3d')plot_Y(ax, l, m)plt.savefig('./pics_png/Y_l_{}_m_{}.png'.format(l, m))
静态效果如下:
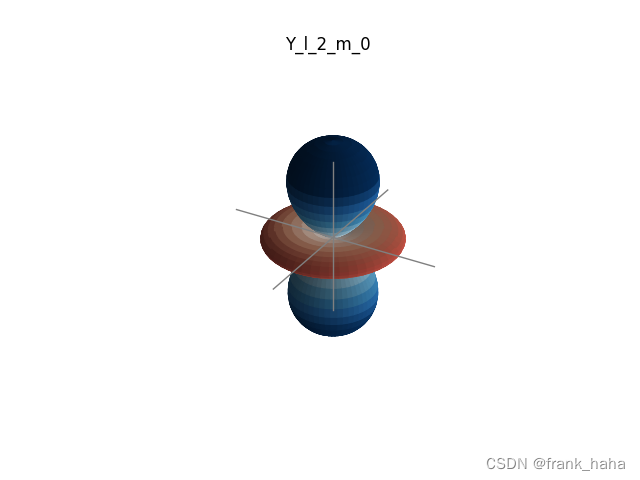
OK,至此,GNN中常用的基组(至少我所了解到的)介绍完了。
一般来说,仅涉及距离信息的架构常常采用 gaussian 基组。
如果要用 spherical harmonics 这种涉及角度的基组,一般需要将几何坐标转到球极坐标下,而这将导致网络适应等变架构时遇到困难。
当然,还有使用 tensor field 做基组的,这块我还了解的少,但看起来好像也是套的 spherical harmonics 。
相关文章:

图神经网络与分子表征:番外——基组选择
学过高斯软件的人都知道,我们在撰写输入文件 gjf 时需要准备输入【泛函】和【基组】这两个关键词。 【泛函】敲定计算方法,【基组】则类似格点积分中的密度,与计算精度密切相关。 部分研究人员借用高斯中的一系列基组去包装输入几何信息&am…...

rabbitmq笔记-rabbitmq客户端开发使用
连接RabbitMQ 1.创建ConnectionFactory,给定参数ip地址,端口号,用户名和密码等 2.创建ConnectionFactory,使用uri方式实现,创建channel。 注意: Connection可以用来创建多个channel实例,但c…...
与nvl2()函数详解)
13.Oracle中nvl()与nvl2()函数详解
Oracle中nvl()与nvl2()函数详解: 函数nvl(expression1,expression2)根据参数1是否为null返回参数1或参数2的值; 函数nvl2(expression1,expression2,expression3)根据参数1是否为null返回参数2或参数3的值 1.nvl:根据参数1是否为null返回参数…...

设置某行被选中并滚动到改行
<el-table :data"tableDamItem" ref"singleTable" stripe style"width: 100%" height"250" highlight-current-row v-on:row-click"handleTableRow"></el-table>/*** 设置表格行被选中,并滚动到该行* param po…...

React钩子函数之useRef的基本使用
React钩子函数中的useRef是一个非常有用的工具,它可以用来获取DOM元素或者保存一些变量。在这篇文章中,我们将会讨论useRef的基本使用。 首先,我们需要知道useRef是如何工作的。它返回一个可变的ref对象,这个对象可以在组件的整个…...

无风扇迷你电脑信息与购买指南
本文将解释什么是无风扇迷你电脑,以及计算产品组合中你可以购买的一些不同的无风扇迷你电脑的信息指南。 无风扇迷你电脑是一种小型工业计算机,旨在处理复杂的工业工作负载。迷你电脑是通过散热器被动冷却可在各种类型的易失性环境中部署。无风扇微型计…...

比特币是怎么回事?
比特币是怎么回事? 一句话描述就是,初始化几个比特币,申请成为矿工组织,发生交易时抢单记账成功可以比特币奖励,随着比特币数量的增加,奖励越来越少。怎么记账成功呢,通过交易信息幸运数字哈希…...
vue3+ts+uniapp小程序端自定义日期选择器基于内置组件picker-view + 扩展组件 Popup 实现自定义日期选择及其他选择
vue3ts 基于内置组件picker-view 扩展组件 Popup 实现自定义日期选择及其他选择 vue3tsuniapp小程序端自定义日期选择器 1.先上效果图2.代码展示2.1 组件2.2 公共方法处理日期2.3 使用组件 3.注意事项3.1refSelectDialog3.1 backgroundColor"#fff" 圆角问题 自我记…...

Java进阶篇--泛型
前言 Java 泛型(generics)是 JDK 5 中引入的一个新特性, 泛型提供了编译时类型安全检测机制,该机制允许程序员在编译时检测到非法的类型。它允许在定义类、接口和方法时使用类型参数。这种技术使得在编译期间可以使用任何类型,而…...
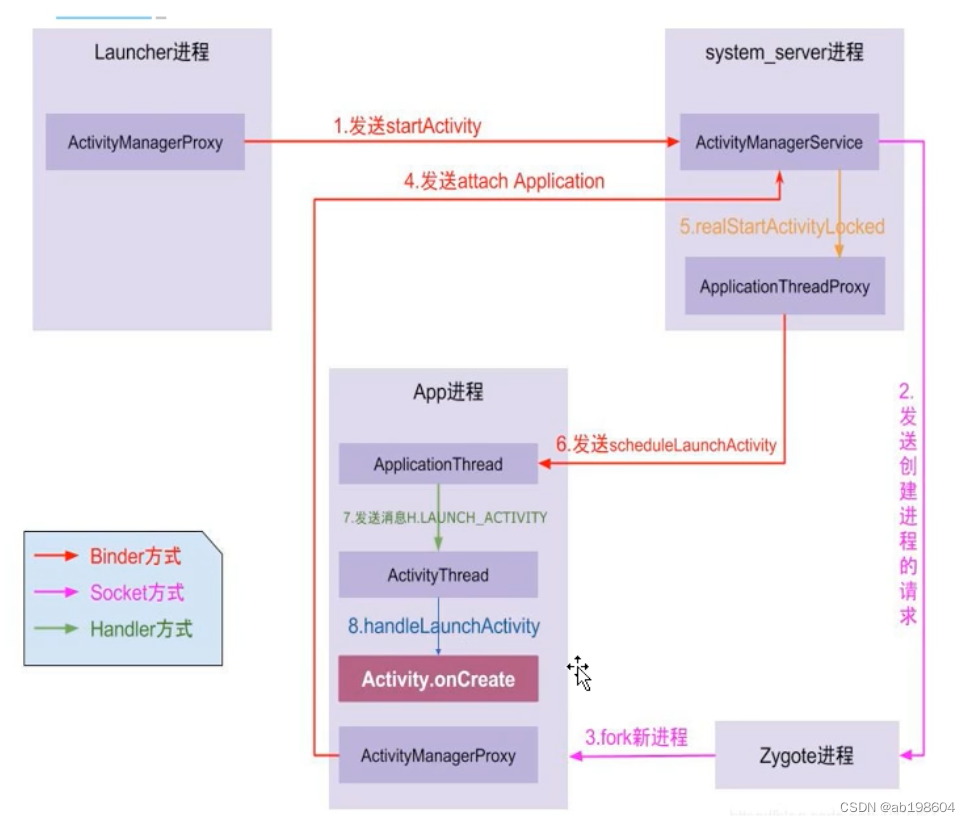
android framework之Applicataion启动流程分析
Application启动流程分析 启动方式一:通过Launcher启动app 启动方式二:在某一个app里启动第二个app的Activity. 以上两种方式均可触发app进程的启动。但无论哪种方式,最终通过通过调用AMS的startActivity()来启动application的。 根据上图…...

Linux Day10 ---Mybash
目录 一、Mybash介绍 1.1.mybash.c 打印函数 分割函数 命令函数 二、Mybash实现 2.1.打印函数 2.1.1需要使用到的功能函数 1.获取与当前用户关联的UID 2.获取与当前用户的相关信息---一个结构体(passwd) 3.获取主机信息 4.获取当前所处位置 5.给…...

Flask-Sockets和Flask-Login联合实现websocket的登录认证功能
flask_login 提供了一个方便的方式来管理用户会话。当你在 Flask 的 HTTP 视图中使用它时,你可以简单地使用 login_required 装饰器来确保用户已登录。 但是,flask_sockets 并没有直接与 flask_login 集成。如果你想在建立 WebSocket 连接时检查用户是否…...
东盟全面覆盖?长城战略部署核心区域市场,首个百万粉丝国产品牌
根据最新消息,长城汽车在东南亚地区取得了巨大的成功,成功进军了亚洲最大的汽车市场之一-印度尼西亚。这标志着长城汽车已经实现了东盟核心市场的全面覆盖,成为全球布局的重要一步。 在过去的几年里,长城汽车在东盟地区的市场布局…...
基于PHP的电脑商城系统
有需要请加文章底部Q哦 可远程调试 基于PHP的电脑商城系统 一 介绍 此电脑商城系统基于原生PHP开发,数据库mysql,前端bootstrap。用户可注册登录,购物下单,评论等。管理员登录后台对电脑商品,用户,订单&a…...

无客户端网络准入方案,为集成电路企业终端管理开启省事更省心模式
宁盾无客户端网络准入控制方案正在成为先进制造、高科技互联网企业等创新型客户的优选方案。创新型客户以技术密集型、研发人员占比高著称,在进行网络准入建设时,如何平衡好用户体验与顺利达成项目预期之间的矛盾,是创新企业 IT 安全团队格外…...

5G与4G的RRC协议之异同
什么是无线资源控制(RRC)? 我们知道,在移动通信中,无线资源管理是非常重要的一个环节,首先介绍一下什么是无线资源控制(RRC)。 手机和网络通过无线信道相互通信,彼此交…...

横扫“盲区”、“看透”缺陷,维视智造推出短波红外相机
在可见光领域,工业相机的视觉应用已经十分成熟,但在日常的客户咨询中,我们也经常接到一些“超纲需求”——客户想要检测“白底上的白色缺陷”、“不透明包装内的透明物体有无”等,均属于可见光无法实现的检测,而市面上…...

cgo踩坑:交叉编译过程出现的问题could not determine kind of name for C.XXX
尝试了网上的几种解决方法,都不行,现总结起来: 确认 /* #include <stdio.h> */ import "C"不要有空行 确认你引用的头文件存在(stdio.h这种编译器自带的不需要你确认) 如果引用了多个包,…...
技术的例子)
自然语言处理(NLP)技术的例子
以下是几个自然语言处理(NLP)技术的例子: 机器翻译:机器翻译是将一种自然语言的文本转换成另一种语言的文本的过程。这种技术应用于在线翻译器、多语言聊天机器人、多语言搜索引擎等地方。 文本分类:文本分类将文本分…...
Python“牵手”义乌购商品列表数据,关键词搜索义乌购API接口数据,义乌购API接口申请指南
义乌购平台API接口是为开发电商类应用程序而设计的一套完整的、跨浏览器、跨平台的接口规范,义乌购API接口是指通过编程的方式,让开发者能够通过HTTP协议直接访问义乌购平台的数据,包括商品信息、店铺信息、物流信息等,从而实现义…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
