Python机器学习入门笔记(3)—— 线性回归
目录
线性回归
算法简述
LinearRegression() API
SGDRegressor API
LinearRegression() 和 SGDRegressor对比
过拟合与欠拟合
岭回归
应用场景
线性回归
算法简述
线性回归是一种基本的机器学习算法,它用于建立自变量和因变量之间的线性关系模型。它假设自变量和因变量之间存在线性关系,通过最小化误差平方和来找到最优的模型参数,包括截距和斜率,以使模型的预测值尽可能地接近真实值。在实际应用中,线性回归算法广泛用于预测房价、股票价格、销售量等连续性数值型数据的预测问题。
LinearRegression() API
LinearRegression() 是一个基于最小二乘法的线性回归模型。它通过拟合一个线性方程来预测响应变量(因变量)和一个或多个解释变量(自变量)之间的关系。
LinearRegression() 可以通过一些参数进行调整来优化模型的性能,以下是其中一些常见的参数:
- fit_intercept:是否计算截距。默认为 True。
- normalize:是否对解释变量进行归一化。默认为 False。
- copy_X:是否复制解释变量。默认为 True。
- n_jobs:并行处理的数量。默认为 1。
- positive:是否强制回归系数为正。默认为 False。
在实践中,一般使用默认参数即可,只有在特定的情况下,如当数据集非常大或者具有特定的特征时,才需要进行调整。
from sklearn.linear_model import LinearRegression from sklearn.datasets import load_diabetes from sklearn.model_selection import train_test_split from sklearn.metrics import mean_squared_error# 加载糖尿病数据集 diabetes = load_diabetes()# 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, test_size=0.2, random_state=42)# 创建线性回归模型 model = LinearRegression()# 训练模型 model.fit(X_train, y_train)# 预测结果 y_pred = model.predict(X_test)# 计算均方误差 mse = mean_squared_error(y_test, y_pred) print("均方误差:", mse)在这个例子中,我们首先加载了糖尿病数据集,然后使用
train_test_split函数将数据集划分为训练集和测试集。接着,我们创建了一个线性回归模型,并使用训练集对模型进行训练。最后,我们使用测试集对模型进行测试,并计算出模型的均方误差。需要注意的是,线性回归模型的性能很大程度上依赖于特征的选择和数据的预处理。在实际应用中,我们通常会对特征进行筛选和处理,以提高模型的预测准确性。
SGDRegressor API
SGDRegressor 是一种基于随机梯度下降法的线性回归模型。相较于传统的最小二乘法,它在大规模数据集下具有更好的计算效率和泛化性能。SGDRegressor 通过随机梯度下降算法来逐步调整回归系数,从而拟合数据集。它可以用于线性回归、L1正则化回归(Lasso)、L2正则化回归(Ridge)以及弹性网络回归(Elastic Net)等。
SGDRegressor 可以通过一些参数进行调整来优化模型的性能,以下是其中一些常见的参数:
- loss:损失函数类型。默认为 'squared_loss',即使用平方误差作为损失函数。也可以选择 'huber'、'epsilon_insensitive' 或 'squared_epsilon_insensitive'。
- penalty:正则化类型。默认为 'l2',即L2正则化。也可以选择 'l1' 或 'elasticnet'。
- alpha:正则化强度。默认为 0.0001。
- l1_ratio:当 penalty='elasticnet' 时,L1正则化的比例。默认为 0.15。
- fit_intercept:是否计算截距。默认为 True。
- learning_rate:学习率类型。默认为 'invscaling',即随时间递减的学习率。也可以选择 'constant' 或 'optimal'。
- eta0:学习率的初始值。默认为 0.01。
- power_t:学习率的递减速率。默认为 0.25。
- early_stopping:是否启用提前停止。默认为 False。
- validation_fraction:提前停止时验证集的比例。默认为 0.1。
- n_iter_no_change:连续多少次迭代损失函数未下降时停止迭代。默认为 5。
- epsilon:当 loss='huber' 或 'epsilon_insensitive' 时,使用的 epsilon 值。默认为 0.1。
在实践中,SGDRegressor 的调参需要根据具体的数据集和任务来进行,一般需要进行多轮实验来找到最优参数组合。同时,使用随机梯度下降法进行模型训练时,需要仔细调节学习率等参数,以避免过拟合或欠拟合。
from sklearn.datasets import load_diabetes from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error# 加载糖尿病数据集 diabetes = load_diabetes()# 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, test_size=0.2, random_state=42)# 线性回归模型 lr_model = LinearRegression() lr_model.fit(X_train, y_train)# 在测试集上预测并评估模型 y_pred = lr_model.predict(X_test) mse = mean_squared_error(y_test, y_pred)# 输出结果 print("均方误差:", mse)在这个示例中,我们直接将糖尿病数据集划分为训练集和测试集,并使用
LinearRegression进行线性回归。最后在测试集上计算均方误差。由于数据没有进行标准化处理,预测结果的单位与目标变量的单位相同,因此均方误差的量级也比标准化后的数据要大。
LinearRegression() 和 SGDRegressor对比
LinearRegression() 和 SGDRegressor 都是用于线性回归的算法。
LinearRegression() 是最基本的线性回归算法,它的实现基于最小二乘法。它通过拟合一个线性方程来预测响应变量(因变量)和一个或多个解释变量(自变量)之间的关系。在这种情况下,这个线性方程是一个一次函数,它可以表示为 y = a1x1 + a2x2 + … + anxn + b,其中 x1, x2, …, xn 是解释变量,y 是响应变量,a1, a2, …, an 是回归系数,b 是截距。在这种算法中,目标是找到最佳的回归系数和截距,以使误差最小化。它的计算比较简单,但如果数据集非常大,它的性能可能会受到影响。
相比之下,SGDRegressor 是一种基于随机梯度下降(SGD)的线性回归算法。它是一种迭代算法,每次迭代时只考虑一个样本,并在每次迭代中更新回归系数,直到达到最小化误差的目标。因此,它比 LinearRegression() 更适合大数据集,并且可以在线更新模型。SGDRegressor 可以支持不同类型的损失函数,如平方误差损失函数和 Huber 损失函数等。通过调整不同的超参数,如学习率和正则化参数,可以调整 SGDRegressor 的性能。
在实践中,如果数据集较小,使用 LinearRegression() 可能更容易实现,同时也更容易解释模型。如果数据集较大,则 SGDRegressor 更具有优势,因为它可以更快地收敛,并且可以在线更新模型。
下面是一个 LinearRegression 和 SGDRegressor 的对比示例:
from sklearn.datasets import load_diabetes from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression, SGDRegressor from sklearn.metrics import mean_squared_error# 加载糖尿病数据集 diabetes = load_diabetes()# 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, test_size=0.2, random_state=42)# 线性回归模型 lr_model = LinearRegression() lr_model.fit(X_train, y_train)# 随机梯度下降回归器 sgd_model = SGDRegressor(random_state=42) sgd_model.fit(X_train, y_train)# 在测试集上预测并评估模型 lr_pred = lr_model.predict(X_test) lr_mse = mean_squared_error(y_test, lr_pred)sgd_pred = sgd_model.predict(X_test) sgd_mse = mean_squared_error(y_test, sgd_pred)print(lr_mse," ",sgd_mse)
过拟合与欠拟合
- 过拟合:一个假设在训练数据上能够获得比其他假设更好的拟合, 但是在测试数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂)
- 欠拟合:一个假设在训练数据上不能获得更好的拟合,并且在测试数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单)
岭回归
岭回归是一种用于处理多重共线性(即自变量之间存在高度相关性)和数据过拟合问题的线性回归模型。在标准的最小二乘线性回归中,当数据集存在多重共线性时,回归系数可能会出现很大的方差,导致预测结果不可靠;当模型复杂度过高时,也容易出现过拟合现象,导致模型在训练集上表现很好但在测试集上表现较差。
岭回归通过在损失函数中添加一个正则化项,对回归系数进行限制,从而减小方差,降低过拟合的风险。正则化项的大小由超参数α控制,α越大,正则化项的影响越大,回归系数越接近于0,从而减少方差的同时增加偏差。因此,超参数α的选择非常重要,通常需要通过交叉验证等方法进行调参。
在岭回归中,alpha是一个正则化参数,用于控制模型的复杂度。alpha的值越大,模型的正则化项的影响就越大,模型的复杂度就会降低,从而减少过拟合的风险。相反,如果alpha的值太小,模型就容易过拟合。因此,alpha需要通过交叉验证等技术进行调整,以找到最优的值。
下面是使用岭回归来解决过拟合和欠拟合问题的代码示例:
from sklearn.linear_model import Ridge from sklearn.model_selection import GridSearchCV from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split from sklearn.metrics import mean_squared_error# 加载数据集 boston = load_boston() X, y = boston.data, boston.target# 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 定义岭回归模型 ridge = Ridge()# 定义超参数范围 params = {'alpha': [0.1, 1, 10, 100, 1000]}# 使用网格搜索选择最优超参数 grid = GridSearchCV(estimator=ridge, param_grid=params, cv=5, scoring='neg_mean_squared_error') grid.fit(X_train, y_train)# 输出最优超参数和对应的负均方误差 print('Best alpha:', grid.best_params_['alpha']) print('Best negative mean squared error:', grid.best_score_)# 在测试集上评估模型性能 y_pred = grid.predict(X_test) mse = mean_squared_error(y_test, y_pred) print('Test set mean squared error:', mse)在这个示例中,我们使用sklearn中的Ridge模型来进行岭回归,通过网格搜索来选择最优的超参数alpha,使用均方误差(MSE)作为评价指标。在最优超参数下,我们在测试集上得到了较低的MSE,说明岭回归可以有效地降低过拟合风险,提高模型泛化能力。
应用场景
线性回归是机器学习中最基础的模型之一,掌握它的原理和应用非常重要。除了前面讨论到的内容外,以下是一些可能有帮助的补充信息:
- 线性回归假设自变量和因变量之间的关系是线性的,因此在实际应用中,需要根据数据的特点来判断是否适合使用线性回归模型,或者是否需要对数据进行变换。
- 在实际应用中,线性回归模型往往需要进行特征工程来提高模型的预测性能。特征工程包括特征选择、特征变换、特征组合等技术,可以从数据中提取更有用的信息,以提高模型的准确性。
- 在处理非线性问题时,可以使用多项式回归模型,它通过对原始特征进行多项式变换来引入非线性项,从而拟合更加复杂的关系。不过需要注意的是,过高的多项式阶数可能会导致过拟合,因此需要通过交叉验证等技术来选择合适的阶数。
- 线性回归模型的性能指标通常采用均方误差(MSE)或平均绝对误差(MAE)等指标来衡量。在实际应用中,还需要考虑到模型的解释性、鲁棒性等因素来进行综合评估。
- 在使用线性回归模型时,需要注意数据集的划分和样本的随机性,否则可能会导致模型的偏差或方差过大,从而影响预测性能。
相关文章:
Python机器学习入门笔记(3)—— 线性回归
目录 线性回归 算法简述 LinearRegression() API SGDRegressor API LinearRegression() 和 SGDRegressor对比 过拟合与欠拟合 岭回归 应用场景 线性回归 算法简述 线性回归是一种基本的机器学习算法,它用于建立自变量和因变量之间的线性关系模型。它假设…...

Java:顶级Java应用程序服务器 — Tomcat、Jetty、GlassFish、WildFly
如果你想编写Java web应用程序,首先需要做出一个艰难的决定:选择运行应用程序的Java应用程序服务器。什么是应用服务器?一般来说,应用程序服务器执行Java应用程序。在操作系统中启动它们,然后将应用程序部署到其中。将应用程序服…...
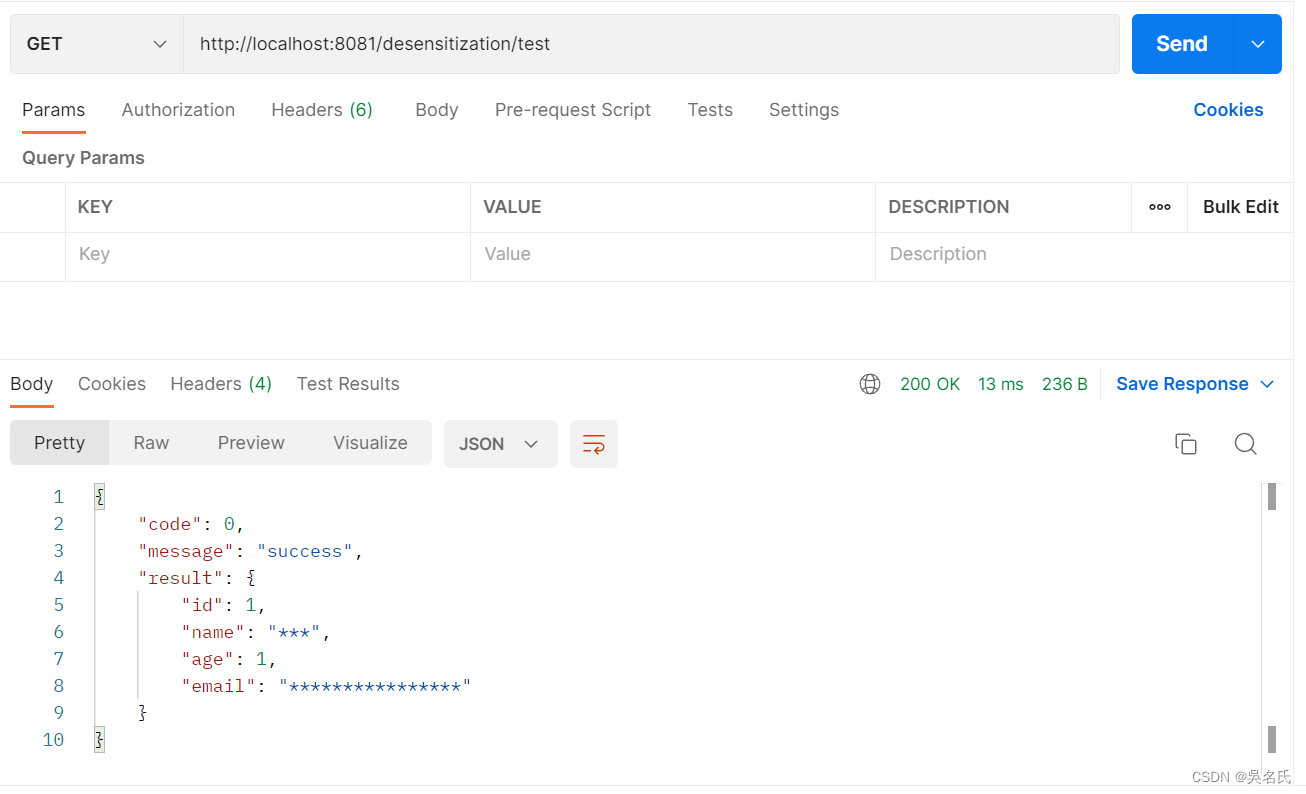
如何在SpringBoot项目上让接口返回数据脱敏,一个注解即可
1 背景需求是某些接口返回的信息,涉及到敏感数据的必须进行脱敏操作2 思路①要做成可配置多策略的脱敏操作,要不然一个个接口进行脱敏操作,重复的工作量太多,很显然违背了“多写一行算我输”的程序员规范。思来想去,定…...
python 之 海龟绘图(turtle)
注:从个人博客园移植而来 使用简介 python 2.6引入的一个简单的绘图工具,俗称为海龟绘图。3.x以上使用的话,可通过pip进行安装,命令为: pip/pip3 install turtle如果出现如下错误: 解决方式: …...
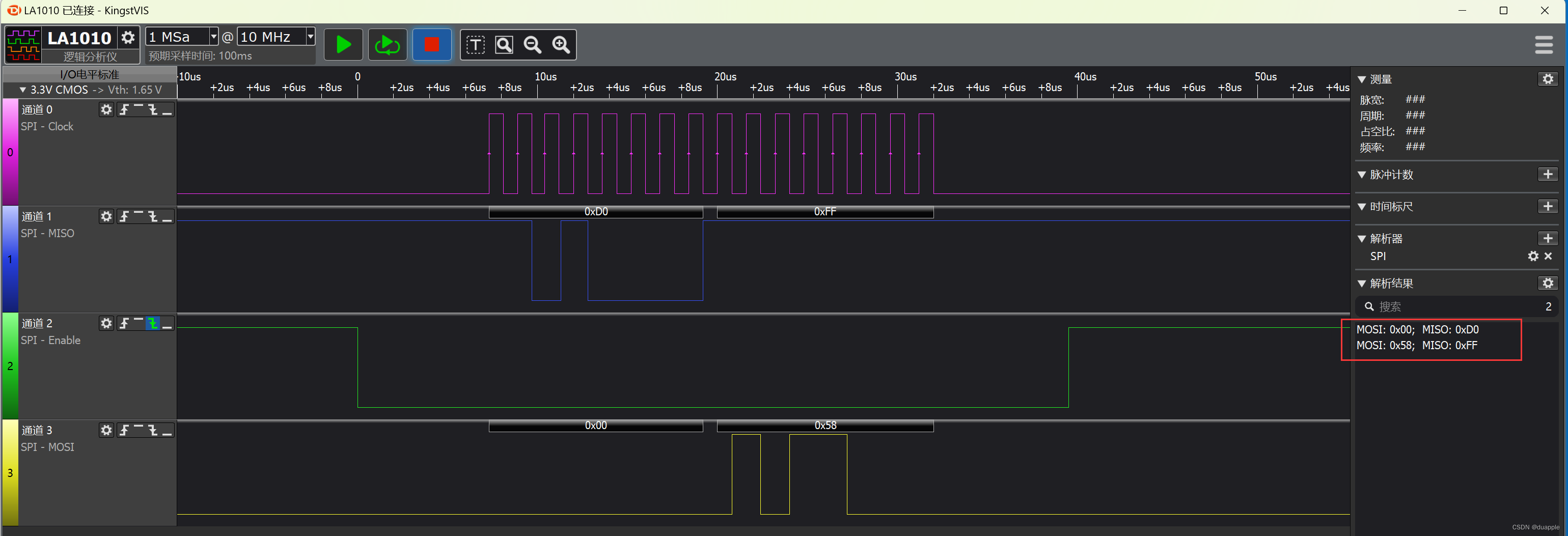
RT-Thread SPI使用教程
RT-Thread SPI 使用教程 实验环境使用的是正点原子的潘多拉开发板。 SPI从机设备使用的是BMP280温湿度大气压传感器。 使用RT-Thread Studio搭建基础功能。 1. 创建工程 使用RT-Thread Studio IDE创建芯片级的工程。创建完成后,可以直接编译下载进行测试。 2.…...

shiro使用——整合spring
shiro使用——整合spring 1. 引入相关配置 <dependency><groupId>org.apache.shiro</groupId><artifactId>shiro-spring</artifactId><version>1.9.1</version></dependency>2. 自定义Realm类 继承AuthorizingRealm 并重写相…...

2023-02-20 leetcode-AccountsMerge
摘要: 记录对leetcode-AccountsMerge的反思 要求: Given a list accounts, each element accounts[i] is a list of strings, where the first element accounts[i][0] is a name, and the rest of the elements are emails representing emails of the account. * Now, w…...

中国高速公路行业市场规模及未来发展趋势
中国高速公路行业市场规模及未来发展趋势编辑中国高速公路行业市场规模正在迅速增长。随着中国经济的快速发展和城市化的加速,对交通基础设施的需求也在不断增加。高速公路是最有效的交通工具,可以大大缩短交通时间,提高出行效率。因此&#…...
佳能iC MF645CX彩色激光多功能打印机报E302-0001故障码检修
故障现象: 一台佳能iC MF645CX彩色激光多功能一体机开机报E302-0001故障代码,如果设备未恢复,请联系经销商或客户支持中心。 维修分析: 佳能iC MF645CX彩色激光多功能一体机开机报E302-0001故障代码的...

加密越来越简单——用JavaScript实现数据加密和解密
加密越来越简单——用JavaScript实现数据加密和解密概念常用算法1. MD5加密算法2. SHA-1加密算法3. AES加密算法代码示例结论总结在当今互联网的世界中,安全性越来越受到关注,数据加密成为了必不可少的一环。Javascript作为前端开发的主要语言之一&#…...

线程池的使用场景
学习整理线程池的使用场景。...

图像分割算法
图像分割算法阈值分割固定阈值自适应阈值大津阈值(OTSU)最大熵阈值连通域分析区域生长分水岭阈值分割、连通域分析、区域生长、分水岭 阈值分割 固定阈值、自适应阈值(adaptiveThreshold)、大津阈值(OTSU)、最大熵阈值(KSW) 固定阈值 固定阈值的调用函数: //Input…...
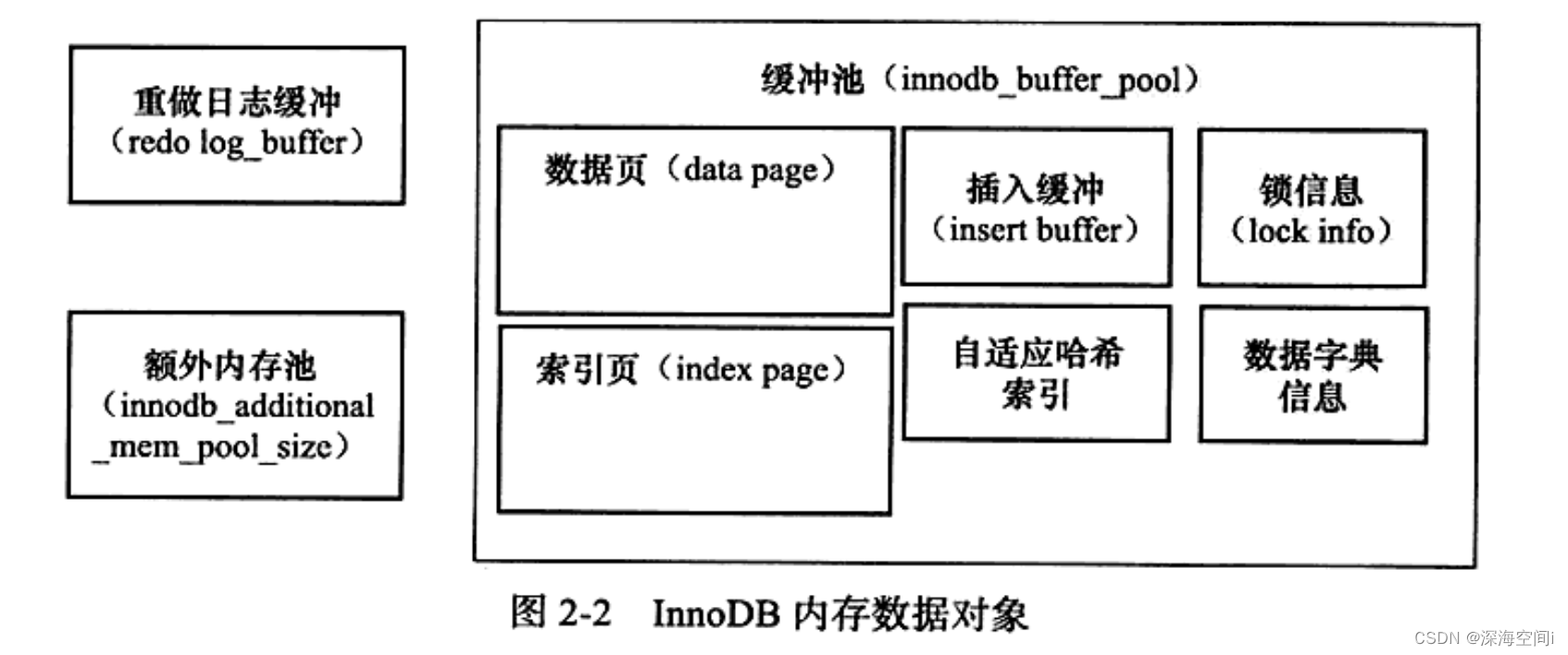
《mysql技术内幕:innodb存储引擎》笔记
任何时候Why都比What重要;不要相信任何的“神话”,学会自己思考;不要墨守成规,大部分人都知道的事情可能是错误的;不要相信网上的传言,去测试,根据自己的实践做出决定;花时间充分地思考,敢于提出质疑。1.MYSQL被设计为一个单进程多…...

windows与linux系统ntp服务器配置
一. windows 打开windows终端(管理员),顺序输入以下指令 net stop w32time w32tm /unregister w32tm /register net start w32time w32tm /resync net stop w32time net start w32timewin r 输入regedit,打开注册表。 ①将HKEY_…...
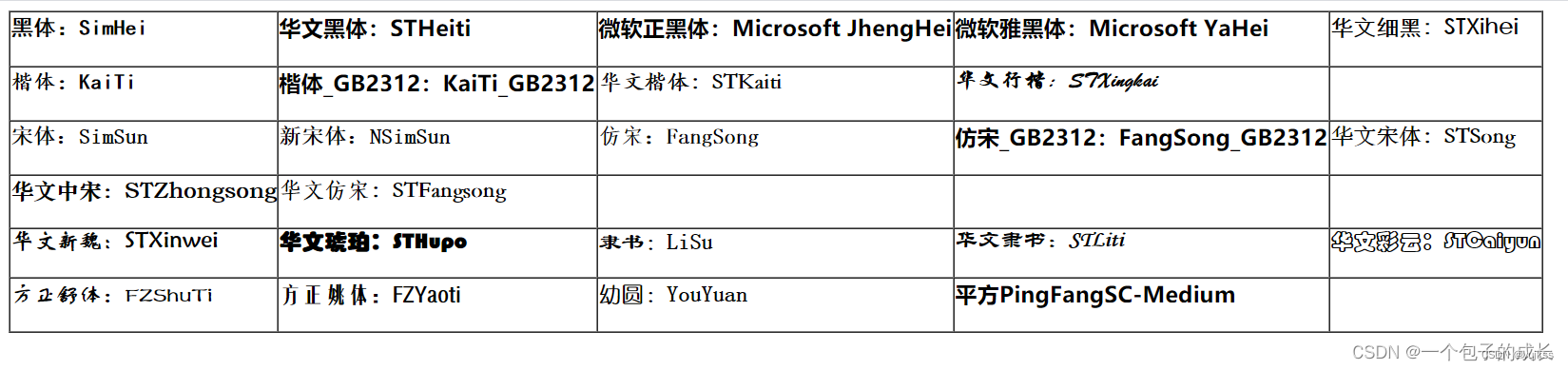
html常用font-family设置字体样式
<table border"1" cellpadding"0" cellspacing"0" ><tr><td><h3 style"font-family: 黑体;">黑体:SimHei</h3></td><td><h3 style"font-family: 华文黑体;">华…...
数据库事务AICD以及隔离级别
目录一.事务的ACID二.隔离级别三.并发事务中的问题1.脏写2.脏读3.不可重复读4.幻读四.MVCC机制五.读锁与写锁六.大事务的影响七.事务优化一.事务的ACID 原子性(Atomicity):一个事务中的所有操作,要么全部成功,要么失败全部回滚,不…...
VScode之ssh基础配置)
(4)VScode之ssh基础配置
VScode和SSH基础配置问题集合 Author:onceday date:2022年8月31日 本文记录linux的ssh和vscode开发环境搭建之路。 参考文档: 离线安装vscode Once Day CSDN博客关于x86、x86_64/x64、amd64和arm64/aarch64 Bogon 简书arm64和aarch64之间…...

springcloud-1环境搭建、service provider
搭建项目环境创建新项目,选择archetype-webapp,创建一个父项目,该父项目会去管理多个微服务模块(module)项目设置Settings->Editor->File Encoding:Global/Project Encoding 改为UTF-8Default encoding for properties files:默认属性文…...
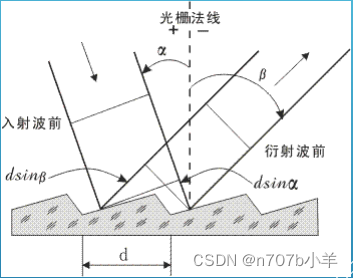
光谱仪工作过程及重要参数定义
标题光谱仪工作过程CCD、PDA薄型背照式BT-CCD狭缝Slit暗电流Dark Current分辨率Resolution色散Dispersion光栅和闪耀波长Grating波长精度、重复性和准确度Precision带宽Band widthF数F/#光谱仪工作过程 CCD、PDA 电荷耦合器件(Charger Coupled Device,缩…...
W800|iot|HLK-W800-KIT-PRO|AliOS|阿里云| |官方demo|学习(1):板载AliOS系统快速上手
板载系统简介 HLK-W800-KIT-PRO 是海凌科电子面向开发者,采用了联盛德 w800 方案,带有一个RGB三色灯,集成了 CHT8305C 温湿度传感器的多功能开发板,用户可以在上面学习、研究嵌入式系统和物联网产品的开发,本套设备运行…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
