7-周赛333总结
7-周赛333总结
还是只过了前两题,第三题又写了好久好久,然后也不知道错在了哪里,只过了部分题解,也许是思考不全面吧。下次也许先做第四题更好…第四题今天花了点时间 做出来了个大概 开心 :happy:
合并两个二维数组 - 求和法【LC2570】
给你两个 二维 整数数组
nums1和nums2.
nums1[i] = [idi, vali]表示编号为idi的数字对应的值等于vali。nums2[i] = [idi, vali]表示编号为idi的数字对应的值等于vali。每个数组都包含 互不相同 的 id ,并按 id 以 递增 顺序排列。
请你将两个数组合并为一个按 id 以递增顺序排列的数组,并符合下述条件:
- 只有在两个数组中至少出现过一次的 id 才能包含在结果数组内。
- 每个 id 在结果数组中 只能出现一次 ,并且其对应的值等于两个数组中该 id 所对应的值求和。如果某个数组中不存在该 id ,则认为其对应的值等于
0。返回结果数组。返回的数组需要按 id 以递增顺序排列。
-
思路:双指针、归并排序
使用双指针指向数组
nums1和nums2中的元素,优先取id较小的指针对应的二元组,如果两个指针指向的id相同,那么二元组的值为两个指针对应的值之和 -
实现
由于不确定有多少元素重复,因此可以先将结果存储在动态数组中,最后在将结果赋值至int数组中
class Solution {public int[][] mergeArrays(int[][] nums1, int[][] nums2) {int n = nums1.length, m = nums2.length;List<int[]> list = new ArrayList<>();int i = 0, j = 0;while (i < n || j < m){int[] add = new int[2];if (j == m || (i < n && nums1[i][0] < nums2[j][0])){add[0] = nums1[i][0];add[1] = nums1[i][1];i++;}else if(i == n || (j < m && nums1[i][0] > nums2[j][0])){add[0] = nums2[j][0];add[1] = nums2[j][1];j++;}else{add[0] = nums1[i][0];add[1] = nums1[i][1] + nums2[j][1]; i++;j++;}list.add(add);}int[][] res = new int[list.size()][2];for (int k = 0; k < list.size(); k++){res[k] = list.get(k);}return res;} }- 复杂度
- 时间复杂度:O(n+m)O(n+m)O(n+m)
- 空间复杂度:O(n+m)O(n+m)O(n+m),动态数组的额外空间
- 复杂度
将整数减少到零需要的最少操作数【LC2571】
给你一个正整数
n,你可以执行下述操作 任意 次:
n加上或减去2的某个 幂返回使
n等于0需要执行的 最少 操作数。如果
x == 2i且其中i >= 0,则数字x是2的幂。
-
思路:贪心
由于操作只能加上或减去
2的某个 幂,因此采用位运算的方式解决此题,求取n的二进制形式所有1变为0时所需要的操作数。从最低位开始,找到每个值为1的位,假定为第iii位,而第一个为0的位为第jjj位,当连续1的个数等于1时,采用减幂消除1;当连续1的个数大于1时,采用加幂进位的方式消除1
-
当连续1的个数等于1时,减去该位对应的幂,将该位变为0,所需要的操作数为1次;
-
而当连续1的个数大于1时,可以通过加2的最低1位对应的幂进位,此时所有的连续1变为0,然后产生了进位,第jjj位变为1,所需要的操作数也为1次;【使用减幂方式所需要的操作数为j−ij-ij−i,而使用进位的方式所需要的操作数为2次,并且消除进位产生的1的同时可能会消除更多的1,因此连续1的个数大于1时,采用进位的方式消除1时最优的】
局部最优和全局最优
- 局部最优:将连续的所有1变为0的次数最少
- 全局最优:将
n变为0的操作数最少
-
-
实现
class Solution {public int minOperations(int n) {// 如果遇到连续1个数大于1时,进位 操作数加1// 连续1个数等于1,直接减操作int res = 0;int i = 0;while (n != 0){// 找到从左到右第一个1while (((n >> i) & 1) == 0){i++;}int j = i;// 找到从左到右第一个0while (((n >> j) & 1) == 1){j++;}if (j - i > 1){n += Math.pow(2, i);res++;}else{n -= Math.pow(2, i);res++;}i = j;}return res;} }- 复杂度
- 时间复杂度:O(logn)O(logn)O(logn)
- 空间复杂度:O(1)O(1)O(1)
- 复杂度
-
优化:
使用位运算获取最低位
lb = n & -n,然后使用n & (lb << 1)) > 0判断是否有连续1class Solution {public int minOperations(int n) {int ans = 1;while ((n & (n - 1)) > 0) { // n 不是 2 的幂次int lb = n & -n;if ((n & (lb << 1)) > 0) n += lb; // 多个连续 1else n -= lb; // 单个 1++ans;}return ans;} }作者:灵茶山艾府 链接:https://leetcode.cn/problems/minimum-operations-to-reduce-an-integer-to-0/solutions/2120204/ji-yi-hua-sou-suo-by-endlesscheng-cm6l/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。class Solution {public int minOperations(int n) {int ans = 0;while (n != 0) { int lb = n & -n;if ((n & (lb << 1)) > 0) n += lb; // 多个连续 1else n -= lb; // 单个 1++ans;}return ans;} }
*无平方子集计数【LC2572】
给你一个正整数数组
nums。如果数组
nums的子集中的元素乘积是一个 无平方因子数 ,则认为该子集是一个 无平方 子集。无平方因子数 是无法被除
1之外任何平方数整除的数字。返回数组
nums中 无平方 且 非空 的子集数目。因为答案可能很大,返回对109 + 7取余的结果。
nums的 非空子集 是可以由删除nums中一些元素(可以不删除,但不能全部删除)得到的一个数组。如果构成两个子集时选择删除的下标不同,则认为这两个子集不同。
-
思路:
-
如果两个无平方因子数的最大公因数为1,那么它们可以存在一个子集当中。
-
由于本题中
nums的数值大小小于等于30,因此可以对该范围的数进行预处理,判断每个数是否是无平方因子数,如果是无平方因子数则求出每个数对应质因数的集合,并使用状态压缩法表示,当mask的第iii位为1是第iii个质数在集合中;如果不是无平方因子数,那么mask设为-1。 -
题意可转化为「选一些不相交的质数集合,它们的并集恰好为集合 jjj的方案数」。【01背包问题】
物品即为每个数字分解的质因数集合,背包容量为背包可以容纳的质因数对应的状态码,当物品对应质因数集合是背包容量的子集时,则可以向该背包放入该物品
-
-
二维动态规划
-
确定dp数组(dp table)以及下标的含义
dp[i][j]表示 从前i个元素中取若干元素,质因数出现的情况为j的方案数。
-
确定递推公式
-
不放元素i:dp[i][j]=dp[i−1][j]dp[i][j] = dp[i-1][j]dp[i][j]=dp[i−1][j]
-
放元素i:当
nums[i]对应的状态码为mask,前一个状态与mask不能相交,因此前一个状态码为mask^jdp[i][j]=dp[i−1][j⊕mask]dp[i][j] = dp[i-1][j\oplus mask]dp[i][j]=dp[i−1][j⊕mask]
动态规划公式为
dp[i][j]=dp[i−1][j]+dp[i−1][j⊕mask]dp[i][j] = dp[i-1][j]+ dp[i-1][j \oplus mask] dp[i][j]=dp[i−1][j]+dp[i−1][j⊕mask] -
-
dp数组如何初始化
dp[0][0] = 1; -
确定遍历顺序
二维dp,遍历顺序不影响结果
先遍历物品,再遍历背包重量,确定物品i能否放进背包j中
-
举例推导dp数组
最后结果即为∑dp[n−1][j]\sum dp[n-1][j]∑dp[n−1][j]
class Solution {private static final int[] PRIMES = new int[]{2, 3, 5, 7, 11, 13, 17, 19, 23, 29};private static final int MOD = (int) 1e9 + 7, MX = 30, N_PRIMES = PRIMES.length, M = 1 << N_PRIMES;private static final int[] NSQ_TO_MASK = new int[MX + 1]; // NSQ_TO_MASK[i] 为 i 对应的质数集合(用二进制表示)static {for (int i = 2; i <= MX; ++i)for (int j = 0; j < N_PRIMES; ++j) {int p = PRIMES[j];if (i % p == 0) {if (i % (p * p) == 0) { // 有平方因子NSQ_TO_MASK[i] = -1;break;}NSQ_TO_MASK[i] |= 1 << j; // 把 j 加到集合中}}}public int squareFreeSubsets(int[] nums) {int n = nums.length;int[][] dp = new int[n + 1][M]; // f[i][j] 表示恰好组成集合 j 的方案数 // Arrays.fill(dp[0], 1);// 空集的方案数为 1dp[0][0] = 1;for (int i = 0; i < n; i++) {for (int j = 0; j < M; j++) dp[i + 1][j] = dp[i][j];// 不选 maskint mask = NSQ_TO_MASK[nums[i]];if (mask >= 0) // x 是 NSQfor (int j = mask; j <= M - 1; j++){if ((j | mask) == j) // mask 是 j 的子集dp[i + 1][j] = (dp[i + 1][j] + dp[i][j ^ mask]) % MOD; // 选 mask}}int ans = 0;for (int j = 0; j < M; j++){ans = (ans + dp[n][j]) % MOD;}return ans - 1;} }- 复杂度
- 时间复杂度:O(nM)O(nM)O(nM),n为数组长度,M为状态压缩后包含质因子情况的总数
- 空间复杂度:O(n∗M)O(n*M)O(n∗M),dp数组的额外空间
-
-
优化:一维dp
先遍历物品,再从后往前遍历背包重量,确定物品i能否放进背包j中
class Solution {private static final int[] PRIMES = new int[]{2, 3, 5, 7, 11, 13, 17, 19, 23, 29};private static final int MOD = (int) 1e9 + 7, MX = 30, N_PRIMES = PRIMES.length, M = 1 << N_PRIMES;private static final int[] NSQ_TO_MASK = new int[MX + 1]; // NSQ_TO_MASK[i] 为 i 对应的质数集合(用二进制表示)static {for (int i = 2; i <= MX; ++i)for (int j = 0; j < N_PRIMES; ++j) {int p = PRIMES[j];if (i % p == 0) {if (i % (p * p) == 0) { // 有平方因子NSQ_TO_MASK[i] = -1;break;}NSQ_TO_MASK[i] |= 1 << j; // 把 j 加到集合中}}}public int squareFreeSubsets(int[] nums) {var f = new int[M]; // f[j] 表示恰好组成集合 j 的方案数f[0] = 1; // 空集的方案数为 1for (int x : nums) {int mask = NSQ_TO_MASK[x];if (mask >= 0) // x 是 NSQfor (int j = M - 1; j >= mask; --j)if ((j | mask) == j) // mask 是 j 的子集f[j] = (f[j] + f[j ^ mask]) % MOD; // 不选 mask + 选 mask}var ans = 0L;for (int v : f) ans += v;return (int) ((ans - 1) % MOD); // -1 去掉空集} }作者:灵茶山艾府 链接:https://leetcode.cn/problems/count-the-number-of-square-free-subsets/solutions/2121032/liang-chong-xie-fa-01bei-bao-zi-ji-zhuan-3ooi/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。- 复杂度
- 时间复杂度:O(nM)O(nM)O(nM),n为数组长度,M为状态压缩后包含质因子情况的总数
- 空间复杂度:O(M)O(M)O(M),dp数组的额外空间
- 复杂度
找出对应 LCP 矩阵的字符串【LC2573】
对任一由
n个小写英文字母组成的字符串word,我们可以定义一个n x n的矩阵,并满足:
lcp[i][j]等于子字符串word[i,...,n-1]和word[j,...,n-1]之间的最长公共前缀的长度。给你一个
n x n的矩阵lcp。返回与lcp对应的、按字典序最小的字符串word。如果不存在这样的字符串,则返回空字符串。对于长度相同的两个字符串
a和b,如果在a和b不同的第一个位置,字符串a的字母在字母表中出现的顺序先于b中的对应字母,则认为字符串a按字典序比字符串b小。例如,"aabd"在字典上小于"aaca",因为二者不同的第一位置是第三个字母,而'b'先于'c'出现。
按列扫描
-
思路:按规则按列逐个构造
-
首先,由于题目要求返回的合法字符串是字典顺序最小的,因此第一个字符一定是
a -
然后从开头到末尾逐个构造字符,当我们构造第iii个字符时,前j∈[0,i−1]j \in [0,i-1]j∈[0,i−1]个字符是确定的,那么当lcp[j][i]>0lcp[j][i]>0lcp[j][i]>0时,第iii个字符就等于第jjj个字符,直接退出本层循环;如果第iii个字符与前面的字符均不相同,那么第iii个字符为当前已经构造的最大字符的下一个字符。
-
需要注意的是,如果构造的字符大于
z,那么不符合题意,返回空字符串 -
最后还需要验证构造的字符串是否满足矩阵,如果不满足,也返回空字符串。
验证方法为动态规划
- 如果s[i]=s[j]s[i]=s[j]s[i]=s[j],那么lcp[i][j]=lcp[i+1][j+1]+1lcp[i][j]=lcp[i+1][j+1]+1lcp[i][j]=lcp[i+1][j+1]+1
- 如果s[i]≠s[j]s[i]\ne s[j]s[i]=s[j],那么lcp[i][j]=0lcp[i][j]=0lcp[i][j]=0
-
-
实现
按列扫描lcp数组
class Solution {public String findTheString(int[][] lcp) {int n = lcp.length;// 如果矩阵对称并且值小于等于字符串长度时,有满足的字符串【不全面】// for (int i = 0; i < n; i++){// for (int j = 0; j < n; j++){// if (lcp[i][j] != lcp[j][i] || lcp[i][j] > Math.min(n - i, n - j)){// return "";// }// if (i == j && lcp[i][j] != n - i){// return "";// }// }// }StringBuilder sb = new StringBuilder();sb.append('a');// 第0个字符一定是a char c = 'a';for (int i = 1; i < n; i++){// 按顺序找第1-n-1个字符for (int j = 0; j < i; j++){// 根据与前面字符的关系确定 int count = lcp[j][i];// s[j,j+count-1] s[i,i+count-1] if (count > 0){// s[i] = s[j]sb.append(sb.charAt(j)); break; }}if (sb.length() < i + 1){if (c == 'z') return "";c += 1;sb.append(c);}}// 验证for (int i = n - 1; i >= 0; --i)for (int j = n - 1; j >= 0; --j) {int actualLCP = sb.charAt(i) != sb.charAt(j) ? 0 : i == n - 1 || j == n - 1 ? 1 : lcp[i + 1][j + 1] + 1;if (lcp[i][j] != actualLCP) return "";}return sb.toString();}}- 复杂度
- 时间复杂度:O(n2)O(n^2)O(n2)
- 空间复杂度:O(1)O(1)O(1)
- 复杂度
按行扫描
-
思路
- 如果lcp[i][j]>0lcp[i][j]>0lcp[i][j]>0时,s[i]s[i]s[i]一定等于s[j]s[j]s[j],而第一个字符一定是
a,因此可以先扫描lcp[0],如果lcp[0][j]>0lcp[0][j]>0lcp[0][j]>0,那么该字符一定是a - 然后进行下一轮,本轮的字符为
b,找到从左到右数首个没有填入字符的位置iii,将其填入当前已经构造的最大字符的下一个字符,然后再扫描lcp[i],如果lcp[0][j]>0lcp[0][j]>0lcp[0][j]>0,那么填入本轮的字符。往复循环,直至iii大于字符串长度,或者字符超过了z - 如果退出循环时,iii小于nnn,表示没有构造完,直接返回空字符串
- 最后,进行验证,验证方法同上
- 如果lcp[i][j]>0lcp[i][j]>0lcp[i][j]>0时,s[i]s[i]s[i]一定等于s[j]s[j]s[j],而第一个字符一定是
-
实现
class Solution {public String findTheString(int[][] lcp) {int i = 0, n = lcp.length;var s = new char[n];for (char c = 'a'; c <= 'z'; ++c) {while (i < n && s[i] > 0) ++i;if (i == n) break; // 构造完毕for (int j = i; j < n; ++j)if (lcp[i][j] > 0) s[j] = c;}while (i < n) if (s[i++] == 0) return ""; // 没有构造完// 直接在原数组上验证for (i = n - 1; i >= 0; --i)for (int j = n - 1; j >= 0; --j) {int actualLCP = s[i] != s[j] ? 0 : i == n - 1 || j == n - 1 ? 1 : lcp[i + 1][j + 1] + 1;if (lcp[i][j] != actualLCP) return "";}return new String(s);} }作者:灵茶山艾府 链接:https://leetcode.cn/problems/find-the-string-with-lcp/solutions/2120175/tan-xin-gou-zao-yan-zheng-o1e-wai-kong-j-82ik/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。- 复杂度
- 时间复杂度:O(n2)O(n^2)O(n2)
- 空间复杂度:O(1)O(1)O(1)
- 复杂度
相关文章:

7-周赛333总结
7-周赛333总结 还是只过了前两题,第三题又写了好久好久,然后也不知道错在了哪里,只过了部分题解,也许是思考不全面吧。下次也许先做第四题更好…第四题今天花了点时间 做出来了个大概 开心 :happy: 合并两个二维数组 - 求和法【…...

电子招标采购系统源码—互联网+招标采购
智慧寻源 多策略、多场景寻源,多种看板让寻源过程全程可监控,根据不同采购场景,采取不同寻源策略, 实现采购寻源线上化管控;同时支持公域和私域寻源。 询价比价 全程线上询比价,信息公开透明,可…...

SQL注入和XSS攻击
1、SQL注入 所谓SQL注入,就是通过把SQL命令插入到Web表单递交或输入域名或页面请求的查询字符串,最终达到欺骗服务器执行恶意的SQL命令。 我们永远不要信任用户的输入,我们必须认定用户输入的数据都是不安全的,我们都需要对用户输…...

js Map的使用
前言:Map数据集可以理解为加强版的对象 一、for...of 1、对象不能用于for of,因其没有部署Iterator接口;其他数据集如:数组、Map、Set、Iterator对象等都可以用for...of2、使用for...of的优势: for of的循环体中可以…...

企业应该怎么管理香港服务器?
做好服务器管理,往往能为站长避免很多麻烦。用户租用服务器,除了希望它快速而安全,还有就是如何才能得到优质及时的售后和指导建议了。服务器供应商只提供服务器管理的基础服务,负责提供硬件、带宽和电力等服务,服务器…...
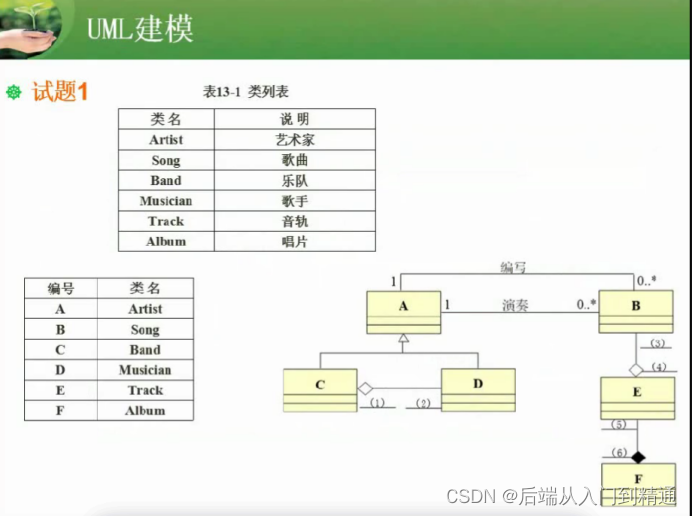
软件设计(十四)-UML建模(上)
软件设计(十三)-原码、反码、补码、移码https://blog.csdn.net/ke1ying/article/details/129115844?spm1001.2014.3001.5501 UML建模包含:用例图,类图与对象图,顺序图,活动图,状态图ÿ…...
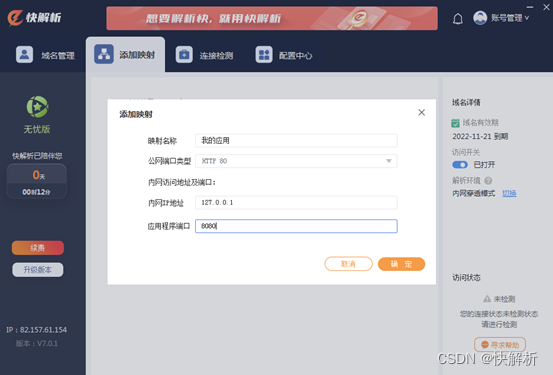
本地主机搭建服务器后如何让外网访问?快解析内网端口映射
本地主机搭建应用、部署服务器后,在局域网内是可以直接通过计算机内网IP网络地址进行连接访问的,但在外网电脑和设备如何访问呢?由于内网环境下,无法提供公网IP使用,外网访问内网就需要一个内外网转换的介质。这里介绍…...
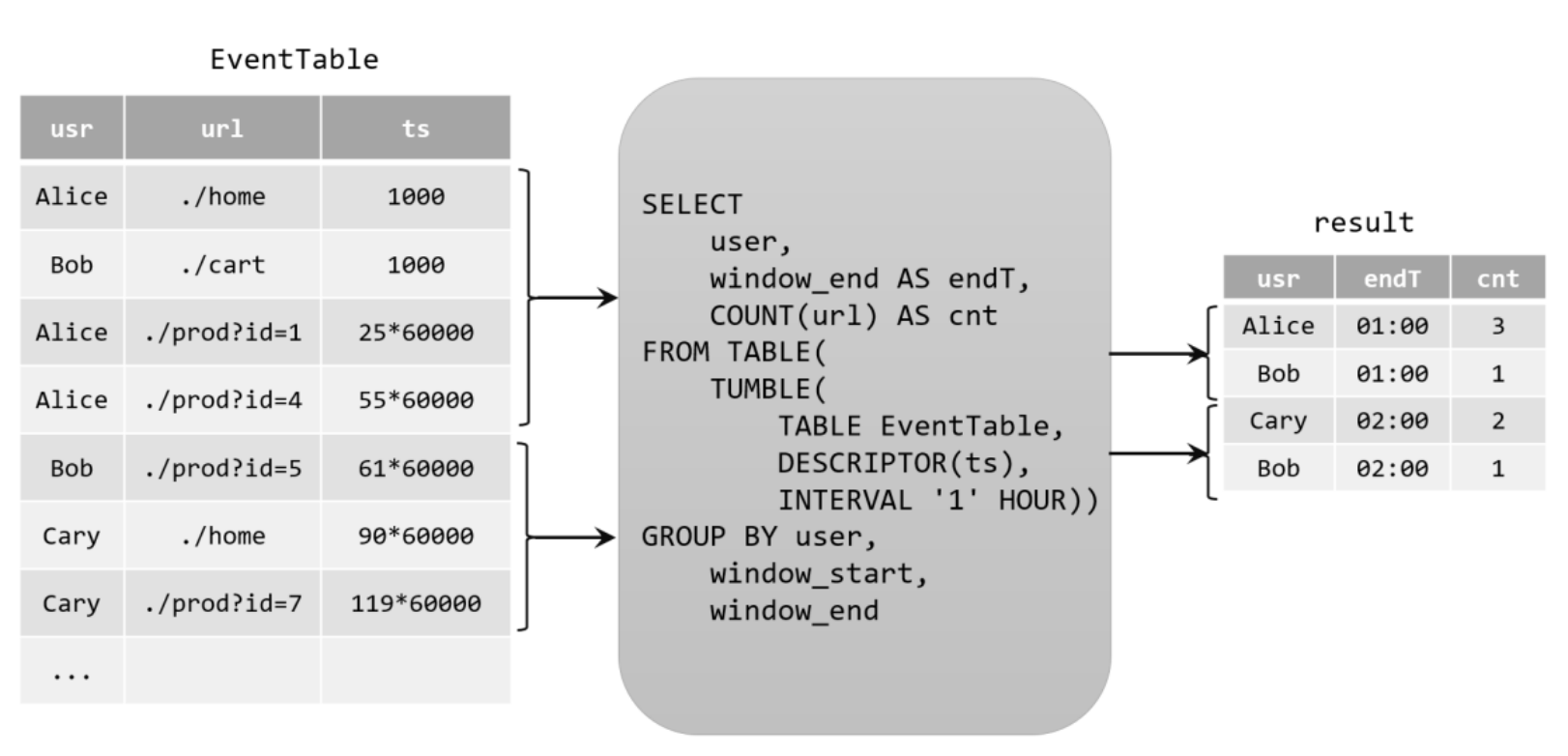
Flink-Table API 和 SQL(基本API、流处理的表、时间属性和窗口、聚合查询、联结查询、函数、SQL客户端、连接到外部系统)
文章目录Table API 和 SQL快速上手基本 API程序架构创建表环境创建表表的查询输出表表和流的转换流处理中的表动态表和持续查询将流转换成动态表原理用 SQL 持续查询-更新查询&追加查询将动态表转换为流(Append-only、Retract、Upsert)时间属性和窗口事件时间处理时间窗口&…...

C++入门:数据抽象
数据抽象是指,只向外界提供关键信息,并隐藏其后台的实现细节,即只表现必要的信息而不呈现细节。数据抽象是一种依赖于接口和实现分离的编程(设计)技术。让我们举一个现实生活中的真实例子,比如一台电视机&a…...

WRF进阶:使用IO选项控制WRF变量输出/WRF指定变量输出添加/删除
Registry文件 WRF模式在运行求解时,会涉及到大量的数据变量运算,而这些数据变量的管理、规定、控制则需要依赖于WRF的Registry文件,简单来说,它可以理解为管理WRF数据结构的“数据字典”("Active data-dictionar…...

一文读懂功率放大器(功率放大器的特性是什么意思)
功率放大器是一种电子放大器,旨在增加给定输入信号的功率幅度。功率放大器一般要求得到一定的不失真或者较小失真的输出功率,在大信号状态下进行工作,主要是输出较大功率。功率放大器的特性介绍:1、增益功率放大器的增益主要是指放…...

微信小程序阻止页面返回(包滑动、自动返回键)
这个场景还是挺有意思的,比如某多多,只要你点左上角的返回 好家伙,满满又 花不了 的优惠券就来了,让你拥有一种消费最划算的感觉。 如果你的场景比较简单,只是对左上角的返回进行监听,只需要关闭自带的导航…...

视频直播美颜sdk的发展史
视频直播美颜sdk的出现是必然的,它的诞生就是为了让更多用户能够更好地体验到视频直播带给大家的快乐,可以说视频直播美颜sdk的发展和用户体验有着紧密联系。今天,小编不聊技术,咱们来聊一下视频直播美颜sdk的诞生以及发展历程。 …...

【Mysql】存储过程
【Mysql】存储过程 文章目录【Mysql】存储过程1.存储过程1.1 存储过程概述1.2 特点1.3 基本语法1.3.1 创建1.3.2 调用1.3.3 查看1.3.4 删除1.4 变量1.4.1 系统变量1.4.2 用户定义变量1.4.3 局部变量1.5 if1.6 参数1.7 case1.8 循环1.8.1 while1.8.2 repeat1.8.3 loop1.9 游标1.…...
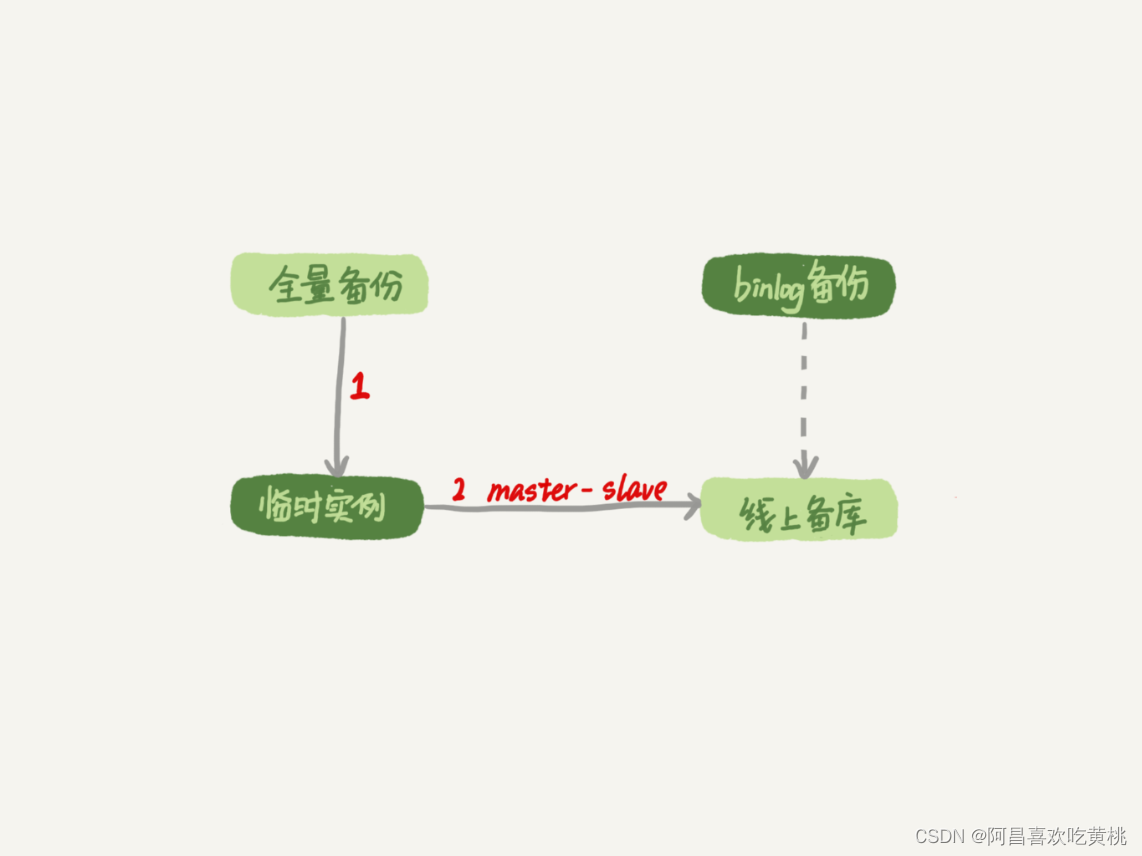
Day895.MySql误删数据还原方案 -MySQL实战
MySql误删数据还原方案 Hi,我是阿昌,今天学习记录的是关于MySql误删数据还原方案的内容。 传统的高可用架构是不能预防误删数据的,因为主库的一个 drop table 命令,会通过 binlog 传给所有从库和级联从库,进而导致整…...

Java方法引用
2 方法引用 在使用Lambda表达式的时候,我们实际上传递进去的代码就是一种解决方案:拿参数做操作那么考虑一种情况: 如果我们在Lambda中所指定的操作方案,已经有地方存在相同方案,没有必要再写重复逻辑,如usePrintable…...

C++教程之迭代器Iterator
前言 之前的两篇文章我们主要了解了vector和string的相关知识,从中我们知道可以通过下标来访问vector的元素或者string的字符,但是除了这种方式还有一种更为通用的方式获取元素,那就是迭代器,这篇文章就会简单介绍迭代器的相关内…...

容联七陌:ChatGPT大模型能力为智能客服带来新方向
科技云报道原创。 近几个月来,大众对ChatGPT预期的持续走高,也影响到了智能客服领域公司的命运。 一方面,ChatGPT的出现为智能客服场景带来了更加“智能”的可能性;但另一方面,有人认为ChatGPT完全可以替代现有的智能…...
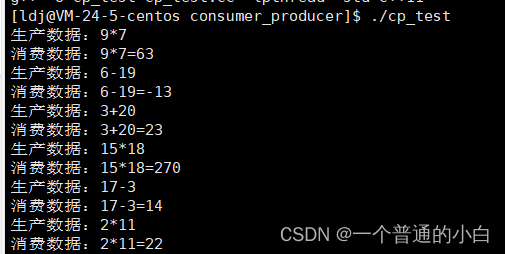
【Linux 多线程同步】使用同步和互斥实现生产消费模型
目录 1.同步的接口 2.多线程但是按顺序来执行 3.生产消费模型 4.使用互斥加同步实现生产消费模型 (采用环形队列) 同步:在保证数据安全的前提下,让线程能够按照某种特定的顺序访问临界资源,从而有效避免饥饿问题 …...
:)
【TypeScript】TypeScript的接口和对象类型(interface):
文章目录一、使用接口约束的时候不能多一个属性也不能少一个属二、重名interface 可以合并,继承三、可选属性 使用?操作符四、任意属性 [propName: string]五、只读属性 readonly,是不允许被赋值的只能读取六、添加函数一、使用接口约束的时候不能多一个…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
