Java中synchronized基本介绍和细节讨论。使用Synchronized来解决售票超卖问题
基本介绍
线程同步机制:在多线程编程下,一些敏感数据不允许被多个现在在同一时刻访问,此时就使用同步访问机制,保证数据在任何同一时刻最多只有一个进程访问,以保证数据的完整性。(即:当有一个线程在对内存操作时,其他的线程都不允许对这个内存地址进行操作,指代该线程完成操作,其他的线程才能对内存地址进行操作)
细节讨论
- 关键字synchronized来与对象的互斥锁联系。当某个对象来用synchronized修饰时,表明该对象在任何一时刻只能由一个线程访问
- 同步的局限性:导致程序的执行效率低,因为同一时刻只能执行一个线程
- sychronized可以修饰方法也可以修饰代码块,分别称为同步方法和同步代码块。一般情况下建议使用同步代码块,因为这样的效率要高一些
- 同步方法(非静态)的锁对象可以是this,也可以是其他对象(要求是同一个对象)
- 同步方法(静态的)的锁对象是当前类本身
使用synchronized来处理售票时线程同步的问题:
代码:
public class Threads {public static void main(String[] args) {//会出现票超卖现象,原因:当我们还有1张票时,可能一下子来了2个线程,此时判断是否<=0时都不小于,所以继续往下执行卖票,导致票超卖现象Windows windows = new Windows();//同一个对象Thread thread1 = new Thread(windows);thread1.setName("窗口1");//设置线程的名字 Thread thread2 = new Thread(windows);thread2.setName("窗口1");Thread thread3 = new Thread(windows);thread3.setName("窗口3");thread1.start();thread2.start();thread3.start();}
}class Windows implements Runnable {private static int tickets = 100;//共享100张票private /*static*/ Boolean loop = true;//控制run方法变量public /*static*/ void sell() {//同步方法
// Object object = new Object();synchronized (/*当方法为静态时锁对象是当前类本身为:Windows.class*/this/*当为非静态方法时也可以为object,因为object是这个类的对象,是同一个对象*/) {if (tickets <= 0) {System.out.println("没票了");loop = false;return;}try {Thread.sleep(10);} catch (InterruptedException e) {e.printStackTrace();}System.out.println(Thread.currentThread().getName() + "卖了一张票,还剩" + (--tickets));}}@Overridepublic void run() {while (loop) {sell();
// synchronized (this) {//同步代码块
// if (tickets <= 0) {
// System.out.println("没票了");
// loop = false;
// return;
// }
//
// try {
// Thread.sleep(10);
// } catch (InterruptedException e) {
// e.printStackTrace();
// }
//
// System.out.println("窗口" + Thread.currentThread().getName() + "卖了一张票,还剩" + (--tickets));
// }}}
}
注意:一定要是同一个对象,如上述的windows。如果是不同的对象的话,相当于是不同的对象锁了,也就是不只一把锁,各用各的,当然就起不到线程同步了。比如:你要进厕所去方便,现在这个房间的门就相当于是对象锁,只能等里面的人出来后你在进入。若此时是不同的对象的话,就相当于有不同的门,也就是说现在这个厕所有不同的门可以进入了,那样就起不到防护机制了。
相关文章:

Java中synchronized基本介绍和细节讨论。使用Synchronized来解决售票超卖问题
基本介绍 线程同步机制:在多线程编程下,一些敏感数据不允许被多个现在在同一时刻访问,此时就使用同步访问机制,保证数据在任何同一时刻最多只有一个进程访问,以保证数据的完整性。(即:当有一个线程在对内存…...
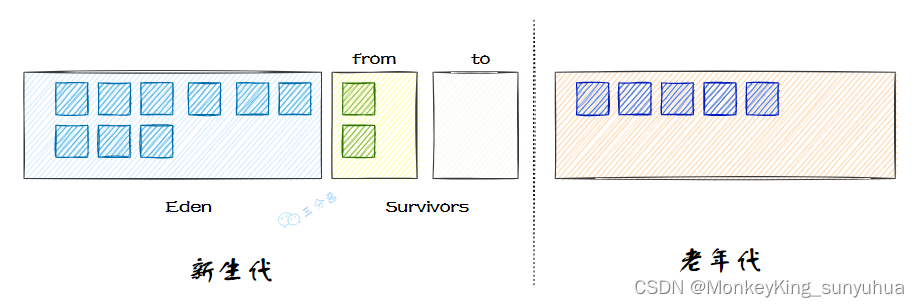
java内存分区
按照垃圾收集,将 Java 堆划分为**新生代 (Young Generation)和老年代(Old Generation)**两个区域, 新生代存放存活时间短的对象,而每次回收后存活的少量对象,将会逐步晋升到老年代中…...

【JavaScript】V8 引擎解析 JavaScript 的过程
V8 是由 Google 开发的 JavaScript 引擎,用于执行 JavaScript 代码。它被广泛应用于 Chrome 浏览器和 Node.js 等环境。V8 的解析和执行过程是一个复杂的流程,以下是其大致步骤: 词法分析(Lexical Analysis)࿱…...

Qt:界面实时响应鼠标拖动绘制
采用双缓冲实现界面实时响应鼠标的拖动绘制。 思想如下:首先需要两张画布pix和tempPix,他们都是QPixmap实例;pix用来保存初始界面或上一阶段以完成的绘制;tempPix用来作为鼠标拖动时的实时界面绘制;当鼠标左键按下后拖…...
Docker拉取RocketMQ及可视化界面
本文介绍Docker拉取RocketMQ及可视化界面操作步骤 Linux下安装Docker请参考:Linux安装Docker 文章目录 安装namesrv创建挂载目录授权相关权限拉取镜像运行容器查看运行情况 安装Broker创建挂载目录及配置文件目录授权相关权限创建配置文件运行容器查看运行情况 安装…...
花5分钟判断,你的Jmeter技能是大佬还是小白!
jmeter 这个工具既可以做接口的功能测试,也可以做自动化测试,还可以做性能测试,其主要用途就是用于性能测试。但是,有些公司和个人,就想用 jmeter 来做接口自动化测试。 你有没有想过呢? 下面我就给大家讲…...
macOS - 安装 Python 及地址
文章目录 Python 官方安装包Pip3Applications - PythonMiniconda多个python环境有多种方式安装 python,比如 Python 官方包、anaconda、miniconda、brew 等 这里记录使用 Python 官方包进行安装,和 miniconda 安装方式,以及安装后 各执行文件、安装包的地址。 明确这些地址后…...

前端组件库造轮子——Tree组件开发教程
前端组件库造轮子——Tree组件开发教程 前言 本系列旨在记录前端组件库开发经验,我们的组件库项目目前已在Github开源,下面是项目的部分组件。文章会详细介绍一些造组件库轮子的技巧并且最后会给出完整的演示demo。 文章旨在总结经验,开源分…...

java打war包、jar包方式,java运行war包、jar包方式
Java spring boot部署到生产环境有两种常见方式 1打jar包,使用了内置的tomcat服务器,流程简单 2打war包,可以放标准tomcat服务器中 jar包 1pom.xml新增 <build><plugins><plugin><groupId>org.springframework.b…...
“超级AI助手:全新提升!中文NLP训练框架,快速上手,海量训练数据,ChatGLM-v2、中文Bloom、Dolly_v2_3b助您实现更智能的应用!”
“超级AI助手:全新提升!中文NLP训练框架,快速上手,海量训练数据,ChatGLM-v2、中文Bloom、Dolly_v2_3b助您实现更智能的应用!” 1.简介 目标:基于pytorch、transformers做中文领域的nlp开箱即用…...

空时自适应处理用于机载雷达——机载阵列雷达信号环境(Matla代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

lib61850 学习笔记一 (概念)
IEC61850 定义60多种服务满足变电站通信需求。支持在线获取数据模型,也支持IED水平通信(GOOSE报文) 术语定义 间隔 bay: 变电站由据应公共功能紧密连接的子部分组成。 例如 介于进线或者 出线 和母线之间的断路器;二条母线之间…...

【深度学习】半监督学习 Efficient Teacher: Semi-Supervised Object Detection for YOLOv5
https://arxiv.org/abs/2302.07577 https://github.com/AlibabaResearch/efficientteacher 文章目录 AbstractIntroductionRelated WorkEfficient TeacherDense Detector Abstract 半监督目标检测(SSOD)在改善R-CNN系列和无锚点检测器的性能方面取得了成…...

vue3鼠标拖拽滑动效果
第一步 在utils下面新建一个directives.js文件,然后引入如下代码 const dragscroll (el) > {el.onmousedown ev > {const disX ev.clientX;const disY ev.clientY; // 需要上下移动可以加const originalScrollLeft el.scrollLeft;const originalScroll…...
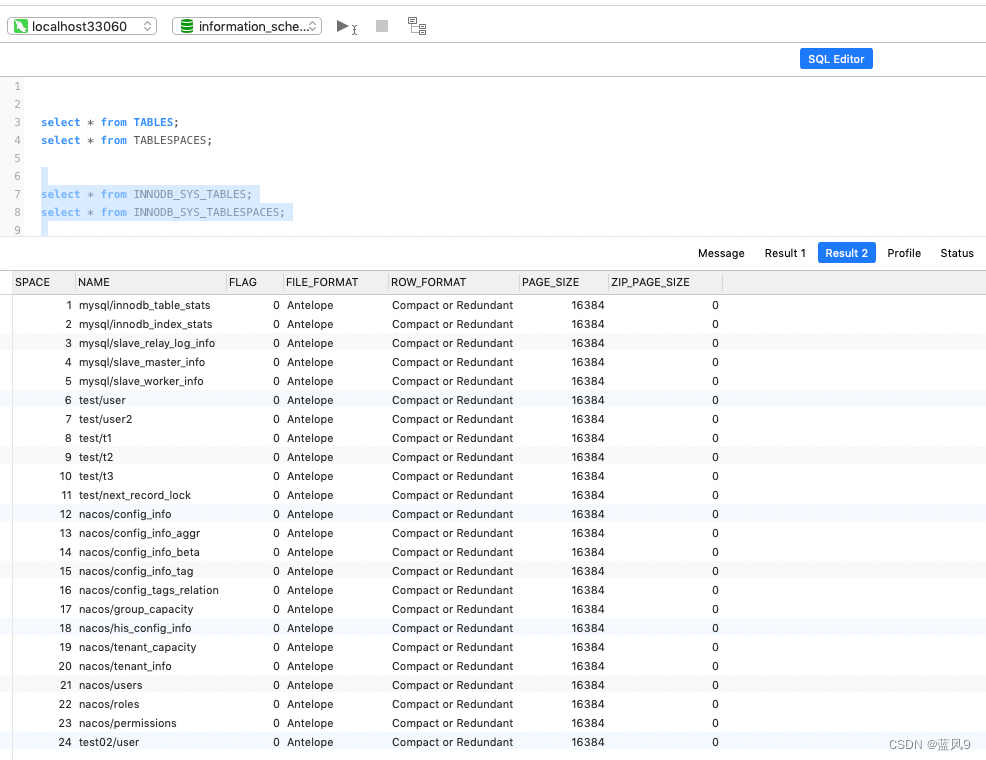
08 通过从 库1 复制 *.ibd 到 库2 导致 mysql 启动报错
前言 呵呵 最近同事有这样的一个需求 需要将 库1 的一张表 复制到 库2 然后 我想到了 之前一直使用的通过复制这个库的 data 文件来进行数据迁移的思路, 是需要复制这个 库对应的 data 目录下的数据文件, 以及 ibdata1 文件 然后 我又在想 这里的场景能否也使用这里的额方式…...

一生一芯9——ubuntu22.04安装valgrind
这里安装的valgrind版本是3.19.0 下载安装包 在选定的目录下打开终端,输入以下指令 wget https://sourceware.org/pub/valgrind/valgrind-3.19.0.tar.bz2直至下载完成 解压安装包 输入下面指令解压安装包 tar -xvf valgrind-3.19.0.tar.bz2.tar.bz2注…...
)
STM32中BOOT的作用 (芯片死锁解决方法)
BOOT stm32中具有BOOT1和BOOT0 作用 BOOT是stm32单片机的启动模式, 通过不同组合模式,共有三种启动方式。 一般来说就是指我们下好程序后,重启芯片时,SYSCLK的第4个上升沿,BOOT引脚的值将被锁存。用户可以通过设置B…...
基于YOLOv8模型和DarkFace数据集的黑夜人脸检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要:基于YOLOv8模型和DarkFace数据集的黑夜人脸检测系统可用于日常生活中检测与定位黑夜下的人脸,利用深度学习算法可实现图片、视频、摄像头等方式的目标检测,另外本系统还支持图片、视频等格式的结果可视化与结果导出。本系统采用YOLOv8目…...

C++中<iostream> 的cin >> str 和<string>的getline(cin, str) 用来读取用户输入的两种不同方式的不同点
C中<iostream> 的cin >> str 和<string>的getline(cin, str) 用来读取用户输入的两种不同方式的不同点 <string>的getline()函数语法如下【https://cplusplus.com/reference/string/string/getline/】: istream& getl…...

微信报修系统有什么优势?怎么提升企业维修工作效率与管理水平?
随着智能化时代的到来,企业、事业单位的现代化设备数量和种类不断增加,原本繁琐的报修、填写记录、检修管理等工作得以简化。从发起报修到维修,以及维修之后给予评价的整个过程,通过手机微信报修系统均能看到,既省时又…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
