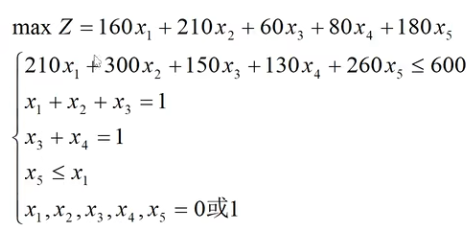数学建模(四)整数规划—匈牙利算法
目录
一、0-1型整数规划问题
1.1 案例
1.2 指派问题的标准形式
2.2 非标准形式的指派问题
二、指派问题的匈牙利解法
2.1 匈牙利解法的一般步骤
2.2 匈牙利解法的实例
2.3 代码实现
一、0-1型整数规划问题
1.1 案例
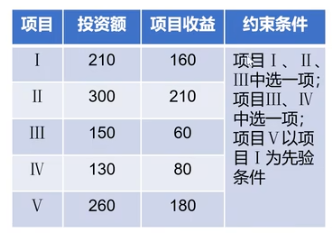
投资问题:
有600万元投资5个项目,收益如表,求利润最大的方案?
设置决策变量:
模型:
指派问题:
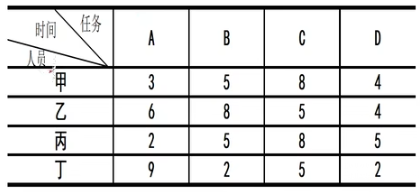
甲乙丙丁四个人,ABCD四项工作,要求每人只能做一项工作,每项工作只由一人完成,问如何指派总时间最短?
设置决策变量:
模型:
约束条件:
1.2 指派问题的标准形式
标准的指派问题:
有n个人和n项工作,已知第i个人做第j项工作的代价为cj(i,j=1,…..,n),要求每项工作只能交与其中一人完成,每个人只能完成其中一项工作,问如何分配可使总代价最少?
指派问题标准求解形式:
(1) 指派问题的系数矩阵

(2)决策变量的设置

(3)指派问题的解矩阵
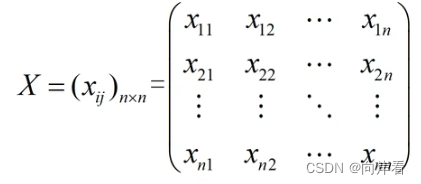
指派问题的可行解中,每行每列有且仅有一个1。
(4)标准模型
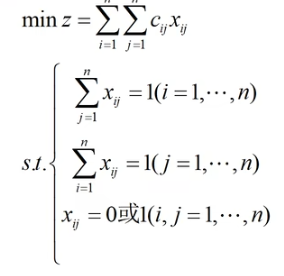
2.2 非标准形式的指派问题
(1)最大化指派问题
例如:求利润,只需找出最大元素,令最大元素减去所有元素,构建一个新的系数矩阵即可。
中最大元素为m,令
。
(2)人数和工作数不等
人少工作多:添加虚拟的 “人”,代价都为0。
人多工作少:添加虚拟的工作,代价都为0。
(3)一个人可做多件工作
该人可化为几个相同的 “人”。
(4)某工作一定不能由某人做
该人做该工作的相应代价取足够大M。例如,将某人做某工作代价设为负值。
二、指派问题的匈牙利解法
匈牙利法是一种求解指派问题的简便解法,它利用了矩阵中0元素的定理。若从系数矩阵的一行(列)各元素中分别减去该行(列)的最小元素,得到新矩阵。以新矩阵为系数矩阵求得的最优解和用原矩阵求得的最优解相同。
2.1 匈牙利解法的一般步骤
第一步:变换指派问题的系数(也称效率)矩阵()为(
),使在(
)的各行各列中都出现0元素,即
- (1) 从矩阵(
)的每行元素都减去该行的最小元素。
- (2) 再从所得新系数矩阵的每列元素中减去该列的最小元素。
第二步:进行试指派,以寻求最优解。
在()中找尽可能多的独立0元素(即行和列中只有这一个0元素),若能找出n个独立0元素,就以这n个独立0元素对应解矩阵(
)中的元素为1,其余为0,这就得到最优解。找独立0元素,常用的步骤为:
- (1) 从只有一个0元素的行开始,给这个0元素加圈,记作
,然后划去
所在列的其它0元素,记作
 。这表示这列所代表的任务已指派完,不必再考虑别人了。
。这表示这列所代表的任务已指派完,不必再考虑别人了。 - (2) 给只有一个0元素的列中的0元素加圈,记作
,然后划去
所在行的0元素,记作
 。
。 - (3) 反复进行(1),(2)两步,直到尽可能多的0元素都被圈出和划掉为止。
- (4) 若仍有没有划圈的0元素,且同行(列)的0元素至少有两个,则从剩有0元素最少的行(列)开始,比较这行各0元素所在列中0元素的数目,选择0元素少的那列的这个0元素加圈。然后划掉同行同列的其它0元素。可反复进行,直到所有0元素都已圈出和划掉为止。
- (5) 若
元素的数目m等于矩阵的阶数n,那么这指派问题的最优解已得到。若m<n,则转入下一步。
第三步:作最少的直线覆盖所有0元素。
- (1) 对没有
的行打√号;
- (2) 对已打√号的行中所有含
 元素的列打√号。
元素的列打√号。 - (3) 再对打有√号的列中含
元素的行打√号。
- (4) 重复(2),(3)直到得不出新的打√号的行、列为止。
- (5) 对没有打√号的行画横线,有打√号的列画纵线,这就得到覆盖所有0元素的最少直线数
。
应等于m,转第四步。若不相等,说明试指派过程有误,回到第二步(4)。
第四步:变换矩阵()以增加0元素。
在没有被直线覆盖的所有元素中找出最小元素,然后打√各行都减去这最小元素。打√各列都加上这最小元素(以保证系数矩阵中不出现负元素)。新系数矩阵的最优解和原问题仍相同。转回第二步,直到找出最优解。
2.2 匈牙利解法的实例
甲乙丙丁四人要完成四项工作A、B、C、D,每人只能完成一项工作,要求完成总时间最短。

匈牙利解法:
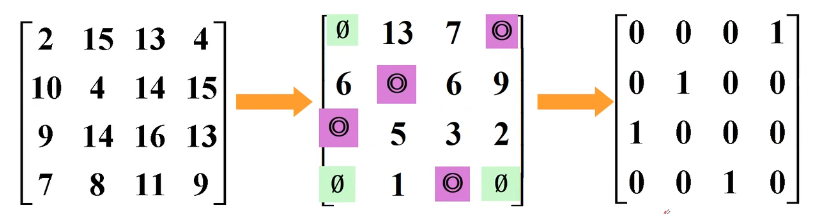
第一步:减去最小值。
第二步:加圈和划掉,比较圈数是否等于矩阵的阶数。
等于,则输出最优值, 否则,转到第三步重整矩阵。
2.3 代码实现
c=[3 8 2 10 3;8 7 2 9 7;6 4 2 7 5; 8 4 2 3 5;9 10 6 9 10];%系数矩阵c=c(:); %把矩阵c转化为向量 a=zeros(10,25);for i=1:5 % 实现循环运算
a(i,(i-1)*5+1:5*i)=1;
a(5+i,i:5:25)=1;
end % 此循环把指派问题转换为线性规划问题b=ones(10,1); [x,y]=linprog(c,[],[],a,b,zeros(25,1),ones(25,1));X=reshape(x,5,5)opt=y
输出:

相关文章:

数学建模(四)整数规划—匈牙利算法
目录 一、0-1型整数规划问题 1.1 案例 1.2 指派问题的标准形式 2.2 非标准形式的指派问题 二、指派问题的匈牙利解法 2.1 匈牙利解法的一般步骤 2.2 匈牙利解法的实例 2.3 代码实现 一、0-1型整数规划问题 1.1 案例 投资问题: 有600万元投资5个项目&…...

openGauss学习笔记-47 openGauss 高级数据管理-权限
文章目录 openGauss学习笔记-47 openGauss 高级数据管理-权限47.1 语法格式47.2 参数说明47.3 示例 openGauss学习笔记-47 openGauss 高级数据管理-权限 数据库对象创建后,进行对象创建的用户就是该对象的所有者。数据库安装后的默认情况下,未开启三权分…...
开始MySQL之路——MySQL 事务(详解分析)
MySQL 事务概述 MySQL 事务主要用于处理操作量大,复杂度高的数据。比如说,在人员管理系统中,你删除一个人员,你即需要删除人员的基本资料,也要删除和该人员相关的信息,如信箱,文章等等…...

注解和class对象和mysql
注解 override 通常是用在方法上的注解表示该方法是有重写的 interface 表示一个注解类 比如 public interface override{} 这就表示是override是一个注解类 target 修饰注解的注解表示元注解 deprecated 修饰某个元素表示该元素已经过时了 1.不代表该元素不能用了&…...
【桌面小屏幕项目】ESP32开发环境搭建
视频教程链接: 【【有手就行系列】嵌入式单片机教程-桌面小屏幕实战教学 从设计、硬件、焊接到代码编写、调试 ESP32 持续更新2022】 https://www.bilibili.com/video/BV1wV4y1G7Vk/?share_sourcecopy_web&vd_source4fa5fad39452b08a8f4aa46532e890a7 一、esp…...

CSS 滚动容器与固定 Tabbar 自适应的几种方式
问题 容器高度使用 px 定高时,随着页面高度发生变化,组件展示的数量不能最大化的铺满,导致出现底部留白。容器高度使用 vw 定高时,随着页面宽度发生变化,组件展示的数量不能最大化的铺满,导致出现底部留白…...

IP 地址追踪工具
IP 地址跟踪工具是一种网络实用程序,允许您扫描、跟踪和获取详细信息,例如 IP 地址的 MAC 和接口 ID。IP 跟踪解决方案通过使用不同的网络扫描协议来检查网络地址空间来收集这些详细信息。一些高级 IP 地址跟踪器软件(如 OpUtils)…...

最新企业网盘产品推荐榜发布
随着数字化发展,传统的文化存储方式已无法跟上企业发展的步伐。云存储的出现为企业提供了新的文件管理存储模式。企业网盘作为云存储的代表性工具,被越来越多的企业所青睐。那么在众多企业网盘产品中,企业该如何找到合适的企业网盘呢…...

实用的面试经验分享:程序员们谈论他们的面试历程
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
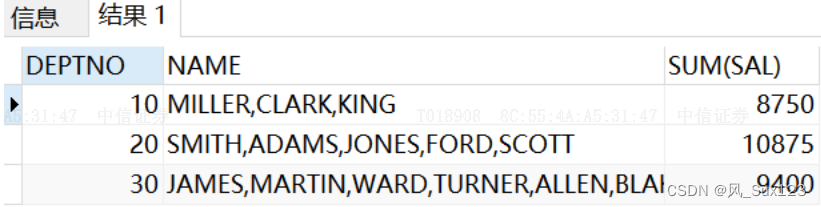
6.oracle中listagg函数使用
1. 作用 可以实现行转列,将多列数据聚合为一列,实现数据的压缩 2. 语法 listagg(measure_expr,delimiter) within group ( order by order_by_clause); 解释: measure_expr可以是基于任何列的表达式 delimiter分隔符,…...

习题练习 C语言(暑期)
编程能力小提升! 前言一、转义字符二、重命名与宏定义三、三目运算符四、计算日期到天数转换五、计算字符串长度六、宏定义应用七、const常量八、C语言基础九、const常量(二)十、符号运算十一、记负均正十二、SWITCH,CASE十三、错…...

C++中虚函数表的概念
当一个类对象指针调用虚函数时,这就涉及到 运行时多态 的概念。这意味着实际调用的函数取决于对象的实际类型,而不仅仅是指针的静态类型。 假设我们有以下的类层次结构: class Base { public:virtual void print() {std::cout << &qu…...
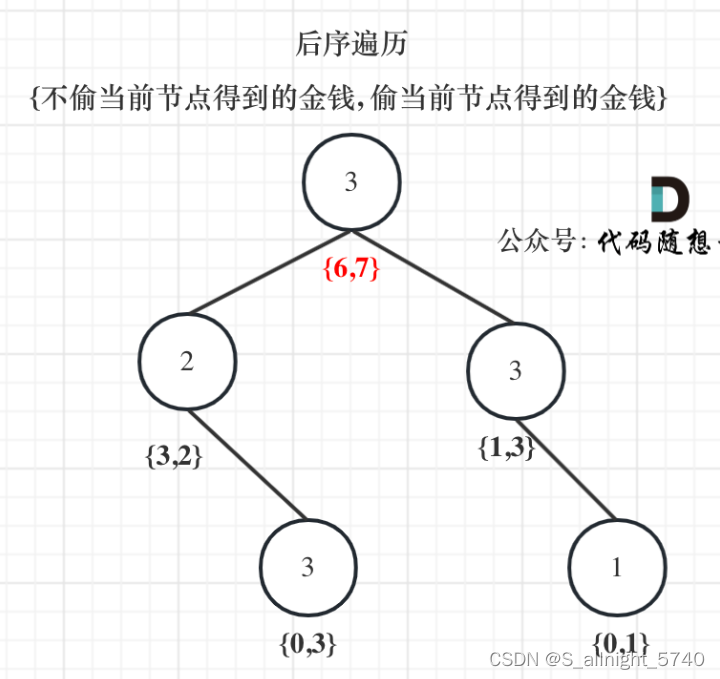
代码随想录算法训练营第四十八天 | 198.打家劫舍,213.打家劫舍II,337.打家劫舍III
代码随想录算法训练营第四十八天 | 198.打家劫舍,213.打家劫舍II,337.打家劫舍III 198.打家劫舍213.打家劫舍II337.打家劫舍III 198.打家劫舍 题目链接 视频讲解 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金ÿ…...

uniapp项目实战系列(1):导入数据库,启动后端服务,开启代码托管
目录 前言前期准备1.数据库的导入2.运行后端服务2.1数据库的后端配置2.2后端服务下载依赖,第三方库2.3启动后端服务 3.开启gitcode代码托管 ✨ 原创不易,还希望各位大佬支持一下! 👍 点赞,你的认可是我创作的动力&…...
在互联网+的背景下,企业如何创新客户服务?
随着互联网的发展,开始数字化转型的潮流,移动互联网平台为各个行业带来了发展的新方向。企业有了移动互联网的加持,为客户提供了更好的服务。当移动互联网平台能够为客户提供更好的用户体验时,相应地,客户也给企业带来…...

国内的化妆品核辐射检测
化妆品核辐射物质检测是指检测化妆品中的放射性物质,包括放射性核素和放射性同位素。这些放射性物质主要来源于环境中的放射性污染,如空气、水和土壤中的放射性物质,以及化妆品生产过程中的放射性污染,如原料、设备、工艺等。化妆…...

春秋云镜:CVE-2019-9042(Sitemagic CMS v4.4 任意文件上传漏洞)
一、题目 靶标介绍: Sitemagic CMS v4.4 index.php?SMExtSMFiles 存在任意文件上传漏洞,攻击者可上传恶意代码执行系统命令。 进入题目: admin/admin /index.php?SMExtSMFiles&SMTemplateTypeBasic&SMExecModeDedicated&SMFil…...

20230828工作日志:
今天遇到了很多问题,下次可以做得更好更快的几个地方: 1 sql语句的检查 肯定要先在navicate 里执行看,是否有语法错误。即使没有,也还是要注意一些问题:IDEA里换行的时候,“后面要空一格,如果连…...

flink on yarn 部署
需要jars -rwxr-xrwx 3 root supergroup 58284 2022-11-30 03:44 /lib/flink/commons-cli-1.5.0.jar -rw-r--r-- 3 root supergroup 48497 2022-12-10 03:04 /lib/flink/flink-cep-scala_2.12-1.14.3.jar -rw-r--r-- 3 root supergroup 189468 2022-12-10…...

postgresql基于postgis常用空间函数
1、ST_AsGeoJSON 图元转geojson格式 select ST_AsGeoJSON(l.geom) from g_zd l limit 10 2、 ST_Transform 坐标转换 select st_transform(l.shape, 3857) from sde_wf_cyyq l limit 10select st_astext(st_transform(l.shape, 3857)) from sde_wf_cyyq l limit 103、st_aste…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...