【leetcode刷题之路】剑指Offer(4)——分治+排序算法+动态规划
文章目录
- 8 分治算法
- 8.1 【递归】剑指 Offer 07 - 重建二叉树
- 8.2 【递归】【快速幂】剑指 Offer 16 - 数值的整数次方
- 8.3 【递归】剑指 Offer 33 - 二叉搜索树的后序遍历序列
- 8.4 【递归】【分治】剑指 Offer 17 - 打印从1到最大的n位数
- 8.5 【归并排序】【分治】剑指 Offer 51 - 数组中的逆序对
- 9 排序
- 9.1 【冒泡排序】剑指 Offer 45 - 把数组排成最小的数
- 9.2 【排序】剑指 Offer 61 - 扑克牌中的顺子
- 9.3 【堆排序】剑指 Offer 40 - 最小的k个数
- 9.4 【堆排序】【优先队列】剑指 Offer 41 - 数据流中的中位数
- 10 动态规划
- 10.1 【动态规划】【哈希表】【DFS】剑指 Offer 10- I - 斐波那契数列
- 10.2 【动态规划】【哈希表】【DFS】剑指 Offer 10- II - 青蛙跳台阶问题
- 10.3 【动态规划】剑指 Offer 63 - 股票的最大利润
- 10.4 【动态规划】【分治】剑指 Offer 42 - 连续子数组的最大和
- 10.5 【动态规划】剑指 Offer 47 - 礼物的最大价值
8 分治算法
8.1 【递归】剑指 Offer 07 - 重建二叉树
https://leetcode.cn/problems/zhong-jian-er-cha-shu-lcof/
前序遍历是根左右,中序遍历是左根右,这也就意味着前序遍历的第一个节点是整棵树的根节点,顺着这个节点找到它在中序遍历中的位置,即为in_root,那么in_root左边的都在左子树,右边的都在右子树,这样就可以知道左子树一共有多少个节点,然后去前序遍历中找到左右子树的分界点,分成左右两部分,分别重复上述过程,找到各自部分的第一个根节点,然后再依次往下进行,直到最后左右子树的边界发生重合,此时二叉树重建完毕。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
private:unordered_map<int,int> hash_table;
public:TreeNode* subTree(vector<int>& preorder, vector<int>& inorder, int pre_l, int pre_r, int in_l, int in_r){if(pre_l > pre_r) return nullptr;//找到根节点,计算左子树的节点数int pre_root = pre_l;int in_root = hash_table[preorder[pre_l]];int sub_l = in_root - in_l;//开始生成rootTreeNode* root = new TreeNode(preorder[pre_l]);//对于左子树而言,前序遍历的[左边界+1,左边界+左子树节点数]即为中序遍历的[左边界,根节点-1]root->left = subTree(preorder, inorder, pre_l+1, pre_l+sub_l, in_l, in_root-1);//对于右子树而言,前序遍历的[左边界+左子树节点数+1,右边界]即为中序遍历的[根节点+1,右边界]root->right = subTree(preorder, inorder, pre_l+sub_l+1, pre_r, in_root+1, in_r);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int n = inorder.size();for(int i=0;i<n;i++){hash_table[inorder[i]] = i;}return subTree(preorder, inorder, 0, n-1, 0, n-1);}
};
8.2 【递归】【快速幂】剑指 Offer 16 - 数值的整数次方
https://leetcode.cn/problems/shu-zhi-de-zheng-shu-ci-fang-lcof/description/
这道题可以用快速幂来解决,具体思路就是把幂次按照二进制拆开,分别计算,下面举个例子: 假设我要计算 x 10 x^{10} x10,因为10的二进制表示为1010,那么 x 10 = x 2 0 ∗ 0 ∗ x 2 1 ∗ 1 ∗ x 2 2 ∗ 0 ∗ x 2 3 ∗ 1 x^{10}=x^{2^0*0}*x^{2^1*1}*x^{2^2*0}*x^{2^3*1} x10=x20∗0∗x21∗1∗x22∗0∗x23∗1,可以看作按照x的2次方依次递增,只需要看这一个次方对应的二进制是否为1。
class Solution {
public:double myPow(double x, int n) {if(x==1 || n==0) return 1;if(x==0) return 0;double ans = 1;long num = n;if(n<0){num = -num;x = 1/x;}while(num){if(num & 1) ans *= x;x *= x;num >>= 1;}return ans;}
};
8.3 【递归】剑指 Offer 33 - 二叉搜索树的后序遍历序列
https://leetcode.cn/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof
后序遍历的特点就是先访问左子树再访问右子树最后访问根节点,所以最后一个元素一定根节点,而二叉搜索树的特点就是左子树<根节点<右子树,所以我们可以根据根节点的值把数组分为两部分,然后分别判断是否符合二叉搜索树的特点,重复上述过程直到所有情况都判断完为止。
class Solution {
public:bool dfs(vector<int>& postorder, int left, int right){if(left >= right) return true;int i = left;while(postorder[i]<postorder[right]){i++;}int mid = i;while(postorder[i]>postorder[right]){i++;}return i==right & dfs(postorder,left,mid-1) & dfs(postorder,mid,right-1);}bool verifyPostorder(vector<int>& postorder){return dfs(postorder,0,postorder.size()-1);}
};
8.4 【递归】【分治】剑指 Offer 17 - 打印从1到最大的n位数
https://leetcode.cn/problems/da-yin-cong-1dao-zui-da-de-nwei-shu-lcof
这道题目由于指定了数组是int型,所以不用考虑大整数问题,直接暴力就可以解决,但如果是大整数的话,需要采用分治递归的思想,主要如下:
(1)第一层遍历,为n,分别考虑到生成的数字是1位数、2位数、3位数…n位数;
(2)第二层遍历,分别遍历每一位数是几,除了第一位是1-9之外,其余都是0-9。
class Solution {
public:vector<int> printNumbers(int n) {int cnt = pow(10,n);vector<int> ans;for(int i=1;i<cnt;i++){ans.push_back(i);}return ans;}
};
8.5 【归并排序】【分治】剑指 Offer 51 - 数组中的逆序对
https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof
这位大佬写的很好!(https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solutions/622496/jian-zhi-offer-51-shu-zu-zhong-de-ni-xu-pvn2h)
class Solution {
public:int merge_sort(int left, int right, vector<int>& nums, vector<int>& tmp){if(left >= right) return 0;int mid = (left + right) / 2;int res = merge_sort(left, mid, nums, tmp) + merge_sort(mid+1, right, nums, tmp);int i = left, j = mid + 1;for(int k=left;k<=right;k++){tmp[k] = nums[k];}for(int k=left;k<=right;k++){ if(i == mid+1) nums[k] = tmp[j++];else if(j == right+1 || tmp[i] <= tmp[j]) nums[k] = tmp[i++];else{nums[k] = tmp[j++];res += mid - i + 1;}}return res;}int reversePairs(vector<int>& nums){vector<int> tmp(nums.size());return merge_sort(0, nums.size()-1, nums, tmp);}
};
9 排序
9.1 【冒泡排序】剑指 Offer 45 - 把数组排成最小的数
https://leetcode.cn/problems/ba-shu-zu-pai-cheng-zui-xiao-de-shu-lcof
这题可以看作是冒泡排序,只不过针对的对象是字符串,我们需要找到里面表示最大的字符串,然后把它放到字符串的最后即可,例如“32”和“3”,因为“323”<“332”,所以“32”<“3”,所以应该把“3”放在“32”后面,借助这种排序思路来解题。
class Solution {
public:string minNumber(vector<int>& nums) {for(int i=nums.size()-1;i>0;i--){for(int j=0;j<i;j++){if(string_sort(nums[j],nums[j+1])){swap(nums[j],nums[j+1]);}}}string ans = "";for(int i=0;i<nums.size();i++){ans += to_string(nums[i]);}return ans;}bool string_sort(int num1, int num2){string s1 = to_string(num1) + to_string(num2);string s2 = to_string(num2) + to_string(num1);if(s1>s2) return true;else return false;}
};
9.2 【排序】剑指 Offer 61 - 扑克牌中的顺子
https://leetcode.cn/problems/bu-ke-pai-zhong-de-shun-zi-lcof
这道题不难,想清楚顺子的判断条件即可,主要为以下几个方面:
(1)五个数中除了0以外不能有其他的重复数字,否则肯定不是顺子;
(2)找出五个数中的最大值和最小值,看看这两个数之间缺的数的个数是多少,记为gap,然后计算五个数中0的个数,记为zero_num,如果gap<=zero_num,说明0的个数可以补全缺的数,否则就肯定不是顺子。
class Solution {
public:bool isStraight(vector<int>& nums) {int arr[14] = {0};int max_num = 0, min_num = 14, zero_num = 0;for(int i=0;i<5;i++){if(nums[i]==0) zero_num++;else{if(arr[nums[i]]) return false;else{arr[nums[i]] = 1;min_num = min(min_num, nums[i]);max_num = max(max_num, nums[i]);}}}int gap = 0;for(int i=min_num;i<max_num;i++){if(arr[i]!=1) gap++;}if(gap <= zero_num) return true;else return false;}
};
9.3 【堆排序】剑指 Offer 40 - 最小的k个数
https://leetcode.cn/problems/zui-xiao-de-kge-shu-lcof
方法一:直接用sort排序,然后选前k个数就好了。
方法二:用堆排序,堆排序,采用大根堆,首先把前k个数字存入大根堆中,之后的数字依次和大根堆的top比较,如果比top小就更新大根堆,最后把大根堆中的数字存入vector中作为答案返回。
//方法一:直接排序
class Solution {
public:vector<int> getLeastNumbers(vector<int>& arr, int k) {sort(arr.begin(),arr.end());vector<int> ans;for(int i=0;i<k;i++){ans.push_back(arr[i]);}return ans;}
};
//方法二:堆排序
class Solution {
public:vector<int> getLeastNumbers(vector<int>& arr, int k) {vector<int> ans;if(k == 0) return ans;priority_queue<int, vector<int>, less<int>> max_stack;//把前k个数字存入大根堆for(int i=0;i<k;i++){max_stack.push(arr[i]);}//依次和大根堆的top比较,如果比top小就更新大根堆for(int j=k;j<arr.size();j++){if(arr[j] < max_stack.top()){max_stack.pop();max_stack.push(arr[j]);}}//把大根堆中的数字存入vector中作为答案返回while(k--){ans.push_back(max_stack.top());max_stack.pop();}return ans;}
};
9.4 【堆排序】【优先队列】剑指 Offer 41 - 数据流中的中位数
https://leetcode.cn/problems/shu-ju-liu-zhong-de-zhong-wei-shu-lcof
这道题如果直接对所有数进行排序的话,最后会runtime,其实只要能找出每一次执行findMedian函数时整个数据流中间的两个数或者一个数就行了,这是我们可以考虑用堆排序,同时维持一个大根堆和一个小根堆,把数据流中的数分为两部分,同时也要保证大根堆中的top要比小根堆中的top小,这样最后的中位数要么是小根堆top,要么就是大根堆和小根堆的top取平均,构造方法如下:
- 如果大根堆和小根堆的size一样,那么此时add的num就加入大根堆,然后把大根堆的top插入到小根堆中,保证大根堆的size<=小根堆的size;
- 如果大根堆和小根堆的size不一样,那么此时add的num就加入小根堆,然后把小根堆的top插入到大根堆中,保证小根堆的size<=大根堆的size;
- 执行findMedian函数时,看看此时大根堆和小根堆的size是否相等,如果相等的话,中位数就是各自取top元素相加取平均,如果不相等,那么中位数就是小根堆的top。
class MedianFinder {
public:/** initialize your data structure here. */priority_queue<int, vector<int>, greater<int>> min_stack;priority_queue<int, vector<int>, less<int>> max_stack;MedianFinder() {}void addNum(int num) {//如果大根堆和小根堆的size一样,那么此时add的num就加入大根堆,然后把大根堆的top插入到小根堆中,保证大根堆的size<=小根堆的sizeif(min_stack.size() == max_stack.size()){max_stack.push(num);min_stack.push(max_stack.top());max_stack.pop();}//如果大根堆和小根堆的size不一样,那么此时add的num就加入小根堆,然后把小根堆的top插入到大根堆中,保证小根堆的size<=大根堆的sizeelse{min_stack.push(num);max_stack.push(min_stack.top());min_stack.pop();}}//执行findMedian函数时,看看此时大根堆和小根堆的size是否相等,如果相等的话,中位数就是各自取top元素相加取平均,如果不相等,那么中位数就是小根堆的topdouble findMedian() {if(min_stack.size() == max_stack.size()){return (max_stack.top() + min_stack.top()) / 2.0;}else return min_stack.top();}
};/*** Your MedianFinder object will be instantiated and called as such:* MedianFinder* obj = new MedianFinder();* obj->addNum(num);* double param_2 = obj->findMedian();*/
10 动态规划
10.1 【动态规划】【哈希表】【DFS】剑指 Offer 10- I - 斐波那契数列
https://leetcode.cn/problems/fei-bo-na-qi-shu-lie-lcof
这道题如果直接用动态规划会runtime,主要是因为在计算过程中会有一些数被反复计算,所以我们在这里采用哈希表来存放已经被计算过的数,这样在之后再次被计算时直接用就好了。
class Solution {
public:unordered_map<int,int> hash_table;int dfs(int n){if(n == 0) return 0;else if(n == 1) return 1;else{if(hash_table.count(n)) return hash_table[n];else{int num1 = dfs(n-1) % 1000000007;int num2 = dfs(n-2) % 1000000007;hash_table[n] = (num1 + num2) % 1000000007;return hash_table[n];}}}int fib(int n) {return dfs(n);}
};
10.2 【动态规划】【哈希表】【DFS】剑指 Offer 10- II - 青蛙跳台阶问题
https://leetcode.cn/problems/qing-wa-tiao-tai-jie-wen-ti-lcof
这道题目就是变形的斐波那契数列,在这里采用哈希表来存放已经被计算过的数,这样在之后再次被计算时直接用就好了。
class Solution {
public:unordered_map<int,int> hash_table;int dfs(int n){if(n == 0) return 1;else if(n == 1) return 1;else{if(hash_table.count(n)) return hash_table[n];else{int num1 = dfs(n-1) % 1000000007;int num2 = dfs(n-2) % 1000000007;hash_table[n] = (num1 + num2) % 1000000007;return hash_table[n];}}}int numWays(int n) {return dfs(n);}
};
10.3 【动态规划】剑指 Offer 63 - 股票的最大利润
https://leetcode.cn/problems/gu-piao-de-zui-da-li-run-lcof
动态规划类题目的解题主要是找到状态转移方程就好了,对于这道题目的状态转移就在于某一天有无股票,我们以此为分界来定义状态转移方程dp[i][2]:
(1)前i天未持有股票
d p [ i ] [ 0 ] = m a x ( d p [ i − 1 ] [ 0 ] , d p [ i − 1 ] [ 1 ] + p r i c e s [ i ] ) dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]) dp[i][0]=max(dp[i−1][0],dp[i−1][1]+prices[i])
(2)前i天持有股票
d p [ i ] [ 1 ] = m a x ( d p [ i − 1 ] [ 1 ] , 0 − p r i c e s [ i ] ) dp[i][1] = max(dp[i-1][1], 0 - prices[i]) dp[i][1]=max(dp[i−1][1],0−prices[i])
同时还要预判一下prices为空的情况,此时返回0,因为dp的两个元素在反复调用,所以在代码中也是直接用两个变量来进行代替了。
class Solution {
public:int maxProfit(vector<int>& prices) {if(!prices.size()) return 0;int dp_0 = 0, dp_1 = -prices[0];for(int i=1;i<prices.size();i++){dp_0 = max(dp_0, dp_1 + prices[i]);dp_1 = max(dp_1, 0 - prices[i]);}return dp_0;}
};
10.4 【动态规划】【分治】剑指 Offer 42 - 连续子数组的最大和
https://leetcode.cn/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof
这道题用到一点点分治的思想,假设现在数组长度为 n n n,连续子数组的最大和为 f ( n ) f(n) f(n),那么 f ( n ) = m a x ( f ( n − 1 ) + n u m s [ i ] , n u m [ i ] ) f(n)=max(f(n-1)+nums[i],num[i]) f(n)=max(f(n−1)+nums[i],num[i]),也就意味着最大和要么是前 n − 1 n-1 n−1个数的最大和加上第 i i i个数,要么就是第 i i i个数本身,如果是第 i i i个数本身的话,就要从这里开始重新找到连续子数组了,在这个过程中记录下最大值即可。
class Solution {
public:int maxSubArray(vector<int>& nums) {int pre = 0, max_seqsum = nums[0];for(int i=0;i<nums.size();i++){pre = max(pre + nums[i], nums[i]);max_seqsum = max(max_seqsum, pre);}return max_seqsum;}
};
10.5 【动态规划】剑指 Offer 47 - 礼物的最大价值
https://leetcode.cn/problems/li-wu-de-zui-da-jie-zhi-lcof
其实每个地方的最大值只与两个状态有关,假设目前要求的是 v a l u e [ i ] [ j ] value[i][j] value[i][j]的最大值,那么 v a l u e [ i ] [ j ] = m a x ( v a l u e [ i ] [ j − 1 ] , v a l u e [ i − 1 ] [ j ] ) + g r i d [ i ] [ j ] value[i][j] = max(value[i][j-1],value[i-1][j]) + grid[i][j] value[i][j]=max(value[i][j−1],value[i−1][j])+grid[i][j],这里为了方便初始化,把初始数组的大小设置为 ( m + 1 ) ∗ ( n + 1 ) (m+1)*(n+1) (m+1)∗(n+1)。
class Solution {
public:int maxValue(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();int value[m+1][n+1];memset(value,0,sizeof(value));for(int i=0;i<m;i++){for(int j=0;j<n;j++){value[i+1][j+1] = max(value[i+1][j],value[i][j+1]) + grid[i][j];}}return value[m][n];}
};
相关文章:
——分治+排序算法+动态规划)
【leetcode刷题之路】剑指Offer(4)——分治+排序算法+动态规划
文章目录 8 分治算法8.1 【递归】剑指 Offer 07 - 重建二叉树8.2 【递归】【快速幂】剑指 Offer 16 - 数值的整数次方8.3 【递归】剑指 Offer 33 - 二叉搜索树的后序遍历序列8.4 【递归】【分治】剑指 Offer 17 - 打印从1到最大的n位数8.5 【归并排序】【分治】剑指 Offer 51 -…...

美创科技“签”手柠檬文才学堂,共推高校数据安全建设
近日,由柠檬文才学堂联合中国教育在线、东北财经大学网络教育学院共同主办的“三教统筹下高校继续教育数字化转型研讨”顺利召开。 国内高等院校(高职院校)继续教育分管领导,继续教育学院领导及继续教育信息化、教学教务管理、课程…...
【JAVA基础】数据类型,逻辑控制
❤️ Author: 老九 ☕️ 个人博客:老九的CSDN博客 🙏 个人名言:不可控之事 乐观面对 😍 系列专栏: 文章目录 数据类型整型变量 int长整型变量 long单精度浮点数 float双精度浮点数 double字符类型 char字节…...
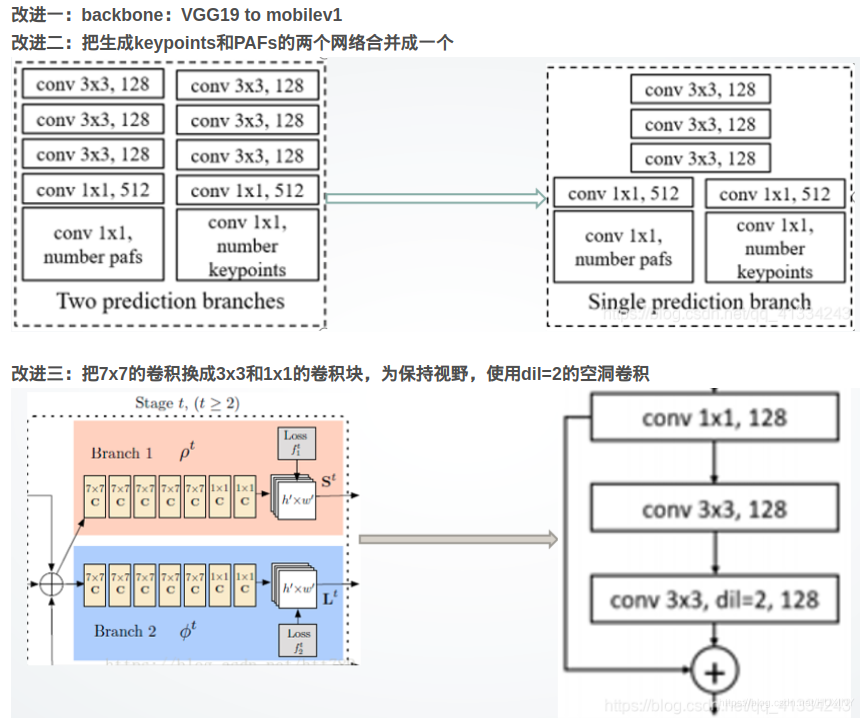
计算机竞赛 基于图像识别的跌倒检测算法
前言 🔥 优质竞赛项目系列,今天要分享的是 基于图像识别的跌倒检测算法 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-senior/…...
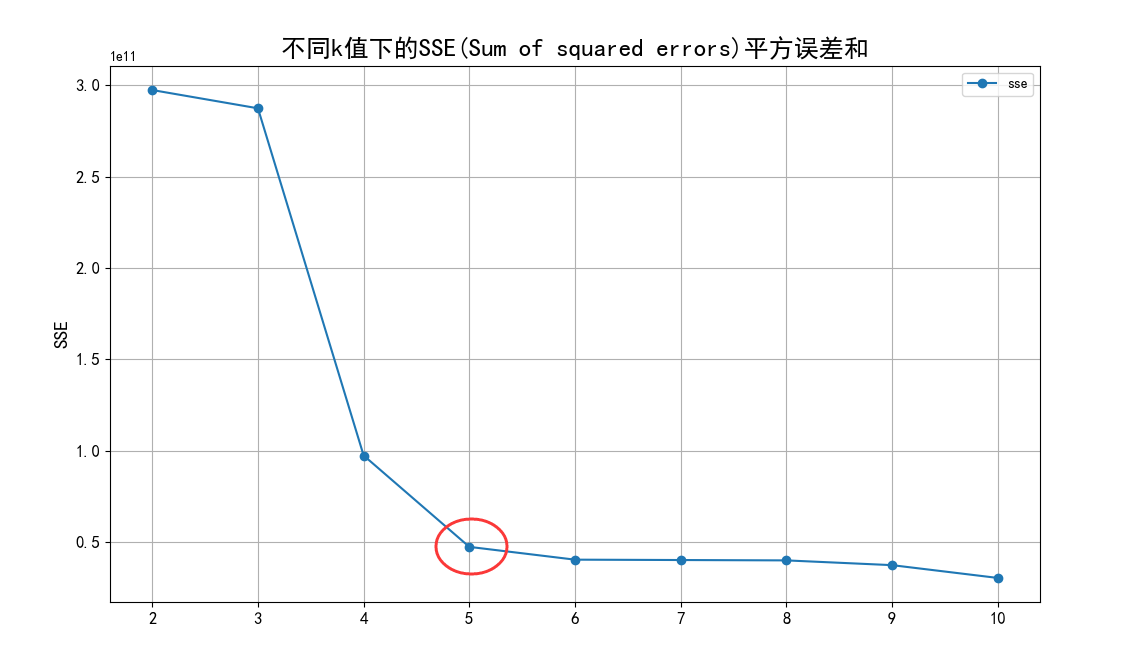
计算机竞赛 基于大数据的股票量化分析与股价预测系统
文章目录 0 前言1 课题背景2 实现效果3 设计原理QTChartsarma模型预测K-means聚类算法算法实现关键问题说明 4 部分核心代码5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于大数据的股票量化分析与股价预测系统 该项目较为新颖…...

input子系统
内核分三层 1、事件处理层 2、核心层 3、设备驱动层 当硬件按下,在设备驱动中触发中断,中断程序会将事件上报给核心层 核心层将事件给事件处理层,最后事件处理层控制app应用层的怎么操作将数据发送到用户空间...

mac 10.13.6安装后开发准备工作
git下载安装 xcode旧版安装搜索 brew国内源安装 brew国内源安装地址2 brew更换源 SwitchHosts github hosts nfts磁盘读写工具 更新ssl证书 证书下载 然后备份一下系统原来的pem文件 cp /etc/ssl/cert.pem /etc/ssl/cert.bak.pem 之后将新下载的pem文件,拷贝到/etc…...

C++ using关键字
C using关键字 using关键字用来简化代码和提高可读性。 using关键字提供了一种灵活的方式,可以在C中导入命名空间和定义别名。 1. 导入命名空间 using namespace 可以将一个命名空间中的所有名称导入到当前作用域中,从而可以直接使用该命名空间中的所…...

让你对es有一个初步的了解
首先es在海量数据的搜索能力非常好,es你可以把他看成一个搜索引擎数据库,他是个非关系型数据库。他的语法有很大的不同,好像都是json风格的。还有一点需要说的就是es 的数据是存在硬盘上的, 我们先来看一下mysql和es的区别吧。一…...
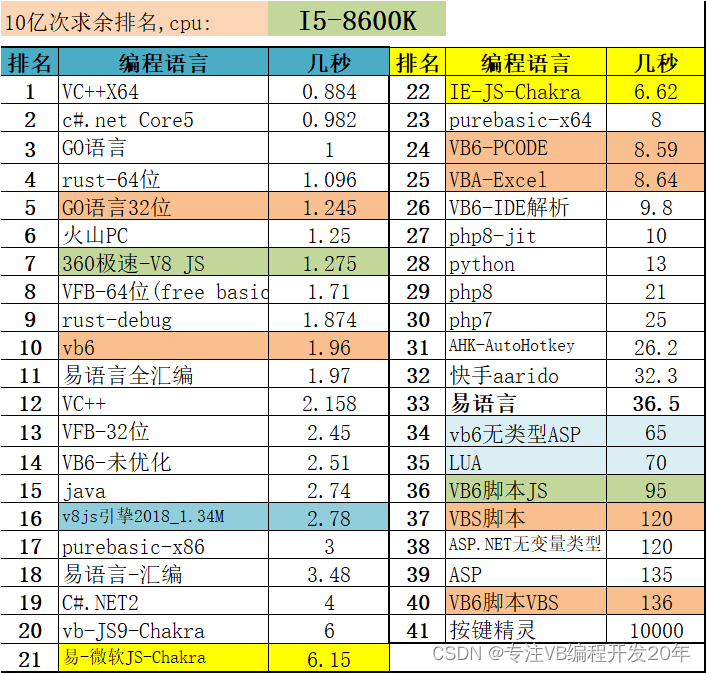
编绎和优化,脚本代码小米加步枪赶超英法美
编程达人:冰冻牡蛎 测试,总结》》 今有空,继续看了一下竹笋大师几天前提出的“使用for循环查找10亿内可被7整除的数的个数”的题目(相关文件:群文件 10亿以内多少个数字可以整除7.7z ) 1. 论输出的exe大小…...
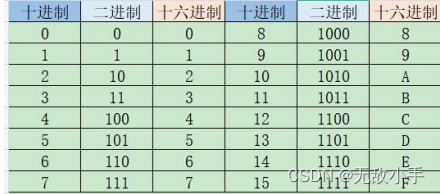
数字电路-二进制学习
什么是二进制? 数字电路 中 只有 高电平 和低电平 就是 1 和0 进位规则是“逢二进一”,借位规则是“借一当二”。 二进制、八进制 、十进制、十六进制 二进制 有两个数来表示 : 0、1 八进制 有8个数来表示 : 0、1、2、3、4、…...

运维Shell脚本小试牛刀(一)
运维Shell脚本小试牛刀(一) 运维Shell脚本小试牛刀(二) 一: Shell中循环剖析 for 循环....... #!/bin/bash - # # # # FILE: countloop.sh # USAGE: ./countloop.sh # DESCRIPTION: # OPTIONS: ------- # …...

screen命令,可以断开服务器连接,依旧能运行你的程序了
可以参考博客1:https://blog.csdn.net/nima_zhang_b/article/details/82797928 可以参考博客2:https://blog.csdn.net/herocheney/article/details/130984403 Linux中的screen是一个命令行工具,可以让用户在同一个终端会话中创建多个虚拟终端。它非常有…...
【ArcGIS Pro二次开发】(63):批量更改字段别名
在我工作中遇到的大多数图斑,字段名称一般是英文,字段别名是中文,使用起来是比较方便的。 但有时候也会遇到一些不一样的情况,不知是经过了怎样的处理,图斑的字段别名被修改成了和字段名称一样的英文,这样…...

redis全套参数配置及降级解决方案
文章目录 redis高可用核心参数配置1.Lettuce2.Jedis3.Redisson4.其他客户端 redis降级场景简介一、业务背景二、设计方案三、实现方案四、总结 redis高可用核心参数配置 1.Lettuce 提示:该客户端无主动探活机制,只能依赖于 OS KeepaAlive 机制…...

AMD即将上市大量中端显卡,为新显卡支付过高价格的日子可能结束
AMD在本周末(8月25日)的德国Gamescom活动中展示了两款新显卡和一些新的升级技术,这些新GPU的定价将与英伟达的GeForce RTX 4000卡竞争。 这是一件大事,因为新的Radeon RX 7700 XT和7800 XT卡占据了AMD Radeon RX 7000系列产品线…...

go学习一之go的初体验
go语言学习笔记 一、golang初体验: 1.简单体验案例: package main{ //把这个test.go归属到main import "fmt" //引入一个包 func main(){//输出hellofmt.Println("hello world")} }2.从案例学到的知识点: (1) go文件的后缀是.…...

智能制造产业链数字化转型、数字化互联工厂建设方案PPT
本资料来源公开网络,仅供个人学习,请勿商用,如有侵权请联系删除,更多浏览公众号:智慧方案文库 篇幅有限,无法完全展示,喜欢资料可转发评论,私信了解更多信息。...

【安卓】拿注册码的两种方式
【安卓】拿注册码的两种方式 文章仅用于学习交流,请勿利用文章中的技术对任何计算机系统进行入侵操作。利用此文所提供的信息而造成的直接或间接后果和损失,均由使用者本人负责。首发吾爱:https://www.52pojie.cn/thread-1826802-1-1.html言归…...
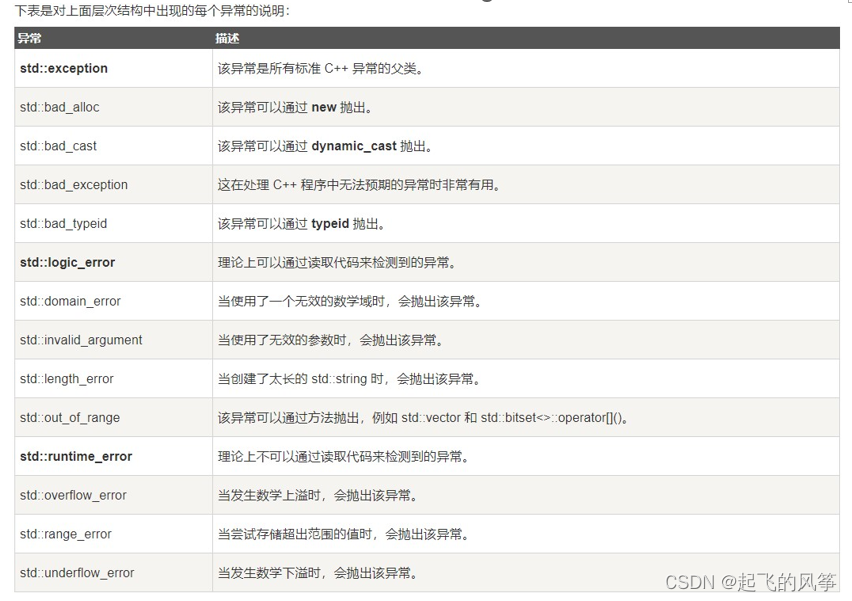
【C++】—— 异常处理
前言: 本期,我将给大家讲解的是有关 异常处理 的相关知识! 目录 (一)C语言传统的处理错误的方式 (二)C异常概念 (三)异常的使用 1、异常的抛出和捕获 1️⃣ 异常的…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
