K-Means(K-均值)聚类算法理论和实战
目录
K-Means 算法
K-Means 术语
K 值如何确定
K-Means 场景
美国总统大选摇争取摆选民
电商平台用户分层
给亚洲球队做聚类
编辑
其他场景
K-Means 工作流程
K-Means 开发流程
K-Means的底层代码实现
K-Means 的评价标准
K-Means 算法
对于 n 个样本点来说,根据距离公式(如欧式距离)去计 算它们的远近,距离越近越相似。按照这样的规则,我们把它们划分到 K 个类别中,让每个类别中的样本点都是最相似的。
优点:
属于无监督学习,无须准备训练集
原理简单,实现起来较为容易
结果可解释性较好
缺点:
需手动设置k值。 在算法开始预测之前,我们需要手动设置k值,即估计数据大概的类别个数,不合理的k值会使结果缺乏解释性
可能收敛到局部最小值, 在大规模数据集上收敛较慢
对于异常点、离群点敏感
使用数据类型 : 数值型数据
K-Means 术语
簇: 所有数据的点集合,簇中的对象是相似的。
质心: 簇中所有点的中心(计算所有点的均值而来).
SSE: Sum of Sqared Error(误差平方和), 它被用来评估模型的好坏,SSE 值越小,表示越接近它们的质心. 聚类效果越好。由于对误差取了平方,因此更加注重那些远离中心的点(一般为边界点或离群点)。
K 值如何确定
K-means 的算法原理我们就解释完了,但还有一个问题没有解决,那就是我们怎么知道数据
需要分成几个类别,也就是怎么确定 K 值呢?K 值的确定,一般来说要取决于个人的经验和感觉,没有一个统一的标准。所以,要确定 K 值 是一项比较费时费力的事情,最差的办法是去循环尝试每一个 K 值。然后,在不同的 K 值情 况下,通过每一个待测样本点到质心的距离之和,来计算平均距离。
K-Means 场景
美国总统大选摇争取摆选民
kmeans,如前所述,用于数据集内种类属性不明晰,希望能够通过数据挖掘出或自动归类出有相似特点的对象的场景。其商业界的应用场景一般为挖掘出具有相似特点的潜在客户群体以便公司能够重点研究、对症下药。
例如,在2000年和2004年的美国总统大选中,候选人的得票数比较接近或者说非常接近。任一候选人得到的普选票数的最大百分比为50.7%而最小百分比为47.9% 如果1%的选民将手中的选票投向另外的候选人,那么选举结果就会截然不同。 实际上,如果妥善加以引导与吸引,少部分选民就会转换立场。尽管这类选举者占的比例较低,但当候选人的选票接近时,这些人的立场无疑会对选举结果产生非常大的影响。如何找出这类选民,以及如何在有限的预算下采取措施来吸引他们? 答案就是聚类(Clustering)。
那么,具体如何实施呢?首先,收集用户的信息,可以同时收集用户满意或不满意的信息,这是因为任何对用户重要的内容都可能影响用户的投票结果。然后,将这些信息输入到某个聚类算法中。接着,对聚类结果中的每一个簇(最好选择最大簇 ), 精心构造能够吸引该簇选民的消息。最后, 开展竞选活动并观察上述做法是否有效。
另一个例子就是产品部门的市场调研了。为了更好的了解自己的用户,产品部门可以采用聚类的方法得到不同特征的用户群体,然后针对不同的用户群体可以对症下药,为他们提供更加精准有效的服务。
电商平台用户分层
电商平台的运营工作经常需要对用户进行分层,针对不同层次的用户采取不同的运营策略,这个过程也叫做精细化运营。
就我知道的情况来说,运营同学经常会按照自己的经验,比如按照用户的下单次数,或者按照
用户的消费金额,通过制定的一些分类规则给用户进行分层,如下表格,我们就可以得到三种
不同价值的用户。
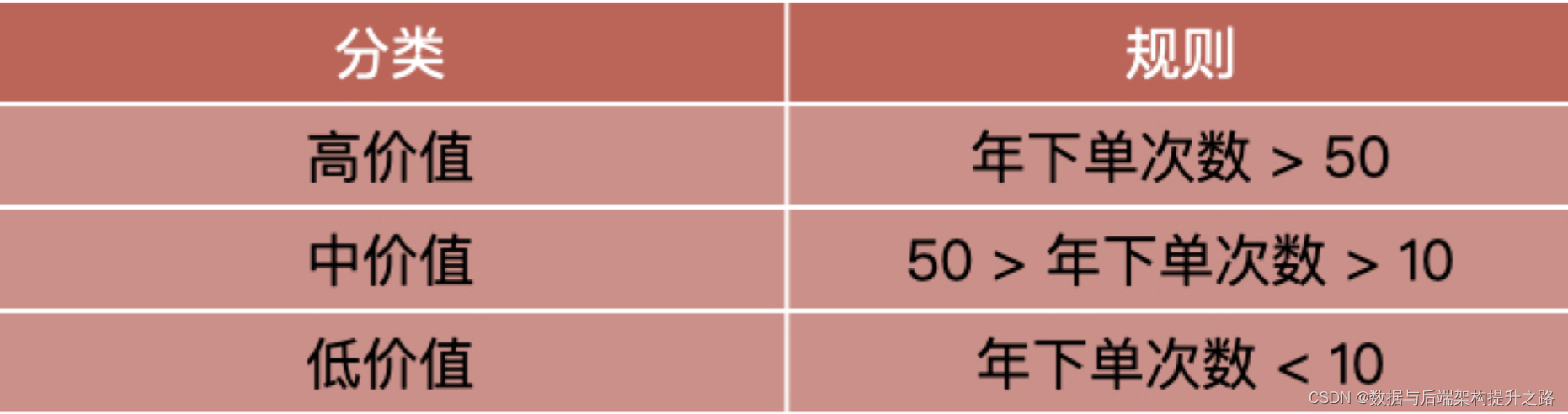
这种划分的方法简单来看是没有大问题的,但是并不科学。为什么这么说呢?这主要有两方面原因。
一方面,只用单一的“下单次数”来衡量用户的价值度并不合理,因为用户下单的品类价格不同,很可能会出现的情况是,用户 A 多次下单的金额给平台带来的累计 GMV(网站的成交金额) ,还不如用户 B 的一次下单带来的多。因此,只通过“下单次数”来衡量用户价值就不合理。因为一般来说,我们会结合下单次数、消费金额、活跃程度等等很多的指标进行综合分析。
另一方面,就算我们可以用单一的“下单次数”进行划分用户,但是不同人划分的标准不一样,“下单次数”的阈值需要根据数据分析求出来,直接用 10 和 50 就不合理。这两方面原因,就会导致我们分析出来的用户对平台的贡献度差别特别大。因此,我们需要用一种科学的、通用的划分方法去做用户分群
RFM 作为用户价值划分的经典模型,就可以解决这种分群的问题,RFM 是客户分析及衡量客户价值的重要模型之一。其中 ,R 表示最近一次消费(Recency),F 表示消费频率 (Frequency),M 表示消费金额(Monetary)。

我们可以将每个维度分为高低两种情况,如 R 的高低、F 的高低,以及 M 的高低,构建出一 个三维的坐标系。
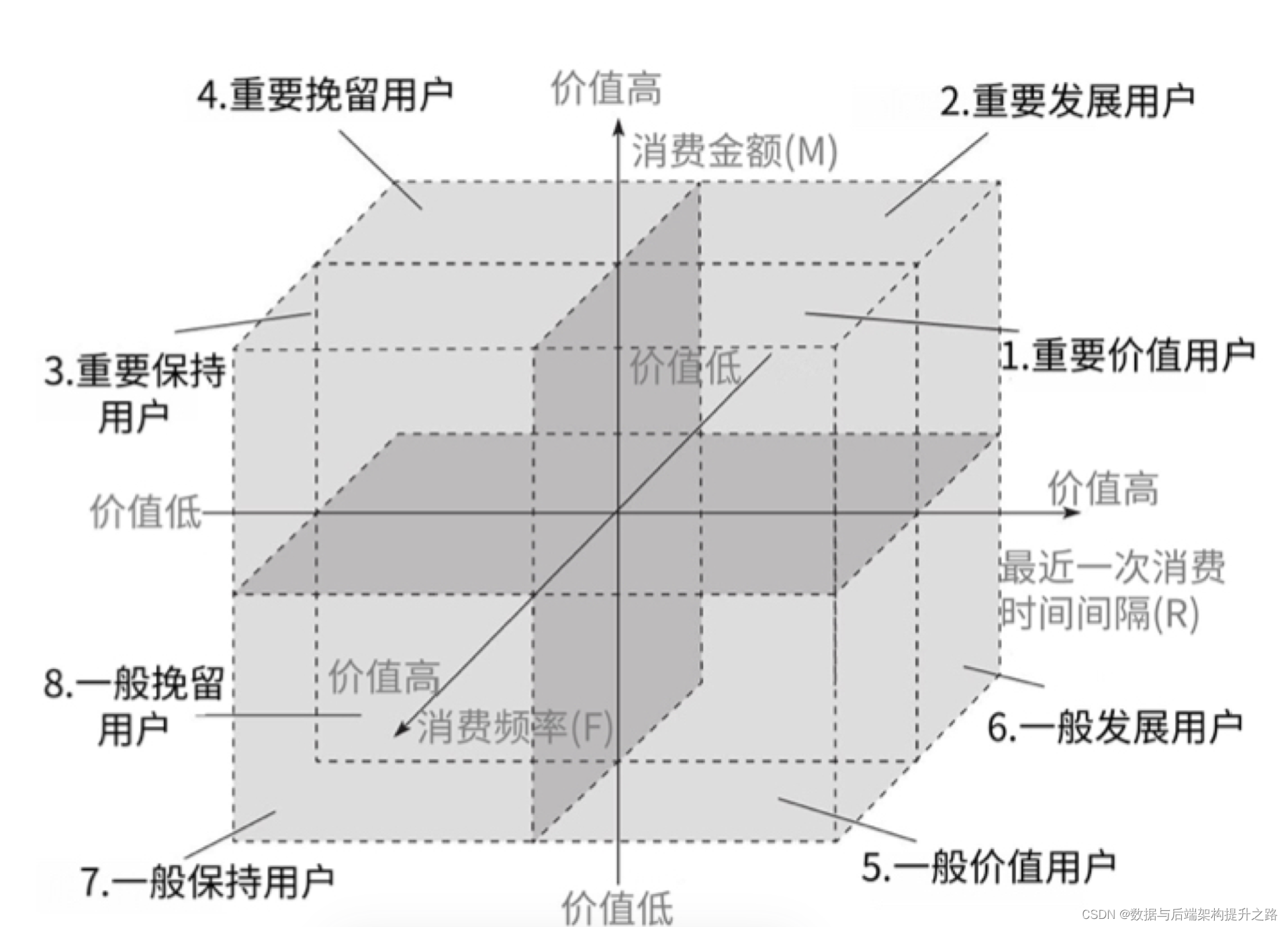

然后,我们通过用户历史数据(如订单数据、浏览日志),统计出每个用户的 RFM 数据USERPIN:用户唯一 ID;
R:最后一次消费日期距现在的时间,例如最后消费时间到现在距离 5 天,则 R 就是 5;
F:消费频率,例如待统计的一段时间内用户消费了 20 次,则 F 就是 20;
M:消费金额,例如待统计的一段时间内用户累计消费了 1000 元钱,则 M 就是 1000
这样,我们就有了 8000 个样本数据,每个样本数据包含三个特征,分别为 R、F,M,然后根据前面 RFM 分为 8 个用户群体,则意味着 K 值为 8。
最后,我们将数据代入到 K-means 算法,K-means 将按照本节课讲解的计算逻辑进行计算,最终将 8000 个样本数据聚类成 8 个用户群体。这个时候,运营同学就可以根据新生成的RFM 用户分群进行针对性的营销策略了。
给亚洲球队做聚类
其中 2019 年国际足联的世界排名,2015 年亚洲杯排名均为实际排名。2018 年世界杯中, 很多球队没有进入到决赛圈,所以只有进入到决赛圈的球队才有实际的排名。如果是亚洲区预 选赛 12 强的球队,排名会设置为 40。如果没有进入亚洲区预选赛 12 强,球队排名会设置为50。
针对上面的排名,我们首先需要做的是数据规范化。你可以把这些值划分到[0,1]或者按照均值为 0,方差为 1 的正态分布进行规范化。具体数据规范化的步骤可以看下 13 篇,也就是数据变换那一篇。我先把数值都规范化到[0,1]的空间中,得到了以下的数值表:

计算每个队伍分别到中国、日本、韩国的欧氏距离,然后根据距离远近来划分。我们看到大部分的队,会和中国队聚 类到一起。这里我整理了距离的计算过程,比如中国和中国的欧氏距离为 0,中国和日本的欧氏距离为 0.732003。如果按照中国、日本、韩国为 3 个分类的中心点,欧氏距离的计算结果如下表所示:

然后我们再重新计算这三个类的中心点,如何计算呢?最简单的方式就是取平均值,然后根据新的中心点按照距离远近重新分配球队的分类,再根据球队的分类更新中心点的位置。计算过程这里不展开,最后一直迭代(重复上述的计算过程:计算中心点和划分分类)到分类不再发生变化,可以得到以下的分类结果:
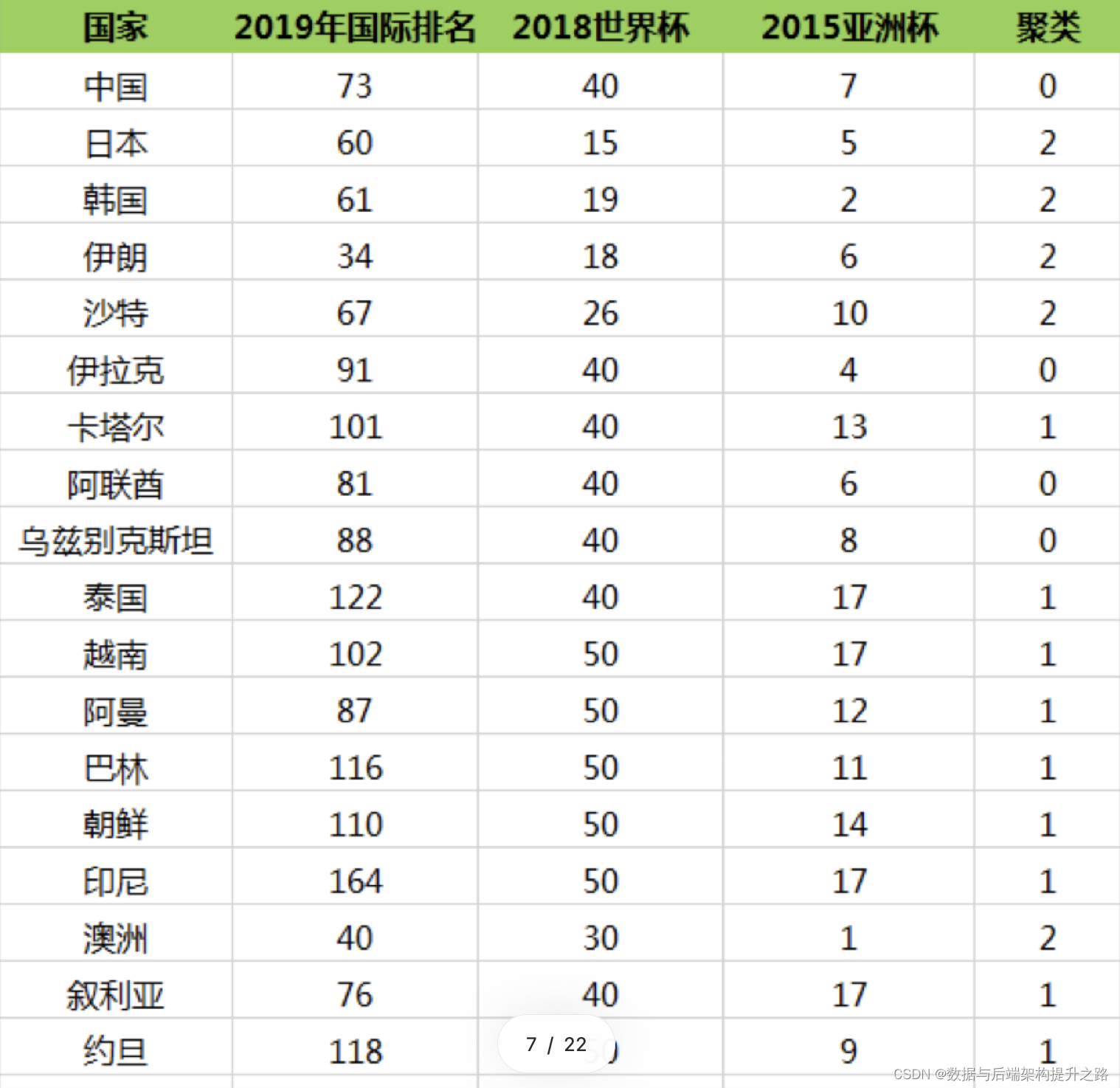
所以我们能看出来第一梯队有日本、韩国、伊朗、沙特、澳洲;第二梯队有中国、伊拉克、阿联酋、乌兹别克斯坦;第三梯队有卡塔尔、泰国、越南、阿曼、巴林、朝鲜、印尼、叙利亚、约旦、科威特和巴勒斯坦。
# coding: utf-8
from sklearn.cluster import KMeans
from sklearn import preprocessing
import pandas as pd
# 输入数据
data = pd.read_csv('data.csv', encoding='gbk')
train_x = data[["2019年国际排名","2018世界杯","2015亚洲杯"]]
df = pd.DataFrame(train_x)# 我们能看到在 K-Means 类创建的过程中,有一些主要的参数:
# n_clusters: 即 K 值,一般需要多试一些 K 值来保证更好的聚类效果。你可以随机设置一些
# K 值,然后选择聚类效果最好的作为最终的 K 值;# max_iter: 最大迭代次数,如果聚类很难收敛的话,设置最大迭代次数可以让我们及时得
# 到反馈结果,否则程序运行时间会非常长;# n_init:初始化中心点的运算次数,默认是 10。程序是否能快速收敛和中心点的选择关系
# 非常大,所以在中心点选择上多花一些时间,来争取整体时间上的快速收敛还是非常值得
# 的。由于每一次中心点都是随机生成的,这样得到的结果就有好有坏,非常不确定,所以要
# 运行 n_init 次, 取其中最好的作为初始的中心点。如果 K 值比较大的时候,你可以适当增大 n_init 这个值;# init: 即初始值选择的方式,默认是采用优化过的 k-means++ 方式,你也可以自己指定
# 中心点,或者采用 random 完全随机的方式。自己设置中心点一般是对于个性化的数据进
# 行设置,很少采用。random 的方式则是完全随机的方式,一般推荐采用优化过的 k- means++ 方式;# algorithm:k-means 的实现算法,有“auto” “full”“elkan”三种。一般来说建议直
# 接用默认的"auto"。简单说下这三个取值的区别,如果你选择"full"采用的是传统的 K-
# Means 算法,“auto”会根据数据的特点自动选择是选择“full”还是“elkan”。我们一
# 般选择默认的取值,即“auto” 。kmeans = KMeans(n_clusters=3)
# 规范化到[0,1]空间
min_max_scaler=preprocessing.MinMaxScaler()
train_x=min_max_scaler.fit_transform(train_x)
# kmeans算法
kmeans.fit(train_x)
predict_y = kmeans.predict(train_x)
# 合并聚类结果,插入到原数据中
result = pd.concat((data,pd.DataFrame(predict_y)),axis=1)
result.rename({0:u'聚类'},axis=1,inplace=True)
print(result)其他场景
K-means 算 法可以应用场景还有很多,常见的有文本聚类、售前辅助、风险监测等等。下面,我们一一来说。
文本聚类:根据文档内容或主题对文档进行聚类。有些 APP 或小程序做的事儿,就是从网络中爬取文章,然后通过 K-means 算法对文本进行聚类,结构化后最终展示给自己的用户。
售前辅助:根据用户的通话、短信和在线留言等信息,结合用户个人资料,帮助公司在售前对客户做更多的预测。
风险监测:在金融风控场景中,在没有先验知识的情况下,通过无监督方法对用户行为做异常检测。
K-Means 工作流程
第一步,随机选取任意 K 个数据点作为初始质心;
第二步,分别计算数据集中每一个数据点与每一个质心的距离,数据点距离哪个质心最近,就属于哪个聚类;
第三步,在每一个聚类内,分别计算每个数据点到质心的距离,取均值作为下一轮迭代的质心;
第四步,如果新质心和老质心之间的距离不再变化或小于某一个阈值,计算结束。
K-Means 开发流程
收集数据: 使用任意方法
准备数据: 需要数值型数据类计算距离, 也可以将标称型数据映射为二值型数据再用于距离计算
分析数据: 使用任意方法
训练算法: 不适用于无监督学习,即无监督学习不需要训练步骤
测试算法: 应用聚类算法、观察结果.可以使用量化的误差指标如误差平方和(后面会介绍)来评价算法的结果.
使用算法: 可以用于所希望的任何应用.通常情况下, 簇质心可以代表整个簇的数据来做出决策.
K-Means的底层代码实现
# 计算两个向量的欧氏距离
def distEclud(vecA,vecB):return sqrt(sum(power(vecA-vecB,2))# 传入的数据时numpy的矩阵格式
def randCent(dataMat, k):n = shape(dataMat)[1] centroids = mat(zeros((k,n))) for j in range(n):minJ = min(dataMat[:,j]) # 找出矩阵dataMat第j列最小值rangeJ = float(max(dataMat[:,j]) - minJ) #计算第j列最大值和最小值的差 #赋予一个随机质心,它的值在整个数据集的边界之内centroids[:,j] = minJ + rangeJ * random.rand(k,1) return centroids #返回一个随机的质心矩阵#k-均值算法
def kMeans(dataMat,k,distE = distEclud , createCent=randCent): m = shape(dataMat)[0] # 获得行数mclusterAssment = mat(zeros((m,2))) # 初试化一个矩阵,用来记录簇索引和存储误差 centroids = createCent(dataMat,k) # 随机的得到一个质心矩阵蔟clusterChanged = True while clusterChanged:clusterChanged = Falsefor i in range(m): #对每个数据点寻找最近的质心 minDist = inf; minIndex = -1for j in range(k): # 遍历质心蔟,寻找最近的质心distJ1 = distE(centroids[j,:],dataMat[i,:]) #计算数据点和质心的欧式距离 if distJ1 < minDist:minDist = distJ1; minIndex = j if clusterAssment[i,0] != minIndex:clusterChanged = TrueclusterAssment[i,:] = minIndex,minDist**2 print centroidsfor cent in range(k): #更新质心的位置ptsInClust = dataMat[nonzero(clusterAssment[:,0].A==cent)[0]] centroids[cent,:] = mean(ptsInClust, axis=0)return centroids, clusterAssmentK-Means 的评价标准
k-means算法因为手动选取k值和初始化随机质心的缘故,每一次的结果不会完全一样,而且由于手动选取k值,我们需要知道我们选取的k值是否合理,聚类效果好不好,那么如何来评价某一次的聚类效果呢?也许将它们画在图上直接观察是最好的办法,但现实是,我们的数据不会仅仅只有两个特征,一般来说都有十几个特征,而观察十几维的空间对我们来说是一个无法完成的任务。因此,我们需要一个公式来帮助我们判断聚类的性能,这个公式就是SSE (Sum of Squared Error, 误差平方和 ),它其实就是每一个点到其簇内质心的距离的平方值的总和,这个数值对应kmeans函数中clusterAssment矩阵的第一列之和。 SSE值越小表示数据点越接近于它们的质心,聚类效果也越好。 因为对误差取了平方,因此更加重视那些远离中心的点。一种肯定可以降低SSE值的方法是增加簇的个数,但这违背了聚类的目标。聚类的目标是在保持簇数目不变的情况下提高簇的质量。
相关文章:

K-Means(K-均值)聚类算法理论和实战
目录 K-Means 算法 K-Means 术语 K 值如何确定 K-Means 场景 美国总统大选摇争取摆选民 电商平台用户分层 给亚洲球队做聚类 编辑 其他场景 K-Means 工作流程 K-Means 开发流程 K-Means的底层代码实现 K-Means 的评价标准 K-Means 算法 对于 n 个样本点来说&am…...

Python-pyqt不同窗口数据传输【使用静态函数】
文章目录 前言程序1:caogao1.py输入数据界面程序2:caogao2.py接收数据界面 程序3 :将输入数据界面和接收数据界面组合成一个总界面讲解 总结 前言 在编写pyqt 页面时有时候需要不同页面进行数据传输。本文讲解静态函数方法。直接看示例。 程…...
百度垂类离线计算系统发展历程
作者 | 弘远君 导读 本文以百度垂类离线计算系统的演进方向为主线,详细描述搜索垂类离线计算系统发展过程中遇到的问题,以及对应的解决方案。架构演进过程中一直奉行“没有最好的架构,只有最合适的架构”的宗旨,面对不同阶段遇到的…...

ubuntu 安装 指定版本:nodejs
通过 PPA 安装指定或最新版本的 nodejs 那么就需要使用 nodesource 来安装指定版本的 nodejs 了。其需要下载一个脚本,运行此脚本会在 ubuntu 里添加一个 nodejs 源,然后用 apt 就可以下载指定的 nodejs 了。 PPA 的全称为 personal package archive 。要…...

16.CSS菜单悬停特效
效果 源码 <!DOCTYPE html> <html> <head> <title>Creative Menu Item Hover Effects</title> <link rel="stylesheet" type="text/css" href="style.css"> </head> <body><section><…...

恒运资本:市盈率怎么算?
市盈率(P/E ratio)是判别一家公司股票价格合理性的一个重要目标,也是投资者评估公司股票投资价值的重要参阅目标。市盈率越高,表明相对于公司的收益来说,该公司的股票定价越高。市盈率越低,则表明该股票被低…...

Docker运维中常见错误以及解决方法汇总1
1.报错如下: Another app is currently holding the yum lock; waiting for it to exit... 另一个应用程序是:PackageKit 原因:另一个APP正在锁定yum,等待其退出! 解决:执行指令 rm -f /var/run/yum.pid 2.CentOS7设置静态的IP且可以上网...

Maven - 使用maven-release-plugin规范化版本发布
文章目录 Maven Release plugin – IntroductionMaven Release plugin – Plugin DocumentationMaven Release plugin – Usage实战案例 Maven Release plugin – Introduction Maven Release Plugin(Maven 发布插件)是一个用于帮助在Maven项目中执行版…...
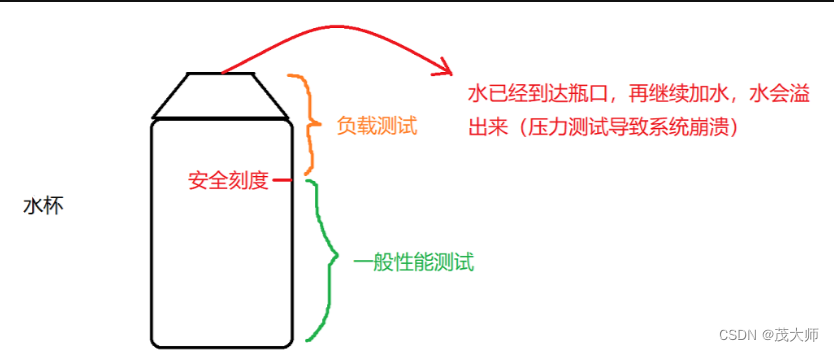
2023.8.29 关于性能测试
目录 什么是性能测试? 性能测试常见术语及其性能测试衡量指标 并发 用户数 响应时间 事务 点击率 吞吐量 思考时间 资源利用率 性能测试分类 基准性能测试 负载性能测试 压力性能测试 可靠性性能测试 性能测试执行流程 什么是性能测试? 性…...
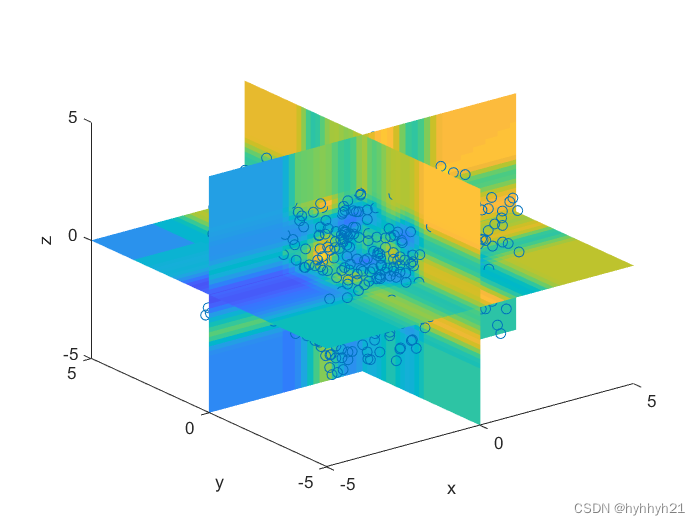
基于MATLAB的径向基函数插值(RBF插值)(一维、二维、三维)
基于MATLAB的径向基函数插值(RBF插值)(一维、二维、三维) 0 前言1 RBF思路2 1维RBF函数2.1 参数说明2.1.1 核函数选择2.1.2 作用半径2.1.3 多项式拟合2.1.4 误差项(光滑项) 3 2维RBF函数4 3维RBF函数 惯例声…...

flume拦截器
flume拦截器代码 1.依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apach…...

vue、elementui控制前一级选择后,后一级才会有数据
<el-form-item label"废物类型:"><el-select clearable v-model"queryForm.hswCateType" placeholder"请选择" change"industryCategoryChange" focus"industryCategoryFocus"><el-option v-for&…...
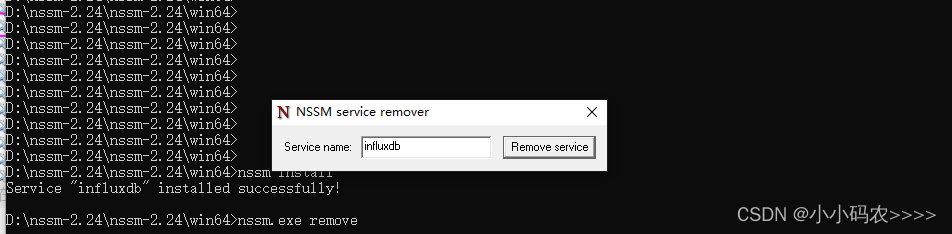
亲测influxdb安装为window后台服务
InfluxDB 安装 64bit:https://dl.influxdata.com/influxdb/releases/influxdb-1.7.4_windows_amd64.zip 解压安装包 修改配置文件 [meta]# Where the metadata/raft database is storeddir "D:/influxdb/meta"...[data]# The directory where the TSM…...
)
【LeetCode - 每日一题】823. 带因子的二叉树 (2023.08.29)
823. 带因子的二叉树 题意 元素都大于1,元素不重复。计数满足要求的二叉树(每个非叶结点的值应等于它的两个子结点的值的乘积)的数量。元素可以重复使用。 代码 自上而下动态规划。 所有元素大于1,所以不会有 自己自己自己 的…...

flutter 上传图片并裁剪
1.首先在pubspec.yaml文件中新增依赖pub.dev image_picker: ^0.8.75 image_cropper: ^4.0.1 2.在Android的AndroidManifest.xml文件里面添加权限 <activityandroid:name"com.yalantis.ucrop.UCropActivity"android:screenOrientation"portrait"andro…...
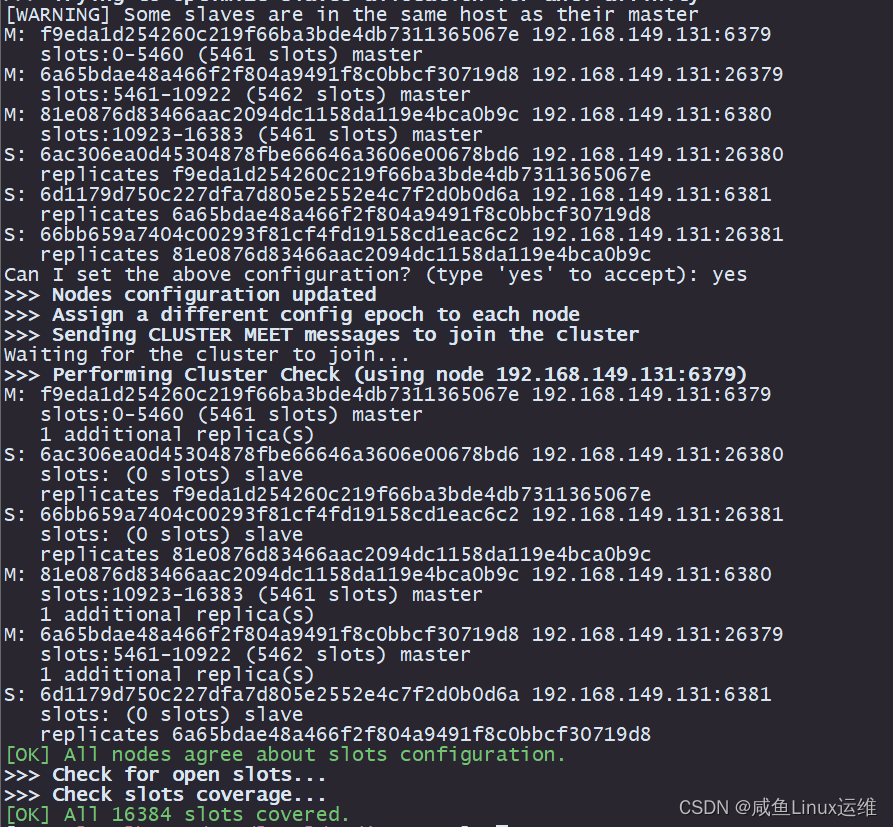
一台服务器上部署 Redis 伪集群
哈喽大家好,我是咸鱼 今天这篇文章介绍如何在一台服务器(以 CentOS 7.9 为例)上通过 redis-trib.rb 工具搭建 Redis cluster (三主三从) redis-trib.rb 是一个基于 Ruby 编写的脚本,其功能涵盖了创建、管…...

ealtek高清晰音频管理器(realtek高清晰音频管理器怎么设置win10)
本文为大家介绍realtek高清晰音频管理器(realtek高清晰音频管理器怎么设置win10),下面和小编一起看看详细内容吧。 我们都使用电脑来听音乐、看电影或者进行其他操作,但是如果我们觉得电脑产生的音效不够立体,我们就会想要去Realtek来设置音…...

微信小程序 scroll-view 组件的 bindscroll 不触发不生效
使用微信小程序基础组件中的scroll-view,但是滑动的时候 bindscroll 一直不生效。 <view class"container log-list"><scroll-view scroll-y style"height:100%;white-space:nowrap;" scroll-into-view"{{toView}}" enable…...

datax 删除分区数据,再写入MySQL脚本
#! /bin/bashDATAX_HOME/opt/module/datax#1、判断参数是否传入 if [ $# -lt 1 ] thenecho "必须传入all/表名..."exit fi #2、判断日期是否传入 [ "$2" ] && datestr$2 || datestr$(date -d -1 day %F)#DataX导出路径不允许存在空文件,…...

hyperf 十四 国际化
一 安装 composer require hyperf/translation:v2.2.33 二 配置 1、设置语言文件 文件结构: /storage/languages/en/messages.php /storage/languages/zh_CH/messages.php // storage/languages/en/messages.php return [welcome > Welcome to our applicat…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

