Python之动态规划
序言
最近在学习python语言,语言有通用性,此文记录复习动态规划并练习python语言。
动态规划(Dynamic Programming)
动态规划是运筹学的一个分支,是求解决策过程最优化的过程。20世纪50年代初,美国数学家贝尔曼(R.Bellman)等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,从而创立了动态规划。动态规划的应用极其广泛,包括工程技术、经济、工业生产、军事以及自动化控制等领域,并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。
基本思想:将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。
斐波那契数列(Fibonacci sequence)
斐波那契数列,又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称“兔子数列”,其数值为:1、1、2、3、5、8、13、21、34……在数学上,这一数列以如下递推的方法定义:F(0)=1,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)。
先以斐波那契数列为例,了解动态规划。
def fibonacci(num):if num == 0:return 1if num == 1:return 1return fibonacci(num - 1) + fibonacci(num - 2)if __name__ == "__main__":print(fibonacci(10))
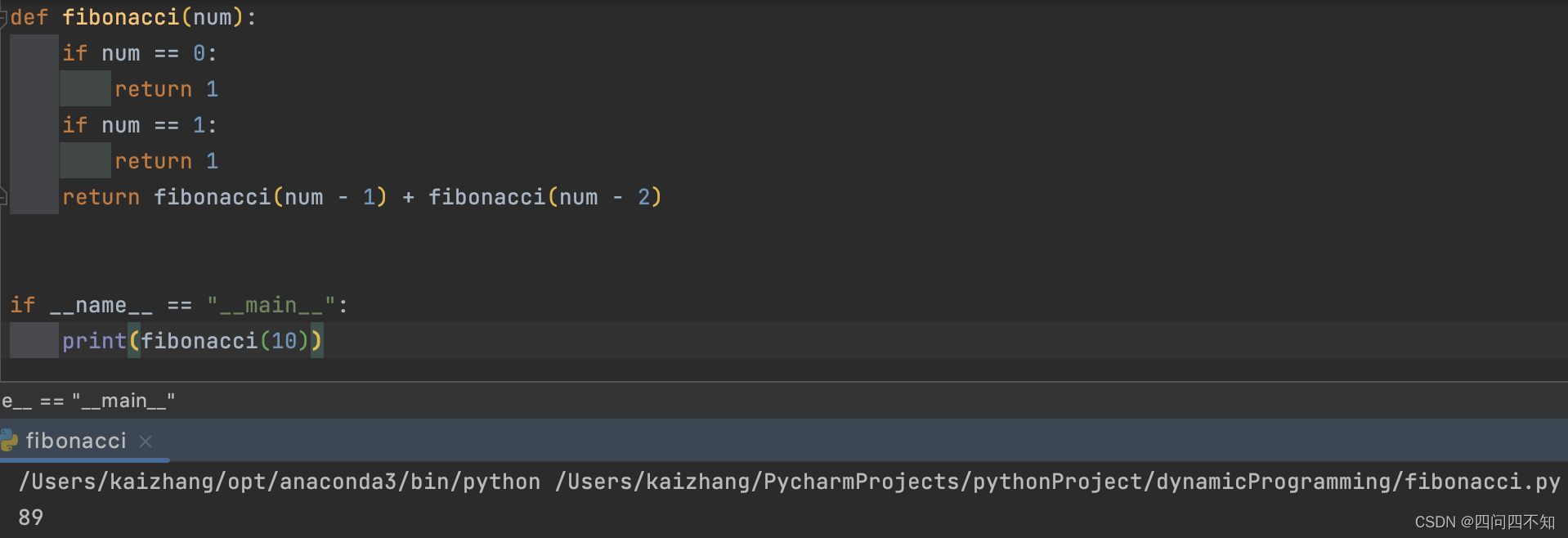
上述是以递归的方式实现的,然而递归方式存在以下几个缺点:
- 1)递归调用,占用空间大;
- 2)递归太深,容易发生栈溢出;
- 3)可能存在大量重复计算;
| 结果 | (n-1)项 | (n-2)项 |
|---|---|---|
| f(n) | f(n-1) | f(n-2) |
| … | … | … |
| f(5) | f(4) | f(3) |
| f(4) | f(3) | f(2) |
| f(3) | f(2) | f(1) |
| f(2) | f(1) | f(0) |
以上述表格为例,可以看到在求下一个递归结果时,计算了之前已经计算出来的结果,存在重复计算项。
如果采用动态规划的方式,那么可以节省计算,采用数组暂存之前已经计算出来的结果。如下,
def fibonacci_dp(num):# 定义一个数组暂存dp结果,数组初始值为-1dp = [-1] * (num + 1)dp[0] = 1dp[1] = 1for i in range(2, num + 1):dp[i] = dp[i - 1] + dp[i - 2]return dp[num]if __name__ == "__main__":print(fibonacci_dp(10))
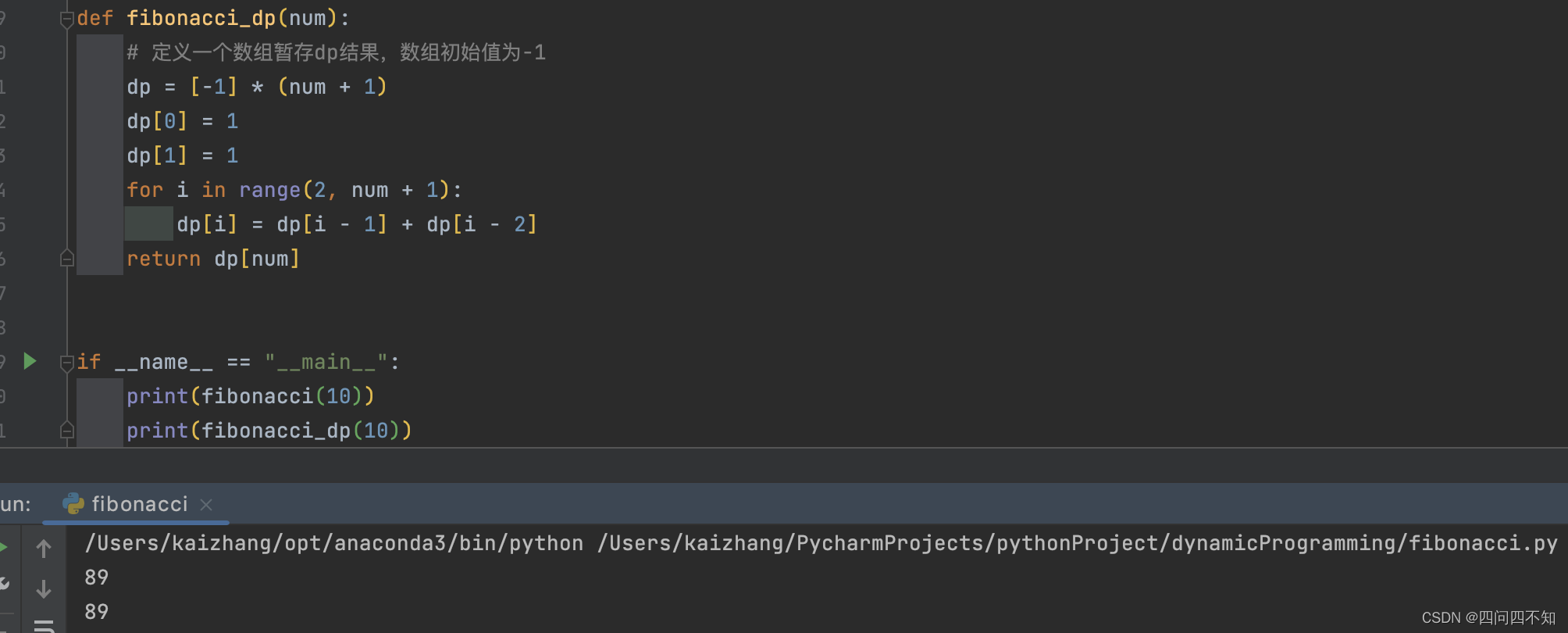
不同路径
上面的斐波那契数列是一维数组,较为简单,下面以二维数组为例。
题目描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?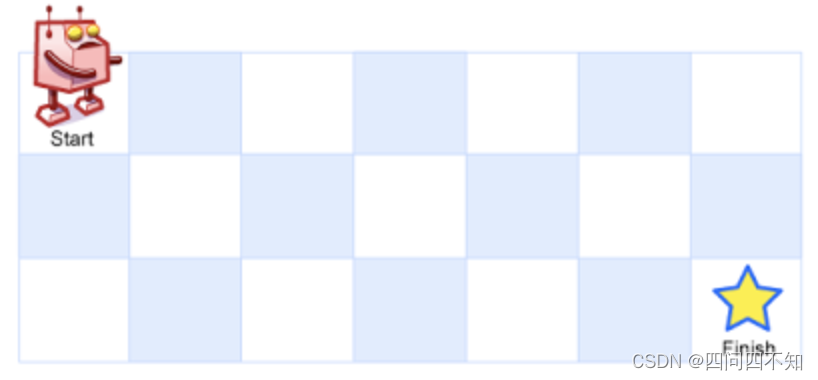
示例1: 输入:m = 3, n = 7 输出:28
示例2: 输入:m = 3, n = 2 输出:3
解释: 从左上角开始,总共有 3 条路径可以到达右下角。
1.向右 -> 向下 -> 向下
2.向下 -> 向下 -> 向右
3.向下 -> 向右 -> 向下
示例3:
输入:m = 7, n = 3 输出:28
示例4:
输入:m = 3, n = 3 输出:6
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9
python代码
class UniquePaths(object):def uniquePaths(self, m: int, n: int) -> int:""":type m: int:type n: int:rtype: int"""# 初始化一个二维数组dp = [[0] * n for _ in range(m)]for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i - 1][j] + dp[i][j - 1]return dp[m - 1][n - 1]if __name__ == "__main__":demo = UniquePaths()print(demo.uniquePaths(7, 3))
最小路径和
题目描述
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:一个机器人每次只能向下或者向右移动一步。
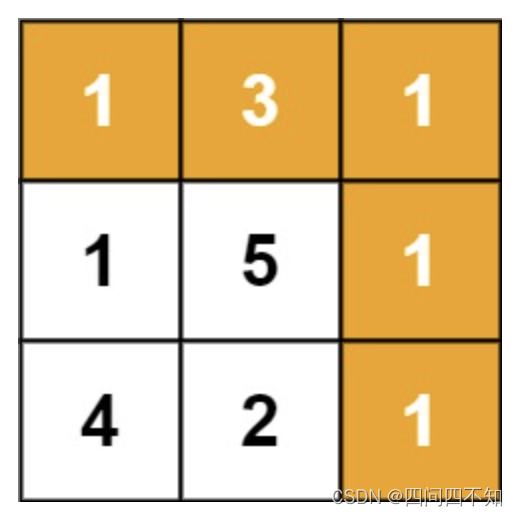
示例1:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
python代码
class MinPathSum(object):def minPathSum(self, grid):""":type grid: List[List[int]]:rtype: int"""row = len(grid)column = len(grid[0])# 定义dp[i][j]为到(i,j)处的最小路径和dp = [[0] * column for _ in range(row)]dp[0][0] = grid[0][0]# 第0行j列for j in range(1, column):dp[0][j] = dp[0][j - 1] + grid[0][j]# 第i行0列for i in range(1, row):dp[i][0] = dp[i - 1][0] + grid[i][0]# 非第0行或第0列for i in range(1, row):for j in range(1, column):dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]return dp[row - 1][column - 1]if __name__ == "__main__":demo = MinPathSum()grid = [[1, 3, 1], [1, 5, 1], [4, 2, 1]]print(demo.minPathSum(grid))

零钱兑换
题目描述
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
提示:
1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104
python代码
class CoinChange(object):def coinChange(self, coins: list[int], amount: int) -> int:""":type coins: List[int]:type amount: int:rtype: int"""# 状态转移方程dp(i) = min(dp(i-Cj)) + 1,Cj为货币面值"""i<0 忽略i==0 dp[0] = 0i==1 dp[1] = min(dp[1-1], dp[1-2], dp[1-5]) + 1 = 1i==2 dp[2] = min(dp[2-1], dp[2-2], dp[2-5]) + 1 = 1i==3 dp[3] = min(dp[3-1], dp[3-2], dp[3-5]) + 1 = 2i==4 dp[4] = min(dp[4-1], dp[4-2], dp[4-5]) + 1 = 2... ..."""dp = [0] * (amount + 1)dp[0] = 0for i in range(1, amount + 1):mini = int(1e9)for coin in coins:if i >= coin:res = dp[i - coin]if 0 <= res < mini:mini = resdp[i] = mini + 1 if mini < int(1e9) else -1if amount < 1:return 0return dp[amount]if __name__ == "__main__":demo = CoinChange()coins = [1, 2, 5]amount = 11print(demo.coinChange(coins, amount))
相关文章:

Python之动态规划
序言 最近在学习python语言,语言有通用性,此文记录复习动态规划并练习python语言。 动态规划(Dynamic Programming) 动态规划是运筹学的一个分支,是求解决策过程最优化的过程。20世纪50年代初,美国数学家…...

[ES]二基础 |
一、索引库操作 1、mapping属性 mapping是对索引库中文档的约束,常见的mapping属性包括: 1)type:字段数据类型,常见的简单类型有: ①字符串:text(可分词的文本)、keyword(精确值,…...

vscode vue3自定义自动补全
敲代码多了,发现重发动作很多,于是还是定义自动补全代码吧——懒是第一生产力! 1,Ctrl Shift P打开快捷命令行:找到下面这个 2,然后找到ts: 里面给了demo照着写就行 // "Print to conso…...

Spring Cloud + Spring Boot 项目搭建结构层次示例讲解
Spring Cloud Spring Boot 项目搭建结构层次示例讲解 Spring Cloud 项目搭建结构层次示例Spring Cloud示例: Spring Boot 项目搭建结构层次讲解Spring Boot 项目通常按照一种常见的架构模式组织,可以分为以下几个主要层次:当构建一个 Spring…...
使用cgroup工具对服务器某些/全部用户进行计算资源限制
使用cgroup工具对服务器某些/全部用户进行计算资源限制 主要介绍,如何对指定/所有用户进行资源限定(这里主要介绍cpu和内存占用限制),防止某些用户大量占用服务器计算资源,影响和挤占他人正常使用服务器。 安装cgrou…...
C#获取DataTable的前N行数据然后按指定字段排序
获取DataTable的前N行数据然后按指定字段排序 可以使用以下三种代码: 第一种:使用Linq DataTable dtLast dataTable.AsEnumerable().Take(count).OrderBy(dataRow > Convert.ToInt32(dataRow["Sequence"])).CopyToDataTable(); 第二种…...

Swift 中的动态成员查找
文章目录 前言基础介绍基础示例1. 定义一个动态成员访问类:2. 访问嵌套动态成员: 使用 KeyPath 的编译时安全性KeyPath 用法示例KeyPath 进阶使用示例1. 动态访问属性:2. 结合可选属性和 KeyPath:3. 动态 KeyPath 和字典ÿ…...

leetcode做题笔记102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 思路一:递归 int** levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes){int** ans(int**)mal…...
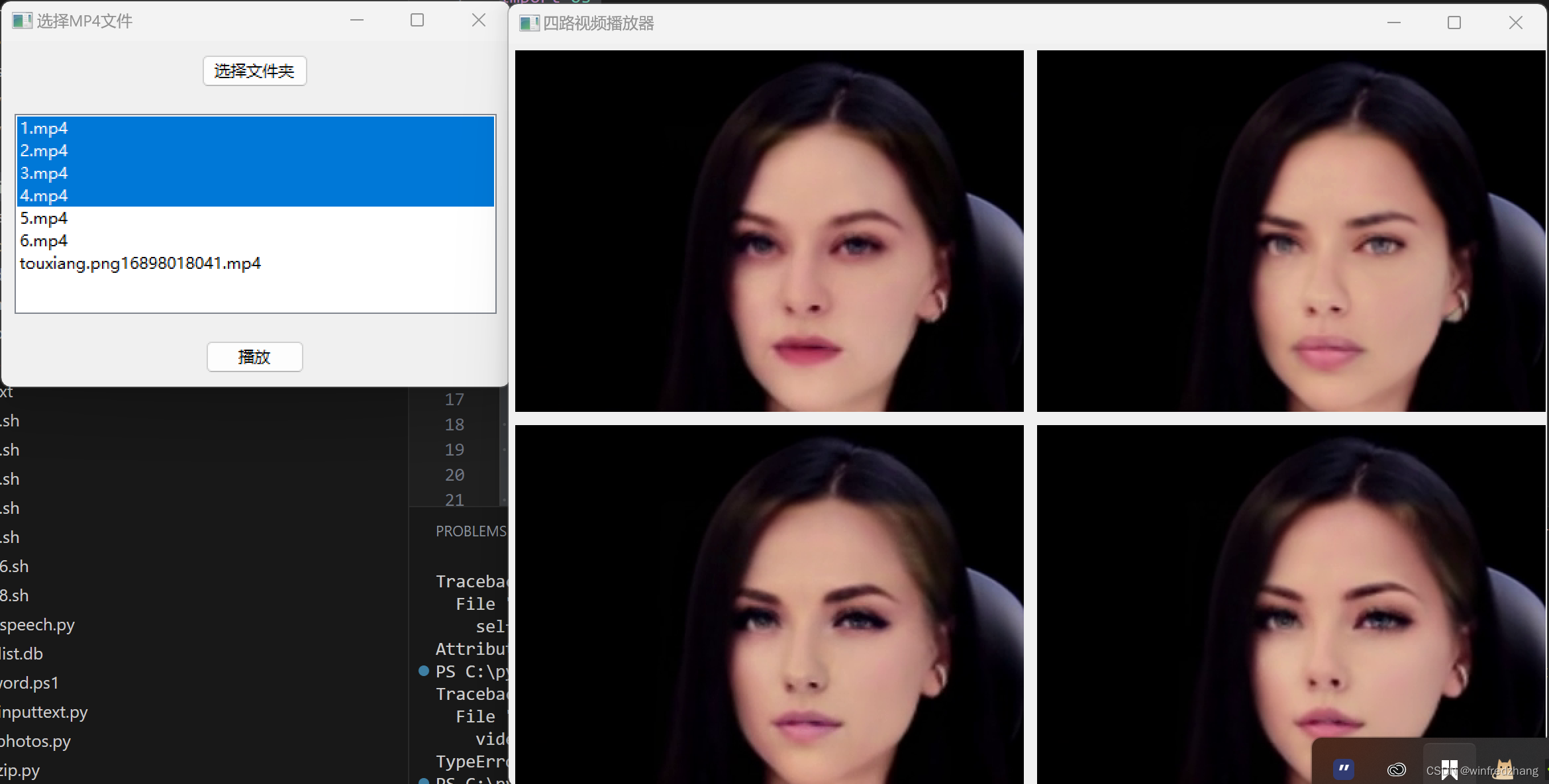
python编写四画面同时播放swap视频
当代技术让我们能够创建各种有趣和实用的应用程序。在本篇博客中,我们将探索一个基于wxPython和OpenCV的四路视频播放器应用程序。这个应用程序可以同时播放四个视频文件,并将它们显示在一个GUI界面中。 C:\pythoncode\new\smetimeplaymp4.py 准备工作…...

用XSIBackup为VMware ESXi打造完美备份方案
文章目录 VMware ESXi 备份方案引言XSIBackup安装步骤1. XSIBackup软件安装2. SSH连接3. 定位到xsibackup目录4. 修改文件权限5. 安装cron查看crontab列表6. 配置备份任务结论VMware ESXi 备份方案 引言 数据就像是我们的生命线,一旦丢失,可能会带来无法挽回的损失。对于那…...

React 项目中引入msal验证以及部分报错处理
功能实现 如何在React 项目中引入msal身份验证, 微软在官网有提供文档支持,文档包含示例和具体使用的教程,地址如下: https://learn.microsoft.com/zh-cn/azure/active-directory/develop/tutorial-v2-nodejs-webapp-msal 照着文…...

Unity3D 2021 使用 SharpZipLib 遇到的安卓打包 I18N 相关问题
在 Unity3D 中,使用 ICSharpCode.SharpZipLib.dll 来做压缩和解压缩,但打包安卓后遇到问题,原因是字符编码程序集被裁减掉了导致。 根据网上搜索,将 UnityEditor 对应目录下的 I18N开头的,比如 I18N.CJK.dll 等系列文…...
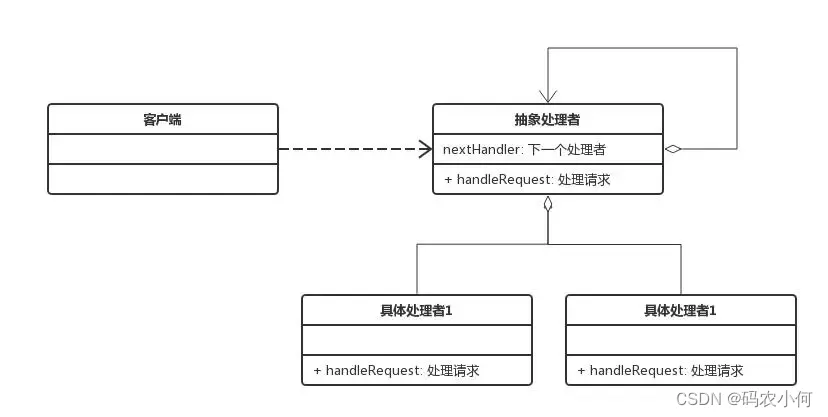
软件工程(十五) 行为型设计模式(一)
1、责任链模式 简要说明 通过多个对象处理的请求,减少请求的发送者与接收者之间的耦合。将接受对象链接起来,在链中传递请求,直到有一个对象处理这个请求。 速记关键字 传递职责 类图如下 由类图可以比较容易的看出来,其实就是自己关联自己,形成了一个链,并且自己有…...

【校招VIP】前端算法考点之快慢指针题型
考点介绍: 链表是校招面试里手撕代码出现频度比较高的题型,三线和中小厂会考察简单的链表反转,大厂会进一步考察复杂度和双指针问题,比如中间元素、是否存在环等。 『前端算法考点之快慢指针题型』相关题目及解析内容可点击文章末…...
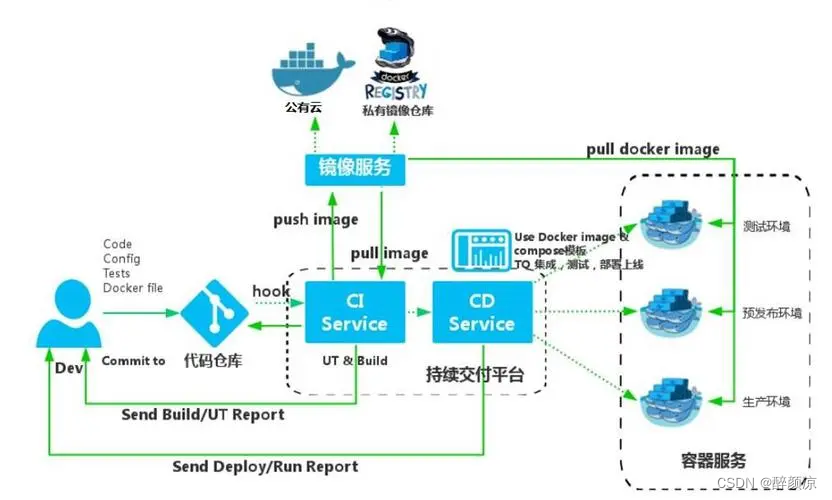
Docker基础入门:容器数据卷与Dockerfile构建镜像(发布)
Docker基础入门:容器数据卷与Dockerfile构建镜像(发布) 一、docker容器数据卷1.1、使用docker容器数据卷1.2、具名挂载、匿名挂载1.3、如何确定是具名挂载还是匿名挂载 二、使用dockerfile2.1 初识Dockerfile2.2 Dockerfile构建过程2.3 Docke…...
从零开始搭建一台NAS服务器(Linux虚拟机))
部署问题集合(二十一)从零开始搭建一台NAS服务器(Linux虚拟机)
前言 因工作需要,需要从零通过虚拟机搭建一台NAS服务器,以此记录下来 步骤 1、创建虚拟机 通过VMWare创建一台新虚拟机,虚拟机内存和磁盘自定义,不过建议尽量大一点 2、服务器端配置 查看是否安装有NFS服务:rpm …...
Git小白入门——了解分布式版本管理和安装
Git是什么? Git是目前世界上最先进的分布式版本控制系统(没有之一) 什么是版本控制系统? 程序员开发过程中,对于每次开发对各种文件的修改、增加、删除,达到预期阶段的一个快照就叫做一个版本。 如果有一…...

芯科科技宣布推出下一代暨第三代无线开发平台,打造更智能、更高效的物联网
第三代平台中的人工智能/机器学习引擎可将性能提升100倍以上 Simplicity Studio 6软件开发工具包通过新的开发环境将开发人员带向第三代平台 中国,北京 - 2023年8月22日 – 致力于以安全、智能无线连接技术,建立更互联世界的全球领导厂商Silicon Labs&…...

无涯教程-Android - Intents/Filters
Android Intent 是要执行的操作的抽象描述。它可以与 startActivity 一起启动Activity,将 broadcastIntent 发送给任何BroadcastReceiver组件,并与 startService(Intent)或 bindService(Intent,ServiceConnection,int)与后台服务进…...
NFTScan 正式上线 Base NFTScan 浏览器和 NFT API 数据服务
2023 年 8 月 24 号,NFTScan 团队正式对外发布了 Base NFTScan 基础设施,将为 Base 生态的 NFT 开发者和用户提供简洁高效的 NFT 数据搜索查询服务。NFTScan 作为全球领先的 NFT 数据基础设施服务商,Base 是继 Bitcoin、Ethereum、BNBChain、…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
