LeetCode 面试题 01.08. 零矩阵
文章目录
- 一、题目
- 二、C# 题解
一、题目
编写一种算法,若M × N矩阵中某个元素为0,则将其所在的行与列清零。
点击此处跳转题目。
示例 1:
输入:
[
[1,1,1],
[1,0,1],
[1,1,1]
]
输出:
[
[1,0,1],
[0,0,0],
[1,0,1]
]
示例 2:
输入:
[
[0,1,2,0],
[3,4,5,2],
[1,3,1,5]
]
输出:
[
[0,0,0,0],
[0,4,5,0],
[0,3,1,0]
]
二、C# 题解
此题有很多方法解,无外乎都是记录需要清零的行与列,这种写法太无聊了。这里提出一种递归的方式,只需要遍历矩阵一次即可。当遇到 0 时,使用 set0 变量记录该位置,遍历完成后,重置所有 set0。
public class Solution {public void SetZeroes(int[][] matrix) {BFS(ref matrix, 0, 0); // 广度优先遍历}public void BFS(ref int[][] matrix, int i, int j) {int m = matrix.Length, n = matrix[0].Length;if (i == m && j == 0) return; // 递归出口// 计算下一个位置int next_i = i, next_j = j + 1;if (next_j == n) {next_j = 0;next_i++;}bool set0 = matrix[i][j] == 0; // 记录当前状态,是否需要清零BFS(ref matrix, next_i, next_j); // 继续遍历// 最后执行清零if (set0) {for (int p = 0; p < n; p++) matrix[i][p] = 0;for (int q = 0; q < m; q++) matrix[q][j] = 0;}}
}
- 时间复杂度: O ( m × n ) O(m\times n) O(m×n)。
- 空间复杂度:由矩阵中 0 出现的次数决定。
该方法依据元素记录,因此当矩阵中 0 出现次数过多时,会有重复操作,只适合处理稀疏 0 矩阵。
矩阵中 0 过于密集时,使用记录行列的方式会更好些,但可能需要更多的空间和遍历次数。
相关文章:

LeetCode 面试题 01.08. 零矩阵
文章目录 一、题目二、C# 题解 一、题目 编写一种算法,若M N矩阵中某个元素为0,则将其所在的行与列清零。 点击此处跳转题目。 示例 1: 输入: [ [1,1,1], [1,0,1], [1,1,1] ] 输出: [ [1,0,1], [0,0,0], [1,0,1] ] 示…...

Qt应用开发(基础篇)——进度条 QProgressBar
一、前言 QProgressBar类继承于QWidget,是一个提供了横向或者纵向进度条的小部件。 QProgressBar进度条一般用来显示用户某操作的进度,比如烧录、导入、导出、下发、上传、加载等这些需要耗时和分包的概念,让用户知道程序还在正常的执行中。 …...
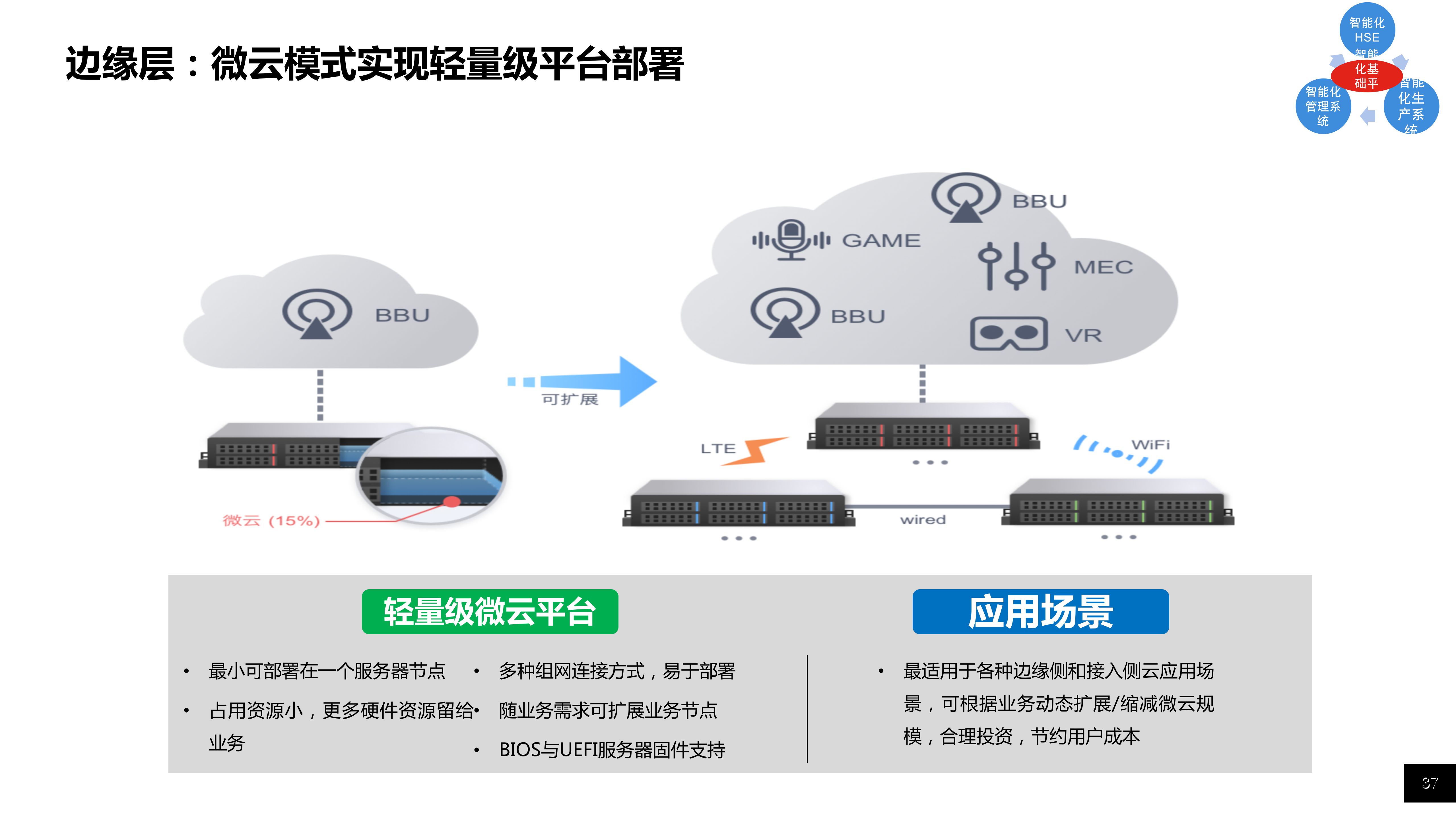
108页石油石化5G智慧炼化厂整体方案PPT
导读:原文《108页石油石化5G智慧炼化厂整体方案PPT》(获取来源见文尾),本文精选其中精华及架构部分,逻辑清晰、内容完整,为快速形成售前方案提供参考。以下是部分内容,...

Codeforces 1625E2 括号树 + BIT
题意 传送门 Codeforces 1625E2 Cats on the Upgrade (hard version) 题解 首先利用栈将原始字符串转换为合法的 RBS,不能匹配的括号设为 ‘.’。根据匹配的括号序列构造树,具体而言,遇到左括号,则新建节点向下递归,…...

PHP命令行CLI的使用
PHP命令行界面 PHP命令行界面(CLI)是一种使用命令行(终端)来运行PHP脚本的方式,与在Web服务器环境下运行PHP不同。CLI提供了一种与操作系统交互的方式,能够在命令行中直接执行PHP代码。 以下是一些与PHP命…...

近期嵌软线下笔试题记录
1、以下代码的输出结果是? #include <stdio.h> #include <string.h>int main() {int a,b,c,d;a 10;b a; //a先赋值给b,然后自增1c a; //a自增1后赋值给cd 10*a; //先进行运算然后a自增1printf("b,c,d:%d…...
基于MYSQL的主从同步和读写分离
目录 一.完成MySQL主从同步(一主两从) 1.主库配置 2.建立同步账号 3.锁表设置只读 4.备份数据库数据 5.主库备份数据上传到从库 6.从库上还原备份 7.解锁 8.从库上设定主从同步 9.启动从库同步开关 10.检查状态 二.基于MySQL一主两从配置&…...

java八股文面试[多线程]——合适的线程数是多少
知识来源: 【并发与线程】 合适的线程数量是多少?CPU 核心数和线程数的关系?_哔哩哔哩_bilibili 【2023年面试】程序开多少线程合适_哔哩哔哩_bilibili...

Linux系统下vim常用命令
一、基础命令: v:可视模式 i:插入模式 esc:命令模式下 :q :退出 :wq :保存并退出 ZZ:保存并退出 :q! :不保存并强制退出二、在Esc下: dd : 删除当前行 yy:复制当前行 p:复制已粘贴的文本 u:撤销上一步 U:…...

【2023】LeetCode HOT 100——链表
目录 1. 相交链表1.1 C++实现1.2 Python实现1.3 时空分析2. 反转链表2.1 C++实现2.2 Python实现2.3 时空分析3. 回文链表3.1 C++实现3.2 Python实现3.3 时空分析4. 环形链表4.1 C++实现4.2 Python实现4.3 时空分析5. 环形链表 II5.1 C++实现5.2 Python实现...
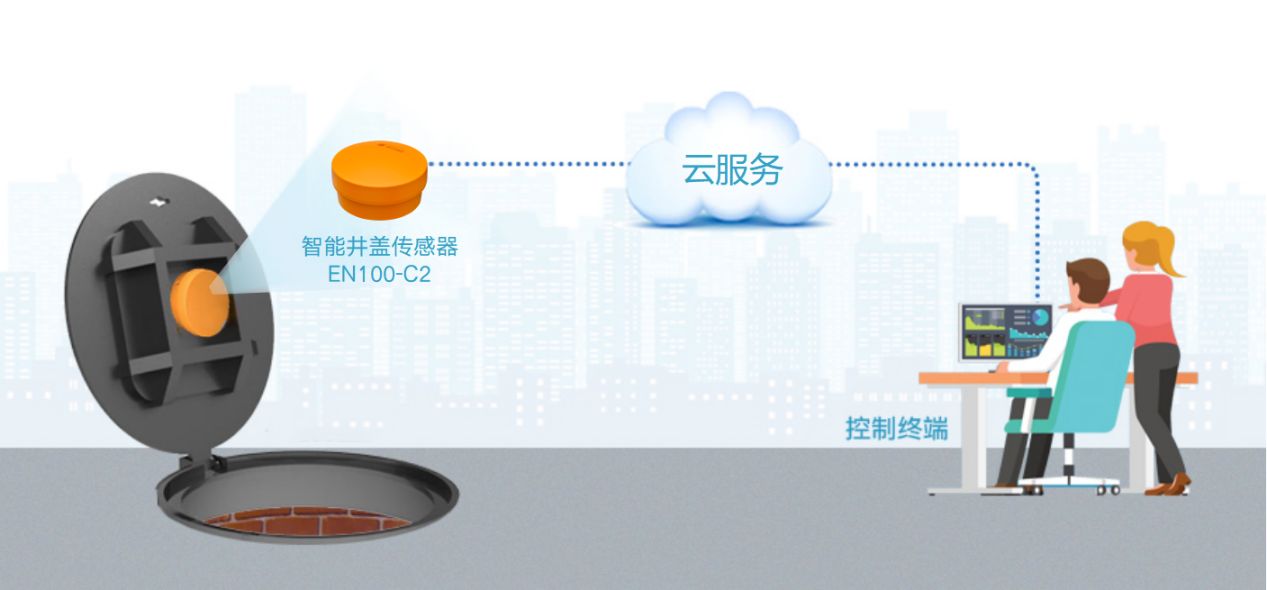
智能井盖传感器,物联网智能井盖系统
随着城市人口的不断增加和城市化进程的不断推进,城市基础设施的安全和可靠性变得愈发重要,城市窨井盖作为城市基础设施重要组成部分之一,其安全性事关城市安全有序运行和居民生产生活安全保障。 近年来,各地都在加强城市窨井盖治理…...

C语言三子棋解析
目录(标2的是我自己写的一堆问题不知道怎么改) 开始菜单1打印棋盘1玩家下棋1电脑下棋1判断输赢1开始菜单2打印棋盘2选择先后2玩家下棋2电脑下棋2判断输赢2完整代码文件else.h文件else.c文件test.c 开始菜单1 void menu()//打印菜单 {printf("*****…...
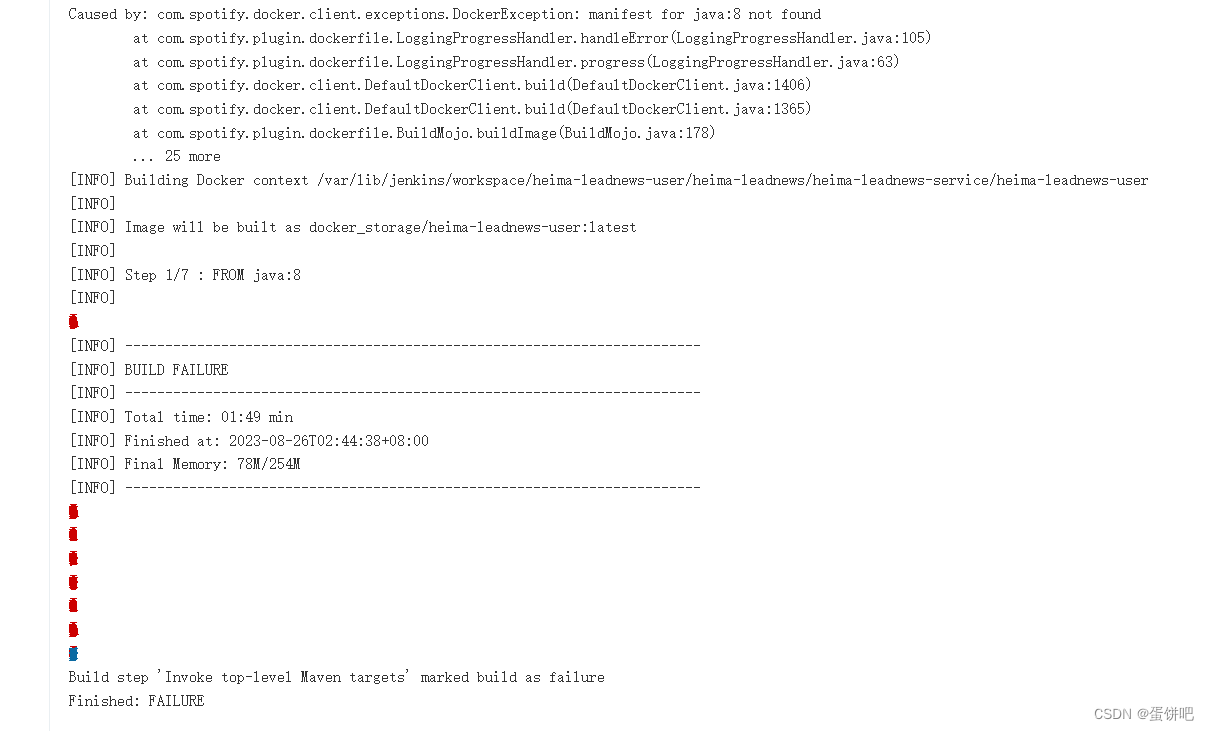
【Jenkins打包服务,Dockerfile报错:manifest for java : 8 not fourd】
1、问题描述 Jenkins打包服务运行dockerfile里的FROM java:8报错manifest for java : 8 not fourd Caused by: com.spotify. docker.client.exceptions.DockerException: manifest for java:8 not found2、解决方法 在网上查找许多方法后得出这是由于Docker官方已经弃用java…...
读SQL学习指南(第3版)笔记06_连接和集合
1. 连接 1.1. 笛卡儿积 1.1.1. 交叉连接(cross join) 1.1.2. 查询并没有指定两个数据表应该如何连接,数据库服务器就生成了笛卡儿积 1.1.2.1. 两个数据表的所有排列组合 1.1.3. 很少会用到(至少不会特意用到) 1.…...

C#学习,结构,面向对象,类
结构和类 结构是从过程化程序设计中保留下来的一种数据类型,类则是面向对象程序设计中最基本的、也是最重要的概念。 结构 结构是一种值类型,通常用来封装一组相关的变量,结构中可以包含构造函数、变量、字段、方法、属性、运算符、事件和…...

【PHP】文件操作
文章目录 文件编程的必要性目录操作其它目录操作递归遍历目录PHP5常见文件操作函数PHP4常见文件操作函数其他文件操作函数 文件编程的必要性 文件编程指利用PHP代码针对文件(文件夹)进行增删改查操作。 在实际开发项目中,会有很多内容&…...

科创板50ETF期权交易:详细规则、费用、保证金和开户攻略
科创板50ETF期权是指以科创板50ETF为标的资产的期权合约。科创板50ETF是由交易所推出的一种交易型开放式指数基金(ETF),旨在跟踪科创板50指数的表现,下文介绍科创板50ETF期权交易:详细规则、费用、保证金和开户攻略&am…...
怎么把图片放大并且清晰?有详细的方法步骤
怎么把图片放大并且清晰?数字图像处理中的图片放大是许多行业和领域中广泛应用的一项技术。常规的放大方法通过插值或复制像素的方式增加像素数,但这会导致失真和模糊。无损放大是一种特殊的放大方法,它可以通过数学算法来增加图片的尺寸&…...

C++ 构造函数、析构函数调用虚函数
C虚函数是通过虚表实现的,虚函数的地址记录在需表中,只对象完成构造完成后,虚函数的地址才最终确定。 构造函数中调用虚函数 基类先于派生类构造,所以构造时没法调用到派生类的虚函数,也就是说只能调用到自己&#x…...

工业状态监测如何选择合适的无线技术?
工业领域的状态监测在提高生产效率和产品质量方面起着关键作用。过去依赖于预防性维护和例行检查的方式已经不再能满足日益复杂的生产需求,随着工业物联网(IIoT)的兴起,设备状态监测逐渐成为一种关键策略,催生了预测性…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
